Lý thuyết đối xứng trụcHai điểm gọi là đối xứng với nhau qua đường thẳng d nếu d là đường trung trực của đoạn thẳng Quảng cáo
I. Các kiến thức cần nhớ 1. Đối xứng trục  Định nghĩa: Hai điểm $A,B$ gọi là đối xứng với nhau qua đường thẳng $d$ nếu $d$ là đường trung trực của đoạn thẳng nối hai điểm đó. 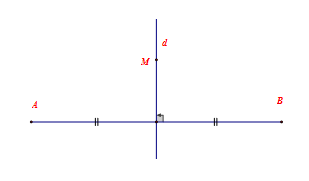 Quy ước: Nếu điểm $M$ nằm trên đường thẳng $d$ thì điểm đối xứng với $M$ qua đường thẳng $d$ cũng là điểm $M$ . 2. Hai hình đối xứng qua một đường thẳng Định nghĩa: Hai hình gọi là đối xứng với nhau qua đường thẳng $d$ nếu mỗi điểm thuộc hình này đối xứng với một điểm thuộc hình kia qua đường thẳng $d$ và ngược lại. Đường thẳng $d$ gọi là trục đối xứng của hai hình đó. 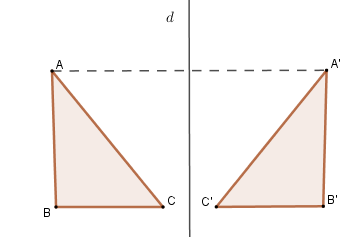 Chú ý: Nếu hai đoạn thẳng (góc, tam giác) đối xứng với nhau qua một đường thẳng thì chúng bằng nhau. 3. Hình có trục đối xứng Đường thẳng $d$ gọi là trục đối xứng của hình $H$ nếu điểm đối xứng với mỗi điểm thuộc hình $H$ qua đường thẳng $d$ cũng thuộc hình $H$ . Ta nói hình $H$ có trục đối xứng. 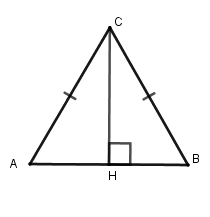 Định lý: Đường thẳng đi qua trung điểm hai đáy của hình thang cân là trục đối xứng của hình thang cân đó. 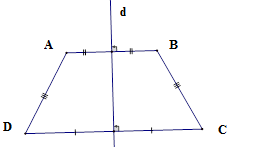 II. Các dạng toán thường gặp Dạng 1: Tính độ dài cạnh, chu vi tam giác, tứ giác Phương pháp: Sử dụng chú ý: “Nếu hai đoạn thẳng (góc, tam giác) đối xứng với nhau qua một đường thẳng thì chúng bằng nhau.” Dạng 2: Chứng minh (nhận biết) các hình đối xứng nhau qua một đường thẳng. Phương pháp: Ta sử dụng định nghĩa: “ Hai điểm $A,B$ gọi là đối xứng với nhau qua đường thẳng $d$ nếu $d$ là đường trung trực của đoạn thẳng nối hai điểm đó.”  Chia sẻ Bình luận
Quảng cáo
Tham Gia Group Dành Cho 2K11 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
|
