Lý thuyết con lắc lò xoPhương trình động lực học của dao động... Quảng cáo
I. Con lắc lò xo - Con lắc lò xo gồm một vật nặng m gắn vào một đầu của lò xo có độ cứng k và có khối lượng không đáng kể. - Con lắc có một vị trí cân bằng mà khi ta thả vật ra, vật sẽ đứng yên mãi. Nếu kéo vật ra khỏi vị trí cân bằng buông ra vật sẽ dao động quanh vị trí cân bằng giữa hai biên. Video mô phỏng chuyển động của con lắc lò xo II. Khảo sát dao động của con lắc lò xo về mặt động lực học - Xét vật ở li độ x, lò xo giãn một đoạn \(\Delta l = x\), lực đàn hồi của lò xo \(F = - k\Delta l\) Phương trình dao động của con lắc lò xo về mặt động lực học là: \(F = ma = - k{\rm{x}}\) hay \(a = - \frac{k}{m}x\) Trong đó: F: là lực tác dụng lên m (N) x: là li độ của vật (m) k: độ cứng của lò xo (N/m) dấu (-) chỉ ra rằng lực \(\overrightarrow F \) luôn hướng về vị trí cân bằng. - Đặt \({\omega ^2} = \frac{k}{m} \Rightarrow a + {\omega ^2}x = 0\) - Dao động của con lắc lò xo là dao động điều hòa: + Tần số góc: \(\omega = \sqrt {\frac{k}{m}} \) + Chu kì: \(T = 2\pi \sqrt {\frac{m}{k}} \) - Lực luôn hướng về vị trí cân bằng gọi là lực kéo về. Nó có độ lớn tỉ lệ với li độ và là lực gây ra gia tốc cho vật dao động điều hòa. * Tổng hợp các dạng con lắc lò xo
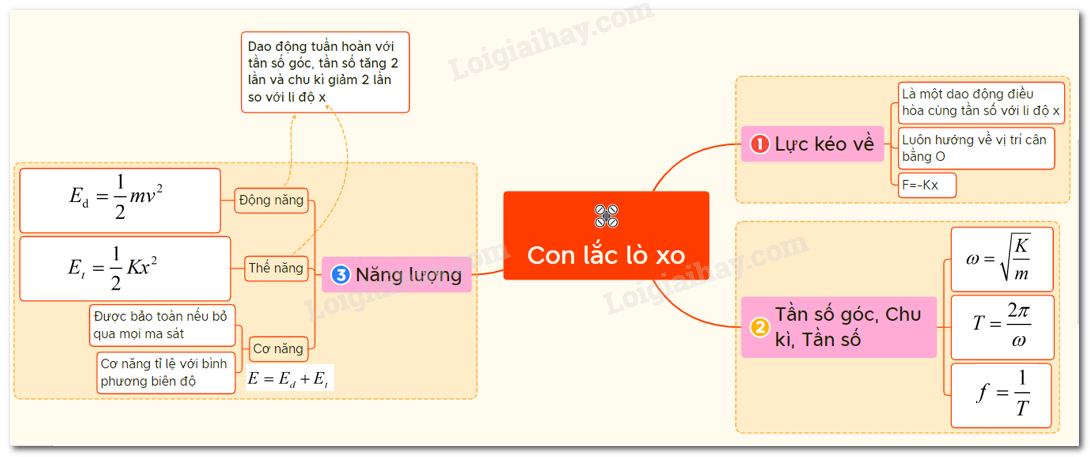
III. Khảo sát dao động của con lắc lò xo về mặt năng lượng 1. Động năng của con lắc lò xo - Động năng của con lắc lò xo là động năng của vật m: \({W_d} = \frac{1}{2}m{v^2}\left( J \right)\)\( = \frac{1}{4}K{A^2} - \frac{1}{4}K{A^2}\cos (2\omega t + 2\varphi )\) 2. Thế năng của con lắc lò xo \({{\rm{W}}_t} = \frac{1}{2}k{{\rm{x}}^2}\left( J \right)\)\( = \frac{1}{4}K{A^2} + \frac{1}{4}K{A^2}\cos (2\omega t + 2\varphi )\) 3. Cơ năng của con lắc lò xo. Sự bảo toàn cơ năng - Cơ năng của con lắc: \({\rm{W}} = \frac{1}{2}m{v^2} + \frac{1}{2}k{{\rm{x}}^2}\left( J \right)\) - Khi không có ma sát thì cơ năng của con lắc được bảo toàn. Nó chỉ biến đổi từ thế năng sang động năng và ngược lại. \({\rm{W}} = \frac{1}{2}k{A^2} = \frac{1}{2}m{\omega ^2}{A^2} = const\) *Nhận xét: - Động năng và thế năng của con lắc lò xo biến thiên điều hòa cùng tần số góc \(2\omega \), tần số \(2f\), chu kì \(\frac{T}{2}\). - Thời gian liên tiếp giữa hai lần động năng bằng thế năng là \(\frac{T}{4}\) - Cơ năng của con lắc lò xo luôn được bảo toàn và tỉ lệ với bình phương biên độ dao động. Sơ đồ tư duy về con lắc lò xo
|





















Danh sách bình luận