Trắc nghiệm Tính độ dài đoạn thẳng và tỉ số hai đoạn thẳng bằng cách sử dụng tính chất đường phân giác Toán 8 có đáp án
Trắc nghiệm Tính độ dài đoạn thẳng và tỉ số hai đoạn thẳng bằng cách sử dụng tính chất đường phân giác
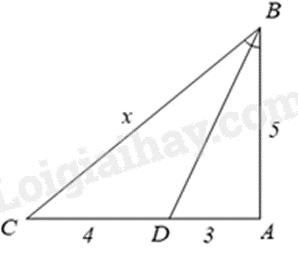
Cho tam giác \(ABC\) có \(BE\) là phân giác góc \(ABC\) (\(E \in AC\)). Cho \(AB = 6\,cm\), \(BC = x\,cm\), \(AE = 5\,cm\), \(EC = 3\,cm\). Giá trị của \(x\) là:
-
A
\(10\);
-
B
\(4\);
-
C
\(3,6\);
-
D
\(2,5\).
Cho tam giác \(OMN\) có \(OD\) là đường phân giác góc \(MON\) (\(D \in MN\)). Biết \(DN = 7\,cm\), \(ON = 9\,cm\). Tỉ số \(\frac{{OM}}{{MD}}\) là:
-
A
\( \frac{9}{7}\);
-
B
\( \frac{1}{7}\);
-
C
\( \frac{7}{9}\);
-
D
\( \frac{1}{9}\).
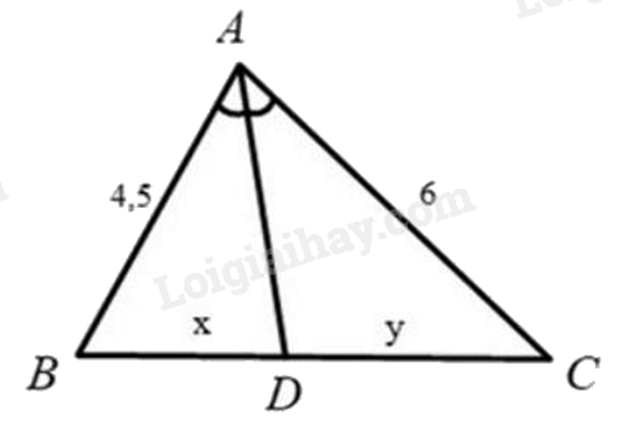
Cho tam giác \(ABC\) có \(CE\) là đường phân giác góc \(ACB\) (\(E \in AB\)). Biết \(AB = 8\,cm\), \(AC = 6\,cm\), \(BC = 10\,cm\), \(AE = x\,cm\), \(EB = y\,cm\). Giá trị của \(x\) và \(y\) lần lượt là:
-
A
\(5;\, 4\);
-
B
\(3;\, 7\);
-
C
\(5;\, 3\);
-
D
\(3;\, 5\).
Cho tam giác \(DEF\) có \(DI\) là đường phân giác của góc \(EDF\) (\(I \in EF\)). Biết \(DE = 5\,cm\), \(EF = 9\,cm\), \(DF = 8\,cm\). Tỉ số diện tích của hai tam giác \(DEI\) và \(DFI\) là:
-
A
\(\frac{5}{8}\);
-
B
\(\frac{5}{9}\);
-
C
\(\frac{8}{5}\);
-
D
\(\frac{9}{8}\);
Cho tam giác \(ABC\) có ba đường phân giác \(AD,\, BE,\, CF\) cắt nhau tại \(I\). Gọi \(G,\, H,\, K\) lần lượt là hình chiếu của \(I\) lên \(AB,\, AC,\, BC\). Biết \(GI = 12\,cm\). Độ dài \(IK\) là:
-
A
\(4\,cm\);
-
B
\(8\,cm\);
-
C
\(6\,cm\);
-
D
\(12\,cm\).
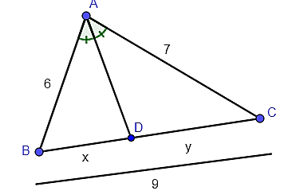
Cho hình vẽ dưới đây. Khi đó giá trị \(y - x\) là:
-
A
\( \frac{19}{3}\);
-
B
\( \frac{9}{13}\);
-
C
\( \frac{5}{13}\);
-
D
\( \frac{13}{19}\).
Cho tam giác \(ABC\) có chu vi là \(18\,cm\), các đường phân giác \(BD,\, CE\). Tính các cạnh của tam giác \(ABC\) biết \(\frac{{AD}}{{DC}} = \frac{1}{2};\,\frac{{AE}}{{EB}} = \frac{3}{4}\).
-
A
\(AB = 8\,cm,\, BC = 4\,cm,\, AC = 6\, cm\);
-
B
\(AB = 4\,cm,\, BC = 8\,cm,\, AC = 6\, cm\);
-
C
\(AB = 4\,cm,\, BC = 6\,cm,\, AC = 8\, cm\);
-
D
\(AB = 8\,cm,\, BC = 6\,cm,\, AC = 4\, cm\).
Cho tam giác ABC có BD là tia phân giác trong của góc B (\(D \in AC\)) thì
-
A
\(\frac{{AB}}{{BC}} = \frac{{DC}}{{BD}}\).
-
B
\(\frac{{AB}}{{BC}} = \frac{{DC}}{{AC}}\).
-
C
\(\frac{{AB}}{{BC}} = \frac{{DA}}{{DC}}\).
-
D
\(\frac{{AB}}{{BC}} = \frac{{DA}}{{AC}}\).
-
A
\(\frac{4}{3}\).
-
B
\(\frac{1}{3}\).
-
C
\(\frac{2}{3}\).
-
D
\(\frac{3}{4}\).
Cho tam giác ABC, đường phân giác AD (D \( \in \) BC). Biết AB = 2cm, AC = 3cm, BD = 1,6cm. Khi đó độ dài CD bằng
-
A
2,8cm.
-
B
1,8cm.
-
C
2,2cm.
-
D
2,4cm.
Cho \(\Delta ABC\) có \(AB = 4cm;AC = 9cm\). Gọi AD là tia phân giác của \(\widehat {BAC}\) . Tính tỉ số \(\frac{{CD}}{{BD}}\).
-
A
\(\frac{9}{4}\).
-
B
\(\frac{4}{9}\).
-
C
\(\frac{4}{5}\).
-
D
\(\frac{5}{4}\).
Cho \(\Delta ABC\), tia phân giác góc trong của góc A cắt BC tại D. Cho \(AB = 6\), \(AC = x,BD = 9\),\(BC = 21\). Tính kết quả đúng của độ dài cạnh x?
-
A
\(x = 14\).
-
B
\(x = 6\).
-
C
\(x = 12\).
-
D
\(x = 8\).
-
A
\(\frac{{20}}{3}\).
-
B
\(\frac{3}{{20}}\).
-
C
\(\frac{{15}}{4}\).
-
D
\(\frac{4}{{15}}\).
Cho tam giác ABC, AD là đường phân giác của \(\widehat {BAC}\left( {D \in BC} \right)\). Tỉ lệ thức nào sau đây đúng?
-
A
\(\frac{{AB}}{{BD}} = \frac{{AC}}{{BC}}\).
-
B
\(\frac{{AD}}{{AC}} = \frac{{BD}}{{DC}}\).
-
C
\(\frac{{DB}}{{AB}} = \frac{{DC}}{{AC}}\).
-
D
\(\frac{{DB}}{{DC}} = \frac{{BC}}{{AC}}\).
-
A
\(\frac{7}{{15}}\).
-
B
\(\frac{1}{7}\).
-
C
\(\frac{{15}}{7}\).
-
D
\(\frac{1}{{15}}\).