Trắc nghiệm Tính độ dài đoạn thẳng bằng cách sử dụng định lí Thales Toán 8 có đáp án
Trắc nghiệm Tính độ dài đoạn thẳng bằng cách sử dụng định lí Thales
Chọn câu trả lời đúng: Cho hình bên, biết \(ED \bot AB,AC \bot AB\), tìm \(x\):
-
A
\(x = 3\)
-
B
\(x = 2,5\)
-
C
\(x = 2\)
-
D
\(x = 4\)\(\)
-
A
12
-
B
21
-
C
14
-
D
15
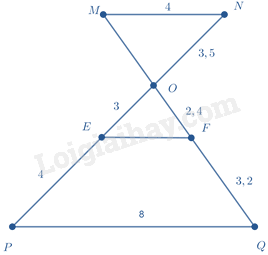
-
A
\(OM = 2,8\)
-
B
\(OM = 1,8\)
-
C
\(OM = 3,8\)
-
D
\(OM = 0,8\)
Cho tam giác \(ABC\) có \(AB = 12{\rm{ cm}}\) , điểm \(D\) thuộc cạnh \(AB\) sao cho \(AD = 8{\rm{ cm}}\) . Kẻ \(DE\) song song với \(BC\,\left( {E \in AC} \right)\) , kẻ \(EF\) song song với \(CD\,\left( {F \in AB} \right)\) . Tính độ dài \(AF\) .
-
A
2 cm
-
B
\(\frac{4}{3}\) cm
-
C
3 cm
-
D
\(\frac{{16}}{3}\) cm
Cho điểm \(M\) thuộc đoạn thẳng \(AB\) sao cho \(MA = 2MB\) . Vẽ về một phía của \(AB\) các tam giác đều \(AMC\) và \(MBD\) . Gọi \(E\) là giao điểm của \(AD\) và \(MC\) , \(F\) là giao điểm của \(BC\) và \(DM\) . Đặt \(MB = a\) . Tính \(ME,MF\) theo \(a\) .
-
A
\(ME = \frac{a}{2};MF = \frac{a}{3}\)
-
B
\(ME = MF = \frac{{2a}}{3}\)
-
C
\(ME = \frac{{2a}}{3};MF = \frac{a}{3}\)
-
D
\(ME = MF = \frac{a}{3}\)
Cho hình thang \(ABCD\left( {AB // CD} \right)\) có diện tích \(48\,{\rm{c}}{{\rm{m}}^2}\) , \(AB = 4\,{\rm{cm,}}\,CD = 8{\rm{cm}}\) . Gọi \(O\) là giao điểm của hai đường chéo. Tính diện tích tam giác \(COD\)
-
A
\(\frac{{64}}{3}{\rm{c}}{{\rm{m}}^2}\)
-
B
\({\rm{15c}}{{\rm{m}}^2}\)
-
C
\({\rm{16c}}{{\rm{m}}^2}\)
-
D
\({\rm{32c}}{{\rm{m}}^2}\)
Cho hình thang \(ABCD\,\left( {AB // CD} \right)\) có \(BC = 18{\rm{ cm,}}\,AD = 12{\rm{ cm}}\) . Điểm \(E\) thuộc cạnh \(AD\) sao cho \(AE = 6{\rm{ cm}}\) . Qua \(E\) kẻ đường thẳng song song với \(CD\) , cắt \(BC\) ở \(F\) . Tính độ dài \(BF\) .
-
A
9 cm
-
B
10 cm
-
C
11 cm
-
D
12 cm
Cho tam giác \(ABC\) có đường cao \(AH\) . Trên \(AH\) lấy các điểm \(K,\,I\) sao cho \(AK = KI = IH\). Qua \(I,\,K\) lần lượt vẽ các đường thẳng \(EF // BC,\,MN // BC\) \(\left( {E,\,M \in AB;\,F,\,N \in AC} \right)\) . Cho biết diện tích của tam giác \(ABC\) là \(90\,{\rm{c}}{{\rm{m}}^2}\) . Hãy tính diện tích tứ giác \(MNF\) .
-
A
\(30\,{\rm{c}}{{\rm{m}}^2}\)
-
B
\(60\,{\rm{c}}{{\rm{m}}^2}\)
-
C
\(90\,{\rm{c}}{{\rm{m}}^2}\)
-
D
\(120\,{\rm{c}}{{\rm{m}}^2}\)
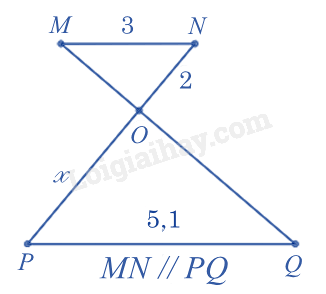
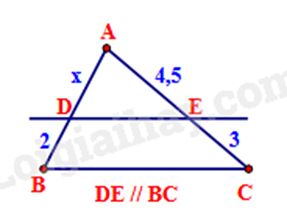
-
A
\(x = 3,3\).
-
B
\(x = 3,4\).
-
C
\(x = 3,5\).
-
D
\(x = 3,6\).
Cho tam giác ABC có \(AB = 9cm, AC = 6cm\) Vẽ \(AD\) là đường phân giác của góc \(A\) Biết \(CD = 2cm\) độ dài đoạn thẳng \(DB\) là:
-
A
\(1,5 \ cm\)
-
B
\(3 \ cm\)
-
C
\(4,5 \ cm\)
-
D
\(6 \ cm\)
Cho tam giác \(ABC\), trên \(AB\) lấy \(M\) sao cho \(AM = 6\,cm\), \(MB = 4\,cm\). Qua \(M\) kẻ đường thẳng song song với \(BC\) cắt \(AC\) tại \(N\), biết \(AC = 20\,cm\). Độ dài đoạn thẳng \(AN\) là
-
A
\(10\, cm\);
-
B
\(12\, cm\);
-
C
\(8\, cm\);
-
D
\(6\, cm\).
Cho hình vẽ, biết \(DE\parallel AC\). Khẳng định nào sau đây là đúng?
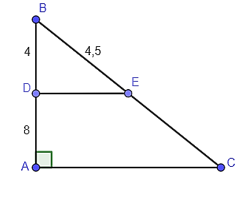
-
A
\(BC=13,5\);
-
B
\(BC=12\);
-
C
\(EC = 7\);
-
D
\(EC=8\).
Cho hình vẽ, biết \(MN\parallel BC\), \(ND\parallel AB\), \(BC = 9\). Độ dài \(y\) trong hình gần với giá trị nào dưới đây?
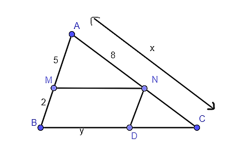
-
A
\(4,63\, cm\);
-
B
\(6,34\, cm\);
-
C
\(6,43\, cm\);
-
D
\(4,36\, cm\).
Cho tam giác \(ABC\) có đường cao \(AH\). Trên \(AH\) lấy các điểm \(K,\, I\) sao cho \(AK = KI = IH\). Qua \(I,\, K\) lần lượt vẽ các đường thẳng \(EF\parallel BC\), \(MN\parallel BC\) (\(E,\,M \in AB\); \(F,N \in AC\)). Khi đó \(\frac{{AE}}{{AB}} + \frac{{AN}}{{AF}}\) bằng
-
A
\( \frac{1}{2}\);
-
B
\( \frac{1}{3}\);
-
C
\( \frac{2}{3}\);
-
D
\( \frac{7}{6}\).
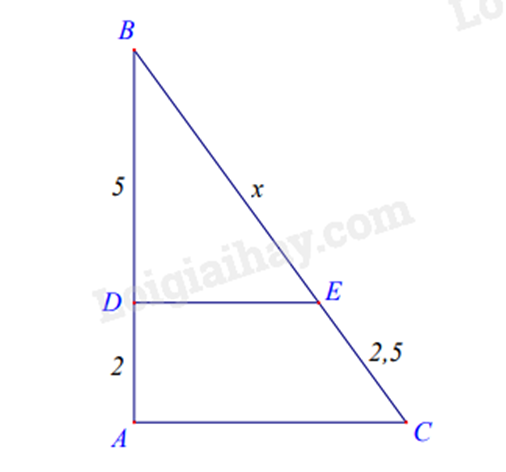
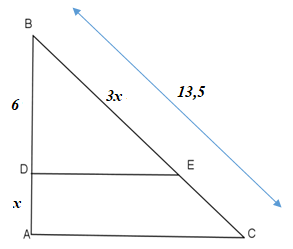
-
A
\(x = 5\).
-
B
\(x = 6,25\).
-
C
\(x = 8\).
-
D
\(x = 6,5\).
Cho tam giác ABC, trên hai cạnh AB, AC lấy hai điểm E, F sao cho EF // BC. Biết AE = 6cm, BE = 4cm, CF = 6cm. Khi đó độ dài AF bằng
-
A
4cm.
-
B
9cm.
-
C
12cm.
-
D
8cm.
-
A
x = 4,5.
-
B
x = 3.
-
C
x = 1,33.
-
D
x = 6,75.