Trắc nghiệm Chứng minh các bài toán liên quan Toán 7 có đáp án
Trắc nghiệm Chứng minh các bài toán liên quan
Cho \(\Delta ABC = \Delta MNP.\) Biết AC = 6 cm, NP = 8 cm và chu vi của tam giác MNP bằng 22cm. Tìm khẳng định sai:
-
A
MP = 8 cm
-
B
BC = 8 cm
-
C
MN = 8 cm
-
D
AB = 8 cm
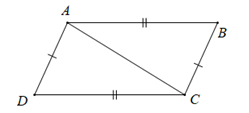
-
A
\(AD//BC\)
-
B
\(AB//CD\)
-
C
\(\Delta ABC = \Delta CDA\)
-
D
\(\Delta ABC = \Delta ADC\)
Cho \(\Delta\)ABC có AB = AC và MB = MC (\(M \in BC\)).Chọn câu sai.
-
A
\(\Delta AMC = \Delta BCM\)
-
B
\(AM \bot BC\)
-
C
\(\widehat {BAM} = \widehat {CAM}\)
-
D
\(\Delta AMB = \Delta AMC\)
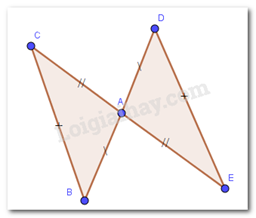
-
A
\(\Delta ABC = \Delta DEA\)
-
B
\(\widehat D = \widehat A\)
-
C
\(\widehat E = \widehat B\)
-
D
\(\widehat C = \widehat E\)
Cho tam giác \(ABC\) có \(AB < AC\) . Gọi \(E \in AC\) sao cho \(AB = CE\). Gọi \(O\) là một điểm nằm ở trong tam giác sao cho \(OA = OC,OB = OE.\) Khi đó:
-
A
\(\Delta AOB = \Delta CEO\)
-
B
\(\Delta AOB = \Delta COE\)
-
C
\(\widehat {AOB} = \widehat {OEC}\)
-
D
\(\widehat {ABO} = \widehat {OCE}\)
Cho tam giác ABC và tam giác MNP có AB = MP, AC = NM, BC = NP. Khẳng định nào dưới đây đúng?
-
A
∆ABC = ∆MNP;
-
B
∆ABC = ∆NMP;
-
C
∆ABC = ∆PMN;
-
D
∆ABC = ∆MPN.
Cho tam giác \(ABC\) và tam giác \(MNP\) có \(\widehat A = \widehat {M,}\widehat B = \widehat N\) . Cần thêm điều kiện gì để tam giác \(ABC\) và tam giác \(MNP\) bằng nhau theo trường hợp góc – cạnh – góc:
-
A
\(AC = MP\)
-
B
\(AB = MN\)
-
C
\(BC = NP\)
-
D
\(AC = MN\)
Cho góc nhọn \(xOy,Oz\) là tia phân giác của góc đó. Qua điểm \(A\) thuộc tia \(Ox\) kẻ đường thẳng song song với \(Oy\) cắt \(Oz\) ở \(M.\) Qua \(M\)kẻ đường thẳng song song với \(Ox\) cắt \(Oy\) ở \(B.\) Chọn câu đúng.
-
A
\(OA > OB;MA > MB\)
-
B
\(OA = OB;MA = MB\)
-
C
\(OA < OB;MA < MB\)
-
D
\(OA < OB;MA = MB\)
Cho hai đoạn thẳng \(BD\) và \(EC\) vuông góc với nhau tại \(A\) sao cho \(AB = AE,AD = AC,AB < AC.\) Phát biểu nào trong các phát biểu sau đây là sai:
-
A
\(\Delta AED = \Delta ABC\)
-
B
\(BC = ED\)
-
C
\(EB = CD\)
-
D
\(\widehat {ABC} = \widehat {AED}\) .
Cho góc nhọn \(xOy.\) Trên tia \(Ox\) lấy hai điểm \(A,C,\) trên tia \(Oy\) lấy hai điểm \(B,D\) sao cho \(OA = OB,OC = OD\) (\(A\) nằm giữa \(O\) và \(C,\)\(B\) nằm giữa \(O\) và \(D\) ). So sánh hai góc \(\widehat {CAD}\) và \(\widehat {CBD}.\)
-
A
\(\widehat {CBD} = \widehat {CAD}\)
-
B
\(\widehat {CBD} < \widehat {CAD}\)
-
C
\(\widehat {CBD} > \widehat {CAD}\)
-
D
\(2.\widehat {CBD} = \widehat {CAD}\)
Cho tam giác \(ABC\) có \(AB = AC = BC,\) phân giác \(BD\) và \(CE\) cắt nhau tại \(O.\) Tính \(\widehat {BOC}.\)
-
A
\({60^0}\)
-
B
\({80^0}\)
-
C
\(120^\circ \)
-
D
\({100^0}\)
Cho hai đoạn thẳng \(AB\) và \(CD\) cắt nhau tại \(O\) là trung điểm của mỗi đoạn thẳng đó. Lấy \(E;\,F\) lần lượt là điểm thuộc đoạn \(AD\) và \(BC\) sao cho \(AE = BF.\) Cho \(OE = 2cm\), tính \(EF.\)
-
A
\(4\,cm\)
-
B
\(2cm\)
-
C
\(3\,cm\)
-
D
\(3,5\,cm\)
Cho tam giác \(ABC\) có \(AB = AC.\) Trên các cạnh \(AB\) và \(AC\) lấy các điểm \(D,E\) sao cho \(AD = AE.\) Gọi \(K\) là giao điểm của \(BE\) và \(CD\). Chọn câu sai.
-
A
\(BE = CD\)
-
B
\(BK = KC\)
-
C
\(BD = CE\)
-
D
\(DK = KC\)
Cho tam giác \(DEF\) và tam giác \(HKG\) có \(\widehat D = \widehat H\), \(\widehat E = \widehat K\), \(DE = HK.\) Biết \(\widehat F = {80^0}\). Số đo góc \(G\) là:
-
A
\({70^0}\)
-
B
\({80^0}\)
-
C
\({90^0}\)
-
D
\({100^0}\)
Cho tam giác \(ABC\) vuông tại \(A\) có \(AB = AC.\) Qua \(A\) kẻ đường thẳng \(xy\) sao cho \(B,C\) nằm cùng phía với \(xy.\) Kẻ \(BD\) và \(CE\) vuông góc với \(xy.\) Chọn câu đúng.
-
A
\(DE = BD + CE\)
-
B
\(DE = BD - CE\)
-
C
\(CE = BD + DE\)
-
D
\(CE = BD - DE\)