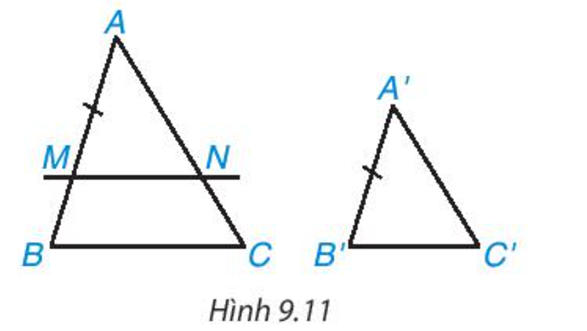
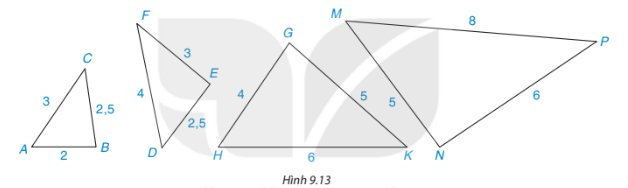
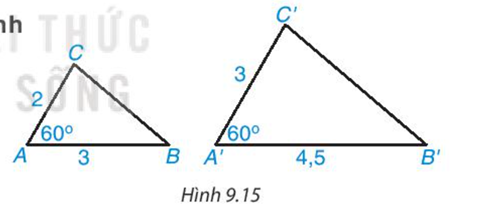
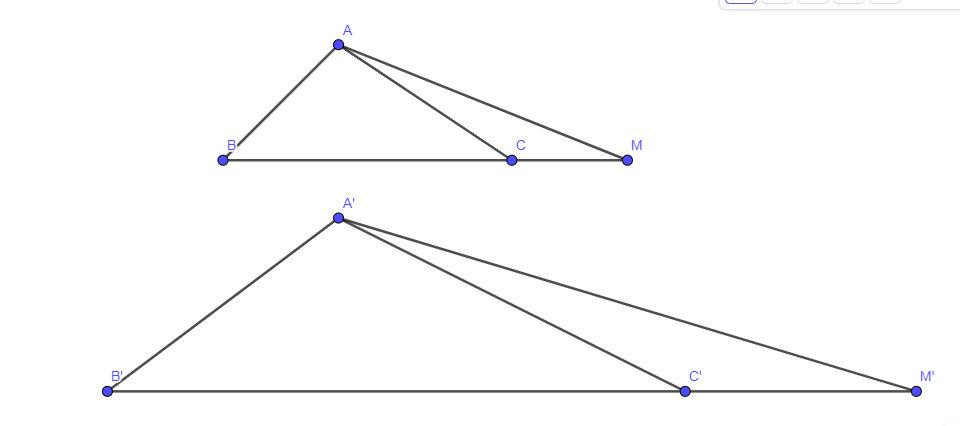
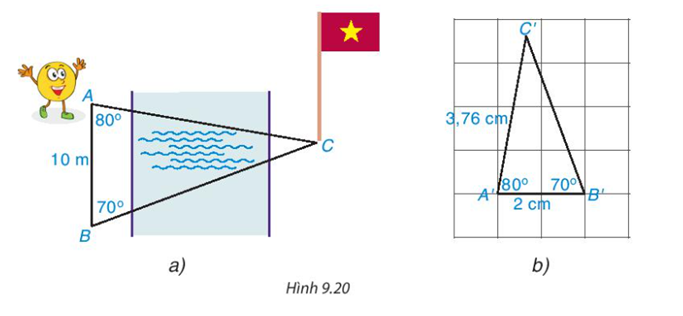
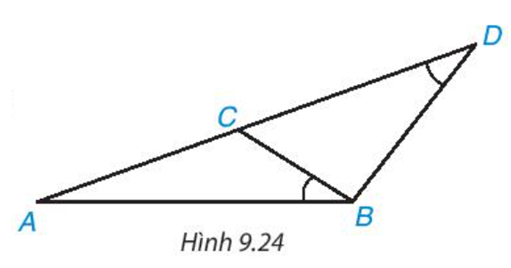
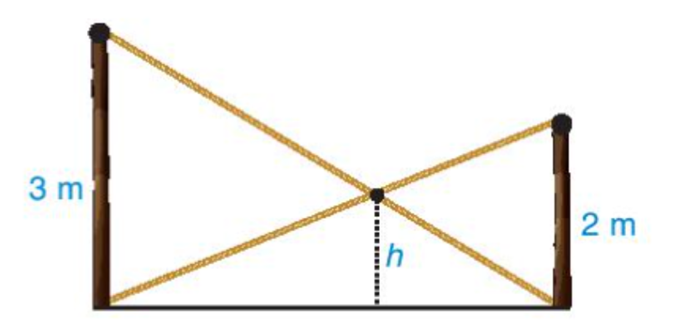
Giải SGK, SBT, VTH Toán 8 Bài 34. Ba trường hợp đồng dạng của hai tam giác Kết nối tri thức

Cho hai tam giác ABC và A'B'C' có \(\frac{{A'B'}}{{AB}} = \frac{{A'C'}}{{AC}} = \frac{{B'C'}}{{BC}}\)

a) Nếu A′B=AB thì hai tam giác có đồng dạng với nhau không? Vì sao?

b) Nếu A′B < AB như hình 9.11. Trên đoạn thẳng AB lấy điểm M sao cho AM = A'B'. Kẻ đường thẳng qua M song song với BC và cắt AC tại N.

- Hãy giải thích vì sao ΔAMN ∽ ΔABC

- Hãy chứng tỏ rằng AN=A’C’′, MN=B′C′ để suy ra ΔAMN = ΔA'B'C' (c.c.c)

- Hai tam giác A'B'C' và ABC có đồng dạng với nhau không? Nếu có, em hãy viết đúng kí hiệu đồng dạng giữa chúng.

c) Nếu A'B' > AB thì tam giác A'B'C' có đồng dạng với tam giác ABC không? Vì sao?

Những cặp tam giác nào dưới đây (hình 9.13) là đồng dạng? (các kích thước được tính theo đơn vị centimét). Viết đúng kí hiệu đồng dạng.

Cho tam giác ABC có chu vi bằng 18 cm và tam giác DEF có chu vi bằng 27cm. Biết rằng AB=4cm, BC=6cm, DE=6cm, FD=12cm. Chứng minh  ΔABC ∽ ΔDEF

Trở lại tình huống mở đầu. Em hãy vẽ một tam giác có ba cạnh tỉ lệ với ba cạnh của tam giác tạo bởi ba đỉnh là trái bóng và hai chân cột gôn. Từ đó tính góc sút bằng góc tương ứng của tam giác vừa vẽ được.

Cho hai tam giác ABC và A'B'C' có độ dài các cạnh (theo đơn vị cm) như Hình 9.15. Biết rằng \(\widehat A = \widehat {A'} = 60^0\)

- So sánh các tỉ số \(\frac{{A'B'}}{{AB}}{;^{}}\frac{{A'C'}}{{AC}}\)

- Dùng thước có vạch chia đo độ dài BC, B'C' và tính tỉ số \( \frac {B′C′} {BC} \)

- Theo em, tam giác A'B'C' có đồng dạng với tam giác ABC không? Nếu có thì tỉ số đồng dạng là bao nhiêu?

Những cặp tam giác nào trong hình 9.17 là đồng dạng? (Các kích thước được tính theo đơn vị centimét). Viết đúng kí hiệu đồng dạng.

Cho ΔA'B'C' ∽ ΔABC. Trên tia đối của các tia CB, C'B' lần lượt lấy các điểm M, M' sao cho \(\frac{{MC}}{{MB}} = \frac{{M'C'}}{{M'B'}}\). Chứng minh rằng  ΔA'B'M' ∽ ΔABM

Bạn Lan nhận xét rằng nếu tam giác ABC và tam giác A’B’C’ có \(\frac{{A'B'}}{{AB}} = \frac{{A'C'}}{{AC}}\) và \(\widehat {B'} = \widehat B\) thì chúng đồng dạng. Theo em bạn Lan nhận xét đúng không vì sao?

Gợi ý. Khi góc ACB tù, lấy điểm M trên tia BC sao cho \( \Delta AMC \) cân (H.9.19) rồi xét xem trong hai tam giác ABC và ABM, tam giác nào đồng dạng với tam giác A'B'C'.

Bạn Tròn đang đứng ở vị trí điểm A bên bờ sông và nhờ anh Pi tính giúp khoảng cách từ chỗ mình đứng đến chân một cột cờ tại điểm C bên kia sông (H.9.20a). Anh Pi lấy một vị trí B sao cho AB=10m, \(\widehat {ABC} = {70^o}{,^{}}\widehat {BAC} = {80^o}\) và vẽ một tam giác A'B'C' trên giấy với A′B′=2cm, \(\widehat {A'B'C'} = {70^o};\widehat {B'A'C'} = {80^o}\)(H.9.20b)

Em hãy dự đoán xem tam giác A'B'C' có đồng dạng với tam giác ABC không? nếu có thì tỉ số đồng dạng là bao nhiêu

Nếu ΔABC ∽ ΔA′B′C′ và anh Pi đo được A′C′=3,76cm thì khoảng cách từ bạn Tròn đến chân cột cờ là bao nhiêu mét? 

Những cặp tam giác nào trong hình 9.22 là đồng dạng? Viết đúng kí hiệu đồng dạng

Cho các điểm A, B, C, D như Hình 9.24. Biết rằng \(\widehat {ABC} = \widehat {A{\rm{D}}B}\). Hãy chứng minh ΔABC ∽ ΔADB  và \(A{B^2} = A{\rm{D}}.AC\)

1. Biết rằng ba đường phân giác của tam giác ABC đồng quy tại I, ba đường phân giác của tam giác A'B'C' đồng quy tại I'. Hãy chứng tỏ rằng nếu \( \widehat {A'I'B'} = \widehat {AIB} \) và \( \widehat {A'I'C'} = \widehat {AIC} \) thì \( \Delta A'B'C' \backsim \Delta ABC \).

2. Với  hai tam giác ABC và A'B'C' trong phần Tranh luận, nếu thêm giả thiết các góc C và C' nhọn thì hai tam giác đó có đồng dạng không?

Giả thiết nào dưới đây chứng tỏ rằng hai tam giác đồng dạng?

a) Ba cạnh của tam giác này tỉ lệ với ba cạnh của tam giác kia.

b) Hai cạnh của tam giác này tỉ lệ với hai cạnh của tam giác kia và có một cặp góc bằng nhau.

c) Hai góc của tam giác này bằng hai góc của tam giác kia.

d) Hai cạnh của tam giác này bằng hai cạnh của tam giác kia.

Cho hai tam giác đồng dạng. Tam giác thứ nhất có độ dài ba cạnh là 4cm, 8cm và 10cm. Tam giác thứ hai có chu vi là 33cm. Độ dài ba cạnh của tam giác thứ hai là bộ ba nào sau đây?

a) 6cm, 12cm, 15cm

b) 8cm, 16cm, 20cm

c) 6cm, 9cm, 18cm

d) 8cm, 10cm, 15cm

Cho AM, BN, CP là các đường trung tuyến của tam giác ABC. Cho A'M', B'N', C'P' là các đường trung tuyến của tam giác A'B'C'. Biết rằng ΔA’B’C’ ∽ ΔABC 

Chứng minh rằng \(\frac{{A'M'}}{{AM}} = \frac{{B'N'}}{{BN}} = \frac{{C'P'}}{{CP}}\)

Cho tam giác ABC có AB=12cm, AC=15cm. Trên các tia AB, AC lần lượt lấy các điểm M, N sao cho AM=10cm, AN=8cm. Chứng minh rằng ΔABC ∽ ΔANM.

Cho góc BAC và các điểm M, N lần lượt trên các đoạn thẳng AB, AC sao cho \(\widehat {ABN} = \widehat {ACM}\)

a) Chứng minh rằng ΔABN ∽ ΔACM

b) Gọi I là giao điểm của BN và CM. Chứng minh rằng IB.IN=IC.IM

Có hai chiếc cột dựng thẳng đứng trên mặt đất với chiều cao lần lượt là 3m và 2m. Người ta nối hai sợi dây từ đỉnh cột này đến chân cột kia và hai sợi dây cắt nhau tại một điểm (H.9.25), hãy tính độ cao h của điểm đó so với mặt đất.

Hai tam giác có độ dài ba cạnh như sau có đồng dạng không? Vì sao?

(1) 2cm, 3cm, 4cm và 6cm, 9cm, 12cm.

(2) 3cm, 5cm, 6cm và 6cm, 10cm, 11cm.

(3) 2cm, 3cm, 3cm và 2cm, 2cm, 3cm.

(4) 4cm, 4cm, 4cm và 3cm, 3cm, 3cm.

Cho hai tam giác ABC và DEF lần lượt có chu vi là 15cm và 20cm. Biết rằng \(\frac{{AB}}{{DE}} = \frac{{AC}}{{DF}} = \frac{3}{4}.\) Chứng minh rằng $\Delta ABC\backsim \Delta DEF$

Cho hai tam giác ABC và DEF thỏa mãn \(2AB = 3AC = 4BC\) và \(DE = 6cm,\;DF = 4cm,\;EF = 3cm.\) Chứng minh $\Delta ABC\backsim \Delta DEF$

Cho tam giác ABC và điểm O nằm trong tam giác. Lấy M, N, P là các điểm lần lượt trên các tia OA, OB, OC sao cho \(OA = 3OM,OB = 3ON,OC = 3OP.\) Chứng minh rằng $\Delta ABC\backsim \Delta MNP$ và tìm tỉ số đồng dạng

Cho tam giác ABC có các điểm M, N, P lần lượt là trung điểm của BC, CA, AB. Chứng minh rằng $\Delta ABC\backsim \Delta MNP$ và tìm tỉ số đồng dạng.

Cho tứ giác ABCD với \(AB = 2cm,AD = 3cm,BD = 4cm,BC = 6cm,CD = 8cm\). Chứng minh rằng $\Delta ABD\backsim \Delta BDC$ và AB song song với CD.

Cho tam giác ABC có độ dài các cạnh là \(AB = 4cm,BC = 5cm,CA = 6cm.\) Tam giác MNP đồng dạng với tam giác ABC và có độ dài cạnh lớn nhất bằng 9cm. Hãy cho biết độ dài các cạnh MN, MP, NP của tam giác MNP.

Với hai tam giác ABC và DEF bất kì thỏa mãn \(\frac{{AB}}{{EF}} = \frac{{BC}}{{DF}},\widehat {ABC} = \widehat {DFE}\). Những khẳng định nào sau đây là đúng?

(1) $\Delta ABC\backsim \Delta DEF$

(2) $\Delta CAB\backsim \Delta DEF$

(3) $\Delta ABC\backsim \Delta EFD$

(4) $\Delta BCA\backsim \Delta EFD$

(5) $\Delta ABC\backsim \Delta FDE$

(6) $\Delta BAC\backsim \Delta FED$

Với hai tam giác bất kì ABC và MNP thỏa mãn \(\widehat {ABC} = \widehat {NMP},\widehat {ACB} = \widehat {MNP}\). Những khẳng định nào sau đây là đúng?

(1) $\Delta ABC\backsim \Delta MNP$

(2) $\Delta BCA\backsim \Delta MNP$

(3) $\Delta ABC\backsim \Delta NPM$

(4) $\Delta CAB\backsim \Delta NPM$

(5) $\Delta ABC\backsim \Delta PMN$

(6) $\Delta BAC\backsim \Delta MNP$

Cho hai điểm M, N lần lượt nằm trên hai cạnh AB, AC của tam giác ABC sao cho \(AM.AB = AN.AC\).

a) Chứng minh rằng $\Delta AMN\backsim \Delta ACB$

b) Lấy E, F lần lượt là trung điểm của MN, BC. Chứng minh rằng \(\widehat {EAB} = \widehat {FAC}\)

Cho tam giác ABC và hai điểm P, Q lần lượt nằm trên các tia đối của tia AB và AC sao cho \(\widehat {APQ} = \widehat {ACB}\). Chứng minh rằng:

a) \(AP.AB = AQ.AC\)

b) $\Delta APC\backsim \Delta AQB$

Cho tam giác ABC và hai điểm M, N lần lượt nằm trên AB, AC sao cho MN song song với BC. Gọi ME, BF lần lượt là phân giác của các góc M, B của các tam giác AMN và tam giác ABC. Chứng minh rằng:

a) $\Delta MEN\backsim \Delta BFC$

b) \(\frac{{AE}}{{AF}} = \frac{{MN}}{{BC}}\)

Cho hình thang ABCD (AB//CD). Biết rằng \(AB = 2cm,BD = 4cm,CD = 8cm.\) Chứng minh rằng \(BC = 2AD\)

Cho hình thang ABCD (AB//CD). Biết rằng AD cắt BC tại E, AC cắt BD tại F.

a) Chứng minh rằng: $\Delta EAB\backsim \Delta EDC,\Delta FAB\backsim \Delta FCD$.

b) Lấy hai điểm M, N lần lượt là trung điểm của AB, CD. Chứng minh rằng bốn điểm M, N, E, F thẳng hàng.

Cho tam giác ABC với \(AB = 6cm,AC = 9cm.\) Lấy điểm D trên cạnh AC sao cho \(AD = 4cm.\) Chứng minh rằng $\Delta ABD\backsim \Delta ACB$ và \(BC = \frac{3}{2}BD\)

Cho tứ giác ABCD như hình 9.6. Biết rằng \(AB = 2cm,AC = 4cm,AD = 8cm\) và AC là phân giác của góc BAD. Chứng minh \(CD = 2BC\)

Hình 9.6

Cho tam giác ABC và điểm D trên cạnh AC sao cho \(\widehat {ABD} = \widehat {BCA}.\) Chứng minh rằng: \(A{B^2} = AD.AC\)

Cho hai điểm M, N lần lượt nằm trên hai cạnh AB, AC của tam giác ABC sao cho \(\widehat {ABN} = \widehat {ACM}.\) Gọi O là giao điểm của BN và CM. Chứng minh rằng:

a) \(AM.AB = AN.AC\)

b) \(OM.OC = ON.OB\)

Cho tam giác ABC với \(AB = 6cm,AC = 4cm,BC = 5cm.\) Trên tia đối của tia CA, lấy điểm D sao cho \(CD = CB\). Chứng minh rằng:

a) $\Delta ABC\backsim \Delta ADB$

b) \(\widehat {ACB} = 2\widehat {ABC}\)

Cho tam giác ABC có AB = 4cm, BC = 5cm, CA = 6cm. Bộ ba độ dài nào dưới đây là độ dài ba cạnh của một tam giác đồng dạng với tam giác ABC với tỉ số đồng dạng là 2.

A. 2cm, 2,5cm, 3cm.

B. 4cm, 5cm, 6cm.

C. 8cm, 10cm, 12cm.

D. 6cm, 8cm, 10cm.

Với hai tam giác bất kì ABC và DEF thỏa mãn $\frac{AB}{DE}=\frac{AC}{DF},\widehat{BAC}=\widehat{FDE}$, khẳng định nào sau đây là đúng?

A. $\Delta CAB\backsim \Delta DEF$.

B. $\Delta ABC\backsim \Delta EFD$.

C. $\Delta BCA\backsim \Delta EFD$.

D. $\Delta BAC\backsim \Delta FED$.

Với hai tam giác bất kì ABC và MNP thỏa mãn \(\widehat{ABC}=\widehat{PNM},\widehat{ACB}=\widehat{NPM}\), khẳng định nào sau đây là đúng?

A. $\Delta ABC\backsim \Delta MNP$.

B. $\Delta ABC\backsim \Delta NPM$.

C. $\Delta ABC\backsim \Delta PNM$.

D. $\Delta ACB\backsim \Delta NPM$.

Giả thiết nào dưới đây chứng tỏ rằng hai tam giác đồng dạng?

a) Ba cạnh của tam giác này tỉ lệ với ba cạnh của tam giác kia.

b) Hai cạnh của tam giác này tỉ lệ với hai cạnh của tam giác kia và có một cặp góc bằng nhau.

c) Hai góc của tam giác này bằng hai góc của tam giác kia.

d) Hai cạnh của tam giác này bằng hai cạnh của tam giác kia.

Cho hai tam giác đồng dạng. Tam giác thứ nhất có độ dài ba cạnh là 4cm, 8cm và 10cm. Tam giác thứ hai có chu vi là 33cm. Độ dài ba cạnh của tam giác thứ hai là bộ ba nào sau đây?

a) 6cm, 12cm, 15cm

b) 8cm, 16cm, 20cm

c) 6cm, 9cm, 18cm

d) 8cm, 10cm, 15cm

Cho AM, BN, CP là các đường trung tuyến của tam giác ABC. Cho A'M', B'N', C'P' là các đường trung tuyến của tam giác A'B'C'. Biết rằng ΔA’B’C’ ∽ ΔABC 

Chứng minh rằng \(\frac{{A}'{M}'}{AM}=\frac{{B}'{N}'}{BN}=\frac{{C}'{P}'}{CP}\).

Cho tam giác ABC có AB = 12cm, AC = 15cm. Trên các tia AB, AC lần lượt lấy các điểm M, N sao cho AM = 10cm, AN = 8cm. Chứng minh rằng ΔABC ∽ ΔANM.

Cho góc BAC và các điểm M, N lần lượt trên các đoạn thẳng AB, AC sao cho \(\widehat{ABN}=\widehat{ACM}\)

a) Chứng minh rằng ΔABN ∽ ΔACM.

b) Gọi I là giao điểm của BN và CM. Chứng minh rằng IB.IN = IC.IM.

Có hai chiếc cột dựng thẳng đứng trên mặt đất với chiều cao lần lượt là 3m và 2m. Người ta nối hai sợi dây từ đỉnh cột này đến chân cột kia và hai sợi dây cắt nhau tại một điểm (H.9.25), hãy tính độ cao h của điểm đó so với mặt đất.

Cho tam giác ABC và điểm O nằm trong tam giác. Lấy các điểm M, N, P lần lượt là trung điểm của các đoạn thẳng OA, OB, OC. Chứng minh rằng $\Delta ABC\backsim \Delta MNP$ và tìm tỉ số đồng dạng.

Cho hai điểm M, N lần lượt nằm trên hai cạnh AB, AC của tam giác ABC sao cho AM.AB = AN.AC. Chứng minh rằng $\Delta AMN\backsim \Delta ACB$ và $\Delta AMC\backsim \Delta ANB.$

Cho tam giác ABC và hai điểm P, Q lần lượt nằm trên các cạnh AB và AC sao cho \(\widehat{ABQ}=\widehat{ACP}\). Chứng minh rằng $\Delta APC\backsim \Delta AQB$ và $\Delta APQ\backsim ACB$.