Hoạt động 6 trang 82 Tài liệu dạy – học Toán 9 tập 1Giải bài tập Cho tam giác đều ABC có cạnh bằng 2 dm. Gọi D là trung điểm BC. Tính độ dài AD, CD rồi Quảng cáo
Đề bài
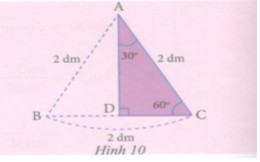
Cho tam giác đều ABC có cạnh bằng 2 dm. Gọi D là trung điểm BC. Tính độ dài AD, CD rồi dùng kết quả đó để tính tỉ số lượng giác của các góc \({30^0}\) và \({60^0}\). Lời giải chi tiết Ta có D là trung điểm BC \( \Rightarrow CD = \dfrac{1}{2}BC = 1\,dm\) Áp dụng định lý Pythagore vào tam giác ADC vuông tại D có: \(A{D^2} + C{D^2} = A{C^2}\\ \Rightarrow AD = \sqrt {A{C^2} - C{D^2}} = \sqrt 3 \,\,dm\) Xét tam giác ADC vuông tại D có: \(\begin{array}{l}\sin {30^o} = \cos {60^o} = \dfrac{{CD}}{{AC}} = \dfrac{1}{2}\,\,;\\\cos {30^o} = \sin {60^o} = \dfrac{{AD}}{{AC}} = \dfrac{{\sqrt 3 }}{2}\\\tan {30^o} = \cot {60^o} = \dfrac{{CD}}{{AD}} = \dfrac{{\sqrt 3 }}{3}\,\,;\\\cot {30^o} = \tan {60^o} = \dfrac{{AD}}{{CD}} = \sqrt 3 \end{array}\) Loigiaihay.com  Chia sẻ Bình luận
Quảng cáo
Tham Gia Group 2K10 Ôn Thi Vào Lớp 10 Miễn Phí
|
