Mục III,IV - Phần A - Trang 125,126 Vở bài tập Vật lí 9Giải trang 125,126 VBT vật lí 9 Mục III - Độ lớn của ảnh tạo bởi các thấu kính, mục IV - Vận dụng (Phần A - Học theo SGK) với lời giải chi tiết các câu hỏi và lý thuyết trong bài 45 Quảng cáo
Đề bài Hoàn thành mục III - Độ lớn của ảnh tạo bởi thấu kính và mục IV - Vận dụng Lời giải chi tiết III - ĐỘ LỚN CỦA ẢNH ẢO TẠO BỞI THẤU KÍNH C5: + Thấu kính là hội tụ: Ảnh của vật AB tạo bởi thấu kính hội tụ lớn hơn vật.
+ Thấu kính là phân kì: Ảnh của vật AB tạo bởi thấu kính phân kì nhỏ hơn vật.
IV - VẬN DỤNG C6: Phân biệt ảnh ảo ở thấu kính hội tụ và phân kỳ: - Giống nhau: Cùng chiều với vật. - Khác nhau: + Đối với thấu kính hội tụ thì ảnh lớn hơn vật và ở xa thấu kính hơn vật. + Đốì với thâu kính phân kì thì ảnh nhỏ hơn vật và ở gần thấu kính hơn vật.
Cách nhận biết nhanh chóng một thấu kính hội tụ hay phân kì: Đưa thấu kính lại gần dòng chữ trên trang sách. Nếu nhìn qua thấu kính thấy hình ảnh dòng chữ cùng chiều, to hơn so với khi nhìn trực tiếp thì đó là thấu kính hội tụ. Ngược lại, nếu nhìn thấy hình ảnh dòng chữ cùng chiều, nhỏ hơn so với nhìn trực tiếp thì đó là thấu kính phân kì. C7: Trường hợp 1- thấu kính hội tụ
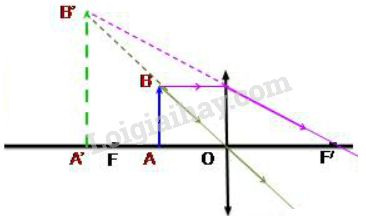
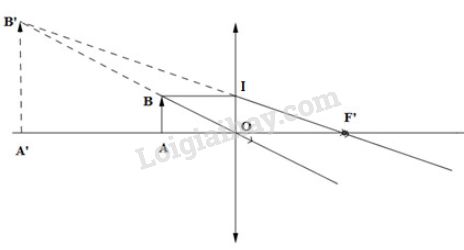
+ Ta có: \(\Delta BB'I \sim \Delta OB'F'\) Ta suy ra: \(\dfrac{{BI}}{{OF'}} = \dfrac{{BB'}}{{OB'}}\) (1) Theo đề bài, ta có: \(OA = BI = 8cm\), \(OF' = 12cm\) Lại có: \(OB' = OB + BB'\) Ta suy ra \(\left( 1 \right) \Leftrightarrow \dfrac{8}{{12}} = \dfrac{{BB'}}{{OB + BB'}}\) \(\begin{array}{l} \Rightarrow \dfrac{{12}}{8} = \dfrac{{OB + BB'}}{{BB'}}\\ \Rightarrow 1,5 = \dfrac{{OB}}{{BB'}} + 1\end{array}\) \( \Rightarrow \dfrac{{OB}}{{BB'}} = 0,5 \Rightarrow \dfrac{{BB'}}{{OB}} = 2\) (2) + Ta có: \(\Delta OA'B' \sim \Delta OAB\) Ta suy ra: \(\dfrac{{OA'}}{{OA}} = \dfrac{{A'B'}}{{AB}} = \dfrac{{OB'}}{{OB}}\) (3) Ta có \(OB' = OB + BB'\) Ta suy ra \(\left( 3 \right) \Leftrightarrow \dfrac{{OA'}}{{OA}} = \dfrac{{A'B'}}{{AB}} = \dfrac{{OB + BB'}}{{OB}} = 1 + \dfrac{{BB'}}{{OB}}\) Thế (2) vào (3) ta được: \(\dfrac{{OA'}}{{OA}} = \dfrac{{A'B'}}{{AB}} = 1 + 2 = 3\) Từ đây ta suy ra: - Khoảng cách từ ảnh đến thấu kính: \(OA' = 3.OA = 3.8 = 24cm\) - Chiều cao của ảnh: \(A'B' = 3.AB = 3.6 = 18mm\) Vậy ảnh có chiều cao \(18mm\) (cao gấp 3 lần vật) cách thấu kính một khoảng là \(24cm\) + Trường hợp 2: Thấu kính phân kì
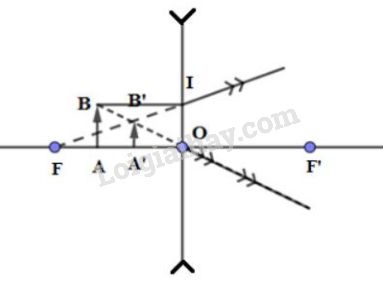
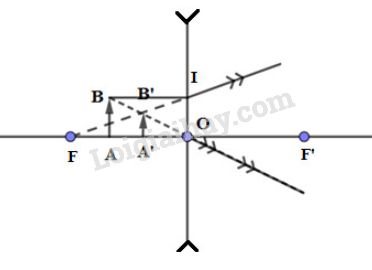
+ Ta có: \(\Delta IB'B \sim \Delta FB'O\) Ta suy ra: \(\dfrac{{IB}}{{FO}} = \dfrac{{B'B}}{{B'O}}\) Theo đầu bài ta có: \(IB = AO = 8cm\) và \(FO = 12cm\) Ta suy ra: \(\dfrac{8}{{12}} = \dfrac{{B'B}}{{B'O}} \Rightarrow \dfrac{{B'B}}{{B'O}} = \dfrac{2}{3}\) (1) + Ta có: \(\Delta OAB \sim \Delta OA'B'\) Ta suy ra: \(\dfrac{{OA}}{{OA'}} = \dfrac{{OB}}{{OB'}} = \dfrac{{AB}}{{A'B'}}\) Lại có: \(OB = OB' + BB'\) Ta suy ra: \(\dfrac{{OA}}{{OA'}} = \dfrac{{AB}}{{A'B'}} = \dfrac{{OB' + BB'}}{{OB'}} = 1 + \dfrac{{BB'}}{{OB'}}\) (2) Từ (1) và (2) ta suy ra: \(\dfrac{{OA}}{{OA'}} = \dfrac{{AB}}{{A'B'}} = 1 + \dfrac{2}{3} = \dfrac{5}{3}\) Từ đây, ta suy ra: - Khoảng cách từ ảnh đến thấu kính: \(OA' = \dfrac{{OA}}{{\dfrac{5}{3}}} = \dfrac{8}{{\dfrac{5}{3}}} = 4,8cm\) - Chiều cao của ảnh: \(A'B' = \dfrac{{AB}}{{\dfrac{5}{3}}} = \dfrac{6}{{\dfrac{5}{3}}} = 3,6mm\) Vậy, ảnh có chiều cao \(3,6mm\) (cao gấp \(0,6\) lần vật) và cách thấu kính một khoảng là \(4,8cm\) C8: Bạn Đông bị cận thị nặng. Nếu Đông bỏ kính ra, ta nhìn thấy mắt bạn to hơn khi nhìn thấy mắt bạn đang đeo kính, vì kính của bạn là thấu kính phân kì. Khi ta nhìn mắt bạn qua thấu kính phân kì, ta đã nhìn thấy ảnh ảo của mắt, nhỏ hơn mắt khi không đeo kính. Loigiaihay.com
|




















Danh sách bình luận