Giải mục 2 trang 72, 73, 74, 75 Chuyên đề học tập Toán 11 - Chân trời sáng tạo

Khám phá 2

Trong Hình 7, theo em, nếu chỉ dùng một hình chiếu vuông góc của hình hộp chữ nhật ℋ trên một trong ba mặt phẳng đôi một vuông góc (P₁), (P₂), (P₃) có đủ để chế tạo được ℋ không?

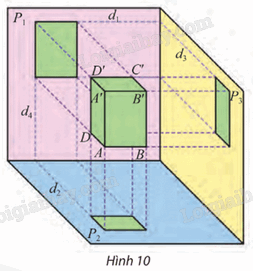
Phương pháp giải:

Quan sát hình 7, suy luận thực tiễn để trả lời.

Lời giải chi tiết:

Ta thấy nếu chỉ dùng một hình chiếu vuông góc của hình hộp chữ nhật ℋ trên một trong ba mặt phẳng đôi một vuông góc (P₁), (P₂), (P₃) trong Hình 7 thì hình chiếu đó chỉ thể hiện được một mặt của vật thật dẫn đến chế tạo không chính xác.

Vậy nếu chỉ dùng một hình chiếu vuông góc của hình hộp chữ nhật ℋ trên một trong ba mặt phẳng đôi một vuông góc (P₁), (P₂), (P₃) thì không đủ để chế tạo được hình ℋ.

Khám phá 3

Quan sát Hình 10 và cho biết:

– Trong ba cạnh AB, AA’ và AD của hình hộp chữ nhật, cạnh nào song song với một trong ba mặt phẳng chiếu (P₁), (P₂), (P₃)?

– Tìm hai giao tuyến của (P₁) và (P₂) với mặt phẳng đi qua điểm D và vuông góc với cả (P₁) và (P₂).

Phương pháp giải:

Quan sát hình 10 để trả lời.

Lời giải chi tiết:

– Trong ba cạnh AB, AA’ và AD của hình hộp chữ nhật ABCD.A’B’C’D’, ta có:

⦁ Cạnh AB song song với các mặt phẳng chiếu (P₁) và (P₂);

⦁ Cạnh AA’ song song với các mặt phẳng chiếu (P₁) và (P₃);

⦁ Cạnh AD song song với các mặt phẳng chiếu (P₂) và (P₃).

Vậy cả ba cạnh AB, AA’ và AD của hình hộp chữ nhật đều song song với một trong ba mặt phẳng chiếu (P₁), (P₂) và (P₃).

– Xác định hai giao tuyến của (P₁) và (P₂) với mặt phẳng đi qua điểm D và vuông góc với cả (P₁) và (P₂):

Ta có AD ⊥ AA’ (do ABCD.A’B’C’D’ là hình hộp chữ nhật).

Mà AA’ // (P₁).

Suy ra AD ⊥ (P₁).

Do đó (AA’D’D) ⊥ (P₁).

Chứng minh tương tự, ta được (AA’D’D) ⊥ (P₂).

Vì vậy mặt phẳng đi qua điểm D và vuông góc với cả (P₁) và (P₂) là (AA’D’D).

Gọi D₁, D₁’ lần lượt là hình chiếu vuông góc của các điểm D, D’ lên mặt phẳng (P₁).

Suy ra D₁, D₁’∈ (AA’D’D) và D₁, D₁’∈ (P₁).

Do đó hay d₄ = (AA’D’D) ∩ (P₁).

Chứng minh tương tự, ta được d₂ = (AA’D’D) ∩ (P₂).

Vậy d₄, d₂ lần lượt là hai giao tuyến cần tìm.

Thực hành 2

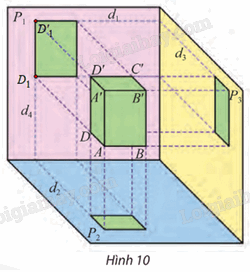
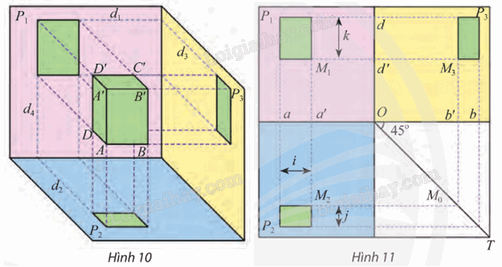
a) Trên Hình 10, độ dài cạnh AD được bảo toàn trên các hình chiếu nào của bản vẽ? Tại sao?

b) Trên Hình 11, tìm hai giao tuyến được biểu diễn thành đường gióng a trên bản vẽ.

c) Trên Hình 11, khoảng cách giữa hai đường gióng nào cho ta chiều cao AA’ của vật ở Hình 10?

Phương pháp giải:

Quan sát hình 10, 11 để trả lời.

Lời giải chi tiết:

a) Trên Hình 10, độ dài cạnh AD được bảo toàn trên hình chiếu bằng và hình chiếu cạnh của bản vẽ vì AD song song với (P₂) và (P₃).

b) Hai giao tuyến được biểu diễn thành đường gióng a trên Hình 11 là d₄ và d₂.

c) Trên Hình 11, ta thấy độ dài mũi tên k bằng chiều cao AA’ của vật ở Hình 10.

Vậy trên Hình 11, khoảng cách giữa hai đường gióng d và d’ cho ta chiều cao AA’ của vật ở Hình 10.

Vận dụng 2

Trong bản vẽ biểu diễn hình nón trong Hình 12.

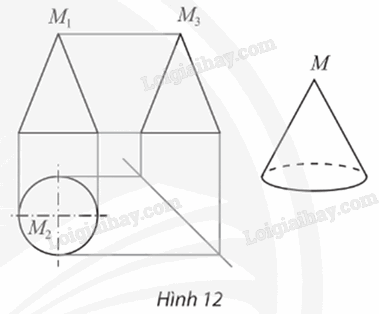
a) Khoảng cách giữa hai đường gióng nào cho ta biết chiều cao của hình nón?

b) Khoảng cách giữa hai đường gióng nào cho ta biết độ dài đường kính đáy của hình nón?

c) Nêu cách xác định điểm M₃ biểu diễn đỉnh M của hình nón trong hình chiếu cạnh khi biết hai điểm M₁ và M₂ biểu diễn M trong hình chiếu đứng và hình chiếu bằng.

Phương pháp giải:

Quan sát hình 12, suy luận để trả lời.

Lời giải chi tiết:

Gọi d₁, d₂, d₃, d₄, d₅ là các đường gióng của bản vẽ (như hình vẽ).

a) Khoảng cách giữa hai đường gióng d₁ và d₂ cho ta biết chiều cao của hình nón.

b) Khoảng cách giữa hai đường gióng d₃ và d₄ cho ta biết độ dài đường kính đáy của hình nón.

c) Gọi OT là đường phân giác của bản vẽ (như hình vẽ).

– Phác họa đường gióng qua M₂ và song song với d₁, đường gióng này cắt OT tại M₀.

– Phác họa đường gióng d₅ qua M₀ và song song với M₁M₂.

Giao điểm của d₅ và d₁ là điểm M₃ cần tìm.