Giải mục 1 trang 6, 7, 8, 9 Chuyên đề học tập Toán 12 - Kết nối tri thức

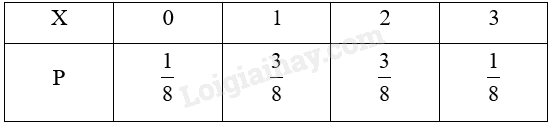
Hoạt động 1

Trả lời câu hỏi Hoạt động 1 trang 6 Chuyên đề học tập Toán 12 Kết nối tri thức

Gieo một con xúc xắc cân đối, đồng chất liên tiếp 6 lần. Gọi \(X\)là số lần xúc xắc xuất hiện mặt 6 chấm trong 6 lần gieo liên tiếp đó

a) Các giá trị có thể của \(X\) là gì?

b) Trước khi thực hiện việc gieo xúc xắc đó, ta có khẳng định trước được \(X\) sẽ nhận giá trị nào không?

Phương pháp giải:

Dựa vào thực nghiệm gieo một con xúc xắc 6 lần

Lời giải chi tiết:

a) \(X \in \left\{ {0;1;2;3;4;5;6} \right\}\).

b) Ta không thể khẳng định trước được.

Hoạt động 2

Trả lời câu hỏi Hoạt động 2 trang 7 Chuyên đề học tập Toán 12 Kết nối tri thức

Hãy nêu số thích hợp với dấu “?” để hoàn thành bảng phân bố xác suất của biến ngẫu nhiên rời rạc \(X\) trong Ví dụ 1.

Phương pháp giải:

Dựa vào HĐ1, ta điền các kết quả tương ứng vào bảng

Lời giải chi tiết:

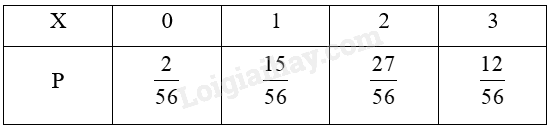
Luyện tập 1

Trả lời câu hỏi Luyện tập 1 trang 9 Chuyên đề học tập Toán 12 Kết nối tri thức

Một tổ có 10 học sinh nam và 6 học sinh nữ. Giáo viên chọn ngẫu nhiên đồng thời 3 học sinh. Gọi X là số học sinh nam trong 3 học sinh được chọn. Lập bảng phân bố xác suất của X.

Phương pháp giải:

Bước 1: Liệt kê các giá trị có thể của X

Bước 2: Tính các xác suất để X nhận các giá trị đó

Bước 3: Lập bảng phân bố xác suất cho biến ngẫu nhiên X

Lời giải chi tiết:

Các giá trị của X có thể nhận được thuộc tập {0; 1; 2; 3}. 

Số kết quả có thể là \(C_{16}^3 = 560.\)

+ Biến cố \(\left\{ {X = 0} \right\}\) là: “Không có HS nam nào trong 3 HS được chọn”

Số cách chọn 3 học sinh nữ: \(C_6^3 = 20\) (cách chọn)

Do đó, \(P\left( {X = 0} \right)\; = \frac{{20}}{{560}} = \frac{2}{{56}}\)

+ Biến cố \(\left\{ {X = 1} \right\}\) là: “Chọn được 1 học sinh nam và 2 học sinh nữ”

Số cách chọn 1 học sinh nam và 2 học sinh nữ: \(C_{10}^1.C_6^2 = 150\) (cách chọn)

Do đó, \(P\left( {X = 1} \right)\; = \frac{{150}}{{560}} = \frac{{15}}{{56}}\)

+ Biến cố \(\left\{ {X = 2} \right\}\) là: “Chọn được 2 học sinh nam và 1 học sinh nữ”

Số cách chọn 2 học sinh nam và 1 học sinh nữ: \(C_{10}^2.C_6^1 = 270\) (cách chọn)

Do đó, \(P\left( {X = 2} \right)\; = \frac{{270}}{{560}} = \frac{{27}}{{56}}\)

+ Biến cố \(\left\{ {X = 3} \right\}\) là : “Chọn được 3 học sinh nam”

Số cách chọn 3 học sinh nam: \(C_{10}^3 = 120\) (cách chọn)

Do đó,  \(P\left( {X = 3} \right)\; = \frac{{120}}{{560}} = \frac{{12}}{{56}}\)

Ta có bảng phân phối xác suất của X là:

Vận dụng 1

Trả lời câu hỏi Vận dụng 1 trang 9 Chuyên đề học tập Toán 12 Kết nối tri thức

Một trò chơi sử dụng một hộp đựng 20 quả cầu có kích thước và khối lượng như nhau được ghi số từ 1 đến 20. Người chơi lấy ngẫu nhiên đồng thời 3 quả cầu trong hộp. Gọi X là số lớn nhất ghi trên 3 quả cầu đã lấy ra.

a) Lập bảng phân bố xác suất của X.

b) Người chơi thắng cuộc nếu trong 3 quả cầu lấy ra có ít nhất 1 quả cầu ghi số lớn hơn 18. Tính xác suất thắng của người chơi.

Phương pháp giải:

Làm theo hướng dẫn trong sách

Lời giải chi tiết:

a) Tập các giá trị có thể của X là {3; 4;...; 20}

Số kết quả có thể là \(C_{20}^3 = 1140.\)

Biến cố \(\left\{ {X = k} \right\}\) là biến cố: “Trong 3 quả cầu lấy ra có 1 quả cầu đánh số \(k\) và 2 quả cầu đánh số nhỏ hơn \(k\)”. Số kết quả thuận lợi là: \(C_{k - 1}^2\)

Vậy \(P\left( {X = k} \right) = \frac{{C_{k - 1}^2}}{{C_{20}^3}} = \frac{{(k - 1)(k - 2)}}{{2280}}\)

Bảng phân bố xác suất của X là:

b) Biến cố: “Người chơi thắng” là biến cố hợp của hai biến cố \(A = \left\{ {X = 19} \right\}\) và \(B = \left\{ {X = 20} \right\}\)

Vì \(A,B\) là hai biến cố xung khắc nên

\(P(A \cup B) = P(A) + P(B){\rm{ = }}P(X = 19) + P(X = 20) = 0,134 + 0,15 = 0,284\)