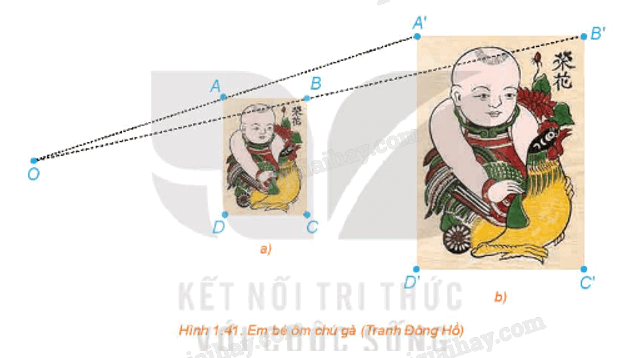
Giải mục 1 trang 26, 27 Chuyên đề học tập Toán 11 - Kết nối tri thứcTrong hai bức tranh ở Hình 1.41, các hình chữ nhật ABCD, A'B'C'D' có các cạnh tương ứng song song, bức tranh lớn có kích thước gấp đôi bức tranh nhỏ. Quảng cáo
Lựa chọn câu để xem lời giải nhanh hơn
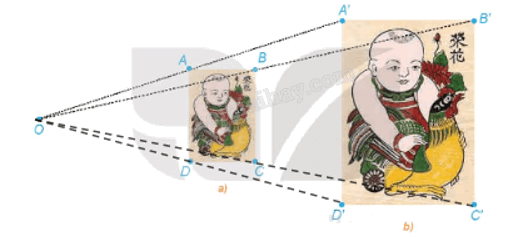
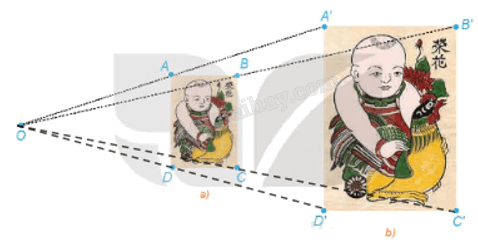
Hoạt động 1 Trong hai bức tranh ở Hình 1.41, các hình chữ nhật ABCD, A'B'C'D' có các cạnh tương ứng song song, bức tranh lớn có kích thước gấp đôi bức tranh nhỏ. a) Giải thích vì sao các đường thẳng AA', BB', CC', DD' cùng đi qua một điểm O. b) Hãy tính các tỉ số \(\frac{{OA}}{{OA'}},\,\frac{{OB}}{{OB'}},\,\frac{{OC}}{{OC'}},\,\frac{{OD}}{{OD'}}\). c) Dùng thước thẳng nối hai điểm tương ứng nào đó trên hai bức tranh (chẳng hạn, đầu mỏ trên của chú gà ở hai bức tranh). Đường thẳng đó có đi qua O hay không?
Phương pháp giải: Dựa vào định lí Thalès để chứng minh A, B, C, D lần lượt là trung điểm của A’O, B’O, C’O, D’O. Lời giải chi tiết:
a) Gọi O là giao điểm của AA' và BB'. Xét tam giác OA'B' có AB // A'B', theo định lý Thales, ta có: \(\frac{{OA}}{{OA'}} = \frac{{OB}}{{OB'}} = \frac{{AB}}{{A'B'}} = \frac{1}{2}\) Từ đó suy ra A, B lần lượt là trung điểm của OA' và OB'. Gọi C" là giao điểm của BC và OC'. Vì BC // B'C' nên BC" // B'C'. Xét tam giác OB'C' có BC" // B'C' và B là trung điểm của OB' nên BC" là đường trung bình của tam giác OB'C'. Suy ra và C" là trung điểm của OC'. Mặt khác theo giả thiết ta có \(BC = \frac{1}{2}B'C'\). Do vậy C" trùng với C và C là trung điểm của OC'. Chứng minh tương tự, ta được D là trung điểm của OD'. Vậy các đường thẳng AA', BB', CC', DD' cùng đi qua một điểm O. b) Vì A, B, C, D lần lượt là trung điểm của OA', OB', OC', OD' nên \(\frac{{OA}}{{OA'}} = \frac{{OB}}{{OB'}} = \frac{{AB}}{{A'B'}} = \frac{1}{2}\). c) Dùng thước thẳng nối hai điểm tương ứng trên hai bức tranh, cụ thể, đầu mỏ trên của chú gà ở hai bức tranh, ta thấy đường thẳng này đi qua điểm O. Câu hỏi Phép vị tự \({V_{(O,{\rm{ }}k)}}\) biến điểm O thành điểm nào? Nếu phép vị tự \({V_{(O,{\rm{ }}k)}}\) biến điểm M thành điểm M' thì phép vị tự \({V_{\left( {O,\frac{1}{k}} \right)}}\) biến điểm M' thành điểm nào? Phương pháp giải: Nếu phép vị tự tâm O tỉ số k \(\left( {k \ne 0} \right)\) lần lượt biến 2 điểm A, B thành 2 điểm A’, B’ thì \(A'B' = \left| k \right|AB\) Lời giải chi tiết: - Phép vị tự \({V_{(O,{\rm{ }}k)}}\) biến điểm O thành điểm O. - Nếu phép vị tự \({V_{(O,{\rm{ }}k)}}\) biến điểm M thành điểm M' thì phép vị tự \({V_{\left( {O,\frac{1}{k}} \right)}}\) biến điểm M' thành điểm M. Thật vậy, nếu M' là ảnh M qua phép vị tự \({V_{(O,{\rm{ }}k)}}\) thì \(\overrightarrow {OM'} = k\overrightarrow {OM} \Leftrightarrow \overrightarrow {OM} = \frac{1}{k}\overrightarrow {OM'} \). Điều này có nghĩa là M là ảnh của M' qua phép vị tự \({V_{\left( {O,\frac{1}{k}} \right)}}\). Luyện tập 1 Chứng minh rằng, phép vị tự \({V_{(O,{\rm{ }}1)}}\) là phép đồng nhất, phép vị tự \({V_{\left( {o,-1} \right)}}\;\) là phép đối xứng tâm O. Phương pháp giải: Nếu phép vị tự tâm O tỉ số k \(\left( {k \ne 0} \right)\) lần lượt biến 2 điểm A, B thành 2 điểm A’, B’ thì \(A'B' = \left| k \right|AB\) Lời giải chi tiết: + Phép vị tự \({V_{(O,{\rm{ }}1)}}\) biến điểm M thành điểm M' thỏa mãn \(\overrightarrow {OM'} = \overrightarrow {OM} \). Khi đó M' trùng với M. Do đó, phép vị tự \({V_{(O,{\rm{ }}1)}}\) là phép đồng nhất. + Phép vị tự \({V_{\left( {o,-1} \right)}}\;\) biến điểm M thành điểm M" thỏa mãn . Khi đó O là trung điểm của MM". Do đó, M" là ảnh của M qua phép đối xứng tâm O hay phép vị tự \({V_{\left( {o,-1} \right)}}\;\) là phép đối xứng tâm O. Vận dụng 1 Quan sát hai bức tranh em bé ôm chú gà ở phần mở đầu bài học và chỉ ra phép vị tự biến bức tranh nhỏ thành bức tranh lớn và phép vị tự biến bức tranh lớn thành bức tranh nhỏ. Phương pháp giải: Quan sát hình ảnh và tìm tỉ số k Nếu phép vị tự tâm O tỉ số k \(\left( {k \ne 0} \right)\) lần lượt biến 2 điểm A, B thành 2 điểm A’, B’ thì \(A'B' = \left| k \right|AB\) Lời giải chi tiết:
Ta có: \(\frac{{OA}}{{OA'}} = \frac{{OB}}{{OB'}} = \frac{{OC}}{{OC'}} = \frac{{OD}}{{OD'}} = \frac{1}{2}\) (theo HĐ1). Suy ra \(\overrightarrow {OA'} = 2\overrightarrow {OA} ;\,\overrightarrow {OB'} = 2\overrightarrow {OB} ;\,\overrightarrow {OC'} = 2\overrightarrow {OC} ;\,\overrightarrow {OD'} = 2\overrightarrow {OD} \). Từ đó ta có các điểm A', B', C', D' lần lượt là ảnh của các điểm A, B, C, D qua phép vị tự \({V_{\left( {O,2} \right)}}\). Do đó, phép vị tự V(O, 2) biến hình chữ nhật ABCD thành hình chữ nhật A'B'C'D'. Vậy phép vị tự \({V_{\left( {O,2} \right)}}\) biến bức tranh nhỏ thành bức tranh lớn. Khi đó, phép vị tự \({V_{\left( {O,\frac{1}{2}} \right)}}\) biến bức tranh lớn thành bức tranh nhỏ.
|





















Danh sách bình luận