Giải mục 1 trang 16, 17 Chuyên đề học tập Toán 11 - Kết nối tri thứcỞ mặt bàn ăn quay nói trên, trong một lần quay, nếu một đĩa thức ăn trên bàn được quay một phần tư vòng tới vị trí người mới Quảng cáo
Lựa chọn câu để xem lời giải nhanh hơn
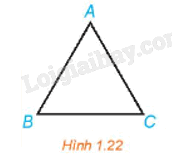
Hoạt động 1 Ở mặt bàn ăn quay nói trên, trong một lần quay, nếu một đĩa thức ăn trên bàn được quay một phần tư vòng tới vị trí người mới, thì mỗi đĩa không đặt ở chính giữa bàn có được quay một phần tư vòng tới vị trí mới hay không? Phương pháp giải: Suy luận thực tiễn để trả lời Lời giải chi tiết: Mỗi đĩa thức ăn không đặt ở chính giữa bàn nhưng đặt ở trên phần bàn xoay đều quay được một phần tư vòng tới vị trí mới. Mỗi đĩa thức ăn không đặt ở giữa bàn và không đặt ở trên phần bàn xoay thì không quay được một phần tư vòng tới vị trí mới. Câu hỏi Phép quay với góc quay bằng 0 có gì đặc biệt? Phương pháp giải: Dựa vào phép quay \({Q_{\left( {O,\alpha } \right)}}\) với \(\alpha = {0^o}\). Trong mặt phẳng, cho điểm O cố định và góc lượng giác \(\alpha \) không đổi. Phép biến hình biến điểm O thành điểm O và biến mỗi điểm M khác O thành M’ sao cho \(OM = OM'\) và góc lượng giác \(\left( {OM,OM'} \right) = \alpha \) được gọi là phép quay tâm O với góc quay \(\alpha \), kí hiệu \({Q_{\left( {O,\alpha } \right)}}\). O gọi là tâm quay, \(\alpha \) gọi là góc quay. Lời giải chi tiết: Phép quay tâm O với góc quay bằng 0 biến điểm O thành điểm O và biến mỗi điểm M khác O thành chính nó. Luyện tập 1 Trong Hình 1.22, tam giác ABC đều.
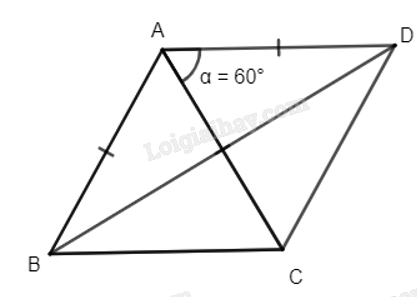
Hãy chỉ ra ảnh của điểm B qua phép quay \({Q_{\left( {A,{\rm{ }}60^\circ } \right)}}\) Gọi D là ảnh của C qua phép quay \({Q_{\left( {A,{\rm{ }}60^\circ } \right)}}\) Hỏi B và D có mối quan hệ gì đối với đường thẳng AC? Phương pháp giải: - Tam giác đều có 3 góc bằng \({60^o}\). - Trong mặt phẳng, cho điểm O cố định và góc lượng giác \(\alpha \) không đổi. Phép biến hình biến điểm O thành điểm O và biến mỗi điểm M khác O thành M’ sao cho \(OM = OM'\) và góc lượng giác \(\left( {OM,OM'} \right) = \alpha \) được gọi là phép quay tâm O với góc quay \(\alpha \), kí hiệu \({Q_{\left( {O,\alpha } \right)}}\). O gọi là tâm quay, \(\alpha \) gọi là góc quay. Lời giải chi tiết: Tam giác ABC đều nên AB = AC và \(\widehat {BAC} = 60^\circ \). Do đó phép quay \({Q_{\left( {A,{\rm{ }}60^\circ } \right)}}\) biến điểm B thành điểm C. Vì D là ảnh của C qua phép quay Q(A, 60°) nên AC = AD và \(\widehat {CAD} = 60^\circ \) Khi đó tam giác ACD là tam giác đều nên AC = AD = DC. Mà AB = AC = BC (tam giác ABC đều). Do đó, AB = BC = CD = AD, suy ra tứ giác ABCD là hình thoi. Khi đó hai đường chéo AC và BD vuông góc với nhau và cắt nhau tại trung điểm của mỗi đường nên AC là đường trung trực của đoạn thẳng BD. Vậy B và D đối xứng nhau qua đường thẳng AC hay B là ảnh của D qua phép đối xứng trục AC.
|




















Danh sách bình luận