A. Hoạt động thực hành - Bài 92 : Em ôn lại những gì đã họcGiải Bài 92: Em ôn lại những gì đã học phần hoạt động thực hành trang 78, 79 sách VNEN toán lớp 4 với lời giải dễ hiểu Quảng cáo
Lựa chọn câu để xem lời giải nhanh hơn
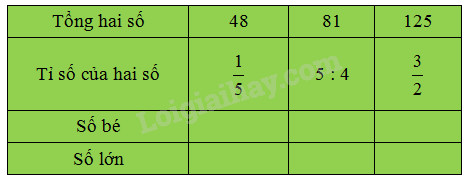
Câu 1 Chơi trò chơi: “Đố nhau trong nhóm” : Các bạn đố nhau: Cho hai số, viết tỉ số của chúng. Phương pháp giải: Áp dụng định nghĩa : Tỉ số của hai số a và b là a : b hay \(\dfrac{a}{b}\) (b khác 0). Lời giải chi tiết: • Tỉ số của 5 và 8 là 5 : 8 hay \(\dfrac{5}{8}.\) • Tỉ số của 14 và 27 là 14 : 27 hay \(\dfrac{{14}}{{27}}.\) • Tỉ số của 7cm và 9cm là 7 : 9 hay \(\dfrac{7}{9}.\) • Tỉ số của 24 tạ và 35 tạ là 24 : 35 hay \(\dfrac{{24}}{{35}}.\) Lưu ý : Khi viết tỉ số của hai số đo độ dài hay khối lượng thì các số đo đó phải cùng một đơn vị đo. Câu 2 Viết tỉ số của a và b, biết: a) a = 3 ; b = 8 ; b) a = 15m ; b = 11m ; c) a = 10kg ; b = 12kg. Phương pháp giải: Áp dụng định nghĩa : Tỉ số của hai số a và b là a : b hay \(\dfrac{a}{b}\) (b khác 0). Lời giải chi tiết: a) Tỉ số 3 và 8 là : 3 : 8 hay \(\dfrac{3}{8}\). b) Tỉ số 15m và 11m là : 15 : 11 hay \(\dfrac{{15}}{{11}}\). c) Tỉ số 10kg và 12kg là : 10 : 12 hay \(\dfrac{{10}}{{12}}\). Câu 3 Viết số thích hợp vào ô trống :
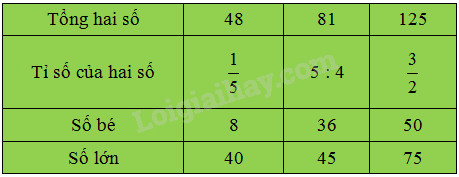
Phương pháp giải: Tính ra nháp theo các bước bên dưới, sau đó ghi kết quả vào bảng : 1. Vẽ sơ đồ dựa vào tỉ số của hai số. 2. Tìm tổng số phần bằng nhau. 3. Tìm giá trị của 1 phần bằng cách lấy tổng hai số chia cho tổng số phần bằng nhau. 4. Tìm số bé (lấy giá trị một phần nhân với số phần của số bé). 5. Tìm số lớn (lấy tổng hai số trừ đi số bé). Chú ý: Bước 3 và bước 4 có thể gộp lại thành một bước; có thể tìm số lớn trước rồi tìm số bé sau. Lời giải chi tiết:
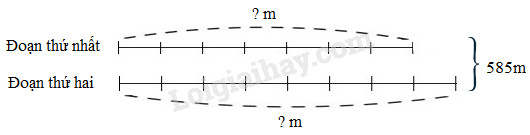
Câu 4 Một cuộn dây điện dài 585m. Người bán hàng cắt thành hai đoạn, đoạn thứ nhất bằng \(\dfrac{7}{8}\) đoạn thứ hai. Hỏi mỗi đoạn dài bao nhiêu mét ? Phương pháp giải: 1. Vẽ sơ đồ: coi độ dài đoạn thứ nhất (đóng vai trò số bé) gồm 7 phần bằng nhau thì độ dài đoạn thứ hai (đóng vai trò số lớn) gồm 8 phần như thế. 2. Tìm tổng số phần bằng nhau. 3. Tìm giá trị của 1 phần bằng cách lấy tổng hai số chia cho tổng số phần bằng nhau. 4. Tìm số bé (lấy giá trị một phần nhân với số phần của số bé). 5. Tìm số lớn (lấy tổng hai số trừ đi số bé). Chú ý: Bước 3 và bước 4 có thể gộp lại thành một bước; có thể tìm số lớn trước rồi tìm số bé sau. Lời giải chi tiết: Ta có sơ đồ :
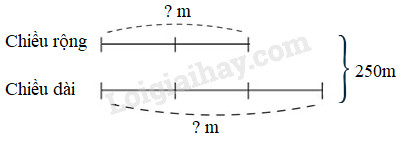
Theo sơ đồ, tổng số phần bằng nhau là : 7 + 8 = 15 (phần) Giá trị mỗi phần là : 585 : 15 = 39 (m) Đoạn dây thứ nhất dài số mét là : 39 × 7 = 273 (m) Đoạn dây thứ hai dài số mét là : 585 – 273 = 312 (m) Đáp số : Đoạn thứ nhất : 273m ; Đoạn thứ hai : 312m. Câu 5 Một hình chữ nhật có chu vi là 500m, chiều rộng bằng \(\dfrac{2}{3}\) chiều dài. Tìm chiều dài và chiều rộng hình chữ nhật Phương pháp giải: 1. Tìm nửa chu vi ta lấy chu vi chia cho 2. 2. Vẽ sơ đồ: coi chiều rộng (đóng vai trò số bé) gồm 2 phần bằng nhau thì chiều dài (đóng vai trò số lớn) gồm 3 phần như thế. 3. Tìm tổng số phần bằng nhau. 4. Tìm giá trị của 1 phần bằng cách lấy tổng hai số chia cho tổng số phần bằng nhau. 5. Tìm số bé (lấy giá trị một phần nhân với số phần của số bé). 6. Tìm số lớn (lấy tổng trừ đi số bé). Chú ý: Bước 4 và bước 5 có thể gộp lại thành một bước; có thể tìm số lớn trước rồi tìm số bé sau. Lời giải chi tiết: Nửa chu vi hình chữ nhật là : 500 : 2 = 250 (m) Ta có sơ đồ :
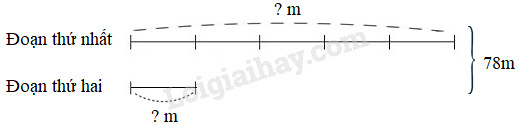
Theo sơ đồ, tổng số phần bằng nhau là : 2 + 3 = 5 (phần) Giá trị mỗi phần là : 250 : 5 = 50 (m) Chiều dài của hình chữ nhật là : 50 × 3 = 150 (m) Chiều rộng của hình chữ nhật là : 250 – 150 = 100 (m) Đáp số : Chiều dài : 150m ; Chiều rộng : 100m. Câu 6 Một sợi dây thừng dài 78m được cắt thành hai đoạn, đoạn thứ nhất dài gấp 5 lần đoạn thứ hai. Hỏi mỗi đoạn dây dài bao nhiêu mét? Phương pháp giải: 1. Vẽ sơ đồ: coi độ dài đoạn thứ hai (đóng vai trò số bé) gồm 1 phần thì độ dài đoạn thứ nhất (đóng vai trò số lớn) gồm 5 phần như thế. 2. Tìm tổng số phần bằng nhau. 3. Tìm giá trị của 1 phần bằng cách lấy tổng hai số chia cho tổng số phần bằng nhau. 4. Tìm số bé (lấy giá trị một phần nhân với số phần của số bé). 5. Tìm số lớn (lấy tổng hai số trừ đi số bé). Chú ý: Bước 3 và bước 4 có thể gộp lại thành một bước; có thể tìm số lớn trước rồi tìm số bé sau. Lời giải chi tiết: Ta có sơ đồ :
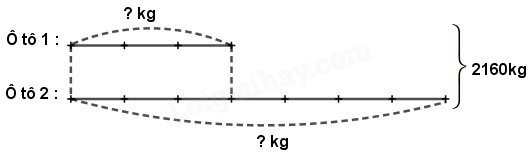
Theo sơ đồ, tổng số phần bằng nhau là : 5 + 1 = 6 (phần) Giá trị mỗi phần là : 78 : 6 = 13 (m) Đoạn thứ nhất dài số mét là : 13 × 5 = 65 (m) Đoạn thứ hai dài số mét là : 78 – 15 = 13 (m) Đáp số: Đoạn thứ nhất : 65m ; Đoạn thứ hai : 13m. Câu 7 Dựa vào sơ đồ sau, nêu bài toán rồi giải bài toán đó:
Phương pháp giải: - Quan sát sơ đồ tìm tỉ số và tổng của hai số, sau đó nêu bài toán thích hợp. - Giải bài toán: 1. Tìm tổng số phần bằng nhau. 2. Tìm giá trị của 1 phần bằng cách lấy tổng hai số chia cho tổng số phần bằng nhau. 3. Tìm số bé (lấy giá trị một phần nhân với số phần của số bé). 4. Tìm số lớn (lấy tổng hai số trừ đi số bé). Chú ý: Bước 2 và bước 3 có thể gộp lại thành một bước; có thể tìm số lớn trước rồi tìm số bé sau. Lời giải chi tiết: Nêu bài toán: Hai ô tô chở được tất cả 2160kg hàng. Số hàng ô tô thứ nhất chở được bằng \(\dfrac{3}{7}\) số hàng ô tô thứ hai chở được. Hỏi mỗi ô tô chở được bao nhiêu ki-lô-gam hàng ? Bài giải: Theo sơ đồ, tổng số phần bằng nhau là : 3 + 7 = 10 (phần) Giá trị mỗi phần là : 2160 : 10 = 216 (kg) Ô tô thứ nhất chở được số ki-lô-gam hàng là : 216 × 3 = 648 (kg) Ô tô thứ hai chở được số ki-lô-gam hàng là : 2160 – 648 = 1512 (kg) Đáp số: Ô tô thứ nhất : 648kg ; Ô tô thứ hai : 1512 kg. Loigiaihay.com
|



















Danh sách bình luận