Giải đề thi học kì 1 toán lớp 12 năm 2019 - 2020 sở giáo dục Vĩnh Phúc

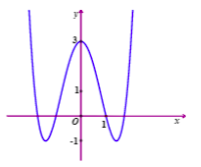
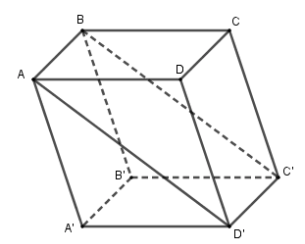
I. PHẦN TRẮC NGHIỆM: (3,0 điểm).

Câu 1. Cho hàm số \(y = f\left( x \right)\) có đạo hàm \(f'\left( x \right) = 3{x^2} + 1,\forall x \in \mathbb{R}.\)Chọn khẳng định đúng trong các khẳng định sau

A.Hàm số \(y = f\left( x \right)\) đồng biến trên khoảng \(\left( {0; + \infty } \right)\) và nghịch biến trên khoảng \(\left( { - \infty ;0} \right).\)

B. Hàm số \(y = f\left( x \right)\) đồng biến trên khoảng \(\left( { - \infty ;0} \right)\) và nghịch biến trên khoảng

\(\left( {0; + \infty } \right)\).

C.Hàm số \(y = f\left( x \right)\) nghịch biến trên \(\mathbb{R}.\)

D. Hàm số \(y = f\left( x \right)\) đồng biến trên \(\mathbb{R}.\)

Câu 2. Cho hình hộp chữ nhật \(ABCD.A'B'C'D'.\) Mặt phẳng nào sau đây chia hình hộp chữ nhật thành hai phần có thể tích bằng nhau?

A.\(\left( {ABC'D'} \right).\)             B.\(\left( {A'C'B} \right).\)

C. \(\left( {ACB'} \right).\)                D. \(\left( {BDA'} \right).\)

Câu 3. Số đường tiệm cận của đồ thị hàm số \(y = \dfrac{{x - 2}}{{2x + 1}}\) là

A.\(0.\)                                    B.\(3.\)

C. \(1.\)                                   D. \(2.\)

Câu 4. Số cạnh của hình bát diện đều là :

A. \(10.\)                                    B. \(6.\)

C.\(8\).                                       D. \(12.\)

Câu 5. Giá trị nhỏ nhất của hàm số \(y = x + \dfrac{4}{x}\) trên khoảng \(\left( {0; + \infty } \right)\) bằng

A.\(3.\)                        B.\(4.\)

C. \(5.\)                        D. \(1.\)

Câu 6. Giá trị lớn nhất của hàm số \(y = {x^3} - 3x + 2\) trên đoạn \(\left[ { - 3;3} \right]\) bằng

A.\(20.\)                        B.\(4.\)

C. \(0.\)                          D. \( - 16.\)

Câu 7. Tính giá trị biểu thức \(P = {9^{{{\log }_2}4}} - {8^{{{\log }_2}3}}\) .

A.\(P =  - 11.\)            B.\(P =  - 17.\)

C. \(P = 0.\)                D. \(P =  - 1.\)

Câu 8. Tính thể tích khối lăng trụ tam giác đều có tất cả các cạnh bằng \(a.\)

A.\(\dfrac{{\sqrt 3 {a^3}}}{6}.\)                   B.\(\dfrac{{\sqrt 3 {a^3}}}{4}.\)

C.\(\dfrac{{\sqrt 3 {a^3}}}{{12}}.\)                    D. \(\dfrac{{\sqrt 2 {a^3}}}{4}.\)

Câu 9. Cho khối chóp có diện tích đáy bằng \(B,\) chiều cao bằng \(h.\) Thể tích \(V\) của khối chóp đó là

A.\(V = \dfrac{B}{h}.\)                   B.\(V = \dfrac{{3B}}{h}\)

C. \(V = \dfrac{1}{3}B.h.\)             D. \(V = B.h.\)

Câu 10. Hàm số \(y = {x^3} - 3x\) nghịch biến trên khoảng nào sau đây ?

A.\(\left( {0; + \infty } \right).\)

B.\(\left( {1; + \infty } \right).\)

C.\(\left( { - 1;1} \right).\)

D. \(\left( { - \infty ;3} \right).\)

Câu 11. Hình vẽ bên là đồ thị của hàm số nào dưới đây ?

A.\(y =  - {x^4} - 2{x^2} + 3.\)                      B.\(y = {x^4} - 4{x^2} + 3.\)

C. \(y = {x^4} - 2{x^2} - 3.\)             D. \(y = {x^3} - 4{x^2} + 3.\)

Câu 12. Cho hàm số \(y = f\left( x \right)\) có bảng xét dấu đạo hàm như sau :

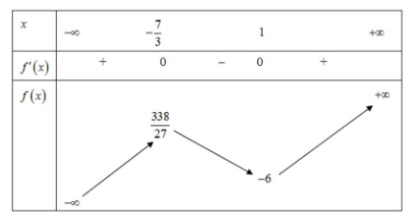
Hàm số \(y = f\left( x \right)\) nghịch biến trên khoảng nào trong các khoảng sau đây ?

A.\(\left( { - 2; + \infty } \right).\)                              B.\(\left( { - 2;1} \right).\)

C.\(\left( { - \infty ; - 2} \right).\)                               D. \(\left( {1;3} \right).\)

 II. TỰ LUẬN (7đ).

Câu 13 (1,0 điểm).  Gọi \(A,\,B\) là các điểm cực trị của đồ thị hàm số \(y = {x^3} + 3{x^2} - 4.\) Tính độ dài đoạn thẳng \(AB.\)

Câu 14 (1,0 điểm).  Rút gọn biểu thức \(P = \dfrac{{{a^{\sqrt 3  + 1}}.{a^{2 - \sqrt 3 }}}}{{{{\left( {{a^{\sqrt 2  - 2}}} \right)}^{\sqrt 2  + 2}}}},\) với \(a > 0.\) 

Câu 15 (1,0 điểm). Viết phương trình tiếp tuyến của đồ thị hàm số \(\left( C \right):y = \dfrac{{2x - 3}}{{x + 1}}\) tại giao điểm của \(\left( C \right)\) với trục tung.

Câu 16 (1,0 điểm). Tìm tất cả các giá trị của tham số \(m\) để đường thẳng \(d:y = 7x + m\) cắt đồ thị hàm số \(\left( C \right):y = {x^3} + 2{x^2} - 2\) tại \(3\) điểm phân biệt.

Câu 17 (1,0 điểm). Cho lăng trụ \(ABC.A'B'C'\) có đáy \(ABC\) là tam giác vuông tại \(B.\) Gọi \(H\) là chân đường cao kẻ từ \(B\) xuống \(AC,\) biết \(B'H \bot \left( {ABC} \right)\) và \(AB = 1,\,\,AC = 2,\,AA' = \sqrt 5 .\) Tính thể tích của khối lăng trụ đã cho.

Câu 18 (0,5 điểm). Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình vuông cạnh \(a,\) mặt bên \(SAB\) là tam giác đều và nằm trong mặt phẳng vuông góc với đáy. Tính thể tích khối chóp \(S.ABCD\) theo \(a.\)

 Câu 19 (0,5 điểm). Cho các số thực \(a,b\) thỏa mãn \(a > b > 1.\) Tìm giá trị nhỏ nhất của biểu thức \(P = \log _{\dfrac{a}{b}}^2\left( {ab} \right) + 12{\log _b}\left( {\dfrac{a}{b}} \right) - 2.\)

HƯỚNG DẪN GIẢI CHI TIẾT

Thực hiện: Ban chuyên môn Loigiaihay.com

PHẦN I: TRẮC NGHIỆM (3 điểm)

Câu 1 (NB)

Phương pháp:

Xét dấu đạo hàm tìm khoảng đồng biến nghịch biến.

Cách giải:

Ta có: \(f'\left( x \right) = 3{x^2} + 1 > 0,\forall x \in \mathbb{R}\) nên hàm số đồng biến trên \(\mathbb{R}\).

Chọn D.

Câu 2 (NB)

Phương pháp:

Dựng hình và nhận xét.

Cách giải:

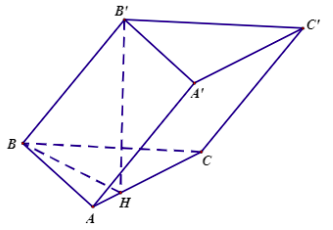
Từ hình vẽ ta thấy mặt phẳng \(\left( {ABC'D'} \right)\) chia hình hộp thành hai khối đa diện \(AA'D'.BB'C'\) và \(ADD'.BCC'\) có thể tích bằng nhau.

Chọn A.

Câu 3 (NB)

Phương pháp:

Hàm số phân thức \(y = \dfrac{{ax + b}}{{cx + d}}\left( {ad - bc \ne 0} \right)\) luôn có một đường tiệm cận đứng và một đường TCN.

Cách giải:

Đồ thị hàm số \(y = \dfrac{{x - 2}}{{2x + 1}}\) có TCĐ \(x =  - \dfrac{1}{2}\) và TCN \(y = \dfrac{1}{2}\).

Vậy có \(2\) đường tiệm cận.

Chọn D.

Câu 4 (NB)

Phương pháp:

Sử dụng lý thuyết hình bát diện đều.

Cách giải:

Hình bát diện đều có \(12\) cạnh.

Chọn D.

Câu 5 (TH)

Phương pháp:

Sử dụng bất đẳng thức Cô – si cho hai số dương \(a + b \ge 2\sqrt {ab} \).

Cách giải:

Ta có: \(x > 0\) nên \(x + \dfrac{4}{x} \ge 2\sqrt {x.\dfrac{4}{x}}  = 4\).

Dấu “=” xảy ra khi \(x = \dfrac{4}{x} \Leftrightarrow x = 2\).

Chọn B.

Câu 6 (TH)

Phương pháp:

- Tính đạo hàm \(y'\) và tìm nghiệm trong đoạn \(\left[ { - 3;3} \right]\).

- Tính giá trị của hàm số tại các điểm mút và nghiệm tìm được ở trên.

- So sánh kết quả và kết luận.

Cách giải:

Ta có: \(y' = 3{x^2} - 3 = 3\left( {{x^2} - 1} \right)\)

\(y' = 0 \Leftrightarrow x =  \pm 1 \in \left[ { - 3;3} \right]\)

Có \(y\left( { - 1} \right) = 4,y\left( 1 \right) = 0,\) \(y\left( { - 3} \right) =  - 16,y\left( 3 \right) = 20\)

Do đó \(\mathop {\max }\limits_{\left[ { - 3;3} \right]} y = 20\) khi \(x = 3\).

Chọn A.

Câu 7 (TH)

Phương pháp:

Sử dụng công thức \({a^{{{\log }_a}b}} = b\) và \({\log _a}{b^n} = n{\log _a}b\).

Cách giải:

Ta có: \({9^{{{\log }_3}4}} - {8^{{{\log }_2}3}} = {3^{2{{\log }_3}{2^2}}} - {2^{3{{\log }_2}3}}\) \( = {3^{4{{\log }_3}2}} - {2^{3{{\log }_2}3}}\) \( = {\left( {{3^{{{\log }_3}2}}} \right)^4} - {\left( {{2^{{{\log }_2}3}}} \right)^3}\) \( = {2^4} - {3^3} =  - 11\)

Chọn A.

Câu 8 (TH)

Phương pháp:

Thể tích lăng trụ \(V = Sh\) với \(S\) là diện tích đáy, \(h\) là chiều cao.

Cách giải:

Diện tích đáy \(S = \dfrac{{{a^2}\sqrt 3 }}{4}\)

Thể tích \(V = Sh = \dfrac{{{a^2}\sqrt 3 }}{4}.a = \dfrac{{{a^3}\sqrt 3 }}{4}\).

Chọn B.

Câu 9 (NB)

Phương pháp:

Thể tích khối chóp \(V = \dfrac{1}{3}Bh\)

Cách giải:

Thể tích khối chóp \(V = \dfrac{1}{3}Bh\)

Chọn C.

Câu 10 (TH)

Phương pháp:

- Tính đạo hàm \(y'\) và tìm nghiệm.

- Xét dấu \(y'\) và tìm khoảng nghịch biến (khoảng làm cho \(y' < 0\))

Cách giải:

Ta có: \(y' = 3{x^2} - 3 = 3\left( {{x^2} - 1} \right)\)

\(y' = 0 \Leftrightarrow x =  \pm 1\)

\(y' < 0 \Leftrightarrow  - 1 < x < 1\) nên hàm số nghịch biến trên \(\left( { - 1;1} \right)\).

Chọn C.

Câu 11 (NB)

Phương pháp:

Quan sát đồ thị và nhận xét dáng đồ thị, điểm đi qua và đối chiếu các đáp án.

Cách giải:

Từ đồ thị ta thấy đây là đồ thị hàm bậc bốn trùng phương có hệ số \(a > 0\), loại A, D.

Đồ thị hàm số đi qua điểm \(\left( {0;3} \right)\) nên chỉ có đáp án B thỏa mãn.

Chọn B.

Câu 12 (NB)

Phương pháp:

Khoảng làm cho \(y' < 0\) là khoảng nghịch biến của hàm số.

Cách giải:

Từ BBT ta thấy \(f'\left( x \right) < 0 \Leftrightarrow \left[ \begin{array}{l}x <  - 2\\x > 3\end{array} \right.\)

Do đó hàm số nghịch biến trên \(\left( { - \infty ; - 2} \right)\) và \(\left( {3; + \infty } \right)\).

Chọn C.

PHẦN II: TỰ LUẬN (7 điểm)

Câu 13 (VD)

Phương pháp:

- Tính \(y'\), tìm nghiệm.

- Tìm tọa độ các điểm cực trị và tính khoảng cách.

Cách giải:

Có \(y' = 3{x^2} + 6x,y' = 0\) \( \Leftrightarrow \left[ \begin{array}{l}x = 0 \Rightarrow y =  - 4\\x =  - 2 \Rightarrow y = 0\end{array} \right.\)

Đồ thị hàm số có hai điểm cực trị là \(A\left( {0; - 4} \right),\,\,B\left( { - 2;0} \right).\)

Độ dài \(AB = \sqrt {{{\left( { - 2} \right)}^2} + {4^2}}  = 2\sqrt 5 .\)

Câu 14 (TH)

Phương pháp:

Sử dụng các công thức \({a^m}.{a^n} = {a^{m + n}},{a^m}:{a^n} = {a^{m - n}}\) và \({\left( {{a^m}} \right)^n} = {a^{mn}}\).

Cách giải:

\(P = \dfrac{{{a^{\sqrt 3  + 1}}.{a^{2 - \sqrt 3 }}}}{{{{\left( {{a^{\sqrt 2  - 2}}} \right)}^{\sqrt 2  + 2}}}} = \dfrac{{{a^{\sqrt 3  + 1 + 2 - \sqrt 3 }}}}{{{a^{\left( {\sqrt 2  - 2} \right)\left( {\sqrt 2  + 2} \right)}}}}\)

\(P = \dfrac{{{a^3}}}{{{a^{2 - 4}}}} = {a^5}.\)

Câu 15 (VD)

Phương pháp:

- Tìm giao điểm của \(\left( P \right)\) với trục tung.

- Phương trình tiếp tuyến \(y = f'\left( {{x_0}} \right)\left( {x - {x_0}} \right) + f\left( {{x_0}} \right)\).

Cách giải:

Cho \(x = 0 \Rightarrow y =  - 3\) nên \(\left( C \right)\) cắt \(Oy\) tại \(A\left( {0; - 3} \right).\)

Có \(y' = \dfrac{5}{{{{\left( {x + 1} \right)}^2}}} \Rightarrow y'\left( 0 \right) = 5.\)

Phương trình tiếp tuyến của \(\left( C \right)\) tại \(A\) là \(y = 5x - 3\).

Câu 16 (VD):

Phương pháp:

- Xét phương trình hoành độ giao điểm.

- Tìm điều kiện của tham số để phương trình có ba nghiệm phân biệt bằng phương pháp hàm số.

Cách giải:

Xét phương trình hoành độ giao điểm \({x^3} + 2{x^2} - 2 = 7x + m\) \( \Leftrightarrow {x^3} + 2{x^2} - 7x - 2 = m\)

Xét hàm số \(f\left( x \right) = {x^3} + 2{x^2} - 7x - 2,\) có \(f'\left( x \right) = 3{x^2} + 4x - 7\)

\(f'\left( x \right) = 0 \Leftrightarrow \left[ \begin{array}{l}x = 1\\x =  - \dfrac{7}{3}\end{array} \right.\)

BBT

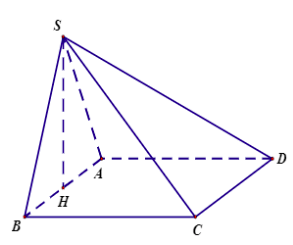
Từ BBT suy ra để phương trình đã cho có ba nghiệm phân biệt thì \( - 6 < m < \dfrac{{338}}{{27}}\).

Câu 17 (VD)

Phương pháp:

Thể tích lăng trụ \(V = Sh\) với \(S\) là diện tích đáy, \(h\) là chiều cao.

Cách giải:

Ta có \(AB = 1,AC = 2\) \( \Rightarrow BC = \sqrt {A{C^2} - A{B^2}}  = \sqrt 3 .\)

Vậy \({S_{ABC}} = \dfrac{1}{2}BA.BC = \dfrac{{\sqrt 3 }}{2}\)

\(BH = \dfrac{{BA.BC}}{{AC}} = \dfrac{{1.\sqrt 3 }}{2} = \dfrac{{\sqrt 3 }}{2}.\)

\(B'H = \sqrt {BB{'^2} - B{H^2}}  = \sqrt {5 - \dfrac{3}{4}}  = \dfrac{{\sqrt {17} }}{2}.\)

Do đó \({V_{ABC.A'B'C'}} = B'H.{S_{ABC}}\) \( = \dfrac{{\sqrt {17} }}{2} \cdot \dfrac{{\sqrt 3 }}{2} = \dfrac{{\sqrt {51} }}{4}.\)

Câu 18 (VD):

Phương pháp:

Gọi \(H\) là trung điểm \(AB\), chứng minh \(SH \bot \left( {ABCD} \right)\).

Thể tích hình chóp \(V = \dfrac{1}{3}Sh\).

Cách giải:

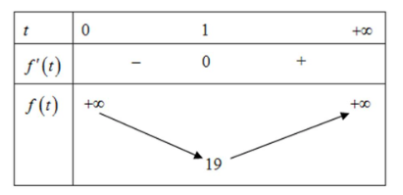
Gọi \(H\) là trung điểm \(AB\) \( \Rightarrow SH \bot \left( {ABCD} \right).\)

Do \(SAB\) đều cạnh \(a\) nên \(SH = \dfrac{{a\sqrt 3 }}{2}.\)

Diện tích đáy \({S_{ABCD}} = {a^2}\)

Thể tích khối chóp cần tìm là \(V = \dfrac{1}{3}SH.{S_{ABCD}}\)  \( = \dfrac{1}{3} \cdot \dfrac{{a\sqrt 3 }}{2} \cdot {a^2} = \dfrac{{\sqrt 3 {a^3}}}{6}.\)

Câu 19 (VDC):

Phương pháp:

Biến đổi biểu thức về chỉ xuất hiện \({\log _b}\dfrac{a}{b}\) và đặt \(t = {\log _{\dfrac{a}{b}}}b\).

Tìm GTNN bằng phương pháp hàm số và kết luận.

Cách giải:

Có \(P = \log _{\dfrac{a}{b}}^2\left( {ab} \right) + 12{\log _b}\left( {\dfrac{a}{b}} \right) - 2\) \( = {\left[ {{{\log }_{\dfrac{a}{b}}}\left( {\dfrac{a}{b} \cdot {b^2}} \right)} \right]^2} + 12{\log _b}\left( {\dfrac{a}{b}} \right) - 2\)

\( = {\left( {1 + 2{{\log }_{\dfrac{a}{b}}}b} \right)^2} + \dfrac{{12}}{{{{\log }_{\dfrac{a}{b}}}b}} - 2\)

Đặt \(t = {\log _{\dfrac{a}{b}}}b,\,t > 0\) do \(a > b > 1.\)

Khi đó, \(P = f\left( t \right) = {\left( {1 + 2t} \right)^2} + \dfrac{{12}}{t} - 2\) \( = 4{t^2} + 4t + \dfrac{{12}}{t} - 1\) với \(t > 0.\)

Có \(f'\left( t \right) = 8t + 4 - \dfrac{{12}}{{{t^2}}} = \dfrac{{8{t^3} + 4{t^2} - 12}}{{{t^2}}},\) \(f'\left( t \right) = 0 \Leftrightarrow t = 1.\)

BBT

Từ BBT suy ra giá trị nhỏ nhất của \(P\) là \(\min P = \mathop {\min }\limits_{\left( {0; + \infty } \right)} f\left( t \right) = 19.\)

Dấu “=” xảy ra khi \(t = 1 \Leftrightarrow {\log _{\dfrac{a}{b}}}b = 1\) \( \Leftrightarrow b = \dfrac{a}{b} \Leftrightarrow a = {b^2}\).

Loigiaihay.com