Giải đề thi giữa học kì 1 toán lớp 10 năm 2020 - 2021 trường THCS & THPT Nguyễn Tất Thành

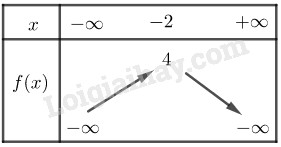
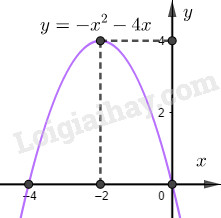
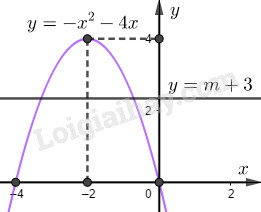
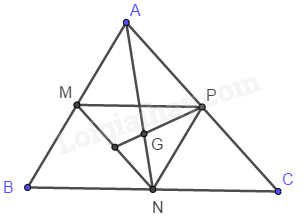
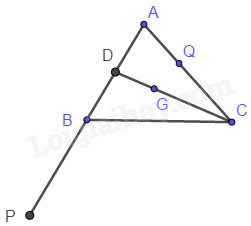
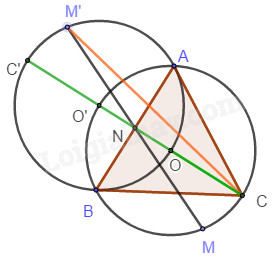
Đề bài

Câu 1. (2 điểm)

1) Tìm tập xác định của hàm số $f\left( x \right) = \dfrac{{{x^2} - 3}}{{2{\rm{x}} - 3}} + 2\sqrt {2 - x}$

2) Cho tập hợp $A\left( { - 1;3} \right]$ và $B = \left( {m - 2;m + 3} \right]$. Tìm $m$ để $A \cap B = \emptyset$.

Câu 2. (2 điểm)

1) Tìm $m$ để hàm số $f(x) = 4mx + 3 - \left( {5 + 2m} \right)x$ đồng biến trên $\mathbb{R}$.

2) Xét tính chẵn lẻ của hàm số $f\left( x \right) = 2{x^4} - 5x + 3$.

Câu 3. (2 điểm)

1) Lập bảng biến thiên và vẽ đồ thị hàm số $y =  - {x^2} - 4x$

2) Tìm $m$ để phương trình $- {x^2} - 4{\rm{x}} = m + 3$ có 2 nghiệm âm phân biệt.

Câu 4. (2 điểm)

Trong mặt phẳng $Oxy$ cho $M\left( {3; - 1} \right),N\left( {1;2} \right),P\left( {2; - 4} \right)$.

1) Tìm tọa độ trọng tâm G của tam giác $MNP$ và tọa độ điểm $D$ sao cho $MNGD$ là hình bình hành.

2) Tam giác $ABC$ nhận $M,N,P$ lần lượt là trung điểm của các cạnh $AB,BC,AC$. Tính tọa độ các điểm $A,B,C$.

Câu 5. (1 điểm)

Tìm a, b, c để đồ thị hàm số $y = a{x^2} + bx + c$ là đường Parabol có đỉnh $I\left( {2; - 2} \right)$ và đi qua điểm $A\left( {0;2} \right)$.

Câu 6. (1 điểm)

1) Cho tam giác $ABC$ có trọng tâm G và hai điểm $P,Q$ thỏa mãn $\overrightarrow {PA}  = 2\overrightarrow {PB}$, $3\overrightarrow {QA}  =  - 2\overrightarrow {QC}$. Chứng minh rằng ba điểm $P,Q,G$ thẳng hàng.

2) Cho tam giác $ABC$ đều cạnh a nội tiếp đường tròn $\left( O \right)$. Điểm $M$ thuộc $\left( O \right)$. Tìm giá trị lớn nhất, nhỏ nhất của $\left| {\overrightarrow {MA}  + \overrightarrow {MB}  - \overrightarrow {MC} } \right|$

Lời giải chi tiết

Câu 1. (VD)

1) Tìm tập xác định của hàm số $f\left( x \right) = \dfrac{{{x^2} - 3}}{{2{\rm{x}} - 3}} + 2\sqrt {2 - x}$

2) Cho tập hợp $A\left( { - 1;3} \right]$ và $B = \left( {m - 2;m + 3} \right]$. Tìm $m$ để $A \cap B = \emptyset$.

Phương pháp

1) Hàm $y = \dfrac{1}{{\sqrt {f\left( x \right)} }}$ xác định khi và chỉ khi $f\left( x \right) > 0$.

Hàm $y = \sqrt {f\left( x \right)}$ xác định khi và chỉ khi $f\left( x \right) \ge 0$.

2) Hai tập số trong $\mathbb{R}$ được gọi là giao bằng rỗng nếu chúng rời nhau trên $\mathbb{R}$.

Cách giải

1) Điều kiện xác định:

$\left\{ \begin{array}{l}2{\rm{x}} - 3 > 0\\2 - x \ge 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x > \dfrac{3}{2}\\x \le 2\end{array} \right.$

$\Rightarrow$Tập xác định: $D = \left( {\dfrac{3}{2};2} \right]$

2) $A \cap B = \emptyset  \Leftrightarrow \left[ \begin{array}{l}m - 2 \ge 3\\m + 3 \le  - 1\end{array} \right.$$\Leftrightarrow \left[ \begin{array}{l}m \ge 5\\m \le  - 4\end{array} \right.$

Câu 2. (TH)

1) Tìm $m$ để hàm số $f(x) = 4mx + 3 - \left( {5 + 2m} \right)x$ đồng biến trên $\mathbb{R}$.

2) Xét tính chẵn lẻ của hàm số $f\left( x \right) = 2{x^4} - 5x + 3$.

Phương pháp

1) Hàm số $y = ax + b$ đồng biến trên $R$ khi và chỉ khi $a > 0$.

2) Các bước xét tính chẵn- lẻ của hàm số $y = f\left( x \right)$

B1: Tìm tập xác định $D$ của hàm số.

B2: Kiểm tra điều kiện $- x \in D\forall x \in D$

B3: Kiểm tra điều kiện:

Nếu $f\left( { - x} \right) = f\left( x \right)\forall x \in D$ thì $f\left( x \right)$ là hàm số chẵn.

Nếu $f\left( { - x} \right) =  - f\left( x \right)\forall x \in D$ thì $f\left( x \right)$ là hàm số lẻ.

Nếu $\exists x \in D:$$f\left( { - x} \right) \ne  \pm f\left( x \right)$  thì hàm số không chẵn không lẻ.

Cách giải

1) Ta có:

$\begin{array}{l}f\left( x \right) = 4mx + 3 - \left( {5 + 2m} \right)x\\ = \left( {2m - 5} \right)x + 3\end{array}$

$f\left( x \right)$ đồng biến trên $R$ khi và chỉ khi $2m - 5 > 0 \Leftrightarrow m > \dfrac{5}{2}$

2) TXĐ: $D = R$

Ta có: $- x \in R\forall x \in R$

$\begin{array}{l}f\left( { - x} \right) = 2{\left( { - x} \right)^4} - 5\left( { - x} \right) + 3\\ = 2{x^4} + 5x + 3 \ne  \pm f\left( x \right)\end{array}$

Do đó hàm số không chẵn, không lẻ.

Câu 3. (VD)

1) Lập bảng biến thiên và vẽ đồ thị hàm số $y =  - {x^2} - 4x$

2) Tìm $m$ để phương trình $- {x^2} - 4x = m + 3$ có 2 nghiệm âm phân biệt.

Phương pháp

1) Hàm số $y = a{x^2} + bx + c\left( {a \ne 0} \right)$ có đỉnh $I\left( { - \dfrac{b}{{2{\rm{a}}}}; - \dfrac{\Delta }{{4{\rm{a}}}}} \right)$ nhận trục $x =  - \dfrac{b}{{2{\rm{a}}}}$ làm trục đối xứng.

Nếu $a > 0$ thì hàm số đồng biến trên $\left( { - \dfrac{b}{{2{\rm{a}}}}; + \infty } \right)$, nghịch biến trên $\left( { - \infty ; - \dfrac{b}{{2{\rm{a}}}}} \right)$ và đồ thị có bề lõm hướng lên trên.

Nếu $a < 0$ thì hàm số đồng biến trên $\left( { - \infty ; - \dfrac{b}{{2{\rm{a}}}}} \right)$, nghịch biến trên  $\left( { - \dfrac{b}{{2{\rm{a}}}}; + \infty } \right)$ và đồ thị có bề lõm hướng xuống dưới.

2) Nghiệm của phương trình $f\left( x \right) = g\left( x \right)$ là hoành độ các giao điểm của hai đồ thị hàm số $y = f\left( x \right)$ và $y = g\left( x \right)$.

Cách giải

1) Ta có: $a =  - 1 < 0$,  $- \dfrac{b}{{2{\rm{a}}}} =  - 2$  và $- \dfrac{\Delta }{{4{\rm{a}}}} = 4$.

$\Rightarrow$Hàm số đồng biến trên $\left( { - \infty ; - 2} \right)$ và nghịch biến trên $\left( { - 2; + \infty } \right)$.

Bảng biến thiên:

$a =  - 1 < 0$, bề lõm hướng xuống dưới.

Đồ thị có đỉnh $I\left( { - 2;4} \right)$, nhận đường thẳng $x =  - 2$ làm trục đối xứng.

Đồ thị đi qua điểm $O\left( {0;0} \right),A\left( { - 4;0} \right)$

Đồ thị:

2) Hoành độ giao điểm của đồ thị $y = f\left( x \right)$ và đường thẳng $y = m + 3$ là nghiệm của phương trình $- {x^2} - 4x = m + 3$.

Do đó phương trình $- {x^2} - 4x = m + 3$ có 2 nghiệm âm phân biệt khi và chỉ khi đường thẳng $y = m + 3$ cắt đồ thị tại 2 điểm có hoành độ âm phân biệt.

Từ đồ thị ta có đường thẳng $y = m + 3$ cắt đồ thị tại 2 điểm có hoành độ âm phân biệt khi và chỉ khi $0 < m + 3 < 4 \Leftrightarrow  - 3 < m < 1$.

Vậy $- 3 < m < 1$.

Câu 4. (VD)

Trong mặt phẳng $Oxy$ cho $M\left( {3; - 1} \right),N\left( {1;2} \right),P\left( {2; - 4} \right)$.

1) Tìm tọa độ trọng tâm G của tam giác $MNP$ và tọa độ điểm $D$ sao cho $MNGD$ là hình bình hành.

2) Tam giác $ABC$ nhận $M,N,P$ lần lượt là trung điểm của các cạnh $AB,BC,AC$. Tính tọa độ các điểm $A,B,C$.

Phương pháp

1) Trọng tâm G của tam giác MNP là $\left\{ \begin{array}{l}{x_G} = \dfrac{{{x_M} + {x_N} + {x_P}}}{3}\\{y_G} = \dfrac{{{y_M} + {y_N} + {y_P}}}{3}\end{array} \right.$

$MNGD \Leftrightarrow \overrightarrow {MN}  = \overrightarrow {DG}$

2) Sử dụng tính chất trung điểm $M$ là trung điểm của $AB$$\Rightarrow \overrightarrow {AM}  = \overrightarrow {MB}$.

Hiệu của hai vectơ: $\overrightarrow {AB}  - \overrightarrow {AC}  = \overrightarrow {CB}$.

Cách giải

1) Trọng tâm G của tam giác MNP nên tọa độ của G là:

 $\left\{ \begin{array}{l}{x_G} = \dfrac{{{x_M} + {x_N} + {x_P}}}{3} = 2\\{y_G} = \dfrac{{{y_M} + {y_N} + {y_P}}}{3} =  - 1\end{array} \right.$

$\begin{array}{l}MNGD \Leftrightarrow \overrightarrow {MN}  = \overrightarrow {DG} \\ \Leftrightarrow \left\{ \begin{array}{l}{x_D} = {x_G} - {x_N} + {x_M} = 4\\{y_D} = {y_G} - {y_N} + {y_M} =  - 4\end{array} \right.\\ \Rightarrow D\left( {4; - 4} \right)\end{array}$

2) $M,N,P$ lần lượt là trung điểm của $AB,BC,AC$

$\Rightarrow \left\{ \begin{array}{l}\overrightarrow {AM}  = \overrightarrow {MB}  = \dfrac{1}{2}\overrightarrow {AB} \\\overrightarrow {BN}  = \overrightarrow {NC}  = \dfrac{1}{2}\overrightarrow {BC} \\\overrightarrow {AP}  = \overrightarrow {PC}  = \dfrac{1}{2}\overrightarrow {AC} \end{array} \right.$$\Rightarrow \overrightarrow {MP}  = \dfrac{1}{2}\left( {\overrightarrow {AC}  - \overrightarrow {AB} } \right) = \overrightarrow {BN}$

$\Rightarrow \left\{ \begin{array}{l}{x_B} = {x_N} + {x_M} - {x_P} = 2\\{y_B} = {y_N} + {y_M} - {y_P} = 5\end{array} \right.$

M là trung điểm của AB nên $\left\{ \begin{array}{l}{x_A} = 2{{\rm{x}}_M} - {x_B}\\{y_A} = 2{y_M} - {y_B}\end{array} \right. \Rightarrow A\left( {4; - 7} \right)$

N là trung điểm của BC nên $\left\{ \begin{array}{l}{x_C} = 2{{\rm{x}}_N} - {x_B}\\{y_C} = 2{y_N} - {y_B}\end{array} \right. \Rightarrow C\left( {0; - 1} \right)$

Vậy $A\left( {4; - 7} \right),B\left( {2;5} \right),C\left( {0; - 1} \right)$.

Câu 5. (VD)

Tìm a, b, c để đồ thị hàm số $y = a{x^2} + bx + c$ là đường Parabol có đỉnh $I\left( {2; - 2} \right)$ và đi qua điểm $A\left( {0;2} \right)$.

Phương pháp

Đồ thị hàm số $y = a{x^2} + bx + c$ có đỉnh $I\left( { - \dfrac{b}{{2{\rm{a}}}}; - \dfrac{\Delta }{{4{\rm{a}}}}} \right)$.

$A\left( {{x_0};{y_0}} \right)$ thuộc đồ thị $\Leftrightarrow {y_0} = a{x_0} + b{x_0} + c$.

Cách giải

Đồ thị hàm số $y = a{x^2} + bx + c$ có đỉnh $I\left( { - \dfrac{b}{{2{\rm{a}}}}; - \dfrac{\Delta }{{4{\rm{a}}}}} \right)$ nên ta có:

$\left\{ \begin{array}{l} - \dfrac{b}{{2{\rm{a}}}} = 2\\ - 2 = a{.2^2} + b.2 + c\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}b =  - 4{\rm{a}}\\4{\rm{a}} + 2b + c =  - 2\end{array} \right.\left( 1 \right)$

$A\left( {0;2} \right)$ thuộc đồ thị nên $c = 2$. Thay vào (1) ta được:

$\left\{ \begin{array}{l}b + 4{\rm{a}} = 0\\4{\rm{a}} + 2b =  - 4\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = 1\\b =  - 4\end{array} \right.$.

Vậy $a = 1,b =  - 4,c = 2$

Câu 6. (VDC)

1) Cho tam giác $ABC$ có trọng tâm G và hai điểm $P,Q$ thỏa mãn $\overrightarrow {PA}  = 2\overrightarrow {PB}$, $3\overrightarrow {QA}  =  - 2\overrightarrow {QC}$. Cứng minh rằng ba điểm $P,Q,G$ thẳng hàng.

2) Cho tam giác $ABC$ đều cạnh a nội tiếp đường tròn $\left( O \right)$. Điểm $M$ thuộc $\left( O \right)$. Tìm giá trị lớn nhất, nhỏ nhất của $\left| {\overrightarrow {MA}  + \overrightarrow {MB}  - \overrightarrow {MC} } \right|$

Phương pháp

1) P, Q, G thẳng hàng khi và chỉ khi $\exists k \ne 0:\overrightarrow {PG}  = k\overrightarrow {PQ}$.

2)

B1: Gọi N là trung điểm của AB, O’ là điểm đối xứng O qua N, M' đối xứng M qua N.

B2: Tìm quỹ tích điểm M’.

B3: $\left| {\overrightarrow {MA}  + \overrightarrow {MB}  - \overrightarrow {MC} } \right| = CM'$ . Đánh giá CM’ tìm giá trị lớn nhất, nhỏ nhất cần tìm.

Cách giải

1)

$\overrightarrow {PA}  = 2\overrightarrow {PB}  \Rightarrow \overrightarrow {AB}  = \overrightarrow {AP}  + \overrightarrow {PB}  = \dfrac{1}{2}\overrightarrow {AP}$

$\begin{array}{l}3\overrightarrow {QA}  =  - 2\overrightarrow {QC} \\ \Rightarrow \overrightarrow {AC}  = \overrightarrow {AQ}  + \overrightarrow {QC} \\ = \overrightarrow {AQ}  + \dfrac{3}{2}\overrightarrow {AQ}  = \dfrac{5}{2}\overrightarrow {AQ} \end{array}$

$\Rightarrow \overrightarrow {PQ}  = \overrightarrow {AQ}  - \overrightarrow {AP}  = \dfrac{2}{5}\overrightarrow {AC}  - 2\overrightarrow {AB}$

$\overrightarrow {PG}  = \overrightarrow {PA}  + \overrightarrow {AG}$

$\begin{array}{l} =  - 2\overrightarrow {AB}  + \dfrac{2}{3}.\dfrac{1}{2}\left( {\overrightarrow {AB}  + \overrightarrow {AC} } \right)\\ = \dfrac{1}{3}\overrightarrow {AC}  - \dfrac{5}{3}\overrightarrow {AB}  = \dfrac{5}{6}\left( {\dfrac{2}{5}\overrightarrow {AC}  - 2\overrightarrow {AB} } \right)\\ = \dfrac{5}{6}\overrightarrow {PQ} \end{array}$

Suy ra $\overrightarrow {PQ} ,\overrightarrow {PG}$ cùng phương. Hay P, Q, G thẳng hàng.

2)

Gọi N là trung điểm của AB, O’ là điểm đối xứng O qua N, M’ đối xứng M qua N. Khi đó:

$\begin{array}{l}\left| {\overrightarrow {MA}  + \overrightarrow {MB}  - \overrightarrow {MC} } \right| = \left| {2\overrightarrow {MN}  - \overrightarrow {MC} } \right|\\ = \left| {\overrightarrow {MM'}  - \overrightarrow {MC} } \right| = \left| {\overrightarrow {CM'} } \right| = CM'\end{array}$

Ta có tam giác $ABC$ đều cạnh a nội tiếp đường tròn $\left( O \right)$ nên $\left( O \right)$ có bán kính $\dfrac{a}{{\sqrt 3 }}$.

Mặt khác, ta có: $\left\{ \begin{array}{l}\overrightarrow {O'N}  = \overrightarrow {NO} \\\overrightarrow {M'N}  = \overrightarrow {NM} \end{array} \right. \Rightarrow \overrightarrow {O'M'}  = \overrightarrow {MO}$

$\Rightarrow O'M' = \dfrac{a}{{\sqrt 3 }}$.

Do O, N cố định nên M’ luôn thuộc đường tròn tâm O’, bán kính $\dfrac{a}{{\sqrt 3 }}$.

$\Rightarrow CO \le CM' \le CC'$ (C’ đối xứng C qua N).

$\Rightarrow \min \left( {\left| {\overrightarrow {MA}  + \overrightarrow {MB}  - \overrightarrow {MC} } \right|} \right) = a$ khi $CM' = a = CO \Leftrightarrow M' \equiv O$. Suy ra O là điểm đối xứng M qua N. Hay M, C, O thẳng hàng.

$\begin{array}{l}\max \left( {\left| {\overrightarrow {MA}  + \overrightarrow {MB}  - \overrightarrow {MC} } \right|} \right) = CC'\\ = 2CN = 2.\dfrac{{a\sqrt 3 }}{2} = a\sqrt 3 \\ \Leftrightarrow C' \equiv M' \Leftrightarrow C \equiv M\end{array}$

 Loigiaihay.com