Giải câu hỏi trắc nghiệm trang 96 vở thực hành Toán 8 tập 2Chọn phương án đúng trong mỗi câu sau. Quảng cáo
Lựa chọn câu để xem lời giải nhanh hơn
Chọn phương án đúng trong mỗi câu sau. Câu 1 trang 96 Khẳng định nào dưới đây là đúng? A. Hai tam giác vuông có tổng hai góc nhọn bằng nhau thì đồng dạng với nhau. B. Hai tam giác vuông có một cặp cạnh bằng nhau thì đồng dạng với nhau. C. Hai tam giác vuông có diện tích bằng nhau thì đồng dạng với nhau. D. Hai tam giác vuông có một cặp góc nhọn bằng nhau thì đồng dạng với nhau. Phương pháp giải: Dựa vào các trường hợp đồng dạng của hai tam giác vuông. Lời giải chi tiết: Theo định lí 1: Nếu một góc nhọn của tam giác vuông này bằng một góc nhọn của tam giác vuông kia thì hai tam giác vuông đó đồng dạng với nhau. => Chọn đáp án D. Câu 2 trang 96 Cho tam giác ABC vuông tại A và tam giác DEF vuông tại D. Điều kiện nào dưới đây không suy ra $\Delta ABC\backsim \Delta DEF$? A. $\widehat{B}=\widehat{E}$. B. $\frac{AB}{DE}=\frac{AC}{DF}$. C. $\frac{AB}{DE}=\frac{BC}{EF}$. D. $\widehat{C}=\widehat{E}$. Phương pháp giải: Dựa vào các điều kiện để hai tam giác vuông đồng dạng với nhau. Lời giải chi tiết: Để tam giác $\Delta ABC\backsim \Delta DEF$ đồng dạng thì TH1. $\widehat{B}=\widehat{E}$ hoặc $\widehat{C}=\widehat{F}$. TH2. $\frac{AB}{DE}=\frac{AC}{DF}$. TH3. $\frac{AB}{DE}=\frac{BC}{EF}$. => Chọn đáp án D. Câu 3 trang 96 Cho tam giác ABC vuông tại A và có đường cao AH. Khẳng định nào sau đây là đúng? A. $\Delta ABC\backsim \Delta HAB$. B. $\Delta ABC\backsim \Delta HCA$. C. $\Delta HAB\backsim \Delta HAC$. D. $\Delta ACB\backsim \Delta HCA$. Phương pháp giải: Dựa vào các trường hợp đồng dạng của hai tam giác vuông. Lời giải chi tiết:
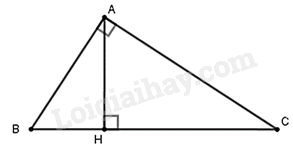
Xét tam giác $\Delta ACB\backsim \Delta HCA$ có: $\widehat{A}=\widehat{H}={{90}^{0}}$ $\widehat{C}$ chung => Tam giác $\Delta ACB\backsim \Delta HCA$. => Chọn đáp án D.
|




















Danh sách bình luận