Bài 51 trang 120 Vở bài tập toán 9 tập 2

Đề bài

a) Vẽ hình 58 (tạo bởi các cung tròn) với \(HI = 10 cm\) và \(HO = HI = 2cm\). Nêu cách vẽ:

b) Tính diện tích hình HOABINH (miền gạch chéo).

c) Chứng tỏ rằng hình tròn đường kính NA có cùng diện tích với hình HOABINH đó.

Lời giải chi tiết

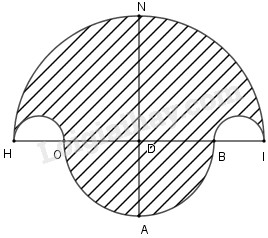
a) Cách vẽ : 

- Vẽ đoạn thẳng \(HI = 10cm\). 

- Vẽ đường trung trực \(d\) của \(HI\). Gọi \(D\) là giao điểm của \(d\) với \(HI.\)

- Lấy \(D\) làm tâm vẽ cung tròn với bán kính \(\dfrac{{HI}}{2} = \dfrac{{10}}{2} = 5cm,\) cắt \(d\) tại \(N\) và \(A.\)

- Lấy \(D\) làm tâm vẽ cung tròn với bán kính \(DB = 3cm\) về phía đối diện cung \(HNI,\) cắt \(HI\) tại \(O\) và \(B.\)

- Lấy điểm chính giữa của \(HO\) làm tâm, vẽ cung tròn với bán kính bằng \(1cm.\)

- Lấy điểm chính giữa của \(BI\) làm tâm, vẽ cung tròn với bán kính bằng \(1cm.\)

b) Tính diện tích của hình gạch chéo :

Vì hình gạch chéo được tạo bởi các nửa đường tròn bán kính \(5cm;3cm\) và \(1cm.\)

Ta có : \({S_{HOABINH}} = {S_{HNIBO}} + {S_{BAO}};\)   (1)

             \({S_{HNIBO}} = {S_{HNI}} - 2{S_{OH}}.\)

(\({S_{OH}} = {S_{BI}}\) là diện tích nửa hình tròn đường kính \(OH = IB = 2cm).\)

\({S_{HNI}} = \dfrac{1}{2}\pi .D{H^2}\) và \(2{S_{OH}} = \pi {\left( {\dfrac{{HO}}{2}} \right)^2}\) \( \Rightarrow {S_{HNIBO}} = \dfrac{1}{2}\pi O{H^2} - \pi {\left( {\dfrac{{HO}}{2}} \right)^2}\)\( = \dfrac{{23\pi }}{2}\)       (2)  

\({S_{BAO}} = \dfrac{1}{2}\pi D{O^2} = \dfrac{{9\pi }}{2}\,\left( {c{m^2}} \right)\)                                                                                      (3) 

Thay kết quả từ (2) và (3) vào (1), ta được \({S_{HOABINH}} = \dfrac{{9\pi }}{2} + \dfrac{{23\pi }}{2} = 16\pi \left( {c{m^2}} \right)\)

c) Gọi \(S\) là diện tích hình tròn đường kính \(NA;R\) là bán kính.

Ta có : \(NA = ND + DA = 5 + 3 = 8\left( {cm} \right).\) Bán kính \(R = \dfrac{1}{2} \cdot 8 = 4cm.\)  

\(S = \pi {R^2} = \pi {.4^2} = 16\pi \left( {c{m^2}} \right).\)

Vậy \({S_{HOABINH}} = S\)_{đường tròn đường kính NA}   (đpcm).

Loigiaihay.com