Trang chủ

Giải chuyên đề học tập Toán lớp 11 Chân trời sáng tạo

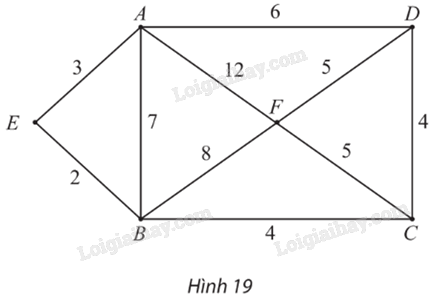
Giải bài 5 trang 66 Chuyên đề học tập Toán 11 Chân trời sáng tạo

Tìm đường đi ngắn nhất từ đỉnh A đến từng đỉnh (khác A) trong đồ thị có trọng số ở Hình 19.

Quảng cáo

Đề bài

Tìm đường đi ngắn nhất từ đỉnh A đến từng đỉnh (khác A) trong đồ thị có trọng số ở Hình 19.

Phương pháp giải - Xem chi tiết

Thuật toán tìm đường đi ngắn nhất từ đỉnh A đến đỉnh T

Mở đầu: Gán nhãn của A bằng 0, các đỉnh khác bằng \(\infty \). Khoanh tròn đỉnh A.

Các bước lặp

Trong mỗi bước lặp thực hiện các thao tác sau đây:

- Gọi U là đỉnh vừa được khoanh tròn ở bước trước. Trong các đỉnh chưa khoanh tròn, xét lần lượt từng đỉnh V kề với đỉnh U, tính \({n_U}\; + {\rm{ }}{w_{UV}}\), rồi so sánh số này với nhãn hiện tại \({n_V}\;\) của V. Nếu số đó nhỏ hơn thì đổi nhãn \({n_V}\;\) bằng số đó.

- So sánh nhãn của tất cả các đỉnh chưa khoanh tròn. Đỉnh nào có nhãn nhỏ nhất thì khoanh tròn đỉnh đó (nếu có nhiều đỉnh hư vậy thì khoanh một đỉnh tùy ý trong số đó).

- Nếu đỉnh T chưa được khoanh tròn thì thực hiện bước lặp tiếp theo, trái lại thì kết thức các bước lặp.

Kết luận: Dò lại các bước lặp để viết được nhãn \({n_T}\) của T dưới dạng tổng độ dài các cạnh. Từ đó nhận được đường đi ngắn nhất từ A đến T cùng với độ dài của nó.

Lời giải chi tiết

– Gán nhãn cho A bằng 0 (tức là, \({n_A}\; = {\rm{ }}0\)), các đỉnh khác bằng \(\infty \). Khoanh tròn đỉnh A.

– Tại các đỉnh kề với A, gồm E, B, D, F, ta có:

⦁ \({n_E}\; = {\rm{ }}{n_A}\; + {\rm{ }}{w_{AE}}\; = {\rm{ }}0{\rm{ }} + {\rm{ }}3{\rm{ }} = {\rm{ }}3\).Vì \(3{\rm{ }} < {\rm{ }}\infty \) nên ta đổi nhãn của E thành 3.

⦁ \({n_B}\; = {\rm{ }}{n_A}\; + {\rm{ }}{w_{AB}}\; = {\rm{ }}0{\rm{ }} + {\rm{ }}7{\rm{ }} = {\rm{ }}7\).Vì \(7{\rm{ }} < {\rm{ }}\infty \) nên ta đổi nhãn của B thành 7.

⦁ \({n_D}\; = {\rm{ }}{n_A}\; + {\rm{ }}{w_{AD}}\; = {\rm{ }}0{\rm{ }} + {\rm{ }}6{\rm{ }} = {\rm{ }}6\).Vì \(6{\rm{ }} < {\rm{ }}\infty \) nên ta đổi nhãn của D thành 6.

⦁ \({n_F}\; = {\rm{ }}{n_A}\; + {\rm{ }}{w_{AF}}\; = {\rm{ }}0{\rm{ }} + {\rm{ }}12{\rm{ }} = {\rm{ }}12\).Vì \(12{\rm{ }} < {\rm{ }}\infty \) nên ta đổi nhãn của F thành 12.

Trong các đỉnh chưa được khoanh tròn, đỉnh có nhãn bé nhất là E nên ta khoanh tròn đỉnh E (đỉnh gần A nhất, chỉ tính các đỉnh khác A).

Ta có \({n_E}\; = {\rm{ }}3{\rm{ }} = {\rm{ }}{n_A}\; + {\rm{ }}{w_{AE}}\; = {\rm{ }}{w_{AE}}\; = {\rm{ }}{l_{AE}}.\)

Vì vậy AE là đường đi ngắn nhất từ A đến E, với độ dài bằng 3.

– Trong các đỉnh chưa được khoanh tròn, đỉnh kề với đỉnh E chỉ có B, ta có:

\({n_B}\; = {\rm{ }}{n_E}\; + {\rm{ }}{w_{EB}}\; = {\rm{ }}3{\rm{ }} + {\rm{ }}2{\rm{ }} = {\rm{ }}5\).Vì \(5{\rm{ }} < {\rm{ }}7\) (7 là nhãn hiện tại của B) nên ta đổi nhãn của B thành 5.

Trong các đỉnh chưa được khoanh tròn, đỉnh có nhãn bé nhất là B nên ta khoanh tròn đỉnh B (đỉnh gần A thứ hai).

Ta có \({n_B}\; = {\rm{ }}5{\rm{ }} = {\rm{ }}{n_E}\; + {\rm{ }}{w_{EB}}\; = {\rm{ }}{n_A}\; + {\rm{ }}{w_{AE}}\; + {\rm{ }}{w_{EB}}\; = {\rm{ }}{w_{AE}}\; + {\rm{ }}{w_{EB}}\; = {\rm{ }}{l_{AEB}}.\)

Vì vậy AEB là đường đi ngắn nhất từ A đến B, với độ dài bằng 5.

– Trong các đỉnh chưa được khoanh tròn, đỉnh kề với đỉnh B gồm F, C, ta có:

\({n_F}\; = {\rm{ }}{n_B}\; + {\rm{ }}{w_{BF}}\; = {\rm{ }}5{\rm{ }} + {\rm{ }}8{\rm{ }} = {\rm{ }}13\).Vì \(13{\rm{ }} > {\rm{ }}12\) (12 là nhãn hiện tại của F) nên ta giữ nguyên nhãn của F là 12.

\({n_C}\; = {\rm{ }}{n_B}\; + {\rm{ }}{w_{BC}}\; = {\rm{ }}5{\rm{ }} + {\rm{ }}4{\rm{ }} = {\rm{ }}9.\)Vì \(9{\rm{ }} < {\rm{ }}\infty \) nên ta đổi nhãn của C thành 9.

Trong các đỉnh chưa được khoanh tròn, đỉnh có nhãn bé nhất là D nên ta khoanh tròn đỉnh D (đỉnh gần A thứ ba).

Ta có \({n_D}\; = {\rm{ }}6{\rm{ }} = {\rm{ }}{n_A}\; + {\rm{ }}{w_{AD}}\; = {\rm{ }}{w_{AD}}\; = {\rm{ }}{l_{AD}}.\)

Vì vậy AD là đường đi ngắn nhất từ đỉnh A đến D, với độ dài bằng 6.

– Trong các đỉnh chưa được khoanh tròn, đỉnh kề với đỉnh D gồm đỉnh F, C, ta có:

⦁ \({n_F}\; = {\rm{ }}{n_D}\; + {\rm{ }}{w_{DF}}\; = {\rm{ }}6{\rm{ }} + {\rm{ }}5{\rm{ }} = {\rm{ }}11.\)Vì \(11{\rm{ }} < {\rm{ }}12\) (12 là nhãn hiện tại của F) nên ta đổi nhãn của F thành 11.

⦁ \({n_C}\; = {\rm{ }}{n_D}\; + {\rm{ }}{w_{DC}}\; = {\rm{ }}6{\rm{ }} + {\rm{ }}4{\rm{ }} = {\rm{ }}10.\) Vì \(10{\rm{ }} > {\rm{ }}9\) (9 là nhãn hiện tại của C) nên ta giữ nguyên nhãn của C là 9.

Trong các đỉnh chưa được khoanh tròn, đỉnh có nhãn bé nhất là đỉnh C nên ta khoanh tròn đỉnh C (đỉnh gần A thứ tư).

Ta có \({n_C}\; = {\rm{ }}9{\rm{ }} = {\rm{ }}{n_B}\; + {\rm{ }}{w_{BC}}\)

\(\begin{array}{*{20}{l}}{ = {\rm{ }}{n_E}\; + {\rm{ }}{w_{EB}}\; + {\rm{ }}{w_{BC}}}\\{ = {\rm{ }}{n_A}\; + {\rm{ }}{w_{AE}}\; + {\rm{ }}{w_{EB}}\; + {\rm{ }}{w_{BC}}}\\{ = {\rm{ }}{w_{AE}}\; + {\rm{ }}{w_{EB}}\; + {\rm{ }}{w_{BC}}}\\{ = {\rm{ }}{l_{AEBC}}.}\end{array}\)

Vì vậy AEBC là đường đi ngắn nhất từ A đến C, với độ dài bằng 9.

– Lúc này, ta thấy chỉ còn đỉnh F chưa được khoanh tròn nên ta khoanh tròn đỉnh F (đỉnh gần A thứ năm).

Ta có \({n_F}\; = {\rm{ }}11{\rm{ }} = {\rm{ }}{n_D}\; + {\rm{ }}{w_{DF}}\; = {\rm{ }}{n_A}\; + {\rm{ }}{w_{AD}}\; + {\rm{ }}{w_{DF}}\; = {\rm{ }}{w_{AD}}\; + {\rm{ }}{w_{DF}}\; = {\rm{ }}{l_{ADF}}.\)

Vì vậy ADF là đường đi ngắn nhất từ A đến F, với độ dài bằng 11.

Vậy đường đi ngắn nhất từ đỉnh A đến các đỉnh B, C, D, E, F lần lượt là AEB, AEBC, AD, AE, ADF.