Giải bài 43 trang 45 sách bài tập toán 11 - Cánh diều

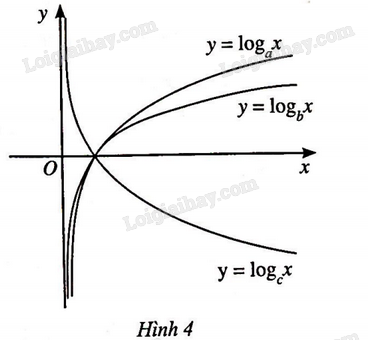
Đề bài

Cho ba số thực dương \(a,{\rm{ }}b,{\rm{ }}c\) khác 1 và đồ thị của ba hàm số loogarit \(y = {\log _a}x,\)\(y = {\log _b}x\) và \(y = {\log _c}x\) được cho bởi Hình  4. Kết luận nào sau đây là đúng đối với ba số\(a,{\rm{ }}b,{\rm{ }}c?\) 

A. \(c > b > a.\)

B. \(a > b > c.\)

C. \(b > a > c.\)

D. \(c > a > b.\)

Lời giải chi tiết

Hàm số lôgarit \(y = {\log _a}x\) và \(y = {\log _b}x\) đồng biến trên \(\left( {0; + \infty } \right) \Rightarrow a > 1;{\rm{ }}b > 1.\)

Hàm số lôgarit \(y = {\log _c}x\) nghịch biến trên \(\left( {0; + \infty } \right) \Rightarrow 0 < c < 1.\)

Thay \(x = 100 \Rightarrow {\log _a}100 > {\log _b}100 > 0 \Leftrightarrow \frac{1}{{{{\log }_{100}}a}} > \frac{1}{{{{\log }_{100}}b}}\)

\( \Leftrightarrow {\log _{100}}b > {\log _{100}}a \Leftrightarrow b > a > 1.\)

Vậy \(b > a > c.\)

Đáp án C.