Bài 23 trang 146 Vở bài tập toán 9 tập 2

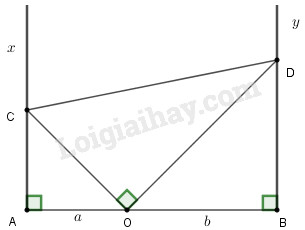
Đề bài

Cho ba điểm \(A, O, B\) thẳng hàng theo thứ tự đó, \(OA=a, OB=b\) (\(a, b\) cùng đơn vị: \(cm\)). Qua \(A\) và \(B\) vẽ theo thứ tự các tia \(Ax\) và \(By\) cùng vuông góc với \(AB\) và cùng phía với \(AB\). Qua \(O\) vẽ hai tia vuông góc với nhau và cắt \(Ax\) ở \(C, By\) ở \(D\) (xem hình 84)

a/ Chứng minh \(AOC\) và \(BDO\) là hai tam giác đồng dạng; từ đó suy ra tích \(AC.BD\) không đổi.

b/ Tính diện tích hình thang \(ABDC\) khi \(\widehat {COA} = 60^\circ\) 

 

c/ Với \(\widehat {COA} = 60^\circ \) cho hình vẽ quay quanh \(AB\). Hãy tính tỉ số thể tích các hình do các tam giác \(AOC\) và \(BOD\) tạo thành.

Lời giải chi tiết

a)  \(\Delta AOC\) và \(\Delta BDO\) là hai tam giác vuông vì \(A\,x \bot AB;By \bot AB.\)

Ta có \(\widehat {AOC} = \widehat {BDO}\) vì cùng phụ \(\widehat {BOD}.\)

Vậy \(\Delta AOC \backsim \Delta BDO\) vì có hai góc vuông và \(\widehat {AOC} = \widehat {BDO}\).

Từ đó ta có : \(\dfrac{{AC}}{{AO}} = \dfrac{{BO}}{{BD}} \Rightarrow AC.BD = AO.BO\)

Theo giả thiết \(AO = a;BO = b.\) 

Vậy \(AC.BD = ab\) hay tích \(AC.BD\) không đổi.

b) \({S_{ABCD}} = \dfrac{{AC + BD}}{2} \cdot AB\) mà \(h = AO + OB = a + b\)

Xét hai  tam giác vuông \(\Delta AOC\)và \(\Delta BOD.\)  Theo câu a) \( \Rightarrow \widehat {BOD} = \widehat {AOC} = 60^\circ .\)

Do đó,  ta có \(AC = AO.\tan 60^\circ  = a\sqrt 3 \) và  \(BD = \dfrac{{OB + AO}}{{AC}} = \dfrac{{b\sqrt 3 }}{3}\)

Vậy \({S_{ABCD}} = \dfrac{1}{2}\left( {a\sqrt 3  + \dfrac{{b\sqrt 3 }}{3}} \right)\left( {a + b} \right)\)\( = \dfrac{{\sqrt 3 }}{6}\left( {3{a^2} + 4ab + {b^2}} \right)\left( {c{m^2}} \right).\)

c) Nhận xét :

Các tam giác \(AOC\) và \(BOD\) khi quay quanh cạnh \(AB\) tạo thành hình nón  với các bán kính đáy lần lượt là \(AC,BD\) và đường cao lần lượt là \(AO,OB.\)

Gọi \({V_1},{V_2}\) là thể tích của hai hình nón.

 \({V_1} = \dfrac{1}{3}\pi .{r_1}^2.{h_1}\) và \({V_2} = \dfrac{1}{3}\pi {r_2}^2{h_{2.}}\)

Từ câu b) ta có : \(Ac = a\sqrt 3 ;BD = \dfrac{{b\sqrt 3 }}{3}\)  

Do đó  \(\dfrac{{{V_1}}}{{{V_2}}} = \dfrac{{\dfrac{1}{3}\pi {r_1}^2{h_1}}}{{\dfrac{1}{3}\pi {r_2}^2{h_2}}} = \dfrac{{3{a^2}.a}}{{\dfrac{{{b^2}}}{3} \cdot b}} = \dfrac{{9{a^3}}}{{{b^3}}}\)

Loigiaihay.com