Giải bài 128 trang 61 sách bài tập Toán 6 – Cánh Diều Tập 2Trong ba đợt tổng kết năm học tai một trường trung hoc cơ sở, tổng số học sinh giỏi của ba lớp 6A, 6B, 6C là 90 em. Biết rằng 2/5 số học sinh giỏi của lớp 6A bằng 1/3 số học sinh giỏi của lớp 6B và bằng 1/2 số học sinh giỏi của lớp 6C. Tính số học sinh giỏi của mỗi lớp. Quảng cáo
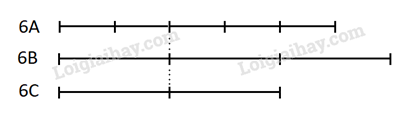
Đề bài Trong ba đợt tổng kết năm học tai một trường trung hoc cơ sở, tổng số học sinh giỏi của ba lớp 6A, 6B, 6C là 90 em. Biết rằng \(\frac{2}{5}\) số học sinh giỏi của lớp 6A bằng \(\frac{1}{3}\) số học sinh giỏi của lớp 6B và bằng \(\frac{1}{2}\) số học sinh giỏi của lớp 6C. Tính số học sinh giỏi của mỗi lớp. Phương pháp giải - Xem chi tiết Cách 1: Vẽ sơ đồ Cách 2: Tính tỉ số số học sinh giỏi của mỗi lớp so với số học giỏi của cả ba lớp Lời giải chi tiết Cách 1: Ta có sơ đồ: Dễ thấy: Nếu số học sinh giỏi của lớp 6A là 5 phần bằng nhau thì: Số học sinh giỏi của lớp 6B là 6 phần bằng nhau Số học sinh giỏi của lớp 6C là 4 phần bằng nhau Số học sinh giỏi của ba lớp là: \(5 + 6 + 4 = 15\) phần bằng nhau Mà số học sinh giỏi của ba lớp là 90 học sinh. Vậy số học sinh giỏi của lớp 6A là: \(90:15.5 = 30\)(học sinh) Số học sinh giỏi của lớp 6B là: \(90:15.6 = 36\)(học sinh) Số học sinh giỏi của lớp 6C là: \(90 - 30 - 36 = 24\) (học sinh) Cách 2: Vì \(\frac{2}{5}\) số học sinh giỏi của lớp 6A bằng \(\frac{1}{3}\) số học sinh giỏi của lớp 6B nên số học sinh giỏi của lớp 6B bằng: \(\frac{2}{5}.3 = \frac{6}{5}\)(số học sinh giỏi của lớp 6A) Vì \(\frac{2}{5}\) số học sinh giỏi của lớp 6A bằng \(\frac{1}{2}\) số học sinh giỏi của lớp 6C nên số học sinh giỏi của lớp 6C bằng: \(\frac{2}{5}.2 = \frac{4}{5}\)(số học sinh giỏi của lớp 6A) Vậy số học sinh giỏi của cả 3 lớp so với lớp 6A là: \(1 + \frac{6}{5} + \frac{4}{5} = 3\)( lần) Suy ra, số học sinh giỏi của lớp 6A là: \(90:3 = 30\)(học sinh) Số học sinh giỏi của lớp 6B là: \(\frac{6}{5}.30 = 36\)(học sinh) Số học sinh giỏi của lớp 6C là: \(\frac{4}{5}.30 = 24\) (học sinh)
|




















Danh sách bình luận