Giải bài 11 trang 96 sách bài tập toán 12 - Cánh diềuTrong mỗi ý a), b), c), d), chọn phương án đúng (Đ) hoặc sai (S). Một trung tâm ngoại ngữ thực hiện kiểm tra đầu vào của 80 học sinh đăng kí học, kết quả kiểm tra được cho bởi bảng tần số ghép nhóm như Bảng 17. a) Tổng số học sinh là 800. b) Số trung bình cộng của mẫu số liệu ghép nhóm đó là: 5,7875. c) Phương sai của mẫu số liệu ghép nhóm đó là: ({s^2} approx 3,85). d) Độ lệch chuẩn của mẫu số liệu ghép nhóm đó là: (s = sqrt {3,85} approx 1,962). Tổng hợp đề thi học kì 1 lớp 12 tất cả các môn - Cánh diều Toán - Văn - Anh - Lí - Hóa - Sinh - Sử - Địa Quảng cáo
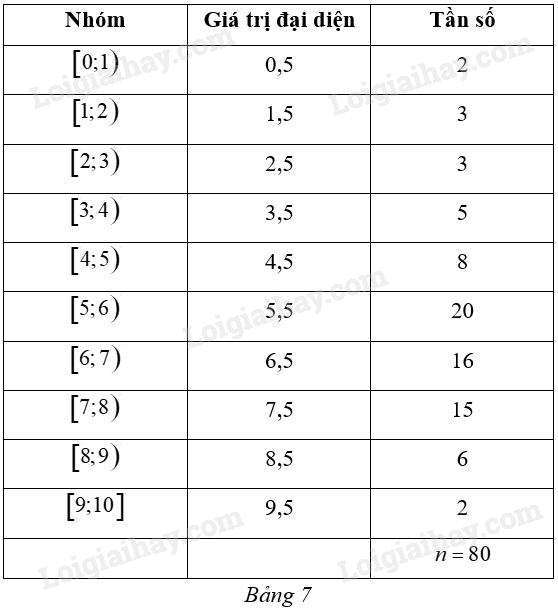
Đề bài Trong mỗi ý a), b), c), d), chọn phương án đúng (Đ) hoặc sai (S). Một trung tâm ngoại ngữ thực hiện kiểm tra đầu vào của 80 học sinh đăng kí học, kết quả kiểm tra được cho bởi bảng tần số ghép nhóm như Bảng 17.
a) Tổng số học sinh là 800. b) Số trung bình cộng của mẫu số liệu ghép nhóm đó là: 5,7875. c) Phương sai của mẫu số liệu ghép nhóm đó là: \({s^2} \approx 3,85\). d) Độ lệch chuẩn của mẫu số liệu ghép nhóm đó là: \(s = \sqrt {3,85} \approx 1,962\). Phương pháp giải - Xem chi tiết ‒ Sử dụng công thức tính số trung bình cộng của mẫu số liệu ghép nhóm: \(\overline x = \frac{{{m_1}{x_1} + ... + {m_k}{x_k}}}{n}\)trong đó \(n = {m_1} + ... + {m_k}\) là cỡ mẫu và \({x_i} = \frac{{{a_i} + {a_{i + 1}}}}{2}\) (với \(i = 1,...,k\)) là giá trị đại diện của nhóm \(\left[ {{a_i};{a_{i + 1}}} \right)\). ‒ Sử dụng công thức tính phương sai của mẫu số liệu ghép nhóm: \({s^2} = \frac{{{n_1}{{\left( {{x_1} - \overline x } \right)}^2} + {n_2}{{\left( {{x_2} - \overline x } \right)}^2} + ... + {n_m}{{\left( {{x_m} - \overline x } \right)}^2}}}{n}\) ‒ Sử dụng công thức tính độ lệch chuẩn của mẫu số liệu ghép nhóm: \(s = \sqrt {{s^2}} \). Lời giải chi tiết Tổng số học sinh là: \(n = 80\). Vậy a) sai. Số trung bình cộng của mẫu số liệu ghép nhóm ở Bảng 17 là: \(\overline x = \frac{{2.0,5 + 3.1,5 + 3.2,5 + 5.3,5 + 8.4,5 + 20.5,5 + 16.6,5 + 15.7,5 + 6.8,5 + 2.9,5}}{{80}} = \frac{{463}}{{80}} = 5,7875\) Vậy b) đúng. Phương sai của mẫu số liệu ghép nhóm đó là: \(\begin{array}{l}{s^2} = \frac{1}{{80}}\left[ {2.{{\left( {0,5 - 5,7875} \right)}^2} + 3.{{\left( {1,5 - 5,7875} \right)}^2} + 3.{{\left( {2,5 - 5,7875} \right)}^2} + 5.{{\left( {3,5 - 5,7875} \right)}^2} + } \right.\\ + 8.{\left( {4,5 - 5,7875} \right)^2} + 20.{\left( {5,5 - 5,7875} \right)^2} + 16.{\left( {6,5 - 5,7875} \right)^2} + 15.{\left( {7,5 - 5,7875} \right)^2} + \\\left. { + 6.{{\left( {8,5 - 5,7875} \right)}^2} + 2.{{\left( {9,5 - 5,7875} \right)}^2}} \right] = \frac{{24671}}{{6400}} \approx 3,85\end{array}\) Vậy c) đúng. Độ lệch chuẩn của mẫu số liệu ghép nhóm là: \(s = \sqrt {3,85} \approx 1,962\). Vậy d) đúng. a) S. b) Đ. c) Đ. d) Đ.  Chia sẻ Bình luận
Quảng cáo
Group Ôn Thi ĐGNL & ĐGTD Miễn Phí
|
