Đề thi học kì 2 Toán 11 - Đề số 5Đề bài
Câu 1 :
Trong các khẳng định sau, khẳng định nào đúng ?
Câu 2 :
Hàm số \(y = {\left( {{x^2} + 1} \right)^3}\) có đạo hàm cấp ba là:
Câu 3 :
Cho hình chóp $S.ABCD$ có đáy $ABCD $ là hình vuông cạnh $a.$ Cạnh bên $SA$ vuông góc với mặt phẳng $(ABCD).$ Đường thẳng $SC$ tạo với mặt phẳng đáy góc ${45^0}.$ Khoảng cách giữa hai đường thẳng $SB$ và $AC$ là
Câu 4 :
Cho tứ diện $ABCD$ đều cạnh bằng $a$. Gọi $O$ là tâm đường tròn ngoại tiếp tam giác $BCD$. Góc giữa $AO$ và $CD$ bằng bao nhiêu?
Câu 5 :
Cho hàm số \(f\left( x \right) = \left\{ {\begin{array}{*{20}{l}}{{x^2} - 1}&{{\rm{khi}}\;\;x \ge 0}\\{ - {x^2}}&{{\rm{khi}}\;\;x < 0}\end{array}} \right..\) Khẳng định nào sau đây sai?
Câu 6 :
Cho hình lập phương\(ABCD.A'B'C'D'\). Gọi $\alpha $ là góc giữa $AC'$ và mp $\left( {A'BCD'} \right).$ Chọn khẳng định đúng trong các khẳng định sau?
Câu 7 :
Kết quả của giới hạn $\mathop {\lim }\limits_{x \to {{\left( { - 2} \right)}^ + }} \dfrac{{\left| {3x + 6} \right|}}{{x + 2}}$ là:
Câu 8 :
Tiếp tuyến tại điểm \(M\left( {1;3} \right)\) cắt đồ thị hàm số \(y = {x^3} - x + 3\) tại điểm thứ hai khác $M$ là $N$. Tọa độ điểm $N$ là:
Câu 9 :
Hàm số \(y = {\left( {{x^2} + 1} \right)^3}\) có đạo hàm cấp ba là:
Câu 10 :
Cho hình chóp \(S.ABC\) có cạnh \(SA \bot \left( {ABC} \right)\) và đáy \(ABC\) là tam giác cân ở \(C\). Gọi \(H\) và \(K\) lần lượt là trung điểm của \(AB\) và \(SB\). Khẳng định nào sau đây sai?
Câu 11 :
Cho ${u_n} = \dfrac{{{n^2} - 3n}}{{1 - 4{n^3}}}$. Khi đó $\lim {u_n}$bằng?
Câu 12 :
Cho hình chóp \(S.ABC\) có \(SA \bot \left( {ABC} \right),\) tam giác \(ABC\) vuông tại \(B\), kết luận nào sau đây sai?
Câu 13 :
Cho hàm số \(f\left( x \right) = - 4{x^3} + 4x - 1.\) Mệnh đề nào sau đây là sai?
Câu 14 :
Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình vuông tâm $O$, cạnh $a$. Đường thẳng $SO$ vuông góc với mặt phẳng đáy $\left( {ABCD} \right)$ và $SO = \dfrac{{a\sqrt 3 }}{2}$. Tính góc giữa hai mặt phẳng $\left( {SBC} \right)$ và $\left( {ABCD} \right)$.
Câu 15 :
Chọn mệnh đề đúng:
Câu 16 :
Cho hình chóp $S.ABC$ trong đó $SA,{\rm{ }}AB,{\rm{ }}BC$ đôi một vuông góc và $SA = AB = BC = 1.$ Khoảng cách giữa hai điểm $S$ và $C$ nhận giá trị nào trong các giá trị sau ?
Câu 17 :
Cho cấp số nhân lùi vô hạn \(\left( {{u_n}} \right)\) công bội $q$. Đặt \(S = {u_1} + {u_2} + ... + {u_n} + ...\) thì:
Câu 18 :
Biết rằng$\mathop {\lim }\limits_{x \to - \sqrt 3 } \dfrac{{2{x^3} + 6\sqrt 3 }}{{3 - {x^2}}} = a\sqrt 3 + b.$ Tính \({a^2} + {b^2}.\)
Câu 19 :
Cho hình lăng trụ $ABC.A'B'C'$ có đáy $ABC$ là tam giác vuông cân tại $A$ với $BC = a\sqrt 2 $; $AA' = a$ và vuông góc với đáy. Mặt phẳng $\left( \alpha \right)$ qua $M$ là trung điểm của $BC$ và vuông góc với $AB'$. Thiết diện tạo bởi $\left( \alpha \right)$ với hình lăng trụ $ABC.A'B'C'$ là:
Câu 20 :
Cho hàm số \(y = \dfrac{3}{{1 - x}}\). Để \(y' < 0\) thì $x$ nhận các giá trị thuộc tập nào sau đây?
Câu 21 :
Cho hàm số \(f\left( x \right) = \left\{ {\begin{array}{*{20}{l}}{\dfrac{{2x}}{{\sqrt {1 - x} }}}\,\,khi\,\,{x < 1}\\{\sqrt {3{x^2} + 1} }\,\,khi\,\,{x \ge 1}\end{array}} \right..\) Khi đó \(\mathop {\lim }\limits_{x \to {1^ + }} f\left( x \right)\) là:
Câu 22 :
Tính $\mathop {\lim }\limits_{x \to - \infty } \left( {\sqrt {{x^2} + 1} + x - 1} \right)$ bằng?
Câu 23 :
Cho hàm số \(f\left( x \right) = \left\{ \begin{array}{l}\dfrac{{{x^2} - 1}}{{x - 1}} & {\rm{khi}}\,\,x < 3,\,\,x \ne 1\\4 & {\rm{khi}}\,\,x = 1\\\sqrt {x + 1} & {\rm{khi}}\,\,x \ge 3\end{array} \right.\). Hàm số \(f\left( x \right)\) liên tục tại:
Câu 24 :
Cho hàm số$f\left( x \right) = \left\{ \begin{array}{l}\sqrt {\dfrac{{{x^2} + 1}}{{{x^3} - x + 6}}} \,\,\,\,\,\,\,x \ne 3;x > - 2\\b + \sqrt 3 \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,x = 3;b \in \mathbb{R}\end{array} \right.$. Tìm $b$ để $f\left( x \right)$liên tục tại $x = 3$.
Câu 25 :
Nếu $f''\left( x \right) = \dfrac{{2\sin x}}{{{{\cos }^3}x}}$, thì $f(x)$ bằng:
Câu 26 :
Tính đạo hàm của hàm số sau: \(f\left( x \right) = \left\{ \begin{array}{l}{x^2} - 3x + 1\,\,\,\,khi\,\,x > 1\\2x + 2\,\,\,\,\,\,\,\,\,\,\,\,\,khi\,\,x \le 1\end{array} \right.\) ta được:
Câu 27 :
Cho tứ diện \(ABCD\) có \(AB = CD = a,IJ = \dfrac{{a\sqrt 3 }}{2}\) (\(I\), \(J\) lần lượt là trung điểm của \(BC\) và \(AD\)). Số đo góc giữa hai đường thẳng \(AB\) và \(CD\) là
Câu 28 :
Cho hình chóp tam giác đều $S.ABC$ đỉnh $S,$ có độ dài cạnh đáy bằng $a$ và cạnh bên bằng \(\dfrac{{a\sqrt 3 }}{2}\). Gọi $M$ và $N$ lần lượt là trung điểm của các cạnh $SB$ và $SC.$ Tính theo $a$ diện tích tam giác $AMN,$ biết rằng mặt phẳng $\left( {AMN} \right)$ vuông góc với mặt phẳng $\left( {SBC} \right).$
Câu 29 :
Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình chữ nhật với $AC = 2a,{\rm{ }}BC = a$. Đỉnh $S$ cách đều các điểm $A,{\rm{ }}B,{\rm{ }}C$. Tính khoảng cách \(d\) từ trung điểm $M$ của $SC$ đến mặt phẳng $\left( {SBD} \right)$.
Câu 30 :
Cho hình chóp $S.ABC $ có đáy $ABC$ là tam giác vuông tại $B, AB = 3a, BC = 4a.$ Cạnh bên $SA$ vuông góc với đáy. Góc tạo bởi giữa $SC$ và đáy bằng ${60^0}$. Gọi $M$ là trung điểm của $AC,$ tính khoảng cách $d$ giữa hai đường thẳng $AB$ và $SM.$
Câu 31 :
Cho hình hộp chữ nhật \(ABCD.A'B'C'D'\) có đáy \(ABCD\) là hình vuông cạnh \(a\sqrt 2 \), \(AA' = 2a\). Tính khoảng cách giữa đường thẳng \(BD\) và mặt phẳng \(\left( {CB'D'} \right)\).
Câu 32 :
Xác định giá trị thực \(k\) để hàm số \(f\left( x \right) = \left\{ {\begin{array}{*{20}{l}}{\dfrac{{{x^{2016}} + x - 2}}{{\sqrt {2018x + 1} - \sqrt {x + 2018} }}}&{{\rm{khi}}}&{x \ne 1}\\k&{{\rm{khi}}}&{x = 1}\end{array}} \right.\) liên tục tại \(x = 1\).
Câu 33 :
Cho hình chóp \(S.ABC\) có đáy \(ABC\) là tam giác vuông cân tại \(B\), \(BC = a\), cạnh bên $SA$ vuông góc với đáy, \(SA = a\sqrt 3 \). Gọi \(M\) là trung điểm của \(AC\). Tính côtang góc giữa hai mặt phẳng \(\left( {SBM} \right)\) và \(\left( {SAB} \right)\).
Câu 34 :
Biết \(\mathop {\lim }\limits_{x \to + \infty } \left( {\sqrt {4{x^2} - 3x + 1} - \left( {ax + b} \right)} \right) = 0\). Tính \(a - 4b\) ta được
Câu 35 :
Cho hàm số \(y = f\left( x \right) = \left\{ {\begin{array}{*{20}{l}}{a{x^2} + bx + 1}&{khi}&{x \ge 0}\\{ax - b - 1}&{khi}&{x < 0}\end{array}} \right.\). Khi hàm số \(y = f\left( x \right)\) có đạo hàm tại \({x_0} = 0\), hãy tính \(T = a + 2b\).
Lời giải và đáp án
Câu 1 :
Trong các khẳng định sau, khẳng định nào đúng ?
Đáp án : D Lời giải chi tiết :
Một đường thẳng vuông góc với một trong hai đường thẳng song song thì vuông góc với đường thẳng kia nên nếu $a$ và $b$ song song, nếu $a$ vuông góc với $c$ thì $b$ cũng vuông góc với $c$
Câu 2 :
Hàm số \(y = {\left( {{x^2} + 1} \right)^3}\) có đạo hàm cấp ba là:
Đáp án : C Phương pháp giải :
Cách 1: Sử dụng đạo hàm của hàm số hợp tính lần lượt đạo hàm cấp một, cấp hai, cấp ba. Cách 2: Sử dụng hằng đẳng thức \({\left( {a + b} \right)^3} = {a^3} + 3{a^2}b + 3a{b^2} + {b^3}\) trước khi tính đạo hàm. Lời giải chi tiết :
Cách 1: \(\begin{array}{l}y' = 3{\left( {{x^2} + 1} \right)^2}\left( {{x^2} + 1} \right)' = 6x{\left( {{x^2} + 1} \right)^2}\\y'' = 6{\left( {{x^2} + 1} \right)^2} + 6x.2\left( {{x^2} + 1} \right).2x\\\,\,\,\,\,\, = 6{\left( {{x^2} + 1} \right)^2} + 24{x^2}\left( {{x^2} + 1} \right)\\y''' = 12\left( {{x^2} + 1} \right).2x + 24.2x.\left( {{x^2} + 1} \right) + 24{x^2}.2x\\\,\,\,\,\,\,\, = 24x\left( {{x^2} + 1} \right) + 48x\left( {{x^2} + 1} \right) + 48{x^3}\\\,\,\,\,\,\, = 24x\left( {{x^2} + 1 + 2\left( {{x^2} + 1} \right) + 2{x^2}} \right) = 24x\left( {5{x^2} + 3} \right)\end{array}\) Cách 2: \(\begin{array}{l}y = {\left( {{x^2} + 1} \right)^3} = {x^6} + 3{x^4} + 3{x^2} + 1\\y' = 6{x^5} + 12{x^3} + 6x\\y'' = 30{x^4} + 36{x^2} + 6\\y''' = 120{x^3} + 72x = 24x\left( {5{x^2} + 3} \right)\end{array}\)
Câu 3 :
Cho hình chóp $S.ABCD$ có đáy $ABCD $ là hình vuông cạnh $a.$ Cạnh bên $SA$ vuông góc với mặt phẳng $(ABCD).$ Đường thẳng $SC$ tạo với mặt phẳng đáy góc ${45^0}.$ Khoảng cách giữa hai đường thẳng $SB$ và $AC$ là
Đáp án : C Phương pháp giải :
Dựa vào phương pháp xác định mặt phẳng chứa đường thẳng này và song song với đường thẳng kia đưa về tính khoảng cách từ một điểm đến một mặt phẳng Lời giải chi tiết :
 Ta có $AC = a\sqrt 2 ;\widehat {SCA} = \widehat {\left( {SC;\left( {ABCD} \right)} \right)} = {45^0} \Rightarrow SA = AC = a\sqrt 2 $ Dựng $Bx||AC \Rightarrow d\left( {AC;SB} \right) = d\left( {AC;(SBx)} \right)$ Dựng $AE \bot Bx,\;AF \bot SE\,\,\,\left( 1 \right)$ ta có: \(\left\{ \begin{array}{l}Bx \bot AE\\Bx \bot SA\end{array} \right. \Rightarrow Bx \bot \left( {SAE} \right) \Rightarrow Bx \bot AF\,\,\left( 2 \right)\) Từ (1) và (2) \( \Rightarrow AF \bot \left( {SBE} \right)\) \( \Rightarrow d = d\left( {AC;\left( {SBx} \right)} \right) = d\left( {A,\left( {SBx} \right)} \right) = AF\) Ta có $BE||AC \Rightarrow BE \bot BD$ dễ ràng suy ra $OEBO$ là hình chữ nhật suy ra $AE = OB = \dfrac{{a\sqrt 2 }}{2}.$ Vậy khoảng cách $d\left( {SB;AC} \right) = \dfrac{{AE.SA}}{{\sqrt {A{E^2} + S{A^2}} }} = \dfrac{{\dfrac{{a\sqrt 2 }}{2}.a\sqrt 2 }}{{\sqrt {{{\left( {\dfrac{{a\sqrt 2 }}{2}} \right)}^2} + {{\left( {a\sqrt 2 } \right)}^2}} }} = \dfrac{{a\sqrt {10} }}{5}$.
Câu 4 :
Cho tứ diện $ABCD$ đều cạnh bằng $a$. Gọi $O$ là tâm đường tròn ngoại tiếp tam giác $BCD$. Góc giữa $AO$ và $CD$ bằng bao nhiêu?
Đáp án : C Phương pháp giải :
- Gọi \(M\) là trung điểm của \(CD\). - Tính tích vô hướng của hai véc tơ \(\overrightarrow {AO} ,\overrightarrow {CD} \) rồi kết luận. Lời giải chi tiết :
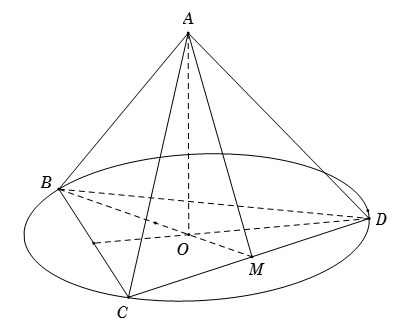 Gọi \(M\) là trung điểm của \(CD\). Vì $ABCD$ là tứ diện đều nên \(AM \bot CD,\,\,OM \bot CD.\) Ta có \(\overrightarrow {CD} .\overrightarrow {AO} = \overrightarrow {CD} .\left( {\overrightarrow {AM} + \overrightarrow {MO} } \right) = \overrightarrow {CD} .\overrightarrow {AM} + \overrightarrow {CD} .\overrightarrow {MO} = 0.\) Suy ra \(\overrightarrow {AO} \bot \overrightarrow {CD} \) nên số đo góc giữa hai đường thẳng $AO$ và $CD$ bằng \({90^0}.\)
Câu 5 :
Cho hàm số \(f\left( x \right) = \left\{ {\begin{array}{*{20}{l}}{{x^2} - 1}&{{\rm{khi}}\;\;x \ge 0}\\{ - {x^2}}&{{\rm{khi}}\;\;x < 0}\end{array}} \right..\) Khẳng định nào sau đây sai?
Đáp án : D Phương pháp giải :
Xét tính đúng sai của mỗi đáp án bằng cách xét tính liên tục và đạo hàm của hàm số tại các điểm \(x = 0,x = 2\). Lời giải chi tiết :
Dễ thấy \(f\left( x \right) = {x^2} - 1\) khi \(x \ge 0\) là hàm đa thức nên nó liên tục tại \(x = 2\). Ngoài ra \(\mathop {\lim }\limits_{x \to 2} \dfrac{{f\left( x \right) - f\left( 2 \right)}}{{x - 2}}\) \( = \mathop {\lim }\limits_{x \to 2} \dfrac{{\left( {{x^2} - 1} \right) - \left( {{2^2} - 1} \right)}}{{x - 2}}\) \( = \mathop {\lim }\limits_{x \to 2} \dfrac{{{x^2} - 4}}{{x - 2}} = \mathop {\lim }\limits_{x \to 2} \left( {x + 2} \right) = 4\) Do đó hàm số liên tục và có đạo hàm tại \(x = 2\). Xét các giới hạn $\left\{ \begin{array}{l}\mathop {\lim }\limits_{x \to {0^ + }} f\left( x \right) = \mathop {\lim }\limits_{x \to {0^ + }} \left( {{x^2} - 1} \right) = - 1\\\mathop {\lim }\limits_{x \to {0^ - }} f\left( x \right) = \mathop {\lim }\limits_{x \to {0^ - }} \left( { - {x^2}} \right) = 0\end{array} \right..$ Do $\mathop {\lim }\limits_{x \to {0^ + }} f\left( x \right) \ne \mathop {\lim }\limits_{x \to {0^ - }} f\left( x \right)$ nên hàm số không liên tục tại \(x = 0\). Do đó, hàm số không có đạo hàm tại \(x = 0\).
Câu 6 :
Cho hình lập phương\(ABCD.A'B'C'D'\). Gọi $\alpha $ là góc giữa $AC'$ và mp $\left( {A'BCD'} \right).$ Chọn khẳng định đúng trong các khẳng định sau?
Đáp án : D Phương pháp giải :
- Tìm giao điểm \(I\) của \(AC'\) với \(\left( {A'BCD'} \right)\). - Tìm hình chiếu \(H\) của \(C'\) trên \(\left( {A'BCD'} \right)\) bằng cách tìm một đường thẳng qua \(C'\) mà vuông góc với \(\left( {A'BCD'} \right)\). - Góc cần tìm là góc giữa \(C'I\) và hình chiếu \(HI\) của nó trên mặt phẳng \(\left( {A'BCD'} \right)\). Lời giải chi tiết :
Gọi $\left\{ \begin{array}{l}A'C \cap AC' = I\\C'D \cap CD' = H\end{array} \right.$ mà \(\left\{ \begin{array}{l}C'D \bot CD'\\C'D \bot A'D'\end{array} \right. \Rightarrow C'D \bot \left( {A'BCD'} \right) \Rightarrow IH\) là hình chiếu vuông góc của \(IC'\) lên \(\left( {A'BCD'} \right) \Rightarrow \widehat {C'IH}\)là góc giữa \(IC'\) và \(\left( {A'BCD'} \right)\) và cũng là góc giữa \(AC'\) và \(\left( {A'BCD'} \right).\) Mà \(\tan \widehat {C'IH} = \dfrac{{C'H}}{{IH}} = \dfrac{1}{{\sqrt 2 }}.2 = \sqrt 2 .\)
Câu 7 :
Kết quả của giới hạn $\mathop {\lim }\limits_{x \to {{\left( { - 2} \right)}^ + }} \dfrac{{\left| {3x + 6} \right|}}{{x + 2}}$ là:
Đáp án : B Phương pháp giải :
Phá dấu giá trị tuyệt đối dựa vào điều kiện của \(x\). Lời giải chi tiết :
Ta có \(\left| {x + 2} \right| = x + 2\) với mọi \(x > - 2,\) do đó : $\mathop {\lim }\limits_{x \to {{\left( { - 2} \right)}^ + }} \dfrac{{\left| {3x + 6} \right|}}{{x + 2}} = \mathop {\lim }\limits_{x \to {{\left( { - 2} \right)}^ + }} \dfrac{{3\left| {x + 2} \right|}}{{x + 2}} = \mathop {\lim }\limits_{x \to {{\left( { - 2} \right)}^ + }} \dfrac{{3\left( {x + 2} \right)}}{{x + 2}} = 3$
Câu 8 :
Tiếp tuyến tại điểm \(M\left( {1;3} \right)\) cắt đồ thị hàm số \(y = {x^3} - x + 3\) tại điểm thứ hai khác $M$ là $N$. Tọa độ điểm $N$ là:
Đáp án : A Phương pháp giải :
Phương trình tiếp tuyến của \(\left( C \right)\) tại điểm \(M\left( {{x_o};{y_0}} \right)\) là: \(y = f'\left( {{x_0}} \right)\left( {x - {x_0}} \right) + {y_0}\) Tìm giao điểm của tiếp tuyến vừa tìm được với đồ thị hàm số ban đầu. Lời giải chi tiết :
\(y' = 3{x^2} - 1 \Rightarrow y'\left( 1 \right) = 2\) \( \Rightarrow \) phương trình tiếp tuyến của đồ thị hàm số tại điểm \(M\left( {1;3} \right)\) là: \(y = 2\left( {x - 1} \right) + 3 = 2x + 1\) Xét phương trình hoành độ giao điểm \({x^3} - x + 3 = 2x + 1 \Leftrightarrow {x^3} - 3x + 2 = 0 \Leftrightarrow \left[ \begin{array}{l}x = - 2 \Rightarrow y = - 3 \Rightarrow N\left( { - 2; - 3} \right)\\x = 1\end{array} \right.\)
Câu 9 :
Hàm số \(y = {\left( {{x^2} + 1} \right)^3}\) có đạo hàm cấp ba là:
Đáp án : C Phương pháp giải :
Cách 1: Sử dụng đạo hàm của hàm số hợp tính lần lượt đạo hàm cấp một, cấp hai, cấp ba. Cách 2: Sử dụng hằng đẳng thức \({\left( {a + b} \right)^3} = {a^3} + 3{a^2}b + 3a{b^2} + {b^3}\) trước khi tính đạo hàm. Lời giải chi tiết :
Cách 1: \(\begin{array}{l}y' = 3{\left( {{x^2} + 1} \right)^2}\left( {{x^2} + 1} \right)' = 6x{\left( {{x^2} + 1} \right)^2}\\y'' = 6{\left( {{x^2} + 1} \right)^2} + 6x.2\left( {{x^2} + 1} \right).2x\\\,\,\,\,\,\, = 6{\left( {{x^2} + 1} \right)^2} + 24{x^2}\left( {{x^2} + 1} \right)\\y''' = 12\left( {{x^2} + 1} \right).2x + 24.2x.\left( {{x^2} + 1} \right) + 24{x^2}.2x\\\,\,\,\,\,\,\, = 24x\left( {{x^2} + 1} \right) + 48x\left( {{x^2} + 1} \right) + 48{x^3}\\\,\,\,\,\,\, = 24x\left( {{x^2} + 1 + 2\left( {{x^2} + 1} \right) + 2{x^2}} \right) = 24x\left( {5{x^2} + 3} \right)\end{array}\) Cách 2: \(\begin{array}{l}y = {\left( {{x^2} + 1} \right)^3} = {x^6} + 3{x^4} + 3{x^2} + 1\\y' = 6{x^5} + 12{x^3} + 6x\\y'' = 30{x^4} + 36{x^2} + 6\\y''' = 120{x^3} + 72x = 24x\left( {5{x^2} + 3} \right)\end{array}\)
Câu 10 :
Cho hình chóp \(S.ABC\) có cạnh \(SA \bot \left( {ABC} \right)\) và đáy \(ABC\) là tam giác cân ở \(C\). Gọi \(H\) và \(K\) lần lượt là trung điểm của \(AB\) và \(SB\). Khẳng định nào sau đây sai?
Đáp án : D Phương pháp giải :
Sử dụng điều kiện đường thẳng vuông góc với mặt phẳng để xét tính đúng sai của từng đáp án. Lời giải chi tiết :
 Do \(\Delta ABC\) cân tại \(C\) nên \(CH \bot AB\). Mà \(SA \bot \left( {ABC} \right) \Rightarrow SA \bot CH\). Do đó \(CH \bot \left( {SAB} \right) \Rightarrow CH \bot HK,CH \bot AK\) hay A, C đúng. Ngoài ra \(HK//SA,SA \bot AB \Rightarrow HK \bot AB\), mà \(AB \bot CH\) \( \Rightarrow AB \bot \left( {CHK} \right)\) hay B đúng. D sai vì \(BC\) không vuông góc với \(AC\) nên không có \(BC \bot \left( {SAC} \right)\).
Câu 11 :
Cho ${u_n} = \dfrac{{{n^2} - 3n}}{{1 - 4{n^3}}}$. Khi đó $\lim {u_n}$bằng?
Đáp án : A Phương pháp giải :
Chia cả tử mẫu của phân thức cho ${n^3}$. Lời giải chi tiết :
$\lim {u_n} = \lim \dfrac{{{n^2} - 3n}}{{1 - 4{n^3}}} = \lim \dfrac{{\dfrac{1}{n} - \dfrac{3}{{{n^2}}}}}{{\dfrac{1}{{{n^3}}} - 4}} = \dfrac{0}{{ - 4}} = 0.$
Câu 12 :
Cho hình chóp \(S.ABC\) có \(SA \bot \left( {ABC} \right),\) tam giác \(ABC\) vuông tại \(B\), kết luận nào sau đây sai?
Đáp án : A Phương pháp giải :
Xét tính đúng sai của từng đáp án, sử dụng lý thuyết: Nếu một đường thẳng vuông góc với một mặt phẳng thì mọi mặt phẳng chứa đường thẳng đều vuông góc với mặt phẳng đã cho. Xét đáp án A: Nếu hai mặt phẳng vuông góc với nhau thì mọi đường thẳng nằm trong mặt phẳng này vuông góc với giao tuyến đều vuông góc với mặt phẳng kia. Lời giải chi tiết :
+) Nếu đáp án A đúng: \(\left( {SAC} \right) \bot \left( {SAB} \right)\) Vì \(SA \bot \left( {ABC} \right) \Rightarrow SA \bot AB\) Mà SA là giao tuyến của hai mặt phẳng vuông góc \(\left( {SAC} \right) \bot \left( {SAB} \right)\) \( \Rightarrow AB \bot \left( {SAC} \right) \Rightarrow AB \bot AC\) (Vô lý vì tam giác ABC vuông tại B.) Vậy A sai. +) Ta có: \(\left\{ \begin{array}{l}SA \bot \left( {ABC} \right)\\SA \subset \left( {SAB} \right),\left( {SAC} \right)\end{array} \right.\) \( \Rightarrow \) \(\left( {SAB} \right),\,\left( {SAC} \right) \bot \left( {ABC} \right)\) \( \Rightarrow \) B, C đúng. \(SA \bot \left( {ABC} \right) \Rightarrow SA \bot BC\) mà \(BC \bot AB\) \( \Rightarrow \) \(BC \bot \left( {SAB} \right);BC \subset \left( {SBC} \right)\) \( \Rightarrow \) \(\left( {SAB} \right) \bot \left( {SBC} \right)\) \( \Rightarrow \) D đúng.
Câu 13 :
Cho hàm số \(f\left( x \right) = - 4{x^3} + 4x - 1.\) Mệnh đề nào sau đây là sai?
Đáp án : B Phương pháp giải :
Xét tính đúng sai của từng đáp án và kết luận. Lời giải chi tiết :
(i) Hàm \(f\left( x \right)\) là hàm đa thức nên liên tục trên \(\mathbb{R}\) nên A đúng. (ii) Ta có \(\left\{ \begin{array}{l}f\left( { - 1} \right) = - 1 < 0\\f\left( { - 2} \right) = 23 > 0\end{array} \right. \Rightarrow f\left( x \right) = 0\) có nghiệm \({x_1}\) trên \(\left( { - 2;1} \right)\), mà $\left( { - 2; - 1} \right) \subset \left( { - 2;0} \right) \subset \left( { - \infty ;1} \right)$ nên B sai và C đúng. (iii) Ta có \(\left\{ \begin{array}{l}f\left( 0 \right) = - 1 < 0\\f\left( {\dfrac{1}{2}} \right) = \dfrac{1}{2} > 0\end{array} \right. \Rightarrow f\left( x \right) = 0\) có nghiệm \({x_2}\) thuộc \(\left( {0;\dfrac{1}{2}} \right).\) Kết hợp với (1) suy ra \(f\left( x \right) = 0\) có các nghiệm \({x_1},\,\,{x_2}\) thỏa: \( - 3 < {x_1} < - 1 < 0 < {x_2} < \dfrac{1}{2}\) nên D đúng.
Câu 14 :
Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình vuông tâm $O$, cạnh $a$. Đường thẳng $SO$ vuông góc với mặt phẳng đáy $\left( {ABCD} \right)$ và $SO = \dfrac{{a\sqrt 3 }}{2}$. Tính góc giữa hai mặt phẳng $\left( {SBC} \right)$ và $\left( {ABCD} \right)$.
Đáp án : C Phương pháp giải :
Sử dụng phương pháp xác định góc giữa hai mặt phẳng và áp dụng các hệ thức lượng trong tam giác vuông Lời giải chi tiết :
Gọi \(Q\) là trung điểm \(BC\), suy ra \(OQ \bot BC\). Ta có $\left\{ \begin{array}{l}BC \bot OQ\\BC \bot SO\end{array} \right. \Rightarrow BC \bot \left( {SOQ} \right) \Rightarrow BC \bot SQ.$ Do đó $\left\{ \begin{array}{l}\left( {SBC} \right) \cap \left( {ABCD} \right) = BC\\\left( {SBC} \right) \supset SQ \bot BC\\\left( {ABCD} \right) \supset OQ \bot BC\end{array} \right. \Rightarrow \widehat {\left( {\left( {SBC} \right);\left( {ABCD} \right)} \right)} = \widehat {\left( {SQ;OQ} \right)} = \widehat {SQO}.$ Tam giác vuông $SOQ$, có $\tan \widehat {SQO} = \dfrac{{SO}}{{OQ}} = \sqrt 3 \Rightarrow \widehat {SQO} = {60^0}$ Vậy mặt phẳng $\left( {SBC} \right)$ hợp với mặt đáy $\left( {ABCD} \right)$ một góc ${60^0}.$ 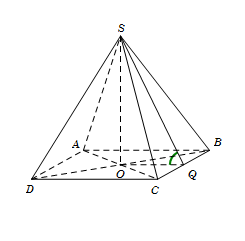
Câu 15 :
Chọn mệnh đề đúng:
Đáp án : B Lời giải chi tiết :
Ta có: \(\mathop {\lim }\limits_{x \to + \infty } f\left( x \right) = + \infty \Leftrightarrow \mathop {\lim }\limits_{x \to + \infty } \left[ { - f\left( x \right)} \right] = - \infty \)
Câu 16 :
Cho hình chóp $S.ABC$ trong đó $SA,{\rm{ }}AB,{\rm{ }}BC$ đôi một vuông góc và $SA = AB = BC = 1.$ Khoảng cách giữa hai điểm $S$ và $C$ nhận giá trị nào trong các giá trị sau ?
Đáp án : B Phương pháp giải :
- Chứng minh \(SA \bot \left( {ABC} \right)\) rồi suy ra \(SA \bot AC\) - Sử dụng định lý Pi-ta-go cho tam giác vuông \(SAC\) Lời giải chi tiết :
Do $\left\{ \begin{array}{l}SA \bot AB\\SA \bot BC\end{array} \right.$ nên $SA \bot (ABC) \Rightarrow SA \bot AC$ Như vậy \(SC = \sqrt {S{A^2} + A{C^2}} = \sqrt {S{A^2} + A{B^2} + B{C^2}} = \sqrt 3 \) 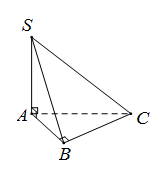
Câu 17 :
Cho cấp số nhân lùi vô hạn \(\left( {{u_n}} \right)\) công bội $q$. Đặt \(S = {u_1} + {u_2} + ... + {u_n} + ...\) thì:
Đáp án : A Lời giải chi tiết :
Công thức tính tổng cấp số nhân lùi vô hạn: \(S = {u_1} + {u_2} + ... + {u_n} + ... = \dfrac{{{u_1}}}{{1 - q}}\).
Câu 18 :
Biết rằng$\mathop {\lim }\limits_{x \to - \sqrt 3 } \dfrac{{2{x^3} + 6\sqrt 3 }}{{3 - {x^2}}} = a\sqrt 3 + b.$ Tính \({a^2} + {b^2}.\)
Đáp án : A Phương pháp giải :
Đưa tử và mẫu của phân thức về dạng tích, khử dạng vô định và tính giới hạn. Lời giải chi tiết :
Ta có $\mathop {\lim }\limits_{x \to - \sqrt 3 } \dfrac{{2({x^3} + 3\sqrt 3 )}}{{3 - {x^2}}}$ $ = \mathop {\lim }\limits_{x \to - \sqrt 3 } \dfrac{{2\left( {x + \sqrt 3 } \right)\left( {{x^2} - \sqrt 3 x + 3} \right)}}{{\left( {\sqrt 3 - x} \right)\left( {\sqrt 3 + x} \right)}}$ $ = \mathop {\lim }\limits_{x \to - \sqrt 3 } \dfrac{{2\left( {{x^2} - \sqrt 3 x + 3} \right)}}{{\sqrt 3 - x}}$ $ = \dfrac{{2\left[ {{{\left( { - \sqrt 3 } \right)}^2} - \sqrt 3 .\left( { - \sqrt 3 } \right) + 3} \right]}}{{\sqrt 3 - \left( { - \sqrt 3 } \right)}} = \dfrac{{18}}{{2\sqrt 3 }} = 3\sqrt 3 $ $ \Rightarrow \left\{ \begin{array}{l}a = 3\\b = 0\end{array} \right. \Rightarrow {a^2} + {b^2} = 9$.
Câu 19 :
Cho hình lăng trụ $ABC.A'B'C'$ có đáy $ABC$ là tam giác vuông cân tại $A$ với $BC = a\sqrt 2 $; $AA' = a$ và vuông góc với đáy. Mặt phẳng $\left( \alpha \right)$ qua $M$ là trung điểm của $BC$ và vuông góc với $AB'$. Thiết diện tạo bởi $\left( \alpha \right)$ với hình lăng trụ $ABC.A'B'C'$ là:
Đáp án : B Phương pháp giải :
- Tìm một đường thẳng qua \(M\) và vuông góc với \(\left( {ABB'A'} \right)\) thì đường thẳng đó sẽ vuông góc với \(AB'\). - Sử dụng các tính chất đường thẳng song song mặt phẳng, định lý ba đường giao tuyến để dựng thiết diện cần tìm. - Sử dụng các quan hệ vuông góc, song song để chứng minh thiết diện là hình thang vuông. Lời giải chi tiết :
Gọi N là trung điểm $AB \Rightarrow MN//AC \Rightarrow MN \bot AB$. Ta có $\left\{ \begin{array}{l}MN \bot AB\\MN \bot AA'\end{array} \right. \Rightarrow MN \bot \left( {ABB'A'} \right) \Rightarrow MN \bot AB' \Rightarrow MN \subset \left( \alpha \right).$ Từ giả thiết $ \Rightarrow $$AB = a = AA' \Rightarrow ABB'A'$ là hình vuông $ \Rightarrow BA' \bot AB'$ Trong mp $\left( {ABB'A'} \right)$ kẻ $NQ\parallel BA'$ với $Q \in AA'$. Trong mp $\left( {ACC'A'} \right)$ kẻ $QR\parallel AC$ với $R \in CC'$. Vậy thiết diện là hình thang MNPQ vuông (do MN và QR cùng song song với AC và $MN \bot NQ$). 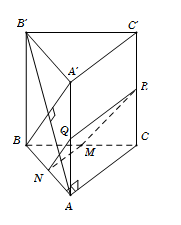
Câu 20 :
Cho hàm số \(y = \dfrac{3}{{1 - x}}\). Để \(y' < 0\) thì $x$ nhận các giá trị thuộc tập nào sau đây?
Đáp án : C Phương pháp giải :
Bước 1: Tìm đạo hàm bằng cách sử dụng công thức tính đạo hàm của một thương \(\left( {\dfrac{u}{v}} \right)' = \dfrac{{u'v - uv'}}{{{v^2}}}\) Bước 2: Đánh giá y' để tìm tập nghiệm. Lời giải chi tiết :
Bước 1: \(y' = \dfrac{{3'\left( {1 - x} \right) - 3\left( {1 - x} \right)'}}{{{{\left( {1 - x} \right)}^2}}} = \dfrac{{ - 3.\left( { - 1} \right)}}{{{{\left( {1 - x} \right)}^2}}} \)\(= \dfrac{3}{{{{\left( {1 - x} \right)}^2}}} \) Bước 2: Ta có \(y'=\dfrac{3}{{{{\left( {1 - x} \right)}^2}}} > 0\,\,\forall x \ne 1 \) \(\Rightarrow \)Tập nghiệm của bất phương trình \(y' < 0\) là \(\emptyset \).
Câu 21 :
Cho hàm số \(f\left( x \right) = \left\{ {\begin{array}{*{20}{l}}{\dfrac{{2x}}{{\sqrt {1 - x} }}}\,\,khi\,\,{x < 1}\\{\sqrt {3{x^2} + 1} }\,\,khi\,\,{x \ge 1}\end{array}} \right..\) Khi đó \(\mathop {\lim }\limits_{x \to {1^ + }} f\left( x \right)\) là:
Đáp án : B Phương pháp giải :
Tìm hàm số trong khoảng thích hợp và tính giới hạn. Lời giải chi tiết :
\(\mathop {\lim }\limits_{x \to {1^ + }} f\left( x \right) = \mathop {\lim }\limits_{x \to {1^ + }} \sqrt {3{x^2} + 1} = \sqrt {{{3.1}^2} + 1} = 2\)
Câu 22 :
Tính $\mathop {\lim }\limits_{x \to - \infty } \left( {\sqrt {{x^2} + 1} + x - 1} \right)$ bằng?
Đáp án : A Phương pháp giải :
- Nhân liên hợp để khử dạng $\infty - \infty $ - Chia cả tử và mẫu cho lũy thừa của $x$ bậc cao nhất. - Thay giới hạn $\mathop {\lim }\limits_{x \to \infty } \dfrac{C}{{{x^n}}} = 0,\,\,\,n \in {\mathbb{N}^*}$. Lời giải chi tiết :
$\begin{array}{l}\mathop {\lim }\limits_{x \to - \infty } \left( {\sqrt {{x^2} + 1} + x - 1} \right) \\ = \mathop {\lim }\limits_{x \to - \infty } \dfrac{{\left( {\sqrt {{x^2} + 1} + x - 1} \right)\left( {\sqrt {{x^2} + 1} - x + 1} \right)}}{{\sqrt {{x^2} + 1} - x + 1}} \\= \mathop {\lim }\limits_{x \to - \infty } \dfrac{{{x^2} + 1 - {{(x - 1)}^2}}}{{\sqrt {{x^2} + 1} - x + 1}}\\=\mathop {\lim }\limits_{x \to - \infty } \dfrac{{{x^2} + 1 - {x^2} + 2x - 1}}{{\sqrt {{x^2} + 1} - x + 1}} \\= \mathop {\lim }\limits_{x \to - \infty } \dfrac{{2x}}{{\sqrt {{x^2} + 1} - x + 1}} \\= \mathop {\lim }\limits_{x \to - \infty } \dfrac{{\dfrac{{2x}}{x}}}{{\dfrac{{\sqrt {{x^2} + 1} }}{x} - \dfrac{x}{x} + \dfrac{1}{x}}} \\= \mathop {\lim }\limits_{x \to - \infty } \dfrac{2}{{ - \sqrt {1 + \dfrac{1}{{{x^2}}}} - 1 + \dfrac{1}{x}}}\\ = \dfrac{2}{{ - 1 - 1 + 0}} = - 1\end{array}$
Câu 23 :
Cho hàm số \(f\left( x \right) = \left\{ \begin{array}{l}\dfrac{{{x^2} - 1}}{{x - 1}} & {\rm{khi}}\,\,x < 3,\,\,x \ne 1\\4 & {\rm{khi}}\,\,x = 1\\\sqrt {x + 1} & {\rm{khi}}\,\,x \ge 3\end{array} \right.\). Hàm số \(f\left( x \right)\) liên tục tại:
Đáp án : D Phương pháp giải :
Hàm số liên tục trên một khoảng nếu nó liên tục tại mọi điểm thuộc khoảng đó. Lời giải chi tiết :
Hàm số \(y = f\left( x \right)\) có TXĐ: \({\rm{D}} = \mathbb{R}\). Dễ thấy hàm số \(y = f\left( x \right)\) liên tục trên mỗi khoảng \(\left( { - \infty ;1} \right),\left( {1;3} \right)\) và \(\left( {3; + \infty } \right)\). Ta có \(\left\{ \begin{array}{l}f\left( 1 \right) = 4\\\mathop {\lim }\limits_{x \to 1} f\left( x \right) = \mathop {\lim }\limits_{x \to 1} \dfrac{{{x^2} - 1}}{{x - 1}} = \mathop {\lim }\limits_{x \to 1} \left( {x + 1} \right) = 2\end{array} \right.\) \( \Rightarrow f\left( x \right)\) gián đoạn tại \(x = 1.\) Ta có \(\left\{ \begin{array}{l}f\left( 3 \right) = 2\\\mathop {\lim }\limits_{x \to {3^ - }} f\left( x \right) = \mathop {\lim }\limits_{x \to {3^ - }} \dfrac{{{x^2} - 1}}{{x - 1}} = \mathop {\lim }\limits_{x \to {3^ - }} \left( {x + 1} \right) = 4\end{array} \right.\) \( \Rightarrow f\left( x \right)\) gián đoạn tại \(x = 3.\)
Câu 24 :
Cho hàm số$f\left( x \right) = \left\{ \begin{array}{l}\sqrt {\dfrac{{{x^2} + 1}}{{{x^3} - x + 6}}} \,\,\,\,\,\,\,x \ne 3;x > - 2\\b + \sqrt 3 \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,x = 3;b \in \mathbb{R}\end{array} \right.$. Tìm $b$ để $f\left( x \right)$liên tục tại $x = 3$.
Đáp án : D Phương pháp giải :
- Tính giới hạn $\mathop {\lim }\limits_{x \to 3} f\left( x \right),f\left( 3 \right)$. - Điều kiện để hàm số liên tục tại \(x = 3\) nếu $\mathop {\lim }\limits_{x \to 3} f\left( x \right) = f\left( 3 \right)$. Lời giải chi tiết :
Hàm số liên tục tại $x = 3 \Leftrightarrow \mathop {\lim }\limits_{x \to 3} f\left( x \right) = f\left( 3 \right)$. Ta có: $\mathop {\lim }\limits_{x \to 3} \sqrt {\dfrac{{{x^2} + 1}}{{{x^3} - x + 6}}} = \sqrt {\dfrac{1}{3}} $, $f\left( 3 \right) = b + \sqrt 3 $. Vậy: $b + \sqrt 3 = \sqrt {\dfrac{1}{3}} \Leftrightarrow b = - \sqrt 3 + \dfrac{1}{{\sqrt 3 }} = \dfrac{{ - 2}}{{\sqrt 3 }}$.
Câu 25 :
Nếu $f''\left( x \right) = \dfrac{{2\sin x}}{{{{\cos }^3}x}}$, thì $f(x)$ bằng:
Đáp án : D Phương pháp giải :
Thử từng đáp án Lời giải chi tiết :
Đáp án A: \(\begin{array}{l}y = \dfrac{1}{{\cos x}}\\y' = \dfrac{{ - \left( {\cos x} \right)'}}{{{{\cos }^2}x}} = \dfrac{{\sin x}}{{{{\cos }^2}x}}\\y'' = \dfrac{{\cos x.{{\cos }^2}x - \sin x.2\cos x\left( {\cos x} \right)'}}{{{{\left( {{{\cos }^2}x} \right)}^2}}} = \dfrac{{{{\cos }^3}x + 2{{\sin }^2}x\cos x}}{{{{\cos }^4}x}} = \dfrac{{{{\cos }^2}x + 2{{\sin }^2}x}}{{{{\cos }^3}x}}\end{array}\). Đáp án B: \(\begin{array}{l}y = - \dfrac{1}{{\cos x}}\\y' = \dfrac{{\left( {\cos x} \right)'}}{{{{\cos }^2}x}} = - \dfrac{{\sin x}}{{{{\cos }^2}x}}\\y'' = - \dfrac{{\cos x.{{\cos }^2}x - \sin x.2\cos x\left( {\cos x} \right)'}}{{{{\cos }^4}x}} = \dfrac{{ - {{\cos }^3}x - 2{{\sin }^2}x\cos x}}{{{{\cos }^4}x}} = - \dfrac{{{{\cos }^2}x + 2{{\sin }^2}x}}{{{{\cos }^4}x}}\end{array}\) Đáp án C: \(\begin{array}{l}y = \cot x\\y' = - \dfrac{1}{{{{\sin }^2}x}}\\y' = \dfrac{{2\sin x\left( {\sin x} \right)'}}{{{{\sin }^4}x}} = \dfrac{{2\sin x\cos x}}{{{{\sin }^4}x}} = \dfrac{{2\cos x}}{{{{\sin }^3}x}}\end{array}\) Đáp án D: \(\begin{array}{l}y = \tan x\\y' = \dfrac{1}{{{{\cos }^2}x}}\\y'' = \dfrac{{ - 2\cos x\left( {\cos x} \right)'}}{{{{\cos }^4}x}} = \dfrac{{2\sin x\cos x}}{{{{\cos }^4}x}} = \dfrac{{2\sin x}}{{{{\cos }^3}x}}\end{array}\)
Câu 26 :
Tính đạo hàm của hàm số sau: \(f\left( x \right) = \left\{ \begin{array}{l}{x^2} - 3x + 1\,\,\,\,khi\,\,x > 1\\2x + 2\,\,\,\,\,\,\,\,\,\,\,\,\,khi\,\,x \le 1\end{array} \right.\) ta được:
Đáp án : B Phương pháp giải :
+) Tính đạo hàm của hàm số khi \(x > 1\) +) Tính đạo hàm của hàm số khi \(x < 1\) +) Sử dụng định nghĩa đạo hàm, xét sự tồn tại của đạo hàm của hàm số tại x = 1. Lời giải chi tiết :
Với \(x > 1\) ta có: \(f\left( x \right) = {x^2} - 3x + 1 \Rightarrow f'\left( x \right) = 2x - 3\) Với \(x < 1\) ta có : \(f\left( x \right) = 2x + 2 \Leftrightarrow f'\left( x \right) = 2\) Với $x = 1$ ta có : \(\mathop {\lim }\limits_{x \to {1^ + }} f\left( x \right) = \mathop {\lim }\limits_{x \to {1^ + }} \left( {{x^2} - 3x + 1} \right) = - 1 \ne f\left( 1 \right) = 4 \) \(\Rightarrow \) Hàm số không liên tục tại $x = 1,$ do đó không có đạo hàm tại $x = 1.$ Vậy \(f'\left( x \right) = \left\{ \begin{array}{l}2x - 3\,\,\,khi\,\,x > 1\\2\,\,\,\,\,\,\,\,\,\,\,\,\,khi\,\,x < 1\end{array} \right.\)
Câu 27 :
Cho tứ diện \(ABCD\) có \(AB = CD = a,IJ = \dfrac{{a\sqrt 3 }}{2}\) (\(I\), \(J\) lần lượt là trung điểm của \(BC\) và \(AD\)). Số đo góc giữa hai đường thẳng \(AB\) và \(CD\) là
Đáp án : C Phương pháp giải :
Sử dụng tính chất: \(\left\{ \begin{array}{l}a//a'\\b//b'\end{array} \right. \Rightarrow \widehat {\left( {a,b} \right)} = \widehat {\left( {a',b'} \right)}\) Lời giải chi tiết :
Gọi \(M\), \(N\) lần lượt là trung điểm \(AC\), \(BD.\) Ta có: \(\left\{ \begin{array}{l}MI = NI = \dfrac{1}{2}AB = \dfrac{1}{2}CD = \dfrac{a}{2}\\MI{\text{ // }}AB{\text{ // }}NJ,MJ//CD//IN\end{array} \right. \Rightarrow MINJ\) là hình thoi. Gọi \(O\) là giao điểm của \(MN\) và \(IJ\). Ta có: \(\widehat {MIN} = 2\widehat {MIO}\). Xét \(\Delta MIO\) vuông tại \(O\), ta có: \(\cos \widehat {MIO} = \dfrac{{IO}}{{MI}} = \dfrac{{\dfrac{{a\sqrt 3 }}{4}}}{{\dfrac{a}{2}}} = \dfrac{{\sqrt 3 }}{2} \Rightarrow \widehat {MIO} = 30^\circ \Rightarrow \widehat {MIN} = 60^\circ \) Mà: \(\left( {AB,CD} \right) = \left( {IM,IN} \right) = \widehat {MIN} = 60^\circ \)
Câu 28 :
Cho hình chóp tam giác đều $S.ABC$ đỉnh $S,$ có độ dài cạnh đáy bằng $a$ và cạnh bên bằng \(\dfrac{{a\sqrt 3 }}{2}\). Gọi $M$ và $N$ lần lượt là trung điểm của các cạnh $SB$ và $SC.$ Tính theo $a$ diện tích tam giác $AMN,$ biết rằng mặt phẳng $\left( {AMN} \right)$ vuông góc với mặt phẳng $\left( {SBC} \right).$
Đáp án : D Lời giải chi tiết :
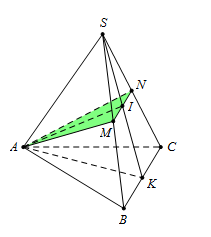 Gọi $K$ là trung điểm của $BC$ và $I = SK \cap MN$ Từ giả thiết $ \Rightarrow \,\,MN = \dfrac{1}{2}BC = \dfrac{a}{2},$ $MN\parallel BC$$ \Rightarrow \,\,I$ là trung điểm của $SK$ và $BC.$ Ta có $\Delta \,SAB = \Delta \,SAC$$ \Rightarrow $ Hai trung tuyến tương ứng $AM = AN.$ $ \Rightarrow \,\,\Delta \,AMN$ cân tại $A$$ \Rightarrow \,\,AI \bot MN.$ Mà $\left( {SBC} \right) \bot \left( {AMN} \right) \Rightarrow AI \bot \left( {SBC} \right)$ $ \Rightarrow \,\,AI \bot SK.$ Suy ra tam giác $SAK$ cân tại $A\,\, \Rightarrow \,\,SA = AK = \dfrac{{a\sqrt 3 }}{2}.$ Khi đó $S{K^2} = S{B^2} - B{K^2} = \dfrac{{{a^2}}}{2} \Rightarrow AI = \sqrt {S{A^2} - {{\left( {\dfrac{{SK}}{2}} \right)}^2}} = \dfrac{{a\sqrt {10} }}{4}.$ Vậy diện tích tam giác $AMN$ là ${S_{\Delta \,AMN}} = \dfrac{1}{2}MN.AI = \dfrac{{{a^2}\sqrt {10} }}{{16}}.$
Câu 29 :
Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình chữ nhật với $AC = 2a,{\rm{ }}BC = a$. Đỉnh $S$ cách đều các điểm $A,{\rm{ }}B,{\rm{ }}C$. Tính khoảng cách \(d\) từ trung điểm $M$ của $SC$ đến mặt phẳng $\left( {SBD} \right)$.
Đáp án : A Phương pháp giải :
Sử dụng phương pháp kẻ chân đường cao từ điểm đến mặt phẳng (lý thuyết đường thẳng vuông góc với mặt phẳng) để xác định khoảng cách từ một điểm đến mặt phẳng Lời giải chi tiết :
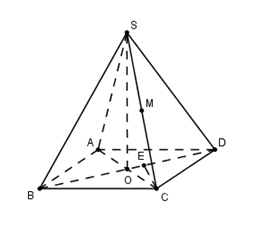 Gọi \(O\) là trung điểm \(AC\), suy ra \(O\) là tâm đường tròn ngoại tiếp tam giác \(ABC\). (Do tam giác $ABC$ vuông tại $B$). Do đỉnh $S$ cách đều các điểm $A,{\rm{ }}B,{\rm{ }}C$ nên $SO \bot \left( {ABCD} \right)$. Ta có $\begin{array}{l}MC \cap \left( {SBD} \right) = S \Rightarrow \dfrac{{d\left( {M;\left( {SBD} \right)} \right)}}{{d\left( {C;\left( {SBD} \right)} \right)}} = \dfrac{{MS}}{{CS}} = \dfrac{1}{2}\\ \Rightarrow d\left( {M;\left( {SBD} \right)} \right) = \dfrac{1}{2}d\left( {C;\left( {SBD} \right)} \right)\end{array}$. Kẻ \(CE \bot BD\) ta có: \(\left\{ \begin{array}{l}CE \bot BD\\CE \bot SO\end{array} \right. \Rightarrow CE \bot \left( {SBD} \right) \Rightarrow d\left( {C;\left( {SBD} \right)} \right) = CE = \dfrac{{CB.CD}}{{\sqrt {C{B^2} + C{D^2}} }} = \dfrac{{a\sqrt 3 }}{2}.\) Vậy \(d\left( {M;\left( {SBD} \right)} \right) = \dfrac{1}{2}CE = \dfrac{{a\sqrt 3 }}{4}\).
Câu 30 :
Cho hình chóp $S.ABC $ có đáy $ABC$ là tam giác vuông tại $B, AB = 3a, BC = 4a.$ Cạnh bên $SA$ vuông góc với đáy. Góc tạo bởi giữa $SC$ và đáy bằng ${60^0}$. Gọi $M$ là trung điểm của $AC,$ tính khoảng cách $d$ giữa hai đường thẳng $AB$ và $SM.$
Đáp án : D Phương pháp giải :
Dựa vào phương pháp xác định mặt phẳng chứa đường thẳng này và song song với đường thẳng kia đưa về tính khoảng cách từ một điểm đến một mặt phẳng Lời giải chi tiết :
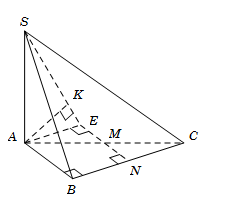 Ta có: \(AC = \sqrt {A{B^2} + B{C^2}} = 5a\) Xác định \({60^0} = \widehat {\left( {SC,\left( {ABC} \right)} \right)} = \widehat {\left( {SC,AC} \right)} = \widehat {SCA}\) và \(SA = AC.\tan \widehat {SCA} = 5a\sqrt 3 .\) Gọi \(N\) là trung điểm \(BC\), suy ra \(MN\parallel AB\). Lấy điểm \(E\) đối xứng với \(N\) qua \(M\), suy ra \(ABNE\) là hình chữ nhật. Do đó $d\left( {AB;SM} \right) = d\left( {AB;\left( {SME} \right)} \right) = d\left( {A;\left( {SME} \right)} \right).$ Kẻ \(AK \bot SE\). Vì \(ME \bot AE,ME \bot SA\) nên \(ME \bot \left( {SAE} \right) \Rightarrow ME \bot AK\) Mà \(AK \bot SE\) nên \(AK \bot \left( {SME} \right)\) Khi đó \(d\left( {A;\left( {SME} \right)} \right) = AK = \dfrac{{SA.AE}}{{\sqrt {S{A^2} + A{E^2}} }} = \dfrac{{10a\sqrt 3 }}{{\sqrt {79} }}.\)
Câu 31 :
Cho hình hộp chữ nhật \(ABCD.A'B'C'D'\) có đáy \(ABCD\) là hình vuông cạnh \(a\sqrt 2 \), \(AA' = 2a\). Tính khoảng cách giữa đường thẳng \(BD\) và mặt phẳng \(\left( {CB'D'} \right)\).
Đáp án : B Phương pháp giải :
Khoảng cách giữa đường thẳng và mặt phẳng song song bằng khoảng cách từ một điểm thuộc đường thẳng này đến mặt phẳng kia. Lời giải chi tiết :
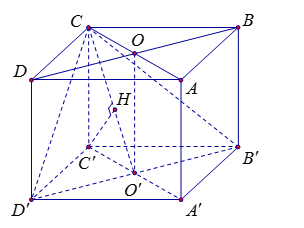 Gọi \(O,\,\)\(O'\) lần lượt là tâm của hai mặt đáy. Khi đó tứ giác \(COO'C'\)là hình bình hành và \(C'O' = \dfrac{{AC}}{2} = a\) Do \(BD\;{\rm{//}}\;B'D'\)$ \Rightarrow BD\;{\rm{//}}\;\left( {CB'D'} \right)$ nên \(d\left( {BD;\left( {CB'D'} \right)} \right) = d\left( {O;\left( {CB'D'} \right)} \right) = d\left( {C';\left( {CB'D'} \right)} \right)\). Ta có : \(\left\{ \begin{array}{l}B'D' \bot A'C'\\B'D' \bot CC'\end{array} \right. \Rightarrow B'D' \bot \left( {COO'C'} \right)\)\( \Rightarrow \left( {CB'D'} \right) \bot \left( {COO'C'} \right)\) Lại có \(\left( {CB'D'} \right) \cap \left( {COO'C'} \right) = CO'\). Trong \(\Delta CC'O'\) hạ \(C'H \bot CO' \Rightarrow C'H \bot \left( {CB'D'} \right)\)\( \Rightarrow d\left( {BD;\,CD'} \right) = C'H\) Khi đó : \(\dfrac{1}{{C'{H^2}}} = \dfrac{1}{{C{{C'}^2}}} + \dfrac{1}{{C'{{O'}^2}}} = \dfrac{1}{{{{\left( {2a} \right)}^2}}} + \dfrac{1}{{{a^2}}} = \dfrac{5}{{4{a^2}}}\)\( \Rightarrow C'H = \dfrac{{2\sqrt 5 a}}{5}\).
Câu 32 :
Xác định giá trị thực \(k\) để hàm số \(f\left( x \right) = \left\{ {\begin{array}{*{20}{l}}{\dfrac{{{x^{2016}} + x - 2}}{{\sqrt {2018x + 1} - \sqrt {x + 2018} }}}&{{\rm{khi}}}&{x \ne 1}\\k&{{\rm{khi}}}&{x = 1}\end{array}} \right.\) liên tục tại \(x = 1\).
Đáp án : B Phương pháp giải :
Hàm số \(y = f\left( x \right)\) liên tục tại \(x = {x_0}\) nếu \(\mathop {\lim }\limits_{x \to {x_0}} f\left( x \right) = f\left( {{x_0}} \right)\) Lời giải chi tiết :
Ta có $\mathop {\lim }\limits_{x \to 1} f\left( x \right) = \mathop {\lim }\limits_{x \to 1} \dfrac{{{x^{2016}} + x - 2}}{{\sqrt {2018x + 1} - \sqrt {x + 2018} }}$ $ = \mathop {\lim }\limits_{x \to 1} \dfrac{{\left( {{x^{2016}} + x - 2} \right)\left( {\sqrt {2018x + 1} + \sqrt {x + 2018} } \right)}}{{2018x + 1 - x - 2018}}$ \( = \mathop {\lim }\limits_{x \to 1} \dfrac{{\left( {x - 1} \right)\left( {{x^{2015}} + {x^{2014}} + ... + x + 2} \right)\left( {\sqrt {2018x + 1} + \sqrt {x + 2018} } \right)}}{{2017\left( {x - 1} \right)}}\) \( = \mathop {\lim }\limits_{x \to 1} \dfrac{{\left( {{x^{2015}} + {x^{2014}} + ... + x + 2} \right)\left( {\sqrt {2018x + 1} + \sqrt {x + 2018} } \right)}}{{2017}} = 2\sqrt {2019} \) Mà \(f\left( 1 \right) = k\) Suy ra hàm số liên tục tại \(x = 1\) \( \Leftrightarrow k = 2\sqrt {2019} \).
Câu 33 :
Cho hình chóp \(S.ABC\) có đáy \(ABC\) là tam giác vuông cân tại \(B\), \(BC = a\), cạnh bên $SA$ vuông góc với đáy, \(SA = a\sqrt 3 \). Gọi \(M\) là trung điểm của \(AC\). Tính côtang góc giữa hai mặt phẳng \(\left( {SBM} \right)\) và \(\left( {SAB} \right)\).
Đáp án : A Phương pháp giải :
- Xác định góc giữa hai mặt phẳng \(\left( {SBM} \right)\) và \(\left( {SAB} \right)\), sử dụng lý thuyết: Góc giữa hai mặt phẳng (không vuông) là góc giữa hai đường thẳng lần lượt thuộc hai mặt phẳng mà vuông góc với giao tuyến. - Tính cô tang góc vừa xác định, sử dụng kiến thức hình học đã biết. Lời giải chi tiết :
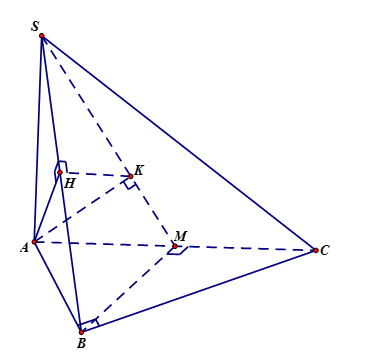 Kẻ \(AH \bot SB\) và \(AK \bot SM\). Vì tam giác \(ABC\) vuông cân tại \(B\)và \(BC = a\)cùng với $SA \bot \left( {ABC} \right)$ nên suy ra \(BM \bot \left( {SAC} \right)\) và \(BM = AM = \dfrac{{AC}}{2} = \dfrac{{a\sqrt 2 }}{2}\). Do đó \(BM \bot AK\). Từ \(BM \bot AK\) và \(AK \bot SM\) suy ra \(AK \bot \left( {SBM} \right)\)\( \Rightarrow AK \bot SB\). Từ \(AH \bot SB\) và \(AK \bot SB\) ta có \(\left( {AHK} \right) \bot SB\). Do đó, góc giữa hai mặt phẳng \(\left( {SBM} \right)\) và \(\left( {SAB} \right)\) bằng hoặc bù với góc \(\widehat {AHK}\). Ta có: $AH = \dfrac{{SA.AB}}{{\sqrt {S{A^2} + A{B^2}} }}$$ = \dfrac{{a.a\sqrt 3 }}{{\sqrt {{{\left( {a\sqrt 3 } \right)}^2} + {a^2}} }}$$ = \dfrac{{a\sqrt 3 }}{2}$. $AK = \dfrac{{SA.AM}}{{\sqrt {S{A^2} + A{M^2}} }}$$ = \dfrac{{\dfrac{{a\sqrt 2 }}{2}.a\sqrt 3 }}{{\sqrt {{{\left( {a\sqrt 3 } \right)}^2} + {{\left( {\dfrac{{a\sqrt 2 }}{2}} \right)}^2}} }}$$ = \dfrac{{a\sqrt {21} }}{7}$. Từ \(\left( {AHK} \right) \bot SB\) ta có \(HK \bot SB\) nên \(\Delta SHK \sim \Delta SMB\), do đó \(\dfrac{{HK}}{{MB}} = \dfrac{{SK}}{{SB}}\). Mặt khác \(SK.SM = S{A^2}\)\( \Rightarrow SK = \dfrac{{S{A^2}}}{{SM}}\)\( = \dfrac{{{{\left( {a\sqrt 3 } \right)}^2}}}{{\sqrt {{{\left( {a\sqrt 3 } \right)}^2} + {{\left( {\dfrac{{a\sqrt 2 }}{2}} \right)}^2}} }}\)\( = \dfrac{{3a\sqrt {14} }}{7}\); \(SB = \sqrt {S{A^2} + A{B^2}} = 2a\); Nên \(\dfrac{{HK}}{{MB}} = \dfrac{{SK}}{{SB}} = \dfrac{{3\sqrt {14} }}{{14}}\)\( \Rightarrow HK = \dfrac{{3\sqrt {14} }}{{14}}.MB\)\( = \dfrac{{3\sqrt {14} }}{{14}}.\dfrac{{a\sqrt 2 }}{2} = \dfrac{{3a\sqrt 7 }}{{14}}\). Trong tam giác \(AHK\) ta có: \(\cos \widehat {AHK} = \dfrac{{A{H^2} + H{K^2} - A{K^2}}}{{2.AH.HK}}\)\( = \dfrac{{{{\left( {\dfrac{{a\sqrt 3 }}{2}} \right)}^2} + {{\left( {\dfrac{{3a\sqrt 7 }}{{14}}} \right)}^2} - {{\left( {\dfrac{{a\sqrt {21} }}{7}} \right)}^2}}}{{2.\dfrac{{a\sqrt 3 }}{2}.\dfrac{{3a\sqrt 7 }}{{14}}}}\)\( = \dfrac{{\sqrt {21} }}{7}\). Như vậy, góc giữa hai mặt phẳng \(\left( {SBM} \right)\) và \(\left( {SAB} \right)\)là \(\alpha \) với \(\cos \alpha = \dfrac{{\sqrt {21} }}{7}\)\( \Rightarrow \sin \alpha = \dfrac{{2\sqrt 7 }}{7}\). Bởi vậy: \(\cot \alpha = \dfrac{{\cos \alpha }}{{\sin \alpha }} = \dfrac{{\sqrt 3 }}{2}\).
Câu 34 :
Biết \(\mathop {\lim }\limits_{x \to + \infty } \left( {\sqrt {4{x^2} - 3x + 1} - \left( {ax + b} \right)} \right) = 0\). Tính \(a - 4b\) ta được
Đáp án : B Phương pháp giải :
- Nhân liên hợp khử dạng vô định \(\infty - \infty \) - Sử dụng điều kiện bài cho để tìm \(a,b\) Lời giải chi tiết :
Ta có $\mathop {\lim }\limits_{x \to + \infty } \left( {\sqrt {4{x^2} - 3x + 1} - \left( {ax + b} \right)} \right) = 0$$ \Leftrightarrow \mathop {\lim }\limits_{x \to + \infty } \left( {\left( {\sqrt {4{x^2} - 3x + 1} - ax} \right) - b} \right) = 0$$ \Leftrightarrow \mathop {\lim }\limits_{x \to + \infty } \left( {\dfrac{{4{x^2} - 3x + 1 - {a^2}{x^2}}}{{\sqrt {4{x^2} - 3x + 1} + ax}} - b} \right) = 0$$ \Leftrightarrow \mathop {\lim }\limits_{x \to + \infty } \left( {\dfrac{{\left( {4 - {a^2}} \right){x^2} - 3x + 1}}{{\sqrt {4{x^2} - 3x + 1} + ax}} - b} \right) = 0$ $ \Leftrightarrow \left\{ \begin{array}{l}4 - {a^2} = 0\\a > 0\\\dfrac{{ - 3}}{{2 + a}} - b = 0\end{array} \right.$$ \Leftrightarrow \left\{ \begin{array}{l}a = 2\\b = - \dfrac{3}{4}\end{array} \right.$. Vậy $a - 4b = 5$.
Câu 35 :
Cho hàm số \(y = f\left( x \right) = \left\{ {\begin{array}{*{20}{l}}{a{x^2} + bx + 1}&{khi}&{x \ge 0}\\{ax - b - 1}&{khi}&{x < 0}\end{array}} \right.\). Khi hàm số \(y = f\left( x \right)\) có đạo hàm tại \({x_0} = 0\), hãy tính \(T = a + 2b\).
Đáp án : C Phương pháp giải :
- Tìm điều kiện để hàm số liên tục tại \({x_0} = 0\) - Tìm điều kiện để hàm số có đạo hàm tại \({x_0} = 0\), điều kiện là \(\mathop {\lim }\limits_{x \to 0} \dfrac{{f\left( x \right) - f\left( 0 \right)}}{x}\) tồn tại. Lời giải chi tiết :
Ta có \(f\left( 0 \right) = 1\). \(\mathop {\lim }\limits_{x \to {0^ + }} f\left( x \right)\) \( = \mathop {\lim }\limits_{x \to {0^ + }} \left( {a{x^2} + bx + 1} \right)\) \( = 1\). \(\mathop {\lim }\limits_{x \to {0^ - }} f\left( x \right)\) \( = \mathop {\lim }\limits_{x \to {0^ - }} \left( {ax - b - 1} \right)\) \( = - b - 1\). Để hàm số có đạo hàm tại \({x_0} = 0\) thì hàm số phải liên tục tại \({x_0} = 0\) nên \(f\left( 0 \right) = \mathop {\lim }\limits_{x \to {0^ + }} f\left( x \right) = \mathop {\lim }\limits_{x \to {0^ - }} f\left( x \right)\). Suy ra \( - b - 1 = 1\)\( \Leftrightarrow b = - 2\). Khi đó \(f\left( x \right) = \left\{ \begin{array}{l}a{x^2} - 2x + 1,x \ge 0\\ax + 1,x < 0\end{array} \right.\). Xét: +) \(\mathop {\lim }\limits_{x \to {0^ + }} \dfrac{{f\left( x \right) - f\left( 0 \right)}}{x}\) \( = \mathop {\lim }\limits_{x \to {0^ + }} \dfrac{{a{x^2} - 2x + 1 - 1}}{x}\)\( = \mathop {\lim }\limits_{x \to {0^ + }} \left( {ax - 2} \right)\)\( = - 2\). +) \(\mathop {\lim }\limits_{x \to {0^ - }} \dfrac{{f\left( x \right) - f\left( 0 \right)}}{x}\) \( = \mathop {\lim }\limits_{x \to {0^ - }} \dfrac{{ax + 1 - 1}}{x}\)\( = \mathop {\lim }\limits_{x \to {0^ - }} \left( a \right)\) \( = a\). Hàm số có đạo hàm tại \({x_0} = 0\)thì \(a = - 2\). Vậy với \(a = - 2\),\(b = - 2\) thì hàm số có đạo hàm tại \({x_0} = 0\) khi đó \(T = - 6\). |