Đề thi học kì 2 Toán 11 - Đề số 4Đề bài
Câu 1 :
Hàm số \(f\left( x \right) = \left\{ \begin{array}{l}\dfrac{{{x^4} + x}}{{{x^2} + x}}\,\,\,khi\,\,x \ne 0,\,x \ne - 1\\3\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,khi\,\,x = - 1\\1\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,khi\,\,x = 0\end{array} \right.\)
Câu 2 :
Cho hình lăng trụ $ABC.A'B'C'$ có đáy $ABC$ là tam giác vuông cân tại $A$ với $BC = a\sqrt 2 $; $AA' = a$ và vuông góc với đáy. Mặt phẳng $\left( \alpha \right)$ qua $M$ là trung điểm của $BC$ và vuông góc với $AB'$. Thiết diện tạo bởi $\left( \alpha \right)$ với hình lăng trụ $ABC.A'B'C'$ là:
Câu 3 :
Cho hình hộp $ABCD.A'B'C'D'$ có đáy là hình thoi $\widehat {BAD} = {60^0}$ và $A'A = A'B = A'D$. Gọi $O = AC \cap BD$. Hình chiếu của $A'$ trên $\left( {ABCD} \right)$ là :
Câu 4 :
Cho hai dãy số \(\left( {{u_n}} \right),\left( {{v_n}} \right)\) với \({u_n} = \dfrac{1}{n},{v_n} = \dfrac{{{{\left( { - 1} \right)}^n}}}{n}\). Biết \(\left| {\dfrac{{{{\left( { - 1} \right)}^n}}}{n}} \right| \le \dfrac{1}{n}\). Chọn kết luận không đúng:
Câu 5 :
Trong các mệnh đề sau đây, mệnh đề nào là đúng?
Câu 6 :
Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình thoi cạnh $a$, các cạnh $SA = SB = a,$ $SD = a\sqrt 2 $. Góc giữa hai mặt phẳng $\left( {SBD} \right)$ và $\left( {ABCD} \right)$ bằng ${90^0}.$ Độ dài đoạn thẳng $BD$
Câu 7 :
Cho hình chóp $S.ABC$ trong đó $SA,{\rm{ }}AB,{\rm{ }}BC$ đôi một vuông góc và $SA = AB = BC = 1.$ Khoảng cách giữa hai điểm $S$ và $C$ nhận giá trị nào trong các giá trị sau ?
Câu 8 :
Cho tứ diện đều \(ABCD\),\(M\) và \(N\) theo thứ tự là trung điểm của cạnh \(AB\) và \(CD\). Mệnh đề nào sau đây sai?
Câu 9 :
Cho hình lăng trụ \(ABC.A'B'C'\) có tất cả các cạnh đều bằng \(a\). Hình chiếu \(H\) của \(A\) trên mặt phẳng \(\left( {A'B'C'} \right)\) thuộc cạnh \(B'C'\). Biết khoảng cách giữa hai mặt phẳng đáy là \(\dfrac{a}{2}\). Tìm vị trí của \(H\) trên \(B'C'\).
Câu 10 :
Giá trị của giới hạn $\mathop {\lim }\limits_{x \to 2} \sqrt[3]{{\dfrac{{{x^2} - x - 1}}{{{x^2} + 2x}}}}$ là:
Câu 11 :
Cho tứ diện \(ABCD\) có \(AB,AC,AD\) đôi một vuông góc. Chỉ ra mệnh đề sai trong các mệnh đề sau:
Câu 12 :
Cho hình chóp $S.ABC$ có đáy \(ABC\) là tam giác vuông tại \(A\), \(\widehat {ABC} = {60^ \circ }\), tam giác \(SBC\) là tam giác đều có cạnh bằng \(2a\). Biết hình chiếu của \(S\) lên mặt phẳng đáy trùng với trung điểm của \(BC\). Tính góc giữa đường thẳng \(SA\) và mặt phẳng đáy \(\left( {ABC} \right)\)
Câu 13 :
Cho hình chóp \(S.ABC\) có đáy \(ABC\) là tam giác vuông tại \(B\), \(AB = a,BC = a\sqrt 3 \). Hình chiếu vuông góc của \(S\) trên mặt đáy là trung điểm \(H\) của cạnh \(AC\). Biết \(SB = a\sqrt 2 \). Tính theo \(a\) khoảng cách từ điểm \(H\) đến mặt phẳng \(\left( {SAB} \right)\)?
Câu 14 :
Cho tứ diện \(ABCD.\) Gọi \(H\) là trực tâm của tam giác \(BCD\) và \(AH\) vuông góc với mặt phẳng đáy. Khẳng định nào dưới đây là đúng ?
Câu 15 :
Cho hình chóp đều $S.ABCD$ có tất cả các cạnh đều bằng $a$. Gọi $\varphi $ là góc giữa hai mặt phẳng $\left( {SBD} \right)$ và $\left( {SCD} \right)$. Mệnh đề nào sau đây đúng?
Câu 16 :
Giá trị của giới hạn $\,\mathop {\lim }\limits_{x \to + \infty } \left( {\sqrt {{x^2} + 3x} - \sqrt {{x^2} + 4x} } \right)$ là:
Câu 17 :
Có tất cả bao nhiêu giá trị nguyên của tham số \(m\) thuộc khoảng \(\left( { - 10;10} \right)\) để phương trình ${x^3} - 3{x^2} + \left( {2m - 2} \right)x + m - 3 = 0$ có ba nghiệm phân biệt ${x_1},{\rm{ }}{x_2},{\rm{ }}{x_3}$ thỏa mãn ${x_1} < - 1 < {x_2} < {x_3}$?
Câu 18 :
Tìm \(m\) để các hàm số \(f(x) = \left\{ \begin{array}{l}\sqrt {2x - 4} + 3 \,\,\, khi \,\,\, x \ge 2\\\dfrac{{x + 1}}{{{x^2} - 2mx + 3m + 2 } } \,\,\, khi \,\,\, x < 2\end{array} \right.\) liên tục trên \(\mathbb{R}\)
Câu 19 :
Trong không gian cho hai tam giác đều $ABC$ và $ABC'$ có chung cạnh $AB$ và nằm trong hai mặt phẳng khác nhau. Gọi $M,{\rm{ }}N,{\rm{ }}P,{\rm{ }}Q$ lần lượt là trung điểm của các cạnh $AC,{\rm{ }}CB,{\rm{ }}BC'$ và $C'A$ . Tứ giác $MNPQ$ là hình gì?
Câu 20 :
Cho hình chóp \(S.ABC\) có đáy \(ABC\) là tam giác đều cạnh \(a\) và độ dài các cạnh bên \(SA = SB = SC = b.\) Gọi \(G\) là trọng tâm của tam giác \(ABC.\) Độ dài đoạn thẳng \(SG\) bằng
Câu 21 :
Cho hình chóp \(S.ABCD\) có \(SA \bot \left( {ABCD} \right)\), đáy \(ABCD\) là hình vuông cạnh \(2a\),\(SA = 2a\sqrt[{}]{3}\). Gọi \(I\) là trung điểm của \(AD\), mặt phẳng \(\left( P \right)\) qua \(I\) và vuông góc với \(SD\). Tính diện tích thiết diện của hình chóp cắt bởi mặt phẳng \(\left( P \right)\).
Câu 22 :
Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình vuông tâm $O$, cạnh $a$. Cạnh bên $SA$ vuông góc với đáy, góc $\widehat {SBD} = {60^0}$. Tính khoảng cách $d$ giữa hai đường thẳng $AB$ và $SO.$
Câu 23 :
Tính $\mathop {\lim }\limits_{x \to 0} \dfrac{{\sqrt {1 + 2x} .\sqrt[3]{{1 + 3x}}.\sqrt[4]{{1 + 4x}} - 1}}{x}$
Câu 24 :
Tìm tất cả các giá trị của tham số \(m\) sao cho phương trình \({x^3} - 3{x^2} + \left( {2m - 2} \right)x + m - 3 = 0\) có ba nghiệm \({x_1}\), \({x_2}\), \({x_3}\) thỏa mãn \({x_1} < - 1 < {x_2} < {x_3}\).
Câu 25 :
Cho hình lập phương \(ABCD.A'B'C'D'\) có cạnh bằng \(a\). Khoảng cách từ ba điểm nào sau đây đến đường chéo \(AC'\) bằng nhau ?
Lời giải và đáp án
Câu 1 :
Hàm số \(f\left( x \right) = \left\{ \begin{array}{l}\dfrac{{{x^4} + x}}{{{x^2} + x}}\,\,\,khi\,\,x \ne 0,\,x \ne - 1\\3\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,khi\,\,x = - 1\\1\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,khi\,\,x = 0\end{array} \right.\)
Đáp án : C Phương pháp giải :
Xét tính liên tục của hàm số tại $x = 0$ và \(x = - 1\) Hàm số \(y = f\left( x \right)\) liên tục tại điểm \(x = {x_0}\) khi và chỉ khi \(\mathop {\lim }\limits_{x \to {x_0}} f\left( x \right) = f\left( {{x_0}} \right)\) Lời giải chi tiết :
Hàm phân thức \(y = \dfrac{{{x^4} + x}}{{{x^2} + x}}\) có txđ \(D = R\backslash \left\{ {0; - 1} \right\}\) và liên tục trên các khoảng \(\left( { - \infty ; - 1} \right),\left( {0; + \infty } \right)\). Ta chỉ cần xét tính liên tục của \(y = f\left( x \right)\) tại các điểm \(x = 0;x = - 1\). Ta có: \(\mathop {\lim }\limits_{x \to - 1} f\left( x \right) = \mathop {\lim }\limits_{x \to - 1} \dfrac{{{x^4} + x}}{{{x^2} + x}} = \mathop {\lim }\limits_{x \to - 1} \dfrac{{{x^3} + 1}}{{x + 1}} = \mathop {\lim }\limits_{x \to - 1} \left( {{x^2} - x + 1} \right) = 3 = f\left( { - 1} \right) \Rightarrow \) Hàm số liên tục tại \(x = - 1\) \(\mathop {\lim }\limits_{x \to 0} f\left( x \right) = \mathop {\lim }\limits_{x \to 0} \dfrac{{{x^4} + x}}{{{x^2} + x}} = \mathop {\lim }\limits_{x \to 0} \dfrac{{{x^3} + 1}}{{x + 1}} = 1 = f\left( 0 \right) \Rightarrow \) Hàm số liên tục tại $x = 0.$ Vậy hàm số liên tục tại mọi điểm \(x \in R\).
Câu 2 :
Cho hình lăng trụ $ABC.A'B'C'$ có đáy $ABC$ là tam giác vuông cân tại $A$ với $BC = a\sqrt 2 $; $AA' = a$ và vuông góc với đáy. Mặt phẳng $\left( \alpha \right)$ qua $M$ là trung điểm của $BC$ và vuông góc với $AB'$. Thiết diện tạo bởi $\left( \alpha \right)$ với hình lăng trụ $ABC.A'B'C'$ là:
Đáp án : B Phương pháp giải :
- Tìm một đường thẳng qua \(M\) và vuông góc với \(\left( {ABB'A'} \right)\) thì đường thẳng đó sẽ vuông góc với \(AB'\). - Sử dụng các tính chất đường thẳng song song mặt phẳng, định lý ba đường giao tuyến để dựng thiết diện cần tìm. - Sử dụng các quan hệ vuông góc, song song để chứng minh thiết diện là hình thang vuông. Lời giải chi tiết :
Gọi N là trung điểm $AB \Rightarrow MN//AC \Rightarrow MN \bot AB$. Ta có $\left\{ \begin{array}{l}MN \bot AB\\MN \bot AA'\end{array} \right. \Rightarrow MN \bot \left( {ABB'A'} \right) \Rightarrow MN \bot AB' \Rightarrow MN \subset \left( \alpha \right).$ Từ giả thiết $ \Rightarrow $$AB = a = AA' \Rightarrow ABB'A'$ là hình vuông $ \Rightarrow BA' \bot AB'$ Trong mp $\left( {ABB'A'} \right)$ kẻ $NQ\parallel BA'$ với $Q \in AA'$. Trong mp $\left( {ACC'A'} \right)$ kẻ $QR\parallel AC$ với $R \in CC'$. Vậy thiết diện là hình thang MNPQ vuông (do MN và QR cùng song song với AC và $MN \bot NQ$). 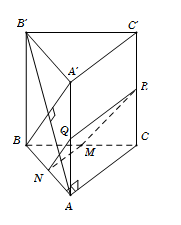
Câu 3 :
Cho hình hộp $ABCD.A'B'C'D'$ có đáy là hình thoi $\widehat {BAD} = {60^0}$ và $A'A = A'B = A'D$. Gọi $O = AC \cap BD$. Hình chiếu của $A'$ trên $\left( {ABCD} \right)$ là :
Đáp án : B Phương pháp giải :
Sử dụng định nghĩa trục đường tròn đáy để tìm hình chiếu của \(A'\) trên mặt đáy Lời giải chi tiết :
Vì $A'A = A'B = A'D \Rightarrow $ hình chiếu của \(A'\) trên $\left( {ABCD} \right)$ trùng với \(H\) là tâm đường tròn ngoại tiếp \(\Delta ABD\,\,\left( 1 \right).\) Mà tứ giác \(ABCD\) là hình thoi và $\widehat {BAD} = {60^0}$ nên \(\Delta BAD\) là tam giác đều \(\left( 2 \right)\) Từ \(\left( 1 \right)\,\)và \(\left( 2 \right) \Rightarrow H\) là trọng tâm \(\Delta ABD\,.\)
Câu 4 :
Cho hai dãy số \(\left( {{u_n}} \right),\left( {{v_n}} \right)\) với \({u_n} = \dfrac{1}{n},{v_n} = \dfrac{{{{\left( { - 1} \right)}^n}}}{n}\). Biết \(\left| {\dfrac{{{{\left( { - 1} \right)}^n}}}{n}} \right| \le \dfrac{1}{n}\). Chọn kết luận không đúng:
Đáp án : D Phương pháp giải :
Cho hai dãy số \(\left( {{u_n}} \right)\) và \(\left( {{v_n}} \right)\). Nếu \(\left| {{u_n}} \right| \le {v_n}\) với mọi \(n\) và \(\lim {v_n} = 0\) thì \(\lim {u_n} = 0\). Lời giải chi tiết :
Dễ thấy \(\lim {u_n} = 0\) nên A đúng. Do \(\left| {\dfrac{{{{\left( { - 1} \right)}^n}}}{n}} \right| \le \dfrac{1}{n}\) và \(\lim \dfrac{1}{n} = 0\) nên \(\lim \dfrac{{{{\left( { - 1} \right)}^n}}}{n} = 0\) hay \(\lim {v_v} = 0\). Do đó các đáp án B và C đúng.
Câu 5 :
Trong các mệnh đề sau đây, mệnh đề nào là đúng?
Đáp án : C Lời giải chi tiết :
Ta có: \(\left\{ \begin{array}{l}a \bot b\\b//c\end{array} \right. \Rightarrow a \bot c\) nên đáp án C đúng.
Câu 6 :
Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình thoi cạnh $a$, các cạnh $SA = SB = a,$ $SD = a\sqrt 2 $. Góc giữa hai mặt phẳng $\left( {SBD} \right)$ và $\left( {ABCD} \right)$ bằng ${90^0}.$ Độ dài đoạn thẳng $BD$
Đáp án : C Phương pháp giải :
Sử dụng phương pháp xác định góc giữa hai mặt phẳng và áp dụng các hệ thức lượng trong tam giác vuông Lời giải chi tiết :
Gọi $I$ là tâm của hình thoi $ABCD$. Và $H$ là hình chiếu vuông góc của $S$ lên $BD$. $\widehat {\left( {\left( {SBD} \right);\left( {ABCD} \right)} \right)} = {90^0} \Rightarrow \left( {SBD} \right) \bot \left( {ABCD} \right) \Rightarrow SH \bot \left( {ABCD} \right)$. Khi đó $\left\{ \begin{array}{l}SH \bot AC\\BD \bot AC\end{array} \right. \Rightarrow AC \bot \left( {SBD} \right) \Rightarrow AC \bot SI$. Mà $I$ là trung điểm của \(AC \Rightarrow \Delta SAC\) cân tại S \( \Rightarrow SA = SB = SC=BC=a\). \(\Delta SAC = \Delta BAC\left( {c.c.c} \right) \Rightarrow BI = SI = \dfrac{1}{2}BD \Rightarrow \Delta SBD\) vuông tại S $ \Rightarrow B{D^2} = S{B^2} + S{D^2} = {a^2} + {\left( {a\sqrt 2 } \right)^2} = 3{a^2} \Rightarrow BD = a\sqrt 3 $. 
Câu 7 :
Cho hình chóp $S.ABC$ trong đó $SA,{\rm{ }}AB,{\rm{ }}BC$ đôi một vuông góc và $SA = AB = BC = 1.$ Khoảng cách giữa hai điểm $S$ và $C$ nhận giá trị nào trong các giá trị sau ?
Đáp án : B Phương pháp giải :
- Chứng minh \(SA \bot \left( {ABC} \right)\) rồi suy ra \(SA \bot AC\) - Sử dụng định lý Pi-ta-go cho tam giác vuông \(SAC\) Lời giải chi tiết :
Do $\left\{ \begin{array}{l}SA \bot AB\\SA \bot BC\end{array} \right.$ nên $SA \bot (ABC) \Rightarrow SA \bot AC$ Như vậy \(SC = \sqrt {S{A^2} + A{C^2}} = \sqrt {S{A^2} + A{B^2} + B{C^2}} = \sqrt 3 \) 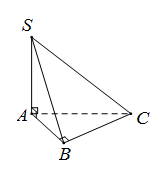
Câu 8 :
Cho tứ diện đều \(ABCD\),\(M\) và \(N\) theo thứ tự là trung điểm của cạnh \(AB\) và \(CD\). Mệnh đề nào sau đây sai?
Đáp án : D Phương pháp giải :
Xét tính đúng, sai của từng đáp án dựa vào công thức trung điểm và các công thức cộng, trừ véc tơ. Lời giải chi tiết :
A.Đúng vì: \(\overrightarrow {AC} + \overrightarrow {BD} = \left( {\overrightarrow {AD} + \overrightarrow {DC} } \right) + \left( {\overrightarrow {BC} + \overrightarrow {CD} } \right) = \overrightarrow {AD} + \overrightarrow {BC} \) B. Đúng vì: \(\overrightarrow {AD} + \overrightarrow {BC} = \left( {\overrightarrow {AM} + \overrightarrow {MN} + \overrightarrow {ND} } \right) + \left( {\overrightarrow {BM} + \overrightarrow {MN} + \overrightarrow {NC} } \right)\)\( = 2\overrightarrow {MN} + \left( {\overrightarrow {AM} + \overrightarrow {BM} } \right) + \left( {\overrightarrow {ND} + \overrightarrow {NC} } \right) = 2\overrightarrow {MN} \) C.Đúng vì: \(\overrightarrow {AC} + \overrightarrow {BD} + \overrightarrow {AD} + \overrightarrow {BC} = 2\overrightarrow {AN} + 2\overrightarrow {BN} = 2\left( {\overrightarrow {AN} + \overrightarrow {BN} } \right) = - 2\left( {\overrightarrow {NA} + \overrightarrow {NB} } \right) = - 4\overrightarrow {NM} \) Vậy D sai. 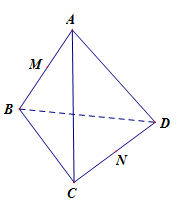
Câu 9 :
Cho hình lăng trụ \(ABC.A'B'C'\) có tất cả các cạnh đều bằng \(a\). Hình chiếu \(H\) của \(A\) trên mặt phẳng \(\left( {A'B'C'} \right)\) thuộc cạnh \(B'C'\). Biết khoảng cách giữa hai mặt phẳng đáy là \(\dfrac{a}{2}\). Tìm vị trí của \(H\) trên \(B'C'\).
Đáp án : B Phương pháp giải :
Từ giả thiết khoảng cách giữa hai mặt đáy, tính được độ dài \(A'H\) và suy ra đáp án. Lời giải chi tiết :
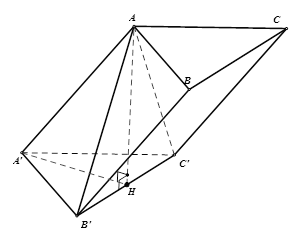 Do hình lăng trụ \(ABC.A'B'C'\) có tất cả các cạnh đều bằng \(a\) nên \(A'A = a\). \(H\) là hình chiếu của \(A\) trên \(\left( {A'B'C'} \right)\) nên \(AH \bot \left( {A'B'C'} \right) \Rightarrow d\left( {\left( {ABC} \right),\left( {A'B'C'} \right)} \right) = AH = \dfrac{a}{2}\) \(\Delta A'HA\) vuông tại \(H\) nên \(A'H = \sqrt {A'{A^2} - A{H^2}} = \sqrt {{a^2} - \dfrac{{{a^2}}}{4}} = \dfrac{{a\sqrt 3 }}{2}\) Mặt khác \(\Delta A'B'C'\) đều cạnh \(a\) nên đường cao \(A'H' = \dfrac{{a\sqrt 3 }}{2}\) ($H'$ là trung điểm của $B'C'$) Từ đó \(A'H = A'H'\) và \(H,H' \in B'C'\) nên \(H \equiv H'\). Vậy \(H\) là trung điểm của \(B'C' \Rightarrow HB' = \dfrac{1}{2}B'C'\).
Câu 10 :
Giá trị của giới hạn $\mathop {\lim }\limits_{x \to 2} \sqrt[3]{{\dfrac{{{x^2} - x - 1}}{{{x^2} + 2x}}}}$ là:
Đáp án : B Phương pháp giải :
Thay \(x = 2\) vào hàm số lấy giới hạn. Lời giải chi tiết :
$\mathop {\lim }\limits_{x \to 2} \sqrt[3]{{\dfrac{{{x^2} - x - 1}}{{{x^2} + 2x}}}} = \sqrt [3]{\dfrac{{{2^2} - 2 - 1}}{{{2^2} + 2.2}}} = \dfrac{1}{2}$
Câu 11 :
Cho tứ diện \(ABCD\) có \(AB,AC,AD\) đôi một vuông góc. Chỉ ra mệnh đề sai trong các mệnh đề sau:
Đáp án : C Phương pháp giải :
Xét tính đúng sai của từng đáp án, sử dụng lý thuyết của hai mặt phẳng vuông góc: Một đường thẳng vuông góc với mặt phẳng này thì mọi mặt phẳng chứa đường thẳng đều vuông góc với mặt phẳng đã cho. Lời giải chi tiết :
\(\begin{array}{l}\left\{ \begin{array}{l}AD \bot AB\\AD \bot AC\end{array} \right. \Rightarrow AD \bot \left( {ABC} \right) \Rightarrow \left( {ACD} \right) \bot \left( {ABC} \right);\left( {ABD} \right) \bot \left( {ABC} \right)\\\left\{ \begin{array}{l}AC \bot AD\\AC \bot AB\end{array} \right. \Rightarrow AC \bot \left( {ABD} \right) \Rightarrow \left( {ACD} \right) \bot \left( {ABD} \right)\end{array}\) \(\Rightarrow \) A đúng. \(AD\bot \left( ABC \right)\Rightarrow AD\bot BC\). Tương tự ta chứng minh được \(AB\bot CD;\,\,AC\bot BD\Rightarrow D\) đúng. Gọi H là trực tâm của tam giác BCD ta có \(\left\{ \begin{align} DH\bot BC \\ AD\bot BC \\ \end{align} \right.\Rightarrow BC\bot \left( ADH \right)\Rightarrow AH\bot BC\) Tương tự ta chứng minh được \(AH\bot BD;\,\,AH\bot CD\Rightarrow AH\bot \left( BCD \right)\) \(\Rightarrow \) B đúng. Chưa đủ điều kiện để kết luận tam giác \(BCD\) vuông.
Câu 12 :
Cho hình chóp $S.ABC$ có đáy \(ABC\) là tam giác vuông tại \(A\), \(\widehat {ABC} = {60^ \circ }\), tam giác \(SBC\) là tam giác đều có cạnh bằng \(2a\). Biết hình chiếu của \(S\) lên mặt phẳng đáy trùng với trung điểm của \(BC\). Tính góc giữa đường thẳng \(SA\) và mặt phẳng đáy \(\left( {ABC} \right)\)
Đáp án : C Phương pháp giải :
Xác định góc giữa đường thẳng và mặt phẳng (khác \({90^0}\)) là góc giữa đường thẳng và hình chiếu của nó trên mặt phẳng. Lời giải chi tiết :
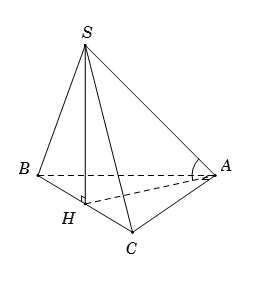 Gọi \(H\) là trung điểm của \(BC\), suy ra \(SH \bot \left( {ABC} \right)\). Vì \(SH \bot \left( {ABC} \right)\) nên \(HA\) là hình chiếu của \(SA\) trên mặt phẳng \(\left( {ABC} \right)\). Do đó \(\widehat {\left( {SA,\left( {ABC} \right)} \right)} = \widehat {\left( {SA,AH} \right)} = \widehat {SAH}\). Tam giác \(SBC\) đều cạnh \(2a\) nên \(SH = a\sqrt 3 .\) Tam giác \(ABC\) vuông tại \(A\) nên \(AH = \dfrac{1}{2}BC = a.\) Tam giác vuông \(SAH\), có \(\tan \widehat {SAH} = \dfrac{{SH}}{{AH}} = \sqrt 3 \), suy ra \(\widehat {SAH} = {60^0}\).
Câu 13 :
Cho hình chóp \(S.ABC\) có đáy \(ABC\) là tam giác vuông tại \(B\), \(AB = a,BC = a\sqrt 3 \). Hình chiếu vuông góc của \(S\) trên mặt đáy là trung điểm \(H\) của cạnh \(AC\). Biết \(SB = a\sqrt 2 \). Tính theo \(a\) khoảng cách từ điểm \(H\) đến mặt phẳng \(\left( {SAB} \right)\)?
Đáp án : B Phương pháp giải :
- Dựng đoạn vuông góc kẻ từ \(H\) đến mặt phẳng \(\left( {SAB} \right)\). - Tính toán dựa vào kiến thức hình học đã biết Lời giải chi tiết :
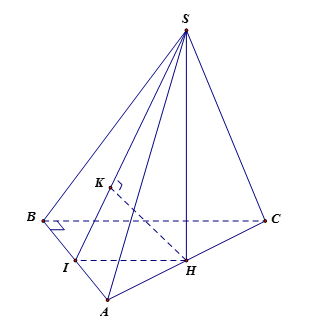 Để tính khoảng cách từ điểm \(H\) đến mặt phẳng \(\left( {SAB} \right)\), ta xác định hình chiếu vuông góc của \(H\) trên mặt phẳng \(\left( {SAB} \right)\) qua các bước sau: - Dựng \(HI \bot AB\) với \(I \in AB\), chứng minh được \(AB \bot \left( {SIH} \right)\) và \(\left( {SIH} \right) \bot \left( {SAB} \right) = SI\). - Dựng \(K\) là hình chiếu vuông góc của \(H\) trên \(SI\), ta chứng minh được \(SK \bot \left( {SAB} \right)\). Vậy \(d\left( {H,\left( {SAB} \right)} \right) = HK\). Do \(HI/{\kern 1pt} /BC\) nên dễ dàng chỉ ra được \(I\) là trung điểm của \(AB\) và \(IH = \dfrac{{BC}}{2} = \dfrac{{a\sqrt 3 }}{2}\), \(IA = IB = \dfrac{{AB}}{2} = \dfrac{a}{2}\). Ta có \(AB \bot SI\) nên \(SI = \sqrt {S{B^2} - I{B^2}} = \sqrt {2{a^2} - \dfrac{{{a^2}}}{4}} = \dfrac{{a\sqrt 7 }}{2}\). Do \(SH \bot IH\) nên xét tam giác vuông \(SIH\) có: \(SH = \sqrt {S{I^2} - I{H^2}} = \sqrt {\dfrac{{7{a^2}}}{4} - \dfrac{{3{a^2}}}{4}} = a\) ; \(HK = \dfrac{{SH.HI}}{{SI}} = \dfrac{{a.\dfrac{{a\sqrt 3 }}{2}}}{{\dfrac{{a\sqrt 7 }}{2}}} = \dfrac{{a\sqrt {21} }}{7}\). Do vậy, ta có \(d\left( {H,\left( {SAB} \right)} \right) = \dfrac{{a\sqrt {21} }}{7}\).
Câu 14 :
Cho tứ diện \(ABCD.\) Gọi \(H\) là trực tâm của tam giác \(BCD\) và \(AH\) vuông góc với mặt phẳng đáy. Khẳng định nào dưới đây là đúng ?
Đáp án : D Phương pháp giải :
Xét tính đúng sai của từng đáp án, sử dụng lý thuyết đường thẳng vuông góc với mặt phẳng thì nó vuông góc với mọi đường thẳng thuộc mặt phẳng và ngược lại. Lời giải chi tiết :
Vì \(AH\) vuông góc với \(mp\,\,\left( {BCD} \right)\) suy ra \(AH \bot CD.\) \(\left( 1 \right)\) Mà \(H\) là trực tâm của tam giác \(BCD\)\( \Rightarrow \,\,BH \bot CD.\) \(\left( 2 \right)\) Từ \(\left( 1 \right),\left( 2 \right)\) suy ra \(\left\{ \begin{array}{l}CD \bot AH\\CD \bot BH\end{array} \right. \Rightarrow CD \bot \left( {ABH} \right) \Rightarrow CD \bot AB.\)
Câu 15 :
Cho hình chóp đều $S.ABCD$ có tất cả các cạnh đều bằng $a$. Gọi $\varphi $ là góc giữa hai mặt phẳng $\left( {SBD} \right)$ và $\left( {SCD} \right)$. Mệnh đề nào sau đây đúng?
Đáp án : D Phương pháp giải :
Sử dụng phương pháp xác định góc giữa hai mặt phẳng và áp dụng các hệ thức lượng trong tam giác vuông Lời giải chi tiết :
Gọi $O = AC \cap BD$. Do hình chóp $S.ABCD$ đều nên $SO \bot \left( {ABCD} \right)$. Gọi $M$ là trung điểm của $SD.$ Tam giác $SCD$ đều nên $CM \bot SD$. Tam giác $SBD$ có $SB = SD = a,$ $BD = a\sqrt 2 $ Suy ra $\Delta \,SBD$ vuông tại $S \Rightarrow SB \bot SD \Rightarrow OM \bot SD.$ Do đó $\left\{ \begin{array}{l}\left( {SBD} \right) \cap \left( {SCD} \right) = SD\\\left( {SBD} \right) \supset OM \bot SD\\\left( {SCD} \right) \supset CM \bot SD\end{array} \right. \Rightarrow \widehat {\left( {\left( {SBD} \right);\left( {SCD} \right)} \right)} = \widehat {\left( {OM;CM} \right)} = \widehat {OMC}.$ Ta có $\left\{ \begin{array}{l}OC \bot BD\\OC \bot SO\end{array} \right. \Rightarrow OC \bot \left( {SBD} \right) \Rightarrow OC \bot OM$. Tam giác vuông MOC vuông tại O, có $\tan \widehat {CMO} = \dfrac{{OC}}{{OM}} = \dfrac{{\dfrac{1}{2}a\sqrt 2 }}{{\dfrac{1}{2}a}} = \sqrt 2 $. 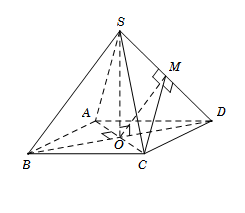
Câu 16 :
Giá trị của giới hạn $\,\mathop {\lim }\limits_{x \to + \infty } \left( {\sqrt {{x^2} + 3x} - \sqrt {{x^2} + 4x} } \right)$ là:
Đáp án : B Phương pháp giải :
Khi \(x \to + \infty \Rightarrow \sqrt {{x^2} + 3x} - \sqrt {{x^2} + 4x} \sim \sqrt {{x^2}} - \sqrt {{x^2}} = 0\) Do đó ta cần nhân lượng liên hợp. Lời giải chi tiết :
\(\mathop {\lim }\limits_{x \to + \infty } \left( {\sqrt {{x^2} + 3x} - \sqrt {{x^2} + 4x} } \right) \) \(= \mathop {\lim }\limits_{x \to + \infty } \dfrac{{ - x}}{{\sqrt {{x^2} + 3x} + \sqrt {{x^2} + 4x} }} \) \(= \mathop {\lim }\limits_{x \to + \infty } \dfrac{{ - 1}}{{\sqrt {1 + \dfrac{3}{x}} + \sqrt {1 + \dfrac{4}{x}} }} = - \dfrac{1}{2}.\)
Câu 17 :
Có tất cả bao nhiêu giá trị nguyên của tham số \(m\) thuộc khoảng \(\left( { - 10;10} \right)\) để phương trình ${x^3} - 3{x^2} + \left( {2m - 2} \right)x + m - 3 = 0$ có ba nghiệm phân biệt ${x_1},{\rm{ }}{x_2},{\rm{ }}{x_3}$ thỏa mãn ${x_1} < - 1 < {x_2} < {x_3}$?
Đáp án : C Phương pháp giải :
- Sử dụng phương pháp điều kiện cần tìm điều kiện của \(m\). - Thay điều kiện dó vào phương trình và kiểm tra lại điều kiện. Lời giải chi tiết :
Xét hàm số $f\left( x \right) = {x^3} - 3{x^2} + \left( {2m - 2} \right)x + m - 3$ liên tục trên $\mathbb{R}$. Giả sử phương trình có ba nghiệm phân biệt ${x_1},{\rm{ }}{x_2},{\rm{ }}{x_3}$ sao cho ${x_1} < - 1 < {x_2} < {x_3}$. Khi đó $f\left( x \right) = \left( {x - {x_1}} \right)\left( {x - {x_2}} \right)\left( {x - {x_3}} \right)$. Ta có $f\left( { - 1} \right) = \left( { - 1 - {x_1}} \right)\left( { - 1 - {x_2}} \right)\left( { - 1 - {x_3}} \right) > 0$ (do ${x_1} < - 1 < {x_2} < {x_3}$). Mà $f\left( { - 1} \right) = - m - 5$ nên suy ra $ - m - 5 > 0 \Leftrightarrow m < - 5.$ Thử lại: Với $m < - 5$, ta có $\mathop {\lim }\limits_{x \to - \infty } f\left( x \right) = - \infty $ nên tồn tại \(a < - 1\) sao cho $f\left( a \right) < 0$. \(\left( 1 \right)\) Do $m < - 5$ nên $f\left( { - 1} \right) = - m - 5 > 0$. \(\left( 2 \right)\) $f\left( 0 \right) = m - 3 < 0$. \(\left( 3 \right)\) $\mathop {\lim }\limits_{x \to + \infty } f\left( x \right) = + \infty $ nên tồn tại \(b > 0\) sao cho $f\left( b \right) > 0$. \(\left( 4 \right)\) Từ \(\left( 1 \right)\) và \(\left( 2 \right)\), suy ra phương trình có nghiệm thuộc khoảng \(\left( { - \infty ; - 1} \right)\); Từ \(\left( 2 \right)\) và \(\left( 3 \right)\), suy ra phương trình có nghiệm thuộc khoảng \(\left( { - 1;0} \right)\); Từ \(\left( 3 \right)\) và \(\left( 4 \right)\), suy ra phương trình có nghiệm thuộc khoảng \(\left( {0; + \infty } \right).\) Vậy khi $m < - 5$ thỏa mãn \(m \in \mathbb{Z},m \in \left( { - 10;10} \right)\) \( \Rightarrow m \in \left\{ { - 9; - 8; - 7; - 6} \right\}.\)
Câu 18 :
Tìm \(m\) để các hàm số \(f(x) = \left\{ \begin{array}{l}\sqrt {2x - 4} + 3 \,\,\, khi \,\,\, x \ge 2\\\dfrac{{x + 1}}{{{x^2} - 2mx + 3m + 2 } } \,\,\, khi \,\,\, x < 2\end{array} \right.\) liên tục trên \(\mathbb{R}\)
Đáp án : C Phương pháp giải :
- Nhận xét tính liên tục của hàm số trên các khoảng \(\left( { - \infty ;2} \right)\) và \(\left( {2; + \infty } \right)\) - Xét tính liên tục của hàm số tại \(x = 2\) và kết luận. Lời giải chi tiết :
Với \(x > 2\) ta có hàm số liên tục. Để hàm số liên tục trên \(\mathbb{R}\) thì hàm số phải liên tục trên khoảng \(\left( { - \infty ;2} \right)\) và liên tục tại \(x = 2\). Hàm số liên tục trên \(\left( { - \infty ;2} \right)\) khi và chỉ khi \(g(x) = {x^2} - 2mx + 3m + 2 \ne 0,{\rm{ }}\forall x \le 2\) TH 1: \(\left\{ \begin{array}{l}\Delta ' = {m^2} - 3m - 2 \le 0\\g(2) = - m + 6 \ne 0\end{array} \right. \) \(\Leftrightarrow \dfrac{{3 - \sqrt {17} }}{2} \le m \le \dfrac{{3 + \sqrt {17} }}{2}\) TH 2:\(\left\{ \begin{array}{l}\Delta ' = {m^2} - 3m - 2 > 0\\{x_1} = m - \sqrt {\Delta '} > 2\end{array} \right. \) \(\Leftrightarrow \left\{ \begin{array}{l}{m^2} - 3m - 2 > 0\\m > 2\\\Delta ' < {(m - 2)^2}\end{array} \right.\) \( \Leftrightarrow \left\{ \begin{array}{l}m > \dfrac{{3 + \sqrt {17} }}{2}\\m < 6\end{array} \right. \) \( \Leftrightarrow \dfrac{{3 + \sqrt {17} }}{2} < m < 6\) Nên \(\dfrac{{3 - \sqrt {17} }}{2} \le m < 6\) (*) thì \(g(x) \ne 0,{\rm{ }}\forall x \le 2\) Lại có: \(\mathop {\lim }\limits_{x \to {2^ + }} f(x) = \mathop {\lim }\limits_{x \to {2^ + }} \left( {\sqrt {2x - 4} + 3} \right) = 3\) \(\mathop {\lim }\limits_{x \to {2^ - }} f(x) = \mathop {\lim }\limits_{x \to {2^ - }} \dfrac{{x + 1}}{{{x^2} - 2mx + 3m + 2}} = \dfrac{3}{{6 - m}}\) Hàm số liên tục tại \(x = 2 \) \(\Leftrightarrow \dfrac{3}{{6 - m}} = 3 \Leftrightarrow m = 5\) (thỏa (*))
Câu 19 :
Trong không gian cho hai tam giác đều $ABC$ và $ABC'$ có chung cạnh $AB$ và nằm trong hai mặt phẳng khác nhau. Gọi $M,{\rm{ }}N,{\rm{ }}P,{\rm{ }}Q$ lần lượt là trung điểm của các cạnh $AC,{\rm{ }}CB,{\rm{ }}BC'$ và $C'A$ . Tứ giác $MNPQ$ là hình gì?
Đáp án : B Phương pháp giải :
Dựng hình, nhận xét tính chất của tứ giác dựa vào các mối quan hệ song song, vuông góc của các đường thẳng. Lời giải chi tiết :
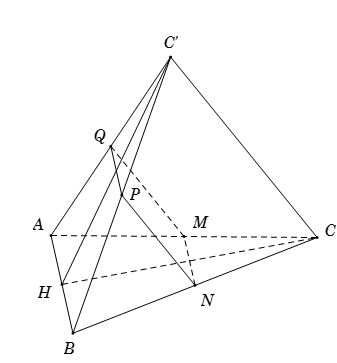 Vì $M,{\rm{ }}N,{\rm{ }}P,{\rm{ }}Q$ lần lượt là trung điểm của các cạnh $AC,{\rm{ }}CB,{\rm{ }}BC'$ và $C'A$ \( \Rightarrow \left\{ \begin{array}{l}PQ = MN = \dfrac{1}{2}AB\\PQ//AB//MN\end{array} \right.\)\( \Rightarrow \) \(MNPQ\) là hình bình hành. Gọi \(H\) là trung điểm của \(AB\). Vì hai tam giác $ABC$ và $ABC'$ đều nên \(\left\{ \begin{array}{l}CH \bot AB\\C'H \bot AB\end{array} \right..\) Suy ra \(AB \bot \left( {CHC'} \right)\). Do đó \(AB \bot CC'\). Ta có \(\left\{ \begin{array}{l}PQ{\rm{//}}AB\\PN{\rm{//}}CC'\\AB \bot CC'\end{array} \right. \Rightarrow PQ \bot PN\) . Vậy tứ giác $MNPQ$là hình chữ nhật.
Câu 20 :
Cho hình chóp \(S.ABC\) có đáy \(ABC\) là tam giác đều cạnh \(a\) và độ dài các cạnh bên \(SA = SB = SC = b.\) Gọi \(G\) là trọng tâm của tam giác \(ABC.\) Độ dài đoạn thẳng \(SG\) bằng
Đáp án : C Phương pháp giải :
Chứng minh \(SG \bot \left( {ABC} \right)\) rồi tính toán dựa vào các kiến thức hình học đã biết. Lời giải chi tiết :
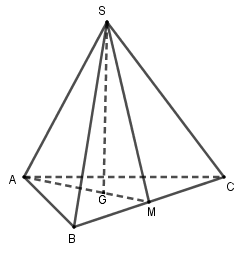 Vì \(SA = SB = SC\) và \(G\) là trọng tâm tam giác \(ABC\) Suy ra \(G\) là chân đường cao kẻ từ đỉnh \(S\) xuống mặt phẳng \(\left( {ABC} \right).\) Gọi \(M\) là trung điểm của \(BC\) suy ra \(BM = CM = \dfrac{{BC}}{2} = \dfrac{a}{2}.\) Tam giác \(ABC\) đều cạnh \(a,\) có \(GM = \dfrac{{AM}}{3} = \dfrac{{a\sqrt 3 }}{2}.\dfrac{1}{3} = \dfrac{{a\sqrt 3 }}{6}.\) Tam giác \(SBM\) vuông tại \(M,\) có \(SM = \sqrt {S{B^2} - M{B^2}} = \sqrt {{b^2} - \dfrac{{{a^2}}}{4}} .\) Tam giác \(SGM\) vuông tại \(G,\) có \(SG = \sqrt {S{M^2} - G{M^2}} = \sqrt {{b^2} - \dfrac{{{a^2}}}{4} - \dfrac{{{a^2}}}{{12}}} = \dfrac{{\sqrt {9{b^2} - 3{a^2}} }}{3}.\)
Câu 21 :
Cho hình chóp \(S.ABCD\) có \(SA \bot \left( {ABCD} \right)\), đáy \(ABCD\) là hình vuông cạnh \(2a\),\(SA = 2a\sqrt[{}]{3}\). Gọi \(I\) là trung điểm của \(AD\), mặt phẳng \(\left( P \right)\) qua \(I\) và vuông góc với \(SD\). Tính diện tích thiết diện của hình chóp cắt bởi mặt phẳng \(\left( P \right)\).
Đáp án : C Phương pháp giải :
- Xác định thiết diện cắt bởi \(\left( P \right)\). - Nhận xét tính chất thiết diện và tính diện tích Lời giải chi tiết :
Kẻ \(IM{\rm{//}}CD\) với \(M \in BC\). Ta có \(\left. \begin{array}{l}IM \bot SA\\IM \bot AD\end{array} \right\}\)\( \Rightarrow IM \bot \left( {SAD} \right)\)\( \Rightarrow IM \bot SD\)\( \Rightarrow \left( P \right) \cap \left( {ABCD} \right) = IM\). Kẻ \(IH \bot SD\) với \(H \in SD\)\( \Rightarrow \left( P \right) \cap \left( {SAD} \right) = IH\). Vì \(\left. \begin{array}{l}IM{\rm{//}}CD\\IM \subset \left( P \right)\\CD \subset \left( {SCD} \right)\end{array} \right\}\)\( \Rightarrow \left( P \right) \cap \left( {SCD} \right) = HK\) với \(HK{\rm{//}}IM\left( {{\rm{//}}CD} \right)\)và \(K \in SC\). \(\left( P \right) \cap \left( {SBC} \right) = KM\). Vì \(IM \bot \left( {SAD} \right)\) nên \(IM \bot IH\). Do đó thiết diện của hình chóp cắt bởi mặt phẳng \(\left( P \right)\) là hình thang \(IHKM\) vuông tại \(I\)và \(H\). Ta có \(IM = AB = 2a\). Xét \(\Delta SAD\) có: \(\tan \widehat {SAD} = \dfrac{{SA}}{{AD}}\)\( = \dfrac{{2\sqrt[{}]{3}a}}{{2a}}\)\( = \sqrt[{}]{3}\)\( \Rightarrow \widehat {SDA} = 60^\circ \). Xét \(\Delta DHI\) có: \(\sin \widehat {HDI} = \dfrac{{HI}}{{ID}}\)\( \Rightarrow HI = ID.\sin 60^\circ \)\( = a.\dfrac{{\sqrt[{}]{3}}}{2}\). Xét \(\Delta SAD\) có: \(SD = \sqrt[{}]{{S{A^2} + A{D^2}}}\)\( = \sqrt[{}]{{12{a^2} + 4{a^2}}}\)\( = 4a\). Xét \(\Delta DHI\) có: \(HD = \sqrt[{}]{{I{D^2} - I{H^2}}}\)\( = \sqrt[{}]{{{a^2} - \dfrac{{3{a^2}}}{4}}}\)\( = \dfrac{a}{2}\)\( \Rightarrow SH = SD - HD\)\( = 4a - \dfrac{a}{2}\)\( = \dfrac{{7a}}{2}\). Vì \(HK{\rm{//}}CD\) nên theo Talet ta có \(\dfrac{{HK}}{{CD}} = \dfrac{{SH}}{{SD}}\)\( = \dfrac{{\dfrac{{7a}}{2}}}{{4a}} = \dfrac{7}{8}\)\( \Rightarrow HK = \dfrac{7}{8}CD\)\( = \dfrac{7}{8}.2a\)\( = \dfrac{{7a}}{4}\). Do đó diện tích thiết diện là \({S_{IHKM}} = \dfrac{{\left( {IM + HK} \right).IH}}{2}\)\( = \dfrac{{\left( {2a + \dfrac{{7a}}{4}} \right).\dfrac{{a\sqrt[{}]{3}}}{2}}}{2}\)\( = \dfrac{{15\sqrt[{}]{3}{a^2}}}{{16}}\).
Câu 22 :
Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình vuông tâm $O$, cạnh $a$. Cạnh bên $SA$ vuông góc với đáy, góc $\widehat {SBD} = {60^0}$. Tính khoảng cách $d$ giữa hai đường thẳng $AB$ và $SO.$
Đáp án : D Phương pháp giải :
Dựa vào phương pháp xác định mặt phẳng chứa đường thẳng này và song song với đường thẳng kia đưa về tính khoảng cách từ một điểm đến một mặt phẳng Lời giải chi tiết :
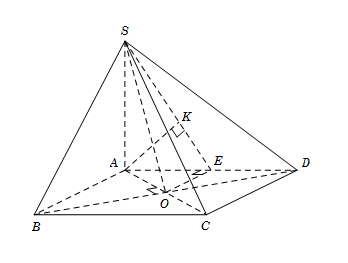 Ta có \(\Delta \,SAB = \Delta \,SAD\) \(\left( {c - g - c} \right)\), suy ra \(SB = SD\). Mà $\widehat {SBD} = {60^0}$$ \Rightarrow $\(\Delta \,SBD\) đều cạnh \(SB = SD = BD = a\sqrt 2 \). Tam giác vuông \(SAB\), có \(SA = \sqrt {S{B^2} - A{B^2}} = a\). Gọi \(E\) là trung điểm \(AD\), suy ra \(OE\parallel AB\) và \(AE \bot OE\). Do đó \(d\left( {AB;SO} \right) = d\left( {AB;\left( {SOE} \right)} \right) = d\left( {A;\left( {SOE} \right)} \right).\) Kẻ \(AK \bot SE\,\,\,\left( 1 \right)\)ta có: \(\left\{ \begin{array}{l}OE \bot AD\\OE \bot SA\end{array} \right. \Rightarrow OE \bot \left( {SAD} \right) \Rightarrow OE \bot AK\,\,\left( 2 \right)\) Từ (1) và (2) \( \Rightarrow AK \bot \left( {SOE} \right)\) \( \Rightarrow d\left( {A;\left( {SOE} \right)} \right) = AK = \dfrac{{SA.AE}}{{\sqrt {S{A^2} + A{E^2}} }} = \dfrac{{a\sqrt 5 }}{5}\)
Câu 23 :
Tính $\mathop {\lim }\limits_{x \to 0} \dfrac{{\sqrt {1 + 2x} .\sqrt[3]{{1 + 3x}}.\sqrt[4]{{1 + 4x}} - 1}}{x}$
Đáp án : D Phương pháp giải :
- Biến đổi biểu thức, đưa về dạng $\mathop {\lim }\limits_{x \to 0} \dfrac{{\sqrt[n]{{1 + nx}} - 1}}{x}$ - Nhân liên hợp. Lời giải chi tiết :
Ta có: $\begin{array}{l}\sqrt {1 + 2x} .\sqrt[3]{{1 + 3x}}.\sqrt[4]{{1 + 4x}} - 1\\ = \sqrt {1 + 2x} - \sqrt {1 + 2x} + \sqrt {1 + 2x} .\sqrt[3]{{1 + 3x}} - \sqrt {1 + 2x} .\sqrt[3]{{1 + 3x}} + \sqrt {1 + 2x} .\sqrt[3]{{1 + 3x}}.\sqrt[4]{{1 + 4x}} - 1\\ = \left( {\sqrt {1 + 2x} - 1} \right) + \sqrt {1 + 2x} \left( {\sqrt[3]{{1 + 3x}} - 1} \right) + \sqrt {1 + 2x} .\sqrt[3]{{1 + 3x}}.\left( {\sqrt[4]{{1 + 4x}} - 1} \right)\end{array}$ $\begin{array}{l} \Rightarrow \mathop {\lim }\limits_{x \to 0} \dfrac{{\sqrt {1 + 2x} .\sqrt[3]{{1 + 3x}}.\sqrt[4]{{1 + 4x}} - 1}}{x}\\ = \mathop {\lim }\limits_{x \to 0} \left( {\dfrac{{\sqrt {1 + 2x} - 1}}{x}} \right) + \mathop {\lim }\limits_{x \to 0} \left( {\sqrt {1 + 2x} .\dfrac{{\sqrt[3]{{1 + 3x}} - 1}}{x}} \right) + \mathop {\lim }\limits_{x \to 0} \left( {\sqrt {1 + 2x} .\sqrt[3]{{1 + 3x}}.\dfrac{{\sqrt[4]{{1 + 4x}} - 1}}{x}} \right)\end{array}$ Tính: $\mathop {\lim }\limits_{x \to 0} \left( {\dfrac{{\sqrt {1 + 2x} - 1}}{x}} \right) = \mathop {\lim }\limits_{x \to 0} \dfrac{{\left( {\sqrt {1 + 2x} - 1} \right)\left( {\sqrt {1 + 2x} + 1} \right)}}{{x\left( {\sqrt {1 + 2x} + 1} \right)}} = \mathop {\lim }\limits_{x \to 0} \dfrac{{2x}}{{x\left( {\sqrt {1 + 2x} + 1} \right)}} = \mathop {\lim }\limits_{x \to 0} \dfrac{2}{{\sqrt {1 + 2x} + 1}} = \dfrac{2}{{1 + 1}} = 1$ $\begin{array}{l}\mathop {\lim }\limits_{x \to 0} \left( {\sqrt {1 + 2x} .\dfrac{{\sqrt[3]{{1 + 3x}} - 1}}{x}} \right) = \mathop {\lim }\limits_{x \to 0} \left( {\sqrt {1 + 2x} .\dfrac{{\left( {\sqrt[3]{{1 + 3x}} - 1} \right)\left[ {{{\left( {\sqrt[3]{{1 + 3x}}} \right)}^2} + \sqrt[3]{{1 + 3x}} + 1} \right]}}{{x.\left[ {{{\left( {\sqrt[3]{{1 + 3x}}} \right)}^2} + \sqrt[3]{{1 + 3x}} + 1} \right]}}} \right)\\ = \mathop {\lim }\limits_{x \to 0} \left( {\sqrt {1 + 2x} .\dfrac{{3x}}{{x.\left[ {{{\left( {\sqrt[3]{{1 + 3x}}} \right)}^2} + \sqrt[3]{{1 + 3x}} + 1} \right]}}} \right) = \mathop {\lim }\limits_{x \to 0} \left( {\dfrac{{3\sqrt {1 + 2x} }}{{\left[ {{{\left( {\sqrt[3]{{1 + 3x}}} \right)}^2} + \sqrt[3]{{1 + 3x}} + 1} \right]}}} \right) = \dfrac{{3.1}}{{1 + 1 + 1}} = 1\end{array}$ $\begin{array}{l}\mathop {\lim }\limits_{x \to 0} \left( {\sqrt {1 + 2x} .\sqrt[3]{{1 + 3x}}.\dfrac{{\sqrt[4]{{1 + 4x}} - 1}}{x}} \right) = \mathop {\lim }\limits_{x \to 0} \left( {\sqrt {1 + 2x} .\sqrt[3]{{1 + 3x}}.\dfrac{{\left( {\sqrt[4]{{1 + 4x}} - 1} \right)\left[ {{{\left( {\sqrt[4]{{1 + 4x}}} \right)}^3} + {{\left( {\sqrt[4]{{1 + 4x}}} \right)}^2} + \sqrt[4]{{1 + 4x}} + 1} \right]}}{{x\left[ {{{\left( {\sqrt[4]{{1 + 4x}}} \right)}^3} + {{\left( {\sqrt[4]{{1 + 4x}}} \right)}^2} + \sqrt[4]{{1 + 4x}} + 1} \right]}}} \right)\\ = \mathop {\lim }\limits_{x \to 0} \left( {\sqrt {1 + 2x} .\sqrt[3]{{1 + 3x}}.\dfrac{{4x}}{{x\left[ {{{\left( {\sqrt[4]{{1 + 4x}}} \right)}^3} + {{\left( {\sqrt[4]{{1 + 4x}}} \right)}^2} + \sqrt[4]{{1 + 4x}} + 1} \right]}}} \right)\\ = \mathop {\lim }\limits_{x \to 0} \dfrac{{4\sqrt {1 + 2x} .\sqrt[3]{{1 + 3x}}}}{{{{\left( {\sqrt[4]{{1 + 4x}}} \right)}^3} + {{\left( {\sqrt[4]{{1 + 4x}}} \right)}^2} + \sqrt[4]{{1 + 4x}} + 1}} = \dfrac{{4.1.1}}{{1 + 1 + 1 + 1}} = 1\end{array}$ Vậy $\mathop {\lim }\limits_{x \to 0} \dfrac{{\sqrt {1 + 2x} .\sqrt[3]{{1 + 3x}}.\sqrt[4]{{1 + 4x}} - 1}}{x} = 1 + 1 + 1 = 3$
Câu 24 :
Tìm tất cả các giá trị của tham số \(m\) sao cho phương trình \({x^3} - 3{x^2} + \left( {2m - 2} \right)x + m - 3 = 0\) có ba nghiệm \({x_1}\), \({x_2}\), \({x_3}\) thỏa mãn \({x_1} < - 1 < {x_2} < {x_3}\).
Đáp án : B Phương pháp giải :
- Sử dụng phương pháp điều kiện cần, điều kiện đủ, từ giả thiết có ba nghiệm thỏa mãn \({x_1} < - 1 < {x_2} < {x_3}\) suy ra điều kiện của \(m\) - Thử lại với \(m\) vừa tìm được và kết luận. Lời giải chi tiết :
Đặt \(f\left( x \right) = {x^3} - 3{x^2} + \left( {2m - 2} \right)x + m - 3\). Ta thấy hàm số liên tục trên \(\mathbb{R}\). Dễ thấy nếu \(x \to - \infty \)thì \(f\left( x \right) \to - \infty \) hay \(f\left( x \right) < 0\) Suy ra điều kiện cần để \(f\left( x \right) = 0\) có \(3\) nghiệm thỏa \({x_1} < - 1 < {x_2} < {x_3}\) là $f\left( { - 1} \right) > 0 \Leftrightarrow - m - 5 > 0 \Leftrightarrow m < - 5$. Điều kiện đủ: với \(m < - 5\) ta có *) \(\mathop {\lim }\limits_{x \to - \infty } f\left( x \right) = - \infty \) nên tồn tại \(a < - 1\) sao cho \(f\left( a \right) < 0\) Mặt khác \(f\left( { - 1} \right) = - m - 5 > 0\). Suy ra \(f\left( a \right).f\left( { - 1} \right) < 0\). Do đó tồn tại \({x_1} \in \left( {a; - 1} \right)\) sao cho \(f\left( {{x_1}} \right) = 0\). *) \(f\left( 0 \right) = m - 3 < 0\), \(f\left( { - 1} \right) > 0\). Suy ra \(f\left( 0 \right).f\left( { - 1} \right) < 0\). Do đó tồn tại \({x_2} \in \left( { - 1;0} \right)\) sao cho \(f\left( {{x_2}} \right) = 0\). *) \(\mathop {\lim }\limits_{x \to + \infty } f\left( x \right) = + \infty \) nên tồn tại \(b > 0\) sao cho \(f\left( b \right) > 0\) Mặt khác \(f\left( 0 \right) < 0\). Suy ra \(f\left( 0 \right).f\left( b \right) < 0\). Do đó tồn tại \({x_3} \in \left( {0;b} \right)\) sao cho \(f\left( {{x_3}} \right) = 0\). Vậy \(m < - 5\) thỏa mãn yêu cầu bài toán.
Câu 25 :
Cho hình lập phương \(ABCD.A'B'C'D'\) có cạnh bằng \(a\). Khoảng cách từ ba điểm nào sau đây đến đường chéo \(AC'\) bằng nhau ?
Đáp án : B Phương pháp giải :
Tìm các tam giác vuông bằng nhau có cùng cạnh huyền $AC'$ và kết luận đáp án đúng. Lời giải chi tiết :
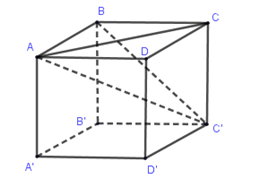 Dễ thấy các tam giác $ABC',C'CA,ADC'$ là các tam giác vuông bằng nhau nên các đường cao hạ từ đỉnh góc vuông xuống cạnh huyền cũng bằng nhau. Vậy: $d\left( {B,AC'} \right) = d\left( {C,AC'} \right) = d\left( {D,AC'} \right)$ |