Đề thi học kì 2 Toán 11 - Đề số 2Đề bài
Câu 1 :
Cho hình chóp \(S.ABC\) có \(AB = AC\) và \(\widehat {SAC} = \widehat {SAB}\). Tính số đo của góc giữa hai đường thẳng chéo nhau \(SA\) và \(BC.\)
Câu 2 :
Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình thang vuông tại $A$ và $D$, đáy lớn $AB$; cạnh bên $SA$ vuông góc với đáy. Gọi $Q$ là điểm trên cạnh $SA$ và $Q \ne A,$ $Q \ne S$; $M$ là điểm trên đoạn $AD$ và $M \ne A$. Mặt phẳng $\left( \alpha \right)$ qua $QM$ và vuông góc với mặt phẳng $\left( {SAD} \right)$. Thiết diện tạo bởi $\left( \alpha \right)$ với hình chóp đã cho là:
Câu 3 :
Trong các mệnh đề sau, mệnh đề nào đúng?
Câu 4 :
Trong các mệnh đề sau, mệnh đề nào sai?
Câu 5 :
Cho hàm số \(y = \sin x\). Chọn câu sai ?
Câu 6 :
Cho hàm số \(y = {\left( {{x^2} - 1} \right)^2}.\) Tính giá trị biểu thức \(M = {y^{\left( 4 \right)}} + 2xy''' - 4y''.\)
Câu 7 :
Chọn đáp án đúng: Với \(c,k\) là các hằng số và \(k\) nguyên dương thì:
Câu 8 :
Tính $\mathop {\lim }\limits_{x \to - 1} \dfrac{{{x^2} + 6x + 5}}{{{x^3} + 2{x^2} - 1}}$ bằng?
Câu 9 :
Giới hạn $\lim \dfrac{{{{\left( {2 - 5n} \right)}^3}{{\left( {n + 1} \right)}^2}}}{{2 - 25{n^5}}}$bằng?
Câu 10 :
Giá trị của giới hạn \(\mathop {\lim }\limits_{x \to + \infty } \left( {\sqrt {{x^2} + 1} + x} \right)\) là:
Câu 11 :
Giá trị của giới hạn $\mathop {\lim }\limits_{x \to 2} \sqrt[3]{{\dfrac{{{x^2} - x - 1}}{{{x^2} + 2x}}}}$ là:
Câu 12 :
Giới hạn $\lim \dfrac{{{2^{n + 1}} - {{3.5}^n} + 5}}{{{{3.2}^n} + {{9.5}^n}}}$bằng?
Câu 13 :
Cho hình chóp $S.ABC$ có đáy $ABC$ là tam giác đều cạnh $a$. Cạnh bên $SA = a\sqrt 3 $ và vuông góc với mặt đáy $\left( {ABC} \right)$. Tính khoảng cách $d$ từ $A$ đến mặt phẳng $\left( {SBC} \right)$.
Câu 14 :
Cho hàm số \(f\left( x \right) = \sqrt[3]{x}\). Giá trị của \(f'\left( 8 \right)\) bằng:
Câu 15 :
Cho hình chóp đều $S.ABCD$ có tất cả các cạnh đều bằng $a$. Gọi $\varphi $ là góc giữa hai mặt phẳng $\left( {SBD} \right)$ và $\left( {SCD} \right)$. Mệnh đề nào sau đây đúng?
Câu 16 :
Trong các mệnh đề sau mệnh đề nào đúng?
Câu 17 :
Trong không gian tập hợp các điểm \(M\) cách đều hai điểm cố định \(A\) và \(B\) là
Câu 18 :
Hàm số \(y = {\left( {{x^2} + 1} \right)^3}\) có đạo hàm cấp ba là:
Câu 19 :
Tiếp tuyến của đồ thị hàm số hàm số \(y = 2{x^3} + 3{x^2}\) tại điểm có tung độ bằng $5$ có phương trình là?
Câu 20 :
Viết phương trình tiếp tuyến $d$ của đồ thị hàm số \(y = {x^3} - 3{x^2} + 2\) tại điểm có hoành độ \({x_0}\) thỏa mãn \(f''\left( {{x_0}} \right) = 0?\)
Câu 21 :
Giả sử \(\mathop {\lim }\limits_{x \to {x_0}} f\left( x \right) = L,\mathop {\lim }\limits_{x \to {x_0}} g\left( x \right) = M\), khi đó:
Câu 22 :
Cho hàm số \(f\left( x \right)\) xác định trên $\left( {0; + \infty } \right)$ bởi $f\left( x \right) = \dfrac{1}{x}$. Đạo hàm của \(f\left( x \right)\) tại ${x_0} = \sqrt 2 $ là
Câu 23 :
Biết rằng$\mathop {\lim }\limits_{x \to - \sqrt 3 } \dfrac{{2{x^3} + 6\sqrt 3 }}{{3 - {x^2}}} = a\sqrt 3 + b.$ Tính \({a^2} + {b^2}.\)
Câu 24 :
Cho hình chóp $S.ABC$ có đáy $ABC$ là tam giác vuông cạnh huyền $BC = a$. Hình chiếu vuông góc của \(S\) lên $\left( {ABC} \right)$ trùng với trung điểm$BC$. Biết $SB = a$. Tính số đo của góc giữa $SA$ và $\left( {ABC} \right)$.
Câu 25 :
Biết rằng \(f\left( x \right) = \left\{ {\begin{array}{*{20}{l}}{\dfrac{{{x^2} - 1}}{{\sqrt x - 1}}}&{{\rm{khi }}x \ne 1}\\a&{{\rm{khi }}x = 1}\end{array}} \right.\) liên tục trên đoạn \(\left[ {0;1} \right]\) (với \(a\) là tham số). Khẳng định nào dưới đây về giá trị \(a\) là đúng?
Câu 26 :
Cho hình lập phương \(ABCD.A'B'C'D'\) có cạnh bằng \(a\). Khoảng cách từ đỉnh \(A\) của hình lập phương đó đến đường thẳng \(CD'\) bằng
Câu 27 :
Đạo hàm của hàm số \(y = \dfrac{1}{{x\sqrt x }}\) là:
Câu 28 :
Cho tứ diện \(OABC\) có \(OA,{\rm{ }}OB,{\rm{ }}OC\) đôi một vuông góc với nhau. Gọi \(H\) là hình chiếu của \(O\) trên mặt phẳng \(\left( {ABC} \right)\). Mệnh đề nào sau đây là sai?
Câu 29 :
Cho dãy số $({u_n})$ với ${u_n} = \dfrac{1}{{1.3}} + \dfrac{1}{{3.5}} + ... + \dfrac{1}{{\left( {2n - 1} \right).\left( {2n + 1} \right)}}$ Khi đó $\lim {u_n}$ bằng?
Câu 30 :
Tính đạo hàm của hàm số sau: \(f\left( x \right) = \left\{ \begin{array}{l}{x^2} - 3x + 1\,\,\,\,khi\,\,x > 1\\2x + 2\,\,\,\,\,\,\,\,\,\,\,\,\,khi\,\,x \le 1\end{array} \right.\) ta được:
Câu 31 :
Tính $\mathop {\lim }\limits_{x \to - \infty } \left( {\sqrt {{x^2} + 1} + x - 1} \right)$ bằng?
Câu 32 :
Tính$\mathop {\lim }\limits_{x \to - \infty } (x - 1)\sqrt {\dfrac{{{x^2}}}{{2{x^4} + {x^2} + 1}}} $ bằng?
Câu 33 :
Cho hàm số \(f\left( x \right)\) xác định trên $[a; b].$ Trong các khẳng định sau, khẳng định nào đúng?
Câu 34 :
Cho hàm số \(f\left( x \right) = \left\{ \begin{array}{l}\dfrac{{\sqrt {{{\left( {x - 3} \right)}^2}} }}{{x - 3}}\,\,khi\,\,x \ne 3\\m\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,khi\,x = 3\end{array} \right.\). Tìm tất cả các giá trị của tham số thực $m$ để hàm số liên tục tại $x = 3.$
Câu 35 :
Cho hàm số \(f\left( x \right) = {x^3} - 3{x^2} + 1\). Đạo hàm của hàm số f(x) âm khi và chỉ khi
Câu 36 :
Cho hàm số \(y = \dfrac{{x - 3}}{{x + 4}}\) có đạo hàm là $y'$ và $y''$. Mệnh đề nào sau đây đúng?
Câu 37 :
Số tiếp tuyến đi qua điểm \(A\left( {1; - 6} \right)\) của đồ thị hàm số \(y = {x^3} - 3x + 1\) là:
Câu 38 :
Số tiếp tuyến của đồ thị hàm số \(y = \dfrac{1}{3}{x^3} - 2{x^2} + 3x + 1\) song song với đường thẳng \(y = 8x + 2\) là:
Câu 39 :
Cho hình chóp $S.ABCD$ có đáy là hình vuông $ABCD$ cạnh bằng $a$ và các cạnh bên đều bằng $a$. Gọi $M$ và $N$ lần lượt là trung điểm của $AD$ và $SD$. Số đo của góc $\left( {MN,SC} \right)$ bằng:
Câu 40 :
Cho hình chóp $S.ABC$ có \(SA \bot (ABC)\) và tam giác $ABC$ không vuông, gọi $H,{\rm{ }}K$ lần lượt là trực tâm các tam giác$ABC$ và $SBC$. Các đường thẳng $AH,{\rm{ }}SK,{\rm{ }}BC$ thỏa mãn:
Câu 41 :
Cho hình chóp $S.ABC$ thỏa mãn $SA{\rm{ }} = {\rm{ }}SB{\rm{ }} = {\rm{ }}SC$. Tam giác $ABC$ vuông tại $A$. Gọi $H$ là hình chiếu vuông góc của $S$ lên $mp\left( {ABC} \right)$. Chọn khẳng định sai trong các khẳng định sau?
Câu 42 :
Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình chữ nhật tâm $O$ với $AB = a,$ $AD = 2a.$ Cạnh bên $SA = a$ và vuông góc với đáy. Gọi $\left( \alpha \right)$ là mặt phẳng qua $SO$ và vuông góc với $\left( {SAD} \right).$ Tính diện tích $S$ của thiết diện tạo bởi $\left( \alpha \right)$ và hình chóp đã cho.
Câu 43 :
Trong mặt phẳng $\left( P \right)$ cho nửa đường tròn đường kính $AB = 2R$ và điểm $C$ thuộc nửa đường tròn đó sao cho $AC = R$. Trên đường thẳng vuông góc với $\left( P \right)$ tại $A$ lấy điểm $S$ sao cho góc giữa hai mặt phẳng $\left( {SAB} \right)$ và $\left( {SBC} \right)$ bằng ${60^0}$. Gọi $H,\,\,K$ lần lượt là hình chiếu của $A$ lên $SB,\,\,SC$. Độ dài cạnh $SA$ tính theo $R$ là
Câu 44 :
Cho tứ diện $SABC$ trong đó$SA$, $SB$, $SC$ vuông góc với nhau từng đôi một và$SA = 3a$, $SB = a$,$SC = 2a$. Khoảng cách từ $A$ đến đường thẳng $BC$ bằng:
Câu 45 :
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình chữ nhật với \(AB = a,{\rm{ }}AD = 2a\). Cạnh bên \(SA\) vuông góc với đáy, góc giữa \(SD\) với đáy bằng \({60^0}.\) Tính khoảng cách \(d\) từ điểm \(C\) đến mặt phẳng \(\left( {SBD} \right)\) theo \(a\).
Câu 46 :
Cho hình chóp $S.ABC $ có đáy $ABC$ là tam giác vuông tại $B, AB = 3a, BC = 4a.$ Cạnh bên $SA$ vuông góc với đáy. Góc tạo bởi giữa $SC$ và đáy bằng ${60^0}$. Gọi $M$ là trung điểm của $AC,$ tính khoảng cách $d$ giữa hai đường thẳng $AB$ và $SM.$
Câu 47 :
Cho hình hộp chữ nhật $ABCD.A’B’C’D’$ có đáy $ABCD$ là hình vuông cạnh \(a\sqrt 2 \), $AA’ = 2a$. Tính khoảng cách $d$ giữa hai đường thẳng $BD$ và $CD’$.
Câu 48 :
Cho hình chóp \(S.ABDC\), với đáy \(ABCD\) là hình bình hành tâm \(O;AD,SA,AB\) đôi một vuông góc \(AD = 8,SA = 6\). \((P)\)là mặt phẳng qua trung điểm của \(AB\) và vuông góc với \(AB\). Thiết diện của \((P)\) và hình chóp có diện tích bằng?
Câu 49 :
Cho \(a, b\) là các số thực khác \(0\). Tìm hệ thức liên hệ giữa \(a\) và \(b\) để hàm số sau liên tục tại \(x = 0\): \(f\left( x \right) = \left\{ \begin{array}{l}\dfrac{{\sqrt {ax + 1} \sqrt[3]{{bx + 1}} - 1}}{x}\,\,\,\,\,khi\,x \ne 0\\a + b\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,khi\,\,x = 0\end{array} \right.\)
Câu 50 :
Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình chữ nhật, $BC = a$. Cạnh bên $SA$ vuông góc với đáy, góc $\widehat {SCA} = \widehat {BSC} = {30^0}$. Gọi $M$ là trung điểm của $CD$. Tính khoảng cách từ $D$ đến mặt phẳng $\left( {SAM} \right)$.
Lời giải và đáp án
Câu 1 :
Cho hình chóp \(S.ABC\) có \(AB = AC\) và \(\widehat {SAC} = \widehat {SAB}\). Tính số đo của góc giữa hai đường thẳng chéo nhau \(SA\) và \(BC.\)
Đáp án : D Phương pháp giải :
Tính tích vô hướng \(\overrightarrow {SA} .\overrightarrow {BC} \) rồi suy ra đáp án. Lời giải chi tiết :
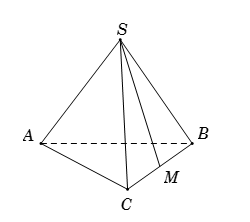 Xét \(\overrightarrow {SA} .\overrightarrow {BC} = \overrightarrow {SA} .\left( {\overrightarrow {SC} - \overrightarrow {SB} } \right) = \overrightarrow {SA} .\overrightarrow {SC} - \overrightarrow {SA} .\overrightarrow {SB} \) $ = \left| {\overrightarrow {SA} } \right|.\left| {\overrightarrow {SC} } \right|.\cos \left( {\overrightarrow {SA} ,\overrightarrow {SC} } \right) - \left| {\overrightarrow {SA} } \right|.\left| {\overrightarrow {SB} } \right|.\cos \widehat {SAB}$ $ = SA.SC.\cos \widehat {ASC} - SA.SB.\cos \widehat {ASB}.$ \(\left( 1 \right)\) Ta có \(\left\{ \begin{array}{l}SA{\rm{ chung}}\\AB = AC\\\widehat {SAB} = \widehat {SAC}\end{array} \right. \Rightarrow \Delta SAB = \Delta SAC{\rm{ }}\left( {c - g - c} \right)\). Suy ra \(\left\{ \begin{array}{l}SC = SB\\\widehat {ASC} = \widehat {ASB}\end{array} \right.\). \(\left( 2 \right)\) Từ \(\left( 1 \right)\) và \(\left( 2 \right)\), suy ra \(\overrightarrow {SA} .\overrightarrow {BC} = 0\). Vậy \(SA \bot BC\).
Câu 2 :
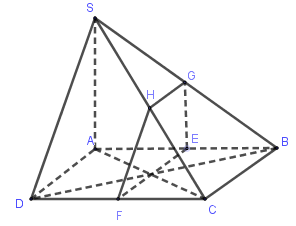
Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình thang vuông tại $A$ và $D$, đáy lớn $AB$; cạnh bên $SA$ vuông góc với đáy. Gọi $Q$ là điểm trên cạnh $SA$ và $Q \ne A,$ $Q \ne S$; $M$ là điểm trên đoạn $AD$ và $M \ne A$. Mặt phẳng $\left( \alpha \right)$ qua $QM$ và vuông góc với mặt phẳng $\left( {SAD} \right)$. Thiết diện tạo bởi $\left( \alpha \right)$ với hình chóp đã cho là:
Đáp án : C Lời giải chi tiết :
 Ta có $\left\{ \begin{array}{l}AB \bot AD\\AB \bot SA\end{array} \right. \Rightarrow AB \bot \left( {SAD} \right)$. Mà $\left( \alpha \right) \bot \left( {SAD} \right)$ suy ra $AB\parallel \left( \alpha \right)$. Qua $M$ kẻ đường thẳng song song với $AB$ cắt $BC$ tại $N$. Qua $Q$ kẻ đường thẳng song song với $AB$ cắt $SB$ tại $P$. Khi đó thiết diện là hình thang $MNPQ$ (do \(MN\parallel PQ\)). Vì $AB \bot \left( {SAD} \right)$ suy ra $MN \bot \left( {SAD} \right)$ nên $MN \bot MQ$. Do đó thiết diện $MNPQ$ là hình thang vuông tại Q và $M$.
Câu 3 :
Trong các mệnh đề sau, mệnh đề nào đúng?
Đáp án : A Phương pháp giải :
Xét tính đúng sai của từng đáp án dựa vào tính chất đường vuông góc chung của hai đường thẳng chéo nhau. Lời giải chi tiết :
Đáp án A: Đúng Đáp án B: Sai, do phát biểu này thiếu yếu tố "đường vuông góc chung phải cắt nhau với hai đường thẳng đã cho". Đáp án C: Sai, vì "mặt phẳng đi qua đường thẳng này và vuông góc với đường thẳng kia" chưa chắc đã tồn tại. Đáp án D: Sai, do phát biểu này thiếu yếu tố vuông góc.
Câu 4 :
Trong các mệnh đề sau, mệnh đề nào sai?
Đáp án : C Phương pháp giải :
Sử dụng các định nghĩa, tính chất về khoảng cách giữa hai mặt phẳng song song, hai đường thẳng chéo nhau, đường thẳng và mặt phẳng song song. Lời giải chi tiết :
Khoảng cách giữa hai đường thẳng chéo nhau $a$ và $b$ là khoảng cách từ một điểm $M$ thuộc đường thẳng $b$ đến mặt phẳng $(P)$ chứa $a$ và song song với $b$ chứ không phải khoảng cách giữa hai điểm như đáp án C nói nên C sai.
Câu 5 :
Cho hàm số \(y = \sin x\). Chọn câu sai ?
Đáp án : D Phương pháp giải :
Tính đạo hàm cấp một, hai, ba, biến đổi các công thức lượng giác và suy ra đáp án sai. Lời giải chi tiết :
\(y' = \cos x = \sin \left( {x + \dfrac{\pi }{2}} \right) \Rightarrow \) Đáp án A đúng. \(y'' = - \sin x = \sin \left( {x + \pi } \right) \Rightarrow \) Đáp án B đúng. \(y''' = - \cos x = \sin \left( {x + \dfrac{{3\pi }}{2}} \right) \Rightarrow \) Đáp án C đúng.
Câu 6 :
Cho hàm số \(y = {\left( {{x^2} - 1} \right)^2}.\) Tính giá trị biểu thức \(M = {y^{\left( 4 \right)}} + 2xy''' - 4y''.\)
Đáp án : C Phương pháp giải :
Khai triển hàm số về dạng hàm đa thức rồi tính các đạo hàm từ cấp 1 đến cấp 4, thay vào biểu thức \(M\) và kết luận. Lời giải chi tiết :
Hàm số viết lại: \(y = {x^4} - 2{x^2} + 1\). Ta có \(y' = 4{x^3} - 4x\), \(y'' = 12{x^2} - 4\), \(y''' = 24x\), \({y^{\left( 4 \right)}} = 24\). Khi đó \(M = {y^{\left( 4 \right)}} + 2xy''' - 4y'' = 24 + 2x.24x - 4\left( {12{x^2} - 4} \right) = 40.\)
Câu 7 :
Chọn đáp án đúng: Với \(c,k\) là các hằng số và \(k\) nguyên dương thì:
Đáp án : A Lời giải chi tiết :
Ta có: \(\mathop {\lim }\limits_{x \to \pm \infty } c = c,\mathop {\lim }\limits_{x \to \pm \infty } \dfrac{c}{{{x^k}}} = 0\) nên đáp án A đúng.
Câu 8 :
Tính $\mathop {\lim }\limits_{x \to - 1} \dfrac{{{x^2} + 6x + 5}}{{{x^3} + 2{x^2} - 1}}$ bằng?
Đáp án : C Phương pháp giải :
- Rút gọn phân thức. - Khử dạng $\dfrac{0}{0}$. Lời giải chi tiết :
$\mathop {\lim }\limits_{x \to - 1} \dfrac{{{x^2} + 6x + 5}}{{{x^3} + 2{x^2} - 1}} = \mathop {\lim }\limits_{x \to - 1} \dfrac{{(x + 1)(x + 5)}}{{(x + 1)({x^2} + x - 1)}} = \mathop {\lim }\limits_{x \to - 1} \dfrac{{x + 5}}{{{x^2} + x - 1}} = \dfrac{{ - 1 + 5}}{{{{( - 1)}^2} + ( - 1) - 1}} = - 4$
Câu 9 :
Giới hạn $\lim \dfrac{{{{\left( {2 - 5n} \right)}^3}{{\left( {n + 1} \right)}^2}}}{{2 - 25{n^5}}}$bằng?
Đáp án : C Phương pháp giải :
Chia cả tử mẫu của phân thức cho ${n^5}$. Lời giải chi tiết :
$\lim \dfrac{{{{(2 - 5n)}^3}{{(n + 1)}^2}}}{{2 - 25{n^5}}}$ $ = \lim \dfrac{{\dfrac{{{{(2 - 5n)}^3}}}{{{n^3}}}.\dfrac{{{{(n + 1)}^2}}}{{{n^2}}}}}{{\dfrac{{2 - 25{n^5}}}{{{n^5}}}}}$ $ = \dfrac{{{{\left( {\frac{{2 - 5n}}{n}} \right)}^3}.{{\left( {\frac{{n + 1}}{n}} \right)}^2}}}{{\frac{2}{{{n^5}}} - 25}}$ $ = \lim \dfrac{{{{\left( {\dfrac{2}{n} - 5} \right)}^3}.{{\left( {1 + \dfrac{1}{n}} \right)}^2}}}{{\dfrac{2}{{{n^5}}} - 25}} $ $ = \dfrac{{{{\left( {0 - 5} \right)}^3}{{\left( {1 + 0} \right)}^2}}}{{0 - 25}}$ $= \dfrac{{{{( - 5)}^3}{{.1}^2}}}{{ - 25}} = 5$.
Câu 10 :
Giá trị của giới hạn \(\mathop {\lim }\limits_{x \to + \infty } \left( {\sqrt {{x^2} + 1} + x} \right)\) là:
Đáp án : B Phương pháp giải :
Đặt \(x\) làm nhân tử chung. Lời giải chi tiết :
\(\mathop {\lim }\limits_{x \to + \infty } \left( {\sqrt {{x^2} + 1} + x} \right) = \mathop {\lim }\limits_{x \to + \infty } x\left( {\sqrt {1 + \dfrac{1}{{{x^2}}}} + 1} \right) = + \infty \) vì \(\left\{ \begin{array}{l}\mathop {\lim }\limits_{x \to + \infty } x = + \infty \\\mathop {\lim }\limits_{x \to + \infty} \sqrt {1 + \dfrac{1}{{{x^2}}}} + 1 = 2 > 0\end{array} \right..\)
Câu 11 :
Giá trị của giới hạn $\mathop {\lim }\limits_{x \to 2} \sqrt[3]{{\dfrac{{{x^2} - x - 1}}{{{x^2} + 2x}}}}$ là:
Đáp án : B Phương pháp giải :
Thay \(x = 2\) vào hàm số lấy giới hạn. Lời giải chi tiết :
$\mathop {\lim }\limits_{x \to 2} \sqrt[3]{{\dfrac{{{x^2} - x - 1}}{{{x^2} + 2x}}}} = \sqrt [3]{\dfrac{{{2^2} - 2 - 1}}{{{2^2} + 2.2}}} = \dfrac{1}{2}$
Câu 12 :
Giới hạn $\lim \dfrac{{{2^{n + 1}} - {{3.5}^n} + 5}}{{{{3.2}^n} + {{9.5}^n}}}$bằng?
Đáp án : D Phương pháp giải :
Bước 1: Chia cả tử mẫu của phân thức cho ${5^n}$. Bước 2: Sử dụng giới hạn \(\lim {q^n} = 0\) nếu \(\left| q \right| < 1\). Lời giải chi tiết :
Bước 1: $\lim \dfrac{{{2^{n + 1}} - {{3.5}^n} + 5}}{{{{3.2}^n} + {{9.5}^n}}}$ $ = \lim \dfrac{{{{2.2}^n} - {{3.5}^n} + 5}}{{{{3.2}^n} + {{9.5}^n}}} $ $= \lim \dfrac{{2.{{\left( {\dfrac{2}{5}} \right)}^n} - 3 + 5.{{\left( {\dfrac{1}{5}} \right)}^n}}}{{3.{{\left( {\dfrac{2}{5}} \right)}^n} + 9}}$ Bước 2: $ =\dfrac{2.0-3+5.0}{3.0+9}= \dfrac{{ - 3}}{9} = - \dfrac{1}{3}.$
Câu 13 :
Cho hình chóp $S.ABC$ có đáy $ABC$ là tam giác đều cạnh $a$. Cạnh bên $SA = a\sqrt 3 $ và vuông góc với mặt đáy $\left( {ABC} \right)$. Tính khoảng cách $d$ từ $A$ đến mặt phẳng $\left( {SBC} \right)$.
Đáp án : A Phương pháp giải :
Sử dụng phương pháp kẻ chân đường cao từ điểm đến mặt phẳng (lý thuyết đường thẳng vuông góc với mặt phẳng) để xác định khoảng cách từ một điểm đến mặt phẳng Lời giải chi tiết :
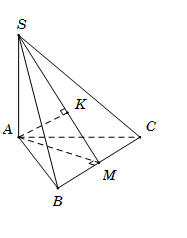 Gọi M là trung điểm BC, suy ra $AM \bot BC$ và $AM = \dfrac{{a\sqrt 3 }}{2}$. Gọi K là hình chiếu của A trên SM, suy ra $AK \bot SM$. $\left( 1 \right)$ Ta có $\left\{ \begin{array}{l}AM \bot BC\\BC \bot SA\end{array} \right. \Rightarrow BC \bot \left( {SAM} \right) \Rightarrow BC \bot AK.$ $\left( 2 \right)$ Từ (1) và (2), suy ra $AK \bot \left( {SBC} \right)$ nên $d\left( {A;\left( {SBC} \right)} \right) = AK.$ Trong $\Delta \,SAM$, có $AK = \dfrac{{SA.AM}}{{\sqrt {S{A^2} + A{M^2}} }} = \dfrac{{3a}}{{\sqrt {15} }} = \dfrac{{a\sqrt {15} }}{5}.$ Vậy $d\left( {A;\left( {SBC} \right)} \right) = AK = \dfrac{{a\sqrt {15} }}{5}.$
Câu 14 :
Cho hàm số \(f\left( x \right) = \sqrt[3]{x}\). Giá trị của \(f'\left( 8 \right)\) bằng:
Đáp án : B Phương pháp giải :
+) Đưa hàm số về dạng \({x^n}\) và áp dụng công thức \(\left( {{x^n}} \right)' = n{x^{n - 1}}\) +) Thay $x = 8$ và tính \(f'\left( 8 \right)\) Lời giải chi tiết :
\(f\left( x \right) = \sqrt[3]{x} = {x^{\frac{1}{3}}} \Rightarrow f'\left( x \right) = \dfrac{1}{3}.{x^{\frac{1}{3} - 1}} = \dfrac{1}{3}{x^{ - \frac{2}{3}}} = \dfrac{1}{3}\dfrac{1}{{{x^{\frac{2}{3}}}}} = \dfrac{1}{3}\dfrac{1}{{\sqrt[3]{{{x^2}}}}}\) \(\Rightarrow f'\left( 8 \right) = \dfrac{1}{3}.\dfrac{1}{{\sqrt[3]{{{8^2}}}}} = \dfrac{1}{{12}}\)
Câu 15 :
Cho hình chóp đều $S.ABCD$ có tất cả các cạnh đều bằng $a$. Gọi $\varphi $ là góc giữa hai mặt phẳng $\left( {SBD} \right)$ và $\left( {SCD} \right)$. Mệnh đề nào sau đây đúng?
Đáp án : D Phương pháp giải :
Sử dụng phương pháp xác định góc giữa hai mặt phẳng và áp dụng các hệ thức lượng trong tam giác vuông Lời giải chi tiết :
Gọi $O = AC \cap BD$. Do hình chóp $S.ABCD$ đều nên $SO \bot \left( {ABCD} \right)$. Gọi $M$ là trung điểm của $SD.$ Tam giác $SCD$ đều nên $CM \bot SD$. Tam giác $SBD$ có $SB = SD = a,$ $BD = a\sqrt 2 $ Suy ra $\Delta \,SBD$ vuông tại $S \Rightarrow SB \bot SD \Rightarrow OM \bot SD.$ Do đó $\left\{ \begin{array}{l}\left( {SBD} \right) \cap \left( {SCD} \right) = SD\\\left( {SBD} \right) \supset OM \bot SD\\\left( {SCD} \right) \supset CM \bot SD\end{array} \right. \Rightarrow \widehat {\left( {\left( {SBD} \right);\left( {SCD} \right)} \right)} = \widehat {\left( {OM;CM} \right)} = \widehat {OMC}.$ Ta có $\left\{ \begin{array}{l}OC \bot BD\\OC \bot SO\end{array} \right. \Rightarrow OC \bot \left( {SBD} \right) \Rightarrow OC \bot OM$. Tam giác vuông MOC vuông tại O, có $\tan \widehat {CMO} = \dfrac{{OC}}{{OM}} = \dfrac{{\dfrac{1}{2}a\sqrt 2 }}{{\dfrac{1}{2}a}} = \sqrt 2 $. 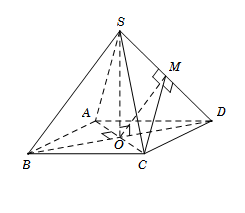
Câu 16 :
Trong các mệnh đề sau mệnh đề nào đúng?
Đáp án : B Phương pháp giải :
Sử dụng các định nghĩa, tính chất của góc giữa đường thẳng và mặt phẳng để xét tính đúng, sai cho từng đáp án. Lời giải chi tiết :
Đáp án A sai vì nếu trường hợp đường thẳng vuông góc với mặt phẳng thì định nghĩa đó không còn đúng. Đáp án C sai vì \(\left( P \right)\) và \(\left( Q \right)\) có thể trùng nhau. Đáp án D sai vì \(a,b\) có thể trùng nhau.
Câu 17 :
Trong không gian tập hợp các điểm \(M\) cách đều hai điểm cố định \(A\) và \(B\) là
Đáp án : A Lời giải chi tiết :
Mặt phẳng trung trực của đoạn thẳng là tập hợp các điểm cách đều hai đầu mút của đoạn thẳng đó
Câu 18 :
Hàm số \(y = {\left( {{x^2} + 1} \right)^3}\) có đạo hàm cấp ba là:
Đáp án : C Phương pháp giải :
Cách 1: Sử dụng đạo hàm của hàm số hợp tính lần lượt đạo hàm cấp một, cấp hai, cấp ba. Cách 2: Sử dụng hằng đẳng thức \({\left( {a + b} \right)^3} = {a^3} + 3{a^2}b + 3a{b^2} + {b^3}\) trước khi tính đạo hàm. Lời giải chi tiết :
Cách 1: \(\begin{array}{l}y' = 3{\left( {{x^2} + 1} \right)^2}\left( {{x^2} + 1} \right)' = 6x{\left( {{x^2} + 1} \right)^2}\\y'' = 6{\left( {{x^2} + 1} \right)^2} + 6x.2\left( {{x^2} + 1} \right).2x\\\,\,\,\,\,\, = 6{\left( {{x^2} + 1} \right)^2} + 24{x^2}\left( {{x^2} + 1} \right)\\y''' = 12\left( {{x^2} + 1} \right).2x + 24.2x.\left( {{x^2} + 1} \right) + 24{x^2}.2x\\\,\,\,\,\,\,\, = 24x\left( {{x^2} + 1} \right) + 48x\left( {{x^2} + 1} \right) + 48{x^3}\\\,\,\,\,\,\, = 24x\left( {{x^2} + 1 + 2\left( {{x^2} + 1} \right) + 2{x^2}} \right) = 24x\left( {5{x^2} + 3} \right)\end{array}\) Cách 2: \(\begin{array}{l}y = {\left( {{x^2} + 1} \right)^3} = {x^6} + 3{x^4} + 3{x^2} + 1\\y' = 6{x^5} + 12{x^3} + 6x\\y'' = 30{x^4} + 36{x^2} + 6\\y''' = 120{x^3} + 72x = 24x\left( {5{x^2} + 3} \right)\end{array}\)
Câu 19 :
Tiếp tuyến của đồ thị hàm số hàm số \(y = 2{x^3} + 3{x^2}\) tại điểm có tung độ bằng $5$ có phương trình là?
Đáp án : A Phương pháp giải :
- Tìm điểm thuộc đồ thị hàm số có tung độ bằng $5$. - Phương trình tiếp tuyến của \(\left( C \right)\) tại điểm \(M\left( {{x_o};{y_0}} \right)\) là: \(y = f'\left( {{x_0}} \right)\left( {x - {x_0}} \right) + {y_0}\) Lời giải chi tiết :
\(\begin{array}{l}y = 5 \Leftrightarrow 2{x^3} + 3{x^2} = 5 \Leftrightarrow x = 1 \Rightarrow \left( C \right) \cap Oy = M\left( {1;5} \right)\\y' = 6{x^2} + 6x \Rightarrow y'\left( 1 \right) = 12\end{array}\) \( \Rightarrow \) Phương trình tiếp tuyến của đồ thị hàm số tại điểm \(M\left( {1;5} \right)\) là: \(y = 12\left( {x - 1} \right) + 5 = 12x - 7\)
Câu 20 :
Viết phương trình tiếp tuyến $d$ của đồ thị hàm số \(y = {x^3} - 3{x^2} + 2\) tại điểm có hoành độ \({x_0}\) thỏa mãn \(f''\left( {{x_0}} \right) = 0?\)
Đáp án : A Phương pháp giải :
- Tìm điểm có hoành độ \({x_0}\) thuộc đồ thị hàm số. - Phương trình tiếp tuyến của \(\left( C \right)\) tại điểm \(M\left( {{x_o};{y_0}} \right)\) là: \(y = f'\left( {{x_0}} \right)\left( {x - {x_0}} \right) + {y_0}\) Lời giải chi tiết :
\(\begin{array}{l}y = f\left( x \right) = {x^3} - 3{x^2} + 2\\f'\left( x \right) = 3{x^2} - 6x,f''\left( x \right) = 6x - 6 = 0 \Leftrightarrow x = 1 \Rightarrow y = 0 \Rightarrow M\left( {1;0} \right)\end{array}\) \(y'\left( 1 \right) = - 3 \Rightarrow \) Phương trình tiếp tuyến của đồ thị hàm số tại \(M\left( {1;0} \right)\) là \(y = - 3\left( {x - 1} \right) + 0 \Leftrightarrow 3x + y - 3 = 0\)
Câu 21 :
Giả sử \(\mathop {\lim }\limits_{x \to {x_0}} f\left( x \right) = L,\mathop {\lim }\limits_{x \to {x_0}} g\left( x \right) = M\), khi đó:
Đáp án : D Lời giải chi tiết :
Giả sử \(\mathop {\lim }\limits_{x \to {x_0}} f\left( x \right) = L,\mathop {\lim }\limits_{x \to {x_0}} g\left( x \right) = M\). Khi đó: \(\mathop {\lim }\limits_{x \to {x_0}} \left[ {f\left( x \right) + g\left( x \right)} \right] = L + M\)
Câu 22 :
Cho hàm số \(f\left( x \right)\) xác định trên $\left( {0; + \infty } \right)$ bởi $f\left( x \right) = \dfrac{1}{x}$. Đạo hàm của \(f\left( x \right)\) tại ${x_0} = \sqrt 2 $ là
Đáp án : B Phương pháp giải :
Sử dụng định nghĩa: Hàm số \(y = f\left( x \right)\) được gọi là có đạo hàm tại \(x = {x_0}\), kí hiệu \(f'\left( {{x_0}} \right)\) nếu giới hạn $\mathop {\lim }\limits_{x \to {x_0}} \dfrac{{f\left( x \right) - f\left( {{x_0}} \right)}}{{x - {x_0}}} = \mathop {\lim }\limits_{\Delta x \to 0} \dfrac{{\Delta y}}{{\Delta x}} = f'\left( {{x_0}} \right)$ tồn tại hữu hạn. Lời giải chi tiết :
Giả sử \(\Delta x\) là số gia của đối số tại \({x_0}\). Ta có \(\Delta y = f\left( {{x_0} + \Delta x} \right) - f\left( {{x_0}} \right)\)\( = \dfrac{1}{{{x_0} + \Delta x}} - \dfrac{1}{{{x_0}}}\)\( = - \dfrac{{\Delta x}}{{{x_0}\left( {{x_0} + \Delta x} \right)}}\). \(\mathop {\lim }\limits_{\Delta x \to 0} \dfrac{{\Delta y}}{{\Delta x}} = \mathop {\lim }\limits_{\Delta x \to 0} \left( { - \dfrac{1}{{{x_0}\left( {{x_0} + \Delta x} \right)}}} \right) = - \dfrac{1}{{x_0^2}}\). Vậy $f'\left( {{x_0}} \right) = - \dfrac{1}{{x_0^2}}$$ \Rightarrow f'\left( {\sqrt 2 } \right) = - \dfrac{1}{2}$.
Câu 23 :
Biết rằng$\mathop {\lim }\limits_{x \to - \sqrt 3 } \dfrac{{2{x^3} + 6\sqrt 3 }}{{3 - {x^2}}} = a\sqrt 3 + b.$ Tính \({a^2} + {b^2}.\)
Đáp án : A Phương pháp giải :
Đưa tử và mẫu của phân thức về dạng tích, khử dạng vô định và tính giới hạn. Lời giải chi tiết :
Ta có $\mathop {\lim }\limits_{x \to - \sqrt 3 } \dfrac{{2({x^3} + 3\sqrt 3 )}}{{3 - {x^2}}}$ $ = \mathop {\lim }\limits_{x \to - \sqrt 3 } \dfrac{{2\left( {x + \sqrt 3 } \right)\left( {{x^2} - \sqrt 3 x + 3} \right)}}{{\left( {\sqrt 3 - x} \right)\left( {\sqrt 3 + x} \right)}}$ $ = \mathop {\lim }\limits_{x \to - \sqrt 3 } \dfrac{{2\left( {{x^2} - \sqrt 3 x + 3} \right)}}{{\sqrt 3 - x}}$ $ = \dfrac{{2\left[ {{{\left( { - \sqrt 3 } \right)}^2} - \sqrt 3 .\left( { - \sqrt 3 } \right) + 3} \right]}}{{\sqrt 3 - \left( { - \sqrt 3 } \right)}} = \dfrac{{18}}{{2\sqrt 3 }} = 3\sqrt 3 $ $ \Rightarrow \left\{ \begin{array}{l}a = 3\\b = 0\end{array} \right. \Rightarrow {a^2} + {b^2} = 9$.
Câu 24 :
Cho hình chóp $S.ABC$ có đáy $ABC$ là tam giác vuông cạnh huyền $BC = a$. Hình chiếu vuông góc của \(S\) lên $\left( {ABC} \right)$ trùng với trung điểm$BC$. Biết $SB = a$. Tính số đo của góc giữa $SA$ và $\left( {ABC} \right)$.
Đáp án : C Phương pháp giải :
- Xác định góc giữa \(SA\) và \(\left( {ABC} \right)\) bởi định nghĩa: là góc giữa \(SA\) và hình chiếu của nó trên \(\left( {ABC} \right)\). - Tính góc tìm được ở trên, sử dụng các tỉ số lượng giác trong tam giác vuông. Lời giải chi tiết :
Gọi \(H\) là trung điểm của \(BC\) suy ra \(AH = BH = CH = \dfrac{1}{2}BC = \dfrac{a}{2}\). Ta có: \(SH \bot \left( {ABC} \right) \Rightarrow SH = \sqrt {S{B^2} - B{H^2}} = \dfrac{{a\sqrt 3 }}{2}\) \(\widehat {\left( {SA,\left( {ABC} \right)} \right)} = \widehat {\left( {SA,HA} \right)} = \widehat {SAH} = \alpha \) $ \Rightarrow \tan \alpha = \dfrac{{SH}}{{AH}} = \sqrt 3 \Rightarrow \alpha = 60^\circ $.
Câu 25 :
Biết rằng \(f\left( x \right) = \left\{ {\begin{array}{*{20}{l}}{\dfrac{{{x^2} - 1}}{{\sqrt x - 1}}}&{{\rm{khi }}x \ne 1}\\a&{{\rm{khi }}x = 1}\end{array}} \right.\) liên tục trên đoạn \(\left[ {0;1} \right]\) (với \(a\) là tham số). Khẳng định nào dưới đây về giá trị \(a\) là đúng?
Đáp án : A Phương pháp giải :
Hàm số \(y = f\left( x \right)\) liên tục trên \(\left( {a;b} \right]\) nếu nó liên tục trên \(\left( {a;b} \right)\) và \(\mathop {\lim }\limits_{x \to {b^ - }} f\left( x \right) = f\left( b \right)\) Lời giải chi tiết :
Hàm số xác định và liên tục trên \(\left[ {0;1} \right)\). Khi đó \(f\left( x \right)\) liên tục trên \(\left[ {0;1} \right]\) khi và chỉ khi \(\mathop {\lim }\limits_{x \to {1^ - }} f\left( x \right) = f\left( 1 \right).{\rm{ }}\left( * \right)\) Ta có \(\left\{ \begin{array}{l}f\left( 1 \right) = a\\\mathop {\lim }\limits_{x \to {1^ - }} f\left( x \right) = \mathop {\lim }\limits_{x \to {1^ - }} \dfrac{{{x^2} - 1}}{{\sqrt x - 1}} = \mathop {\lim }\limits_{x \to {1^ - }} \left[ {\left( {x + 1} \right)\left( {\sqrt x + 1} \right)} \right] = 4\end{array} \right.\) \( \Rightarrow \left( * \right) \Leftrightarrow a = 4\)
Câu 26 :
Cho hình lập phương \(ABCD.A'B'C'D'\) có cạnh bằng \(a\). Khoảng cách từ đỉnh \(A\) của hình lập phương đó đến đường thẳng \(CD'\) bằng
Đáp án : B Phương pháp giải :
Gọi \(M\) là trung điểm của \(CD'\), chứng minh \(AM \bot CD'\) và tính độ dài \(AM\). Lời giải chi tiết :
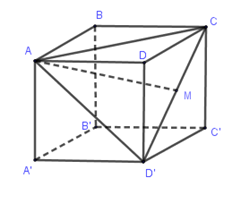 Gọi $M$ là trung điểm của $CD'$. Do \(ABCD.A'B'C'D'\)là hình lập phương nên tam giác $ACD'$là tam giác đều cạnh \(a\sqrt 2 \). $AM \bot CD' \Rightarrow d\left( {A,CD'} \right) = AM = \dfrac{{a\sqrt 6 }}{2}$
Câu 27 :
Đạo hàm của hàm số \(y = \dfrac{1}{{x\sqrt x }}\) là:
Đáp án : D Phương pháp giải :
Đưa hàm số về dạng \({x^n}\) và áp dụng công thức \(\left( {{x^n}} \right)' = n{x^{n - 1}}\) Lời giải chi tiết :
\(\begin{array}{l}y = \dfrac{1}{{x\sqrt x }} = \dfrac{1}{{x.{x^{\frac{1}{2}}}}} = \dfrac{1}{{{x^{1 + \frac{1}{2}}}}} = \dfrac{1}{{{x^{\frac{3}{2}}}}} = {x^{ - \frac{3}{2}}}\\ \Rightarrow y' = - \dfrac{3}{2}{x^{ - \frac{3}{2} - 1}} = - \dfrac{3}{2}{x^{ - \frac{5}{2}}} = - \dfrac{3}{2}\dfrac{1}{{{x^{\frac{5}{2}}}}} = - \dfrac{3}{2}\dfrac{1}{{{x^2}\sqrt x }}\end{array}\)
Câu 28 :
Cho tứ diện \(OABC\) có \(OA,{\rm{ }}OB,{\rm{ }}OC\) đôi một vuông góc với nhau. Gọi \(H\) là hình chiếu của \(O\) trên mặt phẳng \(\left( {ABC} \right)\). Mệnh đề nào sau đây là sai?
Đáp án : D Phương pháp giải :
Xét tính đúng sai của từng đáp án, sử dụng lý thuyết đường thẳng vuông góc với mặt phẳng thì nó vuông góc với mọi đường thẳng thuộc mặt phẳng và ngược lại. Lời giải chi tiết :
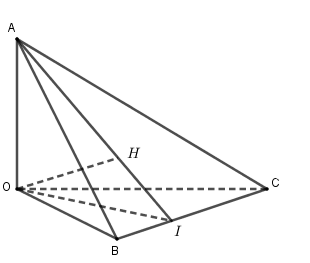 +) \(\left\{ \begin{array}{l}OA \bot OB\\OA \bot OC\end{array} \right. \Rightarrow OA \bot \left( {OBC} \right) \Rightarrow OA \bot BC.\) Do đó A đúng. +) Do \(OH \bot \left( {ABC} \right)\) nên \(OH \bot AB\) nên B đúng. Gọi \(I = AH \cap BC.\) Theo giả thiết ta có $OH \bot \left( {ABC} \right) \Rightarrow OH \bot BC.$ Suy ra \(BC \bot \left( {AOI} \right)\) \( \Rightarrow BC \bot OI,BC \bot AI\) Gọi \(J = BH \cap AC.\) Chứng minh tương tự ta có \(AC \bot BJ\). Suy ra $H$ là trực tâm \(\Delta ABC.\) Do đó C đúng. Vậy D là đáp án sai vì \(AO \bot \left( {OBC} \right)\) và \(AO \ne AH\).
Câu 29 :
Cho dãy số $({u_n})$ với ${u_n} = \dfrac{1}{{1.3}} + \dfrac{1}{{3.5}} + ... + \dfrac{1}{{\left( {2n - 1} \right).\left( {2n + 1} \right)}}$ Khi đó $\lim {u_n}$ bằng?
Đáp án : A Phương pháp giải :
- Rút gọn biểu thức, rồi tính giới hạn. Lời giải chi tiết :
$\begin{array}{l}{u_n} = \frac{1}{{1.3}} + \frac{1}{{3.5}}+ ... + \frac{1}{{\left( {2n - 1} \right).\left( {2n + 1} \right)}}\\ = \frac{1}{2}. \left( {1 - \frac{1}{3} + \frac{1}{3} - \frac{1}{5}+ ... + \frac{1}{{2n - 1}} - \frac{1}{{2n + 1}}} \right) \\ = \frac{1}{2}.\left( {1 - \frac{1}{{2n + 1}}} \right)\\ \Rightarrow \lim {u_n} = \lim \frac{1}{2}\left( {1 - \frac{1}{{2n + 1}}} \right) = \frac{1}{2}.\end{array}$
Câu 30 :
Tính đạo hàm của hàm số sau: \(f\left( x \right) = \left\{ \begin{array}{l}{x^2} - 3x + 1\,\,\,\,khi\,\,x > 1\\2x + 2\,\,\,\,\,\,\,\,\,\,\,\,\,khi\,\,x \le 1\end{array} \right.\) ta được:
Đáp án : B Phương pháp giải :
+) Tính đạo hàm của hàm số khi \(x > 1\) +) Tính đạo hàm của hàm số khi \(x < 1\) +) Sử dụng định nghĩa đạo hàm, xét sự tồn tại của đạo hàm của hàm số tại $x = 1.$ Lời giải chi tiết :
Với \(x > 1\) ta có: \(f\left( x \right) = {x^2} - 3x + 1 \Rightarrow f'\left( x \right) = 2x - 3\) Với \(x < 1\) ta có : \(f\left( x \right) = 2x + 2 \Leftrightarrow f'\left( x \right) = 2\) Với $x = 1$ ta có : \(\mathop {\lim }\limits_{x \to {1^ + }} f\left( x \right) = \mathop {\lim }\limits_{x \to {1^ + }} \left( {{x^2} - 3x + 1} \right) = - 1 \ne f\left( 1 \right) = 4 \) \(\Rightarrow \) Hàm số không liên tục tại $x = 1,$ do đó không có đạo hàm tại $x = 1.$ Vậy \(f'\left( x \right) = \left\{ \begin{array}{l}2x - 3\,\,\,khi\,\,x > 1\\2\,\,\,\,\,\,\,\,\,\,\,\,\,khi\,\,x < 1\end{array} \right.\)
Câu 31 :
Tính $\mathop {\lim }\limits_{x \to - \infty } \left( {\sqrt {{x^2} + 1} + x - 1} \right)$ bằng?
Đáp án : A Phương pháp giải :
- Nhân liên hợp để khử dạng $\infty - \infty $ - Chia cả tử và mẫu cho lũy thừa của $x$ bậc cao nhất. - Thay giới hạn $\mathop {\lim }\limits_{x \to \infty } \dfrac{C}{{{x^n}}} = 0,\,\,\,n \in {\mathbb{N}^*}$. Lời giải chi tiết :
$\begin{array}{l}\mathop {\lim }\limits_{x \to - \infty } \left( {\sqrt {{x^2} + 1} + x - 1} \right) \\ = \mathop {\lim }\limits_{x \to - \infty } \dfrac{{\left( {\sqrt {{x^2} + 1} + x - 1} \right)\left( {\sqrt {{x^2} + 1} - x + 1} \right)}}{{\sqrt {{x^2} + 1} - x + 1}} \\= \mathop {\lim }\limits_{x \to - \infty } \dfrac{{{x^2} + 1 - {{(x - 1)}^2}}}{{\sqrt {{x^2} + 1} - x + 1}}\\=\mathop {\lim }\limits_{x \to - \infty } \dfrac{{{x^2} + 1 - {x^2} + 2x - 1}}{{\sqrt {{x^2} + 1} - x + 1}} \\= \mathop {\lim }\limits_{x \to - \infty } \dfrac{{2x}}{{\sqrt {{x^2} + 1} - x + 1}} \\= \mathop {\lim }\limits_{x \to - \infty } \dfrac{{\dfrac{{2x}}{x}}}{{\dfrac{{\sqrt {{x^2} + 1} }}{x} - \dfrac{x}{x} + \dfrac{1}{x}}} \\= \mathop {\lim }\limits_{x \to - \infty } \dfrac{2}{{ - \sqrt {1 + \dfrac{1}{{{x^2}}}} - 1 + \dfrac{1}{x}}}\\ = \dfrac{2}{{ - 1 - 1 + 0}} = - 1\end{array}$
Câu 32 :
Tính$\mathop {\lim }\limits_{x \to - \infty } (x - 1)\sqrt {\dfrac{{{x^2}}}{{2{x^4} + {x^2} + 1}}} $ bằng?
Đáp án : A Phương pháp giải :
- Đưa $x - 1$ vào trong căn: $x - 1 = - \sqrt {{{(x - 1)}^2}} \,\,\,\,khi\,\,x \to - \infty $ - Chia cả tử và mẫu cho lũy thừa của $x$ bậc cao nhất. - Thay giới hạn $\mathop {\lim }\limits_{x \to \infty } \dfrac{C}{{{x^n}}} = 0,\,\,\,n \in {\mathbb{N}^*}$. Lời giải chi tiết :
$\begin{array}{l}\mathop {\lim }\limits_{x \to - \infty } (x - 1)\sqrt {\dfrac{{{x^2}}}{{2{x^4} + {x^2} + 1}}} \\= \mathop {\lim }\limits_{x \to - \infty } \left[ { - \sqrt {\dfrac{{{x^2}{{(x - 1)}^2}}}{{2{x^4} + {x^2} + 1}}} } \right] \\= \mathop {\lim }\limits_{x \to - \infty } \left[ { - \sqrt {\dfrac{{{x^2}({x^2} - 2x + 1)}}{{2{x^4} + {x^2} + 1}}} } \right]\\ = \mathop {\lim }\limits_{x \to - \infty } \left[ { - \sqrt {\dfrac{{{x^4} - 2{x^3} + {x^2}}}{{2{x^4} + {x^2} + 1}}} } \right]\\ = \mathop {\lim }\limits_{x \to - \infty } \left[ { - \sqrt {\dfrac{{1 - \dfrac{2}{x} + \dfrac{1}{{{x^2}}}}}{{2 + \dfrac{1}{{{x^2}}} + \dfrac{1}{{{x^4}}}}}} } \right] = - \dfrac{{\sqrt 2 }}{2}\end{array}$
Câu 33 :
Cho hàm số \(f\left( x \right)\) xác định trên $[a; b].$ Trong các khẳng định sau, khẳng định nào đúng?
Đáp án : D Phương pháp giải :
Nhận xét từng đáp án, sử dụng định lí: Nếu hàm số \(y = f\left( x \right)\) liên tục trên \(\left( {a;b} \right)\) và \(f\left( a \right).f\left( b \right) < 0\) thì tồn tại ít nhất một số \({x_0} \in \left( {a;b} \right)\) sao cho \(f\left( {{x_0}} \right) = 0\). Lời giải chi tiết :
Đáp án A sai. Chẳng hạn xét hàm số \(f\left( x \right) = {x^2} - 5.\) Hàm số này xác định trên \(\left[ { - 3;3} \right]\) và liên tục trên đoạn đó, đồng thời \(f\left( { - 3} \right).f\left( 3 \right) = 16 > 0\) nhưng phương trình \(f\left( x \right) = {x^2} - 5 = 0\) có nghiệm $x = \pm \sqrt 5 \in \left( { - 3;3} \right)$ Đáp án B sai vì thiếu điều kiện \(f\left( x \right)\) liên tục trên \(\left( {a;b} \right)\). Đáp án C sai. Ví dụ xét hàm số \(f\left( x \right) = \left\{ \begin{array}{l}x + 1\,\,\,khi\,\,x < 0\\x + 2\,\,khi\,\,x \ge 0\end{array} \right.\). Hàm số này xác định trên \(\left[ { - 3;3} \right]\), có nghiệm \(x = - 1\) thuộc khoảng \(\left( { - 3;3} \right)\) nhưng gián đoạn tại điểm \(x = 0 \in \left( { - 3;3} \right)\) nên không liên tục trên khoảng \(\left( { - 3;3} \right)\) . Đáp án D đúng. Thật vậy: + Vì hàm số \(y = f\left( x \right)\) liên tục tăng trên đoạn \(\left[ {a;b} \right]\) nên \(f\left( a \right) < f\left( x \right) < f\left( b \right)\,\,\forall x \in \left( {a;b} \right)\) TH1: \(\left\{ \begin{array}{l}f\left( a \right) > 0\\f\left( b \right) > 0\\f\left( a \right) < f\left( x \right) < f\left( b \right)\end{array} \right. \Rightarrow f\left( x \right) > 0\) TH2: \(\left\{ \begin{array}{l}f\left( a \right) < 0\\f\left( b \right) < 0\\f\left( a \right) < f\left( x \right) < f\left( b \right)\end{array} \right. \Rightarrow f\left( x \right) < 0\) Vậy không có giá trị nào của $x$ để \(f\left( x \right) = 0\), hay phương trình \(f\left( x \right) = 0\) không thể có nghiệm trong \(\left( {a;b} \right)\).
Câu 34 :
Cho hàm số \(f\left( x \right) = \left\{ \begin{array}{l}\dfrac{{\sqrt {{{\left( {x - 3} \right)}^2}} }}{{x - 3}}\,\,khi\,\,x \ne 3\\m\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,khi\,x = 3\end{array} \right.\). Tìm tất cả các giá trị của tham số thực $m$ để hàm số liên tục tại $x = 3.$
Đáp án : A Phương pháp giải :
Xét tính liên tục của hàm số tại $x = 3.$ Để hàm số liên tục tại $x = 3$ thì \(\mathop {\lim }\limits_{x \to 3} f\left( x \right) = f\left( 3 \right)\) Lời giải chi tiết :
Hàm số đã cho xác định trên R. Ta có \(\begin{array}{l}\mathop {\lim }\limits_{x \to {3^ - }} f\left( x \right) = \mathop {\lim }\limits_{x \to {3^ - }} \dfrac{{\sqrt {{{\left( {x - 3} \right)}^2}} }}{{x - 3}} = \mathop {\lim }\limits_{x \to {3^ - }} \dfrac{{\left| {x - 3} \right|}}{{x - 3}} = \mathop {\lim }\limits_{x \to {3^ - }} \dfrac{{ - \left( {x - 3} \right)}}{{x - 3}} = \mathop {\lim }\limits_{x \to {3^ - }} \left( { - 1} \right) = - 1\\\mathop {\lim }\limits_{x \to {3^ + }} f\left( x \right) = \mathop {\lim }\limits_{x \to {3^ + }} \dfrac{{\sqrt {{{\left( {x - 3} \right)}^2}} }}{{x - 3}} = \mathop {\lim }\limits_{x \to {3^ + }} \dfrac{{\left| {x - 3} \right|}}{{x - 3}} = \mathop {\lim }\limits_{x \to {3^ + }} \dfrac{{x - 3}}{{x - 3}} = \mathop {\lim }\limits_{x \to {3^ + }} \left( 1 \right) = 1\end{array}\) Vậy $\mathop {\lim }\limits_{x \to {3^ + }} f\left( x \right) \ne \mathop {\lim }\limits_{x \to {3^ - }} f\left( x \right) \Rightarrow $ Không tồn tại $\mathop {\lim }\limits_{x \to 3} f\left( x \right)$. Vậy không có giá trị nào của $m$ để hàm số liên tục tại $x = 3.$
Câu 35 :
Cho hàm số \(f\left( x \right) = {x^3} - 3{x^2} + 1\). Đạo hàm của hàm số f(x) âm khi và chỉ khi
Đáp án : A Phương pháp giải :
Tính \(f'\left( x \right)\) sau đó giải bất phương trình \(f'\left( x \right) < 0\) Lời giải chi tiết :
Có: \(f'\left( x \right) = 3{x^2} - 3.2x = 3{x^2} - 6x\) \(f'\left( x \right) < 0 \Leftrightarrow 3{x^2} - 6x < 0 \Leftrightarrow 0 < x < 2\)
Câu 36 :
Cho hàm số \(y = \dfrac{{x - 3}}{{x + 4}}\) có đạo hàm là $y'$ và $y''$. Mệnh đề nào sau đây đúng?
Đáp án : B Phương pháp giải :
Tính \(y',y''\) và kiểm tra tính đúng sai của từng đáp án. Lời giải chi tiết :
$\begin{array}{l}
Câu 37 :
Số tiếp tuyến đi qua điểm \(A\left( {1; - 6} \right)\) của đồ thị hàm số \(y = {x^3} - 3x + 1\) là:
Đáp án : D Phương pháp giải :
Viết phương trình tiếp tuyến của đồ thị hàm số tại điểm có hoành độ \({x_0}\,\,\left( d \right)\) Cho \(A \in \left( d \right)\), tìm \({x_0}\), có bao nhiêu nghiệm \({x_0}\) thì có bấy nhiêu tiếp tuyến của đồ thị hàm số đi qua $A.$ Lời giải chi tiết :
\(y' = 3{x^2} - 3\) \( \Rightarrow \) Phương trình tiếp tuyến của đồ thị hàm số tại điểm \(\left( {{x_0};{y_0}} \right) \in (C)\) là: \(y = \left( {3x_0^2 - 3} \right)\left( {x - {x_0}} \right) + x_0^3 - 3{x_0} + 1\,\,\left( d \right)\) $\begin{array}{l}A \in d \Rightarrow - 6 = \left( {3x_0^2 - 3} \right)\left( {1 - {x_0}} \right) + x_0^3 - 3{x_0} + 1\,\,\left( d \right)\\ \Leftrightarrow - 6 = 3x_0^2 - 3x_0^3 - 3 + 3{x_0} + x_0^3 - 3{x_0} + 1\\ \Leftrightarrow - 2x_0^3 + 3x_0^2 + 4 = 0 \Leftrightarrow {x_0} = 2\end{array}$ Vậy số tiếp tuyến đi qua điểm \(A\left( {1; - 6} \right)\) của đồ thị hàm số \(y = {x^3} - 3x + 1\) là $1$.
Câu 38 :
Số tiếp tuyến của đồ thị hàm số \(y = \dfrac{1}{3}{x^3} - 2{x^2} + 3x + 1\) song song với đường thẳng \(y = 8x + 2\) là:
Đáp án : B Phương pháp giải :
Bước 1: Viết phương trình tiếp tuyến phụ thuộc vào $x_0$ Phương trình tiếp tuyến của \(\left( C \right)\) tại điểm \(M\left( {{x_o};{y_0}} \right)\) là: \(y = f'\left( {{x_0}} \right)\left( {x - {x_0}} \right) + {y_0}\,\,\left( d \right)\) Bước 2: Sử dụng tính chất \(\left( d \right)//\left( {y = 8x + 2} \right) \Leftrightarrow f'\left( {{x_0}} \right) = 8\) Lời giải chi tiết :
Bước 1: \(y' = {x^2} - 4x + 3\) \( \Rightarrow \) Phương trình tiếp tuyến của đồ thị hàm số tại điểm có hoành độ \({x_0}\) là: \(y = \left( {x_0^2 - 4{x_0} + 3} \right)\left( {x - {x_0}} \right) + \dfrac{1}{3}x_0^3 - 2x_0^2 + 3{x_0} + 1\left( d \right)\) Bước 2: \(\left( d \right)//\left( {y = 8x + 2} \right) \Leftrightarrow f'\left( {{x_0}} \right) = 8 \Leftrightarrow x_0^2 - 4{x_0} + 3 = 8\) \( \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{{x_0} = 5}\\{{x_0} = {\rm{\;}} - 1}\end{array}} \right. \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{\left( d \right):{\mkern 1mu} {\mkern 1mu} y = 8\left( {x - 5} \right) + \dfrac{{23}}{3} = 8x - \dfrac{{97}}{3}}\\{\left( d \right):{\mkern 1mu} {\mkern 1mu} y = 8\left( {x + 1} \right) - \dfrac{{13}}{3} = 8x + \dfrac{{11}}{3}}\end{array}} \right.\) Vậy có hai tiếp tuyến cần tìm là $2$.
Câu 39 :
Cho hình chóp $S.ABCD$ có đáy là hình vuông $ABCD$ cạnh bằng $a$ và các cạnh bên đều bằng $a$. Gọi $M$ và $N$ lần lượt là trung điểm của $AD$ và $SD$. Số đo của góc $\left( {MN,SC} \right)$ bằng:
Đáp án : C Phương pháp giải :
- Chứng minh \(SA \bot SC\) bằng cách sử dụng định lý Pi-ta-go. - Sử dụng tính chất \(\left\{ \begin{array}{l}a \bot b\\b//c\end{array} \right. \Rightarrow a \bot c\) Lời giải chi tiết :
Ta có: $AC = a\sqrt 2 $ $ \Rightarrow A{C^2} = 2{a^2} = S{A^2} + S{C^2}$ $ \Rightarrow \Delta SAC$ vuông tại $S$. Khi đó: $\overrightarrow {NM} .\overrightarrow {SC} = \dfrac{1}{2}\overrightarrow {SA} .\overrightarrow {SC} = 0$ $ \Leftrightarrow \left( {\overrightarrow {NM} ,\overrightarrow {SC} } \right) = 90^\circ $ $ \Rightarrow \left( {MN,SC} \right) = 90^\circ $
Câu 40 :
Cho hình chóp $S.ABC$ có \(SA \bot (ABC)\) và tam giác $ABC$ không vuông, gọi $H,{\rm{ }}K$ lần lượt là trực tâm các tam giác$ABC$ và $SBC$. Các đường thẳng $AH,{\rm{ }}SK,{\rm{ }}BC$ thỏa mãn:
Đáp án : A Phương pháp giải :
Sử dụng tính chất \(\left\{ \begin{array}{l}a \bot \left( P \right)\\b \subset \left( P \right)\end{array} \right. \Rightarrow a \bot b\) Lời giải chi tiết :
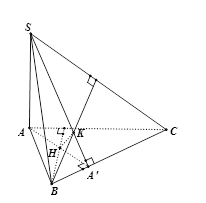 Gọi $AA'$ là đường cao của tam giác $ABC$ \( \Rightarrow AA' \bot BC\) mà \(BC \bot SA\) nên \(BC \bot SA' \Rightarrow A' \in SK\) (vì \(K\) là trực tâm của tam giác)
Câu 41 :
Cho hình chóp $S.ABC$ thỏa mãn $SA{\rm{ }} = {\rm{ }}SB{\rm{ }} = {\rm{ }}SC$. Tam giác $ABC$ vuông tại $A$. Gọi $H$ là hình chiếu vuông góc của $S$ lên $mp\left( {ABC} \right)$. Chọn khẳng định sai trong các khẳng định sau?
Đáp án : A Phương pháp giải :
Sử dụng tính chất đường thẳng vuông góc mặt phẳng và xác định giao tuyến của các mặt phẳng. Lời giải chi tiết :
Do SH\(\bot\) (ABC) nên \(SH\bot HA, SH\bot HB, SH\bot HC\). Xét các tam giác vuông SHA, SHB, SHC có: SA=SB=SC SH chung Do đó \(\Delta SAH=\Delta SBH=\Delta SCH\) Suy ra HA=HB=HC hay H là tâm đường tròn ngoại tiếp tam giác ABC. Mà tam giác ABC vuông tại A nên tâm đường tròn ngoại tiếp tam giác là trung điểm BC hay H là trung điểm của BC. Do đó $\left( SBH \right) \equiv \left( SCH \right)$ nên A sai. Lại có $\left( SAH \right)\cap ~\left( SBH \right)\text{ }=\text{ }SH$ và $\left( {SAH} \right) \cap \left( {SCH} \right){\rm{ }} = {\rm{ }}SH$ nên B và D đều đúng. Vì \(SH \bot \left( {ABC} \right) \Rightarrow SH \bot AB\) nên C đúng.
Câu 42 :
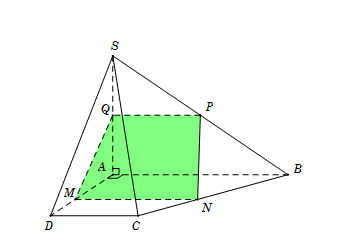
Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình chữ nhật tâm $O$ với $AB = a,$ $AD = 2a.$ Cạnh bên $SA = a$ và vuông góc với đáy. Gọi $\left( \alpha \right)$ là mặt phẳng qua $SO$ và vuông góc với $\left( {SAD} \right).$ Tính diện tích $S$ của thiết diện tạo bởi $\left( \alpha \right)$ và hình chóp đã cho.
Đáp án : B Lời giải chi tiết :
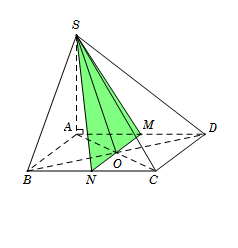 Gọi $M,{\rm{ }}N$ lần lượt là trung điểm $AD,{\rm{ }}BC$. Khi đó \( \bullet \) $MN$ đi qua $O.$ \( \bullet \) $\left\{ \begin{array}{l}MN \bot AD\\MN \bot SA\end{array} \right. \Rightarrow MN \bot \left( {SAD} \right).$ Từ đó suy ra $\left( \alpha \right) \equiv \left( {SMN} \right)$ và thiết diện cần tìm là tam giác $SMN$. Tam giác $SMN$ vuông tại $M$ nên ${S_{\Delta \,SMN}} = \dfrac{1}{2}SM.MN = \dfrac{1}{2}\sqrt {S{A^2} + {{\left( {\dfrac{{AD}}{2}} \right)}^2}} .AB = \dfrac{{{a^2}\sqrt 2 }}{2}.$
Câu 43 :
Trong mặt phẳng $\left( P \right)$ cho nửa đường tròn đường kính $AB = 2R$ và điểm $C$ thuộc nửa đường tròn đó sao cho $AC = R$. Trên đường thẳng vuông góc với $\left( P \right)$ tại $A$ lấy điểm $S$ sao cho góc giữa hai mặt phẳng $\left( {SAB} \right)$ và $\left( {SBC} \right)$ bằng ${60^0}$. Gọi $H,\,\,K$ lần lượt là hình chiếu của $A$ lên $SB,\,\,SC$. Độ dài cạnh $SA$ tính theo $R$ là
Đáp án : A Phương pháp giải :
Sử dụng phương pháp xác định góc giữa hai mặt phẳng và áp dụng các hệ thức lượng trong tam giác vuông Lời giải chi tiết :
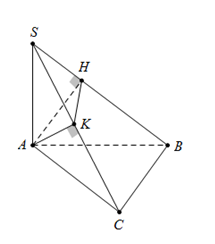 Ta có $\left\{ \begin{array}{l}BC \bot AC\\BC \bot SA\end{array} \right. \Rightarrow BC \bot \left( {SAC} \right) \Rightarrow BC \bot AK$. Do đó $AK \bot \left( {SBC} \right) \Rightarrow AK \bot KH$. \(\begin{array}{l}\left\{ \begin{array}{l}AH \bot SB\\AK \bot SB\end{array} \right. \Rightarrow SB \bot \left( {AHK} \right) \Rightarrow SB \bot HK\\\left\{ \begin{array}{l}\left( {SAB} \right) \cap \left( {SBC} \right) = SB\\\left( {SAB} \right) \supset AH \bot SB\\\left( {SAC} \right) \supset HK \bot SB\end{array} \right.\Rightarrow \widehat {\left( {\left( {SAB} \right);\left( {SBC} \right)} \right)} = \widehat {\left( {AH;HK} \right)} = \widehat {AHK} = {60^0}\end{array}\) Xét tam giác AHK vuông tại K có: $AK = AH.\sin {60^0} \Leftrightarrow A{K^2} = \dfrac{3}{4}A{H^2} \Leftrightarrow \dfrac{3}{4}\dfrac{1}{{A{K^2}}} = \dfrac{1}{{A{H^2}}}$. Đặt SA = a, áp dụng hệ thức lượng, ta được
Suy ra $\dfrac{3}{4}\left( {\dfrac{1}{{{a^2}}} + \dfrac{1}{{{R^2}}}} \right) = \dfrac{1}{{{a^2}}} + \dfrac{1}{{4{R^2}}} \Leftrightarrow \dfrac{1}{4}\dfrac{1}{{{a^2}}} = \dfrac{1}{2}\dfrac{1}{{{R^2}}} \Leftrightarrow {a^2} = \dfrac{{{R^2}}}{2} \Leftrightarrow a = \dfrac{R}{{\sqrt 2 }}$.
Câu 44 :
Cho tứ diện $SABC$ trong đó$SA$, $SB$, $SC$ vuông góc với nhau từng đôi một và$SA = 3a$, $SB = a$,$SC = 2a$. Khoảng cách từ $A$ đến đường thẳng $BC$ bằng:
Đáp án : B Phương pháp giải :
- Dựng hình chiếu vuông góc của \(A\) trên \(BC\). - Tính khoảng cách dựng được dựa vào các tính chất trong tam giác vuông. Lời giải chi tiết :
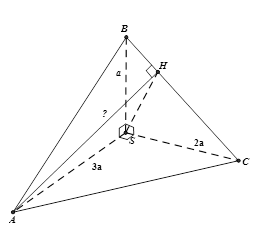 + Dựng $AH \bot BC$ $ \Rightarrow d\left( {A,BC} \right) = AH$. + $\left\{ \begin{array}{l}AS \bot \left( {SBC} \right) \supset BC \Rightarrow AS \bot BC\\AH \bot BC\end{array} \right.$, $AH$cắt $AS$ cùng nằm trong $\left( {SAH} \right)$. $ \Rightarrow BC \bot \left( {SAH} \right) \supset SH \Rightarrow BC \bot SH$. Xét trong $\Delta SBC$ vuông tại $S$ có $SH$ là đường cao ta có: $\dfrac{1}{{S{H^2}}} = \dfrac{1}{{S{B^2}}} + \dfrac{1}{{S{C^2}}} = \dfrac{1}{{{a^2}}} + \dfrac{1}{{4{a^2}}} = \dfrac{5}{{4{a^2}}}$ $ \Rightarrow S{H^2} = \dfrac{{4{a^2}}}{5}$ $ \Rightarrow SH = \dfrac{{2a\sqrt 5 }}{5}$. + Ta dễ chứng minh được $AS \bot \left( {SBC} \right) \supset SH \Rightarrow AS \bot SH$ $ \Rightarrow \Delta ASH$ vuông tại $S$. Áp dụng định lý Pi-ta-go cho $\Delta ASH$ vuông tại $S$ta có: $A{H^2} = S{A^2} + S{H^2} = 9{a^2} + \dfrac{{4{a^2}}}{5} = \dfrac{{49{a^2}}}{5}$ $ \Rightarrow AH = \dfrac{{7a\sqrt 5 }}{5}$.
Câu 45 :
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình chữ nhật với \(AB = a,{\rm{ }}AD = 2a\). Cạnh bên \(SA\) vuông góc với đáy, góc giữa \(SD\) với đáy bằng \({60^0}.\) Tính khoảng cách \(d\) từ điểm \(C\) đến mặt phẳng \(\left( {SBD} \right)\) theo \(a\).
Đáp án : A Phương pháp giải :
Sử dụng phương pháp kẻ chân đường cao từ điểm đến mặt phẳng (lý thuyết đường thẳng vuông góc với mặt phẳng) để xác định khoảng cách từ một điểm đến mặt phẳng Lời giải chi tiết :
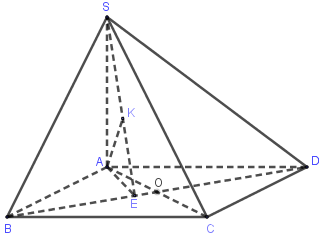 Xác định \({60^0} = \widehat {\left( {SD,\left( {ABCD} \right)} \right)} = \widehat {\left( {SD,AD} \right)} = \widehat {SDA}\) và \(SA = AD.\tan \widehat {SDA} = 2a\sqrt 3 \). Gọi $O$ là tâm hình chữ nhật $ABCD$ ta có $\begin{array}{l}CA \cap \left( {SBD} \right) = O \Rightarrow \dfrac{{d\left( {C;\left( {SBD} \right)} \right)}}{{d\left( {A;\left( {SBD} \right)} \right)}} = \dfrac{{CO}}{{AO}} = 1\\ \Rightarrow d\left( {C;\left( {SBD} \right)} \right) = d\left( {A;\left( {SBD} \right)} \right)\end{array}$. Trong $(ABCD)$ kẻ \(AE \bot BD\) và trong $(SAE)$ kẻ \(AK \bot SE\,\,\,\left( 1 \right)\). Ta có: \(\left\{ \begin{array}{l}BD \bot AE\\BD \bot SA\end{array} \right. \Rightarrow BD \bot \left( {SAE} \right) \Rightarrow BD \bot AK\,\,\,\left( 2 \right)\) Từ (1) và (2) \( \Rightarrow AK \bot \left( {SBD} \right) \Rightarrow d\left( {A;\left( {SBD} \right)} \right) = AK\). Tam giác vuông \(BAD\), có \(AE = \dfrac{{AB.AD}}{{\sqrt {A{B^2} + A{D^2}} }} = \dfrac{{2a}}{{\sqrt 5 }}\). Tam giác vuông \(SAE\), có \(AK = \dfrac{{SA.AE}}{{\sqrt {S{A^2} + A{E^2}} }} = \dfrac{{a\sqrt 3 }}{2}\). Vậy $d\left( {C;\left( {SBD} \right)} \right) = AK = \dfrac{{a\sqrt 3 }}{2}.$
Câu 46 :
Cho hình chóp $S.ABC $ có đáy $ABC$ là tam giác vuông tại $B, AB = 3a, BC = 4a.$ Cạnh bên $SA$ vuông góc với đáy. Góc tạo bởi giữa $SC$ và đáy bằng ${60^0}$. Gọi $M$ là trung điểm của $AC,$ tính khoảng cách $d$ giữa hai đường thẳng $AB$ và $SM.$
Đáp án : D Phương pháp giải :
Dựa vào phương pháp xác định mặt phẳng chứa đường thẳng này và song song với đường thẳng kia đưa về tính khoảng cách từ một điểm đến một mặt phẳng Lời giải chi tiết :
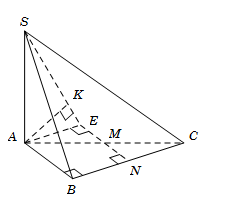 Ta có: \(AC = \sqrt {A{B^2} + B{C^2}} = 5a\) Xác định \({60^0} = \widehat {\left( {SC,\left( {ABC} \right)} \right)} = \widehat {\left( {SC,AC} \right)} = \widehat {SCA}\) và \(SA = AC.\tan \widehat {SCA} = 5a\sqrt 3 .\) Gọi \(N\) là trung điểm \(BC\), suy ra \(MN\parallel AB\). Lấy điểm \(E\) đối xứng với \(N\) qua \(M\), suy ra \(ABNE\) là hình chữ nhật. Do đó $d\left( {AB;SM} \right) = d\left( {AB;\left( {SME} \right)} \right) = d\left( {A;\left( {SME} \right)} \right).$ Kẻ \(AK \bot SE\). Vì \(ME \bot AE,ME \bot SA\) nên \(ME \bot \left( {SAE} \right) \Rightarrow ME \bot AK\) Mà \(AK \bot SE\) nên \(AK \bot \left( {SME} \right)\) Khi đó \(d\left( {A;\left( {SME} \right)} \right) = AK = \dfrac{{SA.AE}}{{\sqrt {S{A^2} + A{E^2}} }} = \dfrac{{10a\sqrt 3 }}{{\sqrt {79} }}.\)
Câu 47 :
Cho hình hộp chữ nhật $ABCD.A’B’C’D’$ có đáy $ABCD$ là hình vuông cạnh \(a\sqrt 2 \), $AA’ = 2a$. Tính khoảng cách $d$ giữa hai đường thẳng $BD$ và $CD’$.
Đáp án : C Phương pháp giải :
Dựa vào phương pháp xác định mặt phẳng chứa đường thẳng này và song song với đường thẳng kia đưa về tính khoảng cách từ một điểm đến một mặt phẳng Lời giải chi tiết :
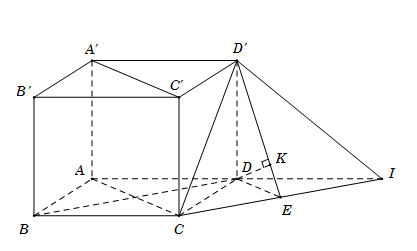 Gọi $I$ là điểm đối xứng của $A$ qua $D$, suy ra $BCID$ là hình bình hành nên $BD//CI$ Do đó \(d\left( {BD;CD'} \right) = d\left( {BD;\left( {CD'I} \right)} \right) = d\left( {D;\left( {CD'I} \right)} \right).\) Kẻ \(DE \bot CI\) tại \(E\), kẻ $DK \bot D'E\,\,\left( 1 \right)$ ta có: \(\left\{ \begin{array}{l}CI \bot DE\\CI \bot DD'\end{array} \right. \Rightarrow CI \bot \left( {DD'E} \right) \Rightarrow CI \bot DK\,\,\left( 2 \right)\) Từ (1) và (2) \( \Rightarrow DK \bot \left( {CD'I} \right) \) \(\Rightarrow d\left( {D;\left( {CD'I} \right)} \right) = DK.\) Xét tam giác $IAC$, ta có $DE // AC$ (do cùng vuông góc với $CI$) và có $D$ là trung điểm của $AI$ nên suy ra $DE$ là đường trung bình của tam giác $ACI$. Suy ra \(DE = \dfrac{1}{2}AC = \dfrac{{a\sqrt 2 }}{{\sqrt 2 }} = a.\) Tam giác vuông $D'DE$, có $DK = \dfrac{{D'D.DE}}{{\sqrt {D'{D^2} + D{E^2}} }} = \dfrac{{2a.a}}{{\sqrt {4{a^2} + {a^2}} }} = \dfrac{{2a\sqrt 5 }}{5}.$
Câu 48 :
Cho hình chóp \(S.ABDC\), với đáy \(ABCD\) là hình bình hành tâm \(O;AD,SA,AB\) đôi một vuông góc \(AD = 8,SA = 6\). \((P)\)là mặt phẳng qua trung điểm của \(AB\) và vuông góc với \(AB\). Thiết diện của \((P)\) và hình chóp có diện tích bằng?
Đáp án : D Phương pháp giải :
- Xác định thiết diện, sử dụng tính chất đường thẳng vuông góc mặt phẳng: “Nếu một đường thẳng vuông góc với mặt phẳng thì nó vuông góc với mọi đường thẳng nằm trong mặt phẳng đó”. - Chứng thiết diện là hình thang vuông và tính diện tích. Lời giải chi tiết :
Gọi \(E\) là trung điểm của \(AB\). Qua \(E\) kẻ \(EF \bot CD,EG \bot AB \Rightarrow \left( {EGF} \right) \bot AB\) và \(F,G\) là trung điểm của \(DC,SB\). Do \(\left\{ \begin{array}{l}\left( {SBC} \right) \cap \left( {ABCD} \right) = BC\\\left( {EGF} \right) \cap \left( {ABCD} \right) = FE\\FE//BC\end{array} \right. \) \(\Rightarrow \left( {SBC} \right) \cap \left( {EGF} \right) = GH//BC\) (định lý giao tuyến ba mặt phẳng) Suy ra \(H\) là trung điểm của \(SC\). Vậy thiết diện là hình thang \(GHFE\). Vì \(GE//SA\) nên \(GE \bot \left( {ABCD} \right) \Rightarrow GE \bot FE\) nên thiết diện là hình thang vuông. \({S_{EGHF}} = \dfrac{{\left( {FE + GH} \right).GE}}{2} \) \(= \dfrac{{\left( {BC + \dfrac{1}{2}BC} \right).\dfrac{1}{2}SA}}{2} \) \( = \dfrac{{\left( {8 + 4} \right)3}}{2} = 18\)
Câu 49 :
Cho \(a, b\) là các số thực khác \(0\). Tìm hệ thức liên hệ giữa \(a\) và \(b\) để hàm số sau liên tục tại \(x = 0\): \(f\left( x \right) = \left\{ \begin{array}{l}\dfrac{{\sqrt {ax + 1} \sqrt[3]{{bx + 1}} - 1}}{x}\,\,\,\,\,khi\,x \ne 0\\a + b\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,khi\,\,x = 0\end{array} \right.\)
Đáp án : C Phương pháp giải :
Xét tính liên tục của hàm số tại \(x = 0\). Để hàm số liên tục tại \(x = 0\) thì \(\mathop {\lim }\limits_{x \to 0} f\left( x \right) = f\left( 0 \right).\) Lời giải chi tiết :
Ta có: $\begin{array}{l}\mathop {\lim }\limits_{x \to 0} f\left( x \right) = \mathop {\lim }\limits_{x \to 0} \dfrac{{\sqrt {ax + 1} \sqrt[3]{{bx + 1}} - 1}}{x} \\= \mathop {\lim }\limits_{x \to 0} \dfrac{{\left( {\sqrt {ax + 1} - 1} \right)\left( {\sqrt[3]{{bx + 1}} - 1} \right) + \left( {\sqrt {ax + 1} - 1} \right) + \left( {\sqrt[3]{{bx + 1}} - 1} \right)}}{x}\\ = \mathop {\lim }\limits_{x \to 0} \dfrac{{\dfrac{{ax + 1 - 1}}{{\sqrt {ax + 1} + 1}}.\dfrac{{bx + 1 - 1}}{{{{\sqrt[3]{{bx + 1}}}^2} + \sqrt[3]{{bx + 1}} + 1}} + \dfrac{{ax + 1 - 1}}{{\sqrt {ax + 1} + 1}} + \dfrac{{bx + 1 - 1}}{{{{\sqrt[3]{{bx + 1}}}^2} + \sqrt[3]{{bx + 1}} + 1}}}}{x}\\ = \mathop {\lim }\limits_{x \to 0} \left[ {\dfrac{{abx}}{{\left( {\sqrt {ax + 1} + 1} \right)\left( {{{\sqrt[3]{{bx + 1}}}^2} + \sqrt[3]{{bx + 1}} + 1} \right)}} + \dfrac{a}{{\sqrt {ax + 1} + 1}} + \dfrac{b}{{{{\sqrt[3]{{bx + 1}}}^2} + \sqrt[3]{{bx + 1}} + 1}}} \right]\\ = 0 + \dfrac{a}{2} + \dfrac{b}{3} = \dfrac{a}{2} + \dfrac{b}{3}\end{array}$ Để hàm số liên tục tại \(x = 0 \) thì \(\mathop {\lim }\limits_{x \to 0} f\left( x \right) = f\left( 0 \right) \Leftrightarrow \dfrac{a}{2} + \dfrac{b}{3} = a + b \Leftrightarrow \dfrac{a}{2} + \dfrac{{2b}}{3} = 0 \Leftrightarrow 3a + 4b = 0\)
Câu 50 :
Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình chữ nhật, $BC = a$. Cạnh bên $SA$ vuông góc với đáy, góc $\widehat {SCA} = \widehat {BSC} = {30^0}$. Gọi $M$ là trung điểm của $CD$. Tính khoảng cách từ $D$ đến mặt phẳng $\left( {SAM} \right)$.
Đáp án : A Phương pháp giải :
Sử dụng phương pháp kẻ chân đường cao từ điểm đến mặt phẳng (lý thuyết đường thẳng vuông góc với mặt phẳng) để xác định khoảng cách từ một điểm đến mặt phẳng Lời giải chi tiết :
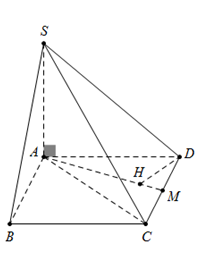 Đặt $AB = x \Rightarrow AC = \sqrt {A{B^2} + B{C^2}} = \sqrt {{x^2} + {a^2}} \Rightarrow $$SA = AC.\tan \widehat {SCA} = \sqrt {\dfrac{{{x^2} + {a^2}}}{3}} .$ Ta có : \(\left\{ \begin{array}{l}BC \bot AB\\BC \bot SA\end{array} \right. \Rightarrow BC \bot \left( {SAB} \right) \Rightarrow BC \bot SB \Rightarrow \Delta SBC\) vuông tại $B,$ có $SB = \dfrac{{BC}}{{\tan \widehat {BSC}}} = a\sqrt 3 .$ Tam giác $SAB$ vuông tại $A,$ có $S{A^2} + A{B^2} = S{B^2}$. $ \Rightarrow \dfrac{{{x^2} + {a^2}}}{3} + {x^2} = 3{a^2} \Leftrightarrow 4{x^2} = 8{a^2} \Leftrightarrow x = a\sqrt 2 .$ Kẻ $DH \bot AM$, ta có $\left\{ \begin{array}{l}SA \bot DH\\AM \bot DH\end{array} \right. \Rightarrow DH \bot \left( {SAM} \right).$ \( \Rightarrow d\left( {D;\left( {SAM} \right)} \right) = DH\) Xét $\Delta AMD$ vuông tại $D$, có $\dfrac{1}{{D{H^2}}} = \dfrac{1}{{A{D^2}}} + \dfrac{1}{{M{D^2}}} = \dfrac{3}{{{a^2}}}.$ $ \Rightarrow DH = \dfrac{a}{{\sqrt 3 }} \Rightarrow d\left( {D;\left( {SAM} \right)} \right) = \dfrac{a}{{\sqrt 3 }}.$ |