Đề thi, đề kiểm tra Toán lớp 11

Đề thi giữa kì 2 Toán 11 - Đề số 1

Làm đề thi

Đề bài

Câu 1 :

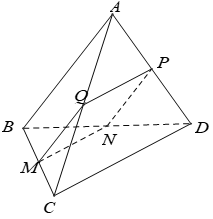
Cho tứ diện đều $ABCD$,$M$ và $N$ theo thứ tự là trung điểm của cạnh $AB$ và $CD$. Mệnh đề nào sau đây sai?

A

$\overrightarrow {AC} + \overrightarrow {BD} = \overrightarrow {AD} + \overrightarrow {BC} $
B

$\overrightarrow {MN} = \dfrac{1}{2}\left( {\overrightarrow {AD} + \overrightarrow {BC} } \right)$
C

$\overrightarrow {AC} + \overrightarrow {BD} + \overrightarrow {AD} + \overrightarrow {BC} = - 4\overrightarrow {NM} $.
D

$\overrightarrow {MC} + \overrightarrow {MD} - 4\overrightarrow {MN} = \overrightarrow 0 $.

Câu 2 :

Giới hạn $\lim \left( {\sqrt {{n^2} - n + 1} - \sqrt {{n^2} + 1} } \right)$ bằng?

A

$0.$
B

$ - \dfrac{1}{2}.$
C

$ - \dfrac{1}{{\sqrt 2 }}.$
D

$\dfrac{1}{{\sqrt 2 }}.$

Câu 3 :

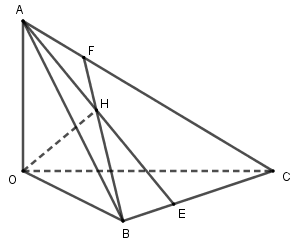
Cho tứ diện $OABC$ có $OA,OB,OC$ đôi một vuông góc với nhau. Gọi $H$ là hình chiếu của $O$ trên $mp(ABC)$. Mệnh đề nào sai trong các mệnh đề sau:

A

$H$ là trực tâm $\Delta ABC$.
B

$H$ là tâm đường tròn ngoại tiếp tam giác $ABC$.
C

$\dfrac{1}{{O{H^2}}} = \dfrac{1}{{O{A^2}}} + \dfrac{1}{{O{B^2}}} + \dfrac{1}{{O{C^2}}}$
D

$CH$ là đường cao của $\Delta ABC$.

Câu 4 :

Trong không gian cho đường thẳng $\Delta $ không nằm trong mp $\left( P \right)$, đường thẳng $\Delta $ được gọi là vuông góc với mp $\left( P \right)$ nếu:

A

vuông góc với hai đường thẳng phân biệt nằm trong mp $\left( P \right).$
B

vuông góc với đường thẳng $a$ mà $a$ song song với mp $\left( P \right)$
C

vuông góc với đường thẳng $a$ nằm trong mp $\left( P \right).$
D

vuông góc với mọi đường thẳng nằm trong mp $\left( P \right).$

Câu 5 :

Trong các dãy số sau, dãy số nào là cấp số cộng?

A

$ - 3;1;5;9;14$
B

$5;2; - 1; - 4; - 7$
C

$\dfrac{5}{3},1,\dfrac{1}{3}, - \dfrac{1}{3}, - 3$
D

$ - \dfrac{7}{2}, - \dfrac{5}{2}, - 2; - \dfrac{1}{2};\dfrac{1}{2}$

Câu 6 :

Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình vuông cạnh $a.$ Cạnh bên $SA$ vuông góc với $mp\,\,\left( {ABCD} \right).$ Gọi $\left( \alpha \right)$ là mặt phẳng qua $A$ và vuông góc với $SB.$ Mặt phẳng $\left( \alpha \right)$ cắt hình chóp theo thiết diện là hình gì ?

A

Hình thang cân
B

Hình thang vuông
C

Hình chữ nhật
D

Hình vuông

Câu 7 :

Ba số dương lập thành cấp số nhân, tích của số hạng thứ nhất và số hạng thứ ba bằng $36$. Một cấp số cộng có $n$ số hạng, công sai $d = 4$, tổng các số hạng bằng $510$. Biết số hạng đầu của cấp số cộng bằng số hạng thứ 2 của cấp số nhân. Khi đó $n$ bằng:

A

$12$
B

$13$
C

$14$
D

$15$

Câu 8 :

Cho cấp số nhân$\left( {{u_n}} \right)$, biết:${u_1} = - 2,\,{u_2} = 8$ . Lựa chọn đáp án đúng.

A

${S_5} = - 512$
B

${u_5} = 256$
C

${u_5} = - 512$
D

$q = 4$

Câu 9 :

Cho tứ diện $ABCD$ có các cạnh đều bằng $a$. Hãy chỉ ra mệnh đề đúng trong các mệnh đề sau

A

$\overrightarrow {AD} + \overrightarrow {CD} + \overrightarrow {BC} + \overrightarrow {DA} = \overrightarrow 0 $
B

$\overrightarrow {AB} .\overrightarrow {AC} = \dfrac{{{a^2}\sqrt 3 }}{2}$
C

$\overrightarrow {AC} .\overrightarrow {AD} = \overrightarrow {AC} .\overrightarrow {CD} $
D

$\overrightarrow {AB} .\overrightarrow {CD} = 0$

Câu 10 :

Cho tứ diện $ABCD$ có $AB,\,\,BC,\,\,CD$ đôi một vuông góc với nhau. Điểm nào dưới đây cách đều bốn đỉnh $A,\,\,B,\,\,C,\,\,D$ của tứ diện $ABCD$ ?

A

Trung điểm của cạnh $BD.$
B

Tâm đường tròn ngoại tiếp tam giác $ABC.$
C

Trung điểm của cạnh $AD.$
D

Trọng tâm của tam giác $ACD.$

Câu 11 :

Cho hình chóp $S.ABCD$ có $SA \bot \left( {ABCD} \right)$ và đáy $ABCD$ là hình chữ nhật. Gọi $O$ là tâm của $ABCD$ và $I$ là trung điểm của $SC$. Khẳng định nào sau đây sai ?

A

$IO \bot \left( {ABCD} \right).$
B

$BC \bot SB.$
C

$\left( {SAC} \right)$ là mặt phẳng trung trực của đoạn $BD.$
D

Tam giác $SCD$ vuông ở $D.$

Câu 12 :

Dãy số nào sau đây có giới hạn $0$?

A

${u_n} = \dfrac{n}{2}$
B

${u_n} = \dfrac{2}{n}$
C

${u_n} = n$
D

${u_n} = \sqrt n $

Câu 13 :

Cho hình chóp $S.ABC$ có đáy $ABC$ là tam giác đều cạnh $2a,\,\,\,SA \bot \left( {ABC} \right),\,\,\,SA = \dfrac{{a\sqrt 3 }}{2}.$ Gọi $\left( P \right)$ là mặt phẳng đi qua $A$ và vuông góc với $BC.$ Thiết diện của hình chóp $S.ABC$ được cắt bởi $\left( P \right)$ có diện tích bằng ?

A

$\dfrac{{3{a^2}}}{8}.$
B

$\dfrac{{3{a^2}}}{2}.$
C

$\dfrac{{3{a^2}}}{4}.$
D

$\dfrac{{2{a^2}}}{3}.$

Câu 14 :

Cho dãy số $\left( {{x_n}} \right)$ với ${x_n} = \dfrac{{an + 4}}{{n + 2}}$. Dãy số $\left( {{x_n}} \right)$ là dãy số tăng khi:

A

a = 2
B

a > 2
C

a < 2
D

a > 1

Câu 15 :

Cho cấp số nhân $\left( {{u_n}} \right)$, biết: ${u_1} = 3,{u_5} = 48$ . Lựa chọn đáp án đúng.

A

${u_3} = 12.\,\,\,\,$
B

${u_3} = - 12.$
C

${u_3} = 16.$
D

${u_3} = - 16.$

Câu 16 :

Cho hình chóp $S.ABCD$ có $SA \bot \left( {ABCD} \right)$ và $AB \bot BC$. Dựng $AH$ là đường cao của $\Delta SAB$. Khẳng định nào sau đây sai?

A

$SA \bot CD$.
B

$AH \bot BC$.
C

$AH \bot \left( {SCD} \right)$.
D

$AH \bot SC$.

Câu 17 :

Dãy số nào trong các dãy số sau không phải là cấp số nhân:

A

${u_n} = {5^n}$
B

${u_n} = {\left( {2 - \sqrt 3 } \right)^{n + 1}}$
C

${u_n} = 5n + 1$
D

${u_n} = {4^n}$

Câu 18 :

Cho cấp số cộng $\left( {{u_n}} \right)$ với $\left\{ \begin{array}{l}{u_3} + {u_5} = 5\\{u_3}.{u_5} = 6\end{array} \right..$ Tìm số hạng đầu của cấp số cộng.

A

$\left[ \begin{array}{l}{u_1} = 1\\{u_1} = 4\end{array} \right.$
B

$\left[ \begin{array}{l}{u_1} = 1\\{u_1} = - 4\end{array} \right.$
C

$\left[ \begin{array}{l}{u_1} = - 1\\{u_1} = 4\end{array} \right.$
D

$\left[ \begin{array}{l}{u_1} = - 1\\{u_1} = 1\end{array} \right.$

Câu 19 :

Cho dãy số $\left( {{a_n}} \right)$ xác định bởi ${a_n} = 2017\sin \dfrac{{n\pi }}{2} + 2018\cos \dfrac{{n\pi }}{3}$. Mệnh đề nào dưới đây là mệnh đề đúng?

A

${a_{n + 6}} = {a_n},\forall n \in {\mathbb{N}^*}$.
B

${a_{n + 9}} = {a_n},\forall n \in {\mathbb{N}^*}$.
C

${a_{n + 12}} = {a_n},\forall n \in {\mathbb{N}^*}$.
D

${a_{n + 15}} = {a_n},\forall n \in {\mathbb{N}^*}$.

Câu 20 :

Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình vuông cạnh $a.$ Cạnh bên $SA$ vuông góc với $mp\,\,\left( {ABCD} \right),\,\,SA = a\sqrt 2 .$ Gọi $\left( \alpha \right)$ là mặt phẳng qua $A$ và vuông góc với $SB.$ Mặt phẳng $\left( \alpha \right)$ cắt hình chóp theo một thiết diện có diện tích $S.$ Tính $S$ theo $a.$

A

$S = \dfrac{{5{a^2}\sqrt 6 }}{{12}}.$
B

$S = \dfrac{{5{a^2}\sqrt 6 }}{{18}}.$
C

$S = \dfrac{{5{a^2}\sqrt 6 }}{3}.$
D

$S = \dfrac{{5{a^2}\sqrt 6 }}{5}.$

Câu 21 :

Cho hình chóp $S.ABCD$, đáy $ABCD$ là hình vuông cạnh bằng $a$ và $SA \bot \left( {ABCD} \right)$. Biết $SA = \dfrac{{a\sqrt 6 }}{3}$. Tính góc giữa $SC$ và $\left( {ABCD} \right)$.

A

$30^\circ $.
B

$45^\circ $.
C

$60^\circ $.
D

$75^\circ $.

Câu 22 :

Chọn mệnh đề sai:

A

$\lim n = + \infty $
B

$\lim \sqrt n = + \infty $
C

$\lim \sqrt[3]{n} = + \infty $
D

$\lim \dfrac{1}{n} = + \infty $

Câu 23 :

Cho tứ diện đều $ABCD$ có tam giác $BCD$ đều,$AD = AC$. Giá tri của $\cos \left( {\overrightarrow {AB} ,\overrightarrow {CD} } \right)$là:

A

$\dfrac{1}{2}$
B

$0$
C

$ - \dfrac{1}{2}$.
D

$\dfrac{{\sqrt 3 }}{2}$.

Câu 24 :

Cho tứ diện $ABCD$ có $AB$ vuông góc với $CD$. Mặt phẳng $\left( P \right)$ song song với $AB$ và $CD$ lần lượt cắt $BC,{\rm{ }}DB,{\rm{ }}AD,{\rm{ }}AC$ tại $M,{\rm{ }}N,{\rm{ }}P,{\rm{ }}Q$. Tứ giác $MNPQ$ là hình gì?

A

Hình thang
B

Hình bình hành
C

Hình chữ nhật
D

Hình vuông

Câu 25 :

Cho tứ diện $OABC$ có $OA,OB,OC$ đôi một vuông góc với nhau. Gọi $H$ là hình chiếu của $O$ trên mặt phẳng $\left( {ABC} \right)$. Xét các mệnh đề sau :

I. Vì $OC \bot OA,OC \bot OB$ nên $OC \bot \left( {OAB} \right)$.

II. Do $AB \subset \left( {OAB} \right)$nên $AB \bot OC.{\rm{ }}\left( 1 \right)$

III. Có $OH \bot \left( {ABC} \right)$ và $AB \subset \left( {ABC} \right)$nên $AB \bot OH.{\rm{ }}\left( 2 \right)$

IV. Từ $\left( 1 \right)$ và $\left( 2 \right) \Rightarrow AB \bot \left( {OCH} \right)$

Số mệnh đề đúng trong các mệnh đề trên là:

A

$4$.
B

$3$.
C

$2$.
D

$1$.

Câu 26 :

Dùng quy nạp chứng minh mệnh đề chứa biến $P\left( n \right)$ đúng với mọi số tự nhiên $n \ge p$ ($p$ là một số tự nhiên). Ở bước 2 ta giả thiết mệnh đề $P\left( n \right)$ đúng với $n = k$. Khẳng định nào sau đây là đúng?

A

$k \ne p.$
B

$k \ge p.$
C

$k = p.$
D

$k < p.$

Câu 27 :

Cho hình chóp $S.ABC$ có đáy $ABC$ là tam giác đều cạnh $a$ và $SA = SB = SC = b$ ($a > b\sqrt 2 $). Gọi $G$ là trọng tâm$\Delta \,ABC$. Xét mặt phẳng $\left( P \right)$ đi qua $A$ và vuông góc với $SC$ tại điểm I nằm giữa $S$ và $C$. Diện tích thiết diện của hình chóp khi cắt bởi mặt phẳng $\left( P \right)$ là

A

$S = \dfrac{{{a^2}\sqrt {3{b^2} - 2ab} }}{{4b}}$
B

$S = \dfrac{{{a^2}\sqrt {3{b^2} - 2ab} }}{{2b}}$
C

$S = \dfrac{{{a^2}\sqrt {3{b^2} + 2ab} }}{{2b}}$
D

$S = \dfrac{{{a^2}\sqrt {3{b^2} + 2ab} }}{{4b}}$

Câu 28 :

Giá trị $\lim \dfrac{{\sin \left( {n!} \right)}}{{{n^2} + 1}}$ bằng

A

$0.$
B

$1.$
C

$ + \infty .$
D

$2.$

Câu 29 :

Cho tứ diện $ABCD$ đều. Gọi $\alpha $ là góc giữa $AB$ và $mp(BCD)$. Chọn khẳng định đúng trong các khẳng định sau?

A

$\cos \alpha = \dfrac{{\sqrt 3 }}{3}$.
B

$\cos \alpha = \dfrac{{\sqrt 3 }}{4}$.
C

$\cos \alpha = 0$.
D

$\cos \alpha = \dfrac{{\sqrt 3 }}{2}$.

Câu 30 :

Cho các số thực $x,y,z$ thỏa mãn điều kiện ba số $\dfrac{1}{{x + y}},\dfrac{1}{{y + z}},\dfrac{1}{{z + x}}$ theo thứ tự lập thành một cấp số cộng. Mệnh đề nào dưới đây là mệnh đề đúng ?

A

Ba số ${x^2},{y^2},{z^2}$ theo thứ tự lập thành cấp số cộng.
B

Ba số ${y^2},{z^2},{x^2}$ theo thứ tự lập thành cấp số cộng.
C

Ba số ${y^2},{x^2},{z^2}$ theo thứ tự lập thành cấp số cộng.
D

Ba số ${z^2},{y^2},{x^2}$ theo thứ tự lập thành cấp số cộng.

Câu 31 :

Cho hình chóp $SABC$ có $SA \bot \left( {ABC} \right).$ Gọi $H,{\rm{ }}K$ lần lượt là trực tâm các tam giác $SBC$ và$ABC$. Mệnh đề nào sai trong các mệnh đề sau?

A

$BC \bot \left( {SAH} \right).$
B

$HK \bot \left( {SBC} \right).$
C

$BC \bot \left( {SAB} \right).$
D

$SH,AK$ và $BC$ đồng quy.

Câu 32 :

Cho dãy số $\left( {{a_n}} \right)$ xác định bởi ${a_1} = 1$ và ${a_{n + 1}} = - \dfrac{3}{2}a_n^2 + \dfrac{5}{2}{a_n} + 1,\,\,\forall n \in N^*.$ Mệnh đề nào dưới đây là đúng ?

A

${a_{2018}} = {a_2}$
B

${a_{2018}} = {a_1}$
C

${a_{2018}} = {a_3}$
D

${a_{2018}} = {a_4}$

Câu 33 :

Trên một bàn cờ có nhiều ô vuông. Người ta đặt $7$ hạt dẻ vào ô vuông đầu tiên, sau đó đặt tiếp vào ô vuông thứ hai nhiều hơn ô đầu tiên là $5$ hạt dẻ, tiếp tục đặt vào ô vuông thứ ba số hạt dẻ nhiều hơn ô thứ hai là $5$ hạt dẻ,… và cứ thế tiếp tục đến ô cuối cùng. Biết rằng đặt hết số ô trên bàn cờ người ta phải sử dụng hết $25450$ hạt dẻ. Hỏi bàn cờ đó có bao nhiêu ô?

A

$98$ ô
B

$100$ ô
C

$102$ ô
D

$104$ ô

Câu 34 :

Mặt sàn tầng một của một ngôi nhà cao hơn mặt sân $0,5m$. Cầu thang đi từ tầng một lên tầng hai gồm $21$ bậc, mỗi bậc cao $18cm$. Ký hiệu ${h_n}$ là độ cao của bậc thứ $n$ so với mặt sân. Viết công thức để tìm độ cao ${h_n}$.

A

${h_n} = 0,18n + 0,32\,\,\left( m \right)$
B

${h_n} = 0,18n + 0,5\,\,\left( m \right)$
C

${h_n} = 0,5n + 0,18\,\,\left( m \right)$
D

${h_n} = 0,5n - 0,32\,\,\left( m \right)$

Câu 35 :

Chu kì bán rã của nguyên tố phóng xạ poloni $210$ là $138$ ngày (nghĩa là sau $138$ ngày khối lượng của nguyên tố đó chỉ còn một nửa). Khi đó khối lượng còn lại của $20$ gam poloni $210$ sau $7314$ ngày là:

A

$2,{22.10^{ - 15}}$
B

$2,{21.10^{ - 15}}$
C

$2,{20.10^{ - 15}}$
D

$2,{23.10^{ - 15}}$

Câu 36 :

Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình thang vuông tại $A$, đáy lớn $AD = 8$, $BC = 6$, $SA$ vuông góc với mặt phẳng $\left( {ABCD} \right)$, $SA = 6.$ Gọi $M$ là trung điểm $AB.$ Gọi $\left( P \right)$ là mặt phẳng qua $M$ và vuông góc với $AB$. Thiết diện của $\left( P \right)$ và hình chóp có diện tích bằng:

A

$10.$
B

$20.$
C

$15.$
D

$16.$

Câu 37 :

Cho hình hộp $ABCD.A'B'C'D'$ có tất cả các cạnh đều bằng nhau. Trong các mệnh đề sau, mệnh đề nào có thể sai?

A

$A'C' \bot BD$.
B

$BB' \bot BD$.
C

$A'B \bot DC'$.
D

$BC' \bot A'D$.

Câu 38 :

Cho dãy số $({u_n})$ xác định bởi $\left\{ \begin{align} & u_{1}=2 \\ & {u_{n+1}}=\dfrac{{{u}_{n}}+1}{2},(n\ge 1) \end{align} \right.$ Khi đó mệnh đề nào sau đây là đúng?

A

Dãy $({u_n})$là dãy giảm tới $1$ khi $n \to + \infty $.
B

Dãy $({u_n})$là dãy tăng tới $1$ khi $n \to + \infty $.
C

Không tồn tại giới hạn của dãy $({u_n})$.
D

Cả 3 đáp án trên đều sai

Câu 39 :

Cho các số thực a, b thỏa $\left| a \right| < 1;\;\;\left| b \right| < 1$. Tìm giới hạn $I = \lim \dfrac{{1 + a + {a^2} + ... + {a^n}}}{{1 + b + {b^2} + ... + {b^n}}}$.

A

$ + \infty $
B

$\dfrac{{1 - a}}{{1 - b}}$
C

$\dfrac{{1 - b}}{{1 - a}}$
D

$1$

Câu 40 :

Cho tứ diện đều $ABCD$,$M$ là trung điểm của cạnh $AB$ và $G$ là trọng tâm cảu tam giác $BCD$. Đặt $\overrightarrow {AB} = \overrightarrow b ,\overrightarrow {AC} = \overrightarrow c ,\overrightarrow {AD} = \overrightarrow d $. Phân tích véc tơ $\overrightarrow {MG} $ theo $\overrightarrow d ,\overrightarrow b ,\overrightarrow c $ .

A

$\overrightarrow {MG} = - \dfrac{1}{6}\overrightarrow b + \dfrac{1}{3}\overrightarrow c + \dfrac{1}{3}\overrightarrow d $ .
B

$\overrightarrow {MG} = \dfrac{1}{6}\overrightarrow b + \dfrac{1}{3}\overrightarrow c + \dfrac{1}{3}\overrightarrow d $
C

$\overrightarrow {MG} = - \dfrac{1}{6}\overrightarrow b - \dfrac{1}{3}\overrightarrow c + \dfrac{1}{3}\overrightarrow d $
D

$\overrightarrow {MG} = - \dfrac{1}{6}\overrightarrow b - \dfrac{1}{3}\overrightarrow c - \dfrac{1}{3}\overrightarrow d $.

Câu 41 :

Cho hình hộp $ABCD.A'B'C'D'$. Giả sử tam giác $AB'C$ và $A'DC'$ đều có 3 góc nhọn. Góc giữa hai đường thẳng $AC$ và $A'D$ là góc nào sau đây?

A

$\widehat {BDB'}$.
B

$\widehat {AB'C}$.
C

$\widehat {DB'B}$.
D

$\widehat {DA'C'}$.

Câu 42 :

Cho hình chóp $S.ABC$ có $SA = SB = SC$ và tam giác $ABC$ vuông tại $B$. Vẽ $SH \bot \left( {ABC} \right)$, $H \in \left( {ABC} \right)$. Khẳng định nào sau đây đúng?

A

$H$ trùng với trọng tâm tam giác $ABC$.
B

$H$ trùng với trực tâm tam giác $ABC$.
C

$H$ trùng với trung điểm của $AC$.
D

$H$ trùng với trung điểm của $BC$.

Câu 43 :

Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình vuông và $SA \bot \left( {ABCD} \right)$. Gọi $I$, $J$, $K$ lần lượt là trung điểm của $AB$, $BC$ và $SB$. Khẳng định nào sau đây sai?

A

$\left( {IJK} \right){\rm{//}}\left( {SAC} \right)$.
B

$BD \bot \left( {IJK} \right)$.
C

Góc giữa $SC$ và $BD$ có số đo $60^\circ $.
D

$BD \bot \left( {SAC} \right)$.

Câu 44 :

Cho hình thoi $ABCD$ có tâm $O,\widehat {ADC} = {60^0},AC = 2a$. Lấy điểm $S$ không thuộc $\left( {ABCD} \right)$ sao cho $SO \bot \left( {ABCD} \right)$. Gọi $\alpha $ là góc giữa đường thẳng $SB$ và mặt phẳng $\left( {ABCD} \right)$ và $\tan \alpha = \dfrac{1}{2}$. Gọi $\beta $ là góc giữa $SC$ và $\left( {ABCD} \right)$, chọn mệnh đề đúng :

A

$\sin \beta = \dfrac{1}{2}$.
B

$\cot \beta = \dfrac{{\sqrt 3 }}{2}$.
C

$\tan \beta = \dfrac{{\sqrt 3 }}{2}$.
D

$\beta = {60^0}$.

Câu 45 :

Dân số của thành phố A hiện nay là $3$ triệu người. Biết rằng tỉ lệ tăng dân số hàng năm của thành phố A là $2\% $. Dân số của thành phố A sau $3$ năm nữa sẽ là:

A

$3183624$
B

$2343625$
C

$2343626$
D

$2343627$

Câu 46 :

Trong không gian cho hai tia $Ax,By$ chéo nhau sao cho $AB$ vuông góc với cả hai tia đó. Các điểm $M,N$ lần lượt thay đổi trên $Ax,By$ sao cho độ dài đoạn $MN$ luôn bằng giá trị $c$ không đổi $(c~\le AB)$. Gọi $\varphi $ là góc giữa $Ax,By$. Giá trị lớn nhất của $AM.BN$ là:

A

$\dfrac{{{c^2} - A{B^2}}}{{2(1 - \cos \varphi {\rm{)}}}}$
B

$\dfrac{{{c^2} - A{B^2}}}{{2(1 + \cos \varphi {\rm{)}}}}$
C

$\dfrac{{{c^2} + A{B^2}}}{{2(1 - \cos \varphi {\rm{)}}}}$
D

$\dfrac{{{c^2} + A{B^2}}}{{2(1 + \cos \varphi {\rm{)}}}}$

Câu 47 :

Biết rằng tồn tại hai giá trị của tham số $m$ để phương trình sau có bốn nghiệm phân biệt lập thành một cấp số cộng: ${x^4} - 10{x^2} + 2{m^2} + 7m = 0$, tính tổng lập phương của hai giá trị đó.

A

$ - \dfrac{{343}}{8}$
B

$\dfrac{{721}}{8}$
C

$ - \dfrac{{721}}{8}$
D

$\dfrac{{343}}{8}$

Câu 48 :

Giá trị của $B = {\rm{lim}}\dfrac{{\sqrt[{\rm{n}}]{{n!}}}}{{\sqrt {{n^3} + 2n} }}$ bằng:

A

$ + \infty $
B

$ - \infty $
C

$0$
D

$1$

Câu 49 :

Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình chữ nhật với $AB = a$, $AD = a\sqrt 3 $. Cạnh bên $SA = 2a$ và vuông góc với đáy. Mặt phẳng $\left( \alpha \right)$ đi qua $A$ vuông góc với $SC$. Tính diện tích $S$ của thiết diện tạo bởi $\left( \alpha \right)$ với hình chóp đã cho.

A

${S_{AMIN}} = \dfrac{{{a^2}\sqrt 6 }}{7}.$
B

${S_{AMIN}} = \dfrac{{12{a^2}\sqrt 6 }}{{35}}.$
C

${S_{AMIN}} = \dfrac{{6{a^2}\sqrt 6 }}{{35}}.$
D

${S_{AMIN}} = \dfrac{{{a^2}\sqrt 6 }}{5}.$

Câu 50 :

Bất đẳng thức nào sau đây đúng? Với mọi số nguyên dương $n$ thì:

A

$1 + \dfrac{1}{{\sqrt 2 }} + ... + \dfrac{1}{{\sqrt n }} > 2\sqrt n $
B

$1 + \dfrac{1}{{\sqrt 2 }} + ... + \dfrac{1}{{\sqrt n }} > 3\sqrt n $
C

$1 + \dfrac{1}{{\sqrt 2 }} + ... + \dfrac{1}{{\sqrt n }} < 2\sqrt n $
D

$1 + \dfrac{1}{{\sqrt 2 }} + ... + \dfrac{1}{{\sqrt n }} > 4\sqrt 5 $

Lời giải và đáp án

Câu 1 :

Cho tứ diện đều $ABCD$,$M$ và $N$ theo thứ tự là trung điểm của cạnh $AB$ và $CD$. Mệnh đề nào sau đây sai?

A

$\overrightarrow {AC} + \overrightarrow {BD} = \overrightarrow {AD} + \overrightarrow {BC} $
B

$\overrightarrow {MN} = \dfrac{1}{2}\left( {\overrightarrow {AD} + \overrightarrow {BC} } \right)$
C

$\overrightarrow {AC} + \overrightarrow {BD} + \overrightarrow {AD} + \overrightarrow {BC} = - 4\overrightarrow {NM} $.
D

$\overrightarrow {MC} + \overrightarrow {MD} - 4\overrightarrow {MN} = \overrightarrow 0 $.

Đáp án : D

Phương pháp giải :

Xét tính đúng, sai của từng đáp án dựa vào công thức trung điểm và các công thức cộng, trừ véc tơ.

Lời giải chi tiết :

A.Đúng vì: $\overrightarrow {AC} + \overrightarrow {BD} = \left( {\overrightarrow {AD} + \overrightarrow {DC} } \right) + \left( {\overrightarrow {BC} + \overrightarrow {CD} } \right) = \overrightarrow {AD} + \overrightarrow {BC} $

B. Đúng vì: $\overrightarrow {AD} + \overrightarrow {BC} = \left( {\overrightarrow {AM} + \overrightarrow {MN} + \overrightarrow {ND} } \right) + \left( {\overrightarrow {BM} + \overrightarrow {MN} + \overrightarrow {NC} } \right)$$ = 2\overrightarrow {MN} + \left( {\overrightarrow {AM} + \overrightarrow {BM} } \right) + \left( {\overrightarrow {ND} + \overrightarrow {NC} } \right) = 2\overrightarrow {MN} $

C.Đúng vì: $\overrightarrow {AC} + \overrightarrow {BD} + \overrightarrow {AD} + \overrightarrow {BC} = 2\overrightarrow {AN} + 2\overrightarrow {BN} = 2\left( {\overrightarrow {AN} + \overrightarrow {BN} } \right) = - 2\left( {\overrightarrow {NA} + \overrightarrow {NB} } \right) = - 4\overrightarrow {NM} $

Vậy D sai.

Câu 2 :

Giới hạn $\lim \left( {\sqrt {{n^2} - n + 1} - \sqrt {{n^2} + 1} } \right)$ bằng?

A

$0.$
B

$ - \dfrac{1}{2}.$
C

$ - \dfrac{1}{{\sqrt 2 }}.$
D

$\dfrac{1}{{\sqrt 2 }}.$

Đáp án : B

Phương pháp giải :

- Nhân liên hợp,

- Chia cả tử mẫu của phân thức cho n.

Lời giải chi tiết :

$\begin{array}{l}\lim ( {\sqrt {{n^2} - n + 1} - \sqrt {{n^2} + 1} } ) \\ =\lim \frac{{( {\sqrt {{n^2} - n + 1} - \sqrt {{n^2} + 1} }) ( {\sqrt {{n^2} - n + 1} + \sqrt {{n^2} + 1} } )}}{{\sqrt {{n^2} - n + 1} + \sqrt {{n^2} + 1} }}\\ = \lim \frac{{{n^2} - n + 1 - {n^2} - 1}}{{\sqrt {{n^2} - n + 1} + \sqrt {{n^2} + 1} }} \\= \lim \frac{{ - n}}{{\sqrt {{n^2} - n + 1} + \sqrt {{n^2} + 1} }} \\= \lim \frac{{ - 1}}{{\sqrt {1 - \frac{1}{n} + \frac{1}{{{n^2}}}} + \sqrt {1 + \frac{1}{{{n^2}}}} }} \\= -\frac{{1}}{2}\end{array}$

Câu 3 :

Cho tứ diện $OABC$ có $OA,OB,OC$ đôi một vuông góc với nhau. Gọi $H$ là hình chiếu của $O$ trên $mp(ABC)$. Mệnh đề nào sai trong các mệnh đề sau:

A

$H$ là trực tâm $\Delta ABC$.
B

$H$ là tâm đường tròn ngoại tiếp tam giác $ABC$.
C

$\dfrac{1}{{O{H^2}}} = \dfrac{1}{{O{A^2}}} + \dfrac{1}{{O{B^2}}} + \dfrac{1}{{O{C^2}}}$
D

$CH$ là đường cao của $\Delta ABC$.

Đáp án : B

Phương pháp giải :

Chứng minh $H$ là trực tâm tam giác $ABC$.

Lời giải chi tiết :

Ta có $OA \bot (OBC) \Rightarrow OA \bot BC,$ mà $OH \bot BC$ $ \Rightarrow BC \bot (OAH) \Rightarrow BC \bot AH$.

Tương tự, ta có $AB \bot CH$, suy ra đáp án A, D đúng.

Ta có $\dfrac{1}{{O{H^2}}} = \dfrac{1}{{O{A^2}}} + \dfrac{1}{{O{I^2}}} $ $= \dfrac{1}{{O{A^2}}} + \dfrac{1}{{O{B^2}}} + \dfrac{1}{{O{C^2}}}$

với $I = AH \cap BC$, suy ra đáp án C đúng.

Câu 4 :

Trong không gian cho đường thẳng $\Delta $ không nằm trong mp $\left( P \right)$, đường thẳng $\Delta $ được gọi là vuông góc với mp $\left( P \right)$ nếu:

A

vuông góc với hai đường thẳng phân biệt nằm trong mp $\left( P \right).$
B

vuông góc với đường thẳng $a$ mà $a$ song song với mp $\left( P \right)$
C

vuông góc với đường thẳng $a$ nằm trong mp $\left( P \right).$
D

vuông góc với mọi đường thẳng nằm trong mp $\left( P \right).$

Đáp án : D

Lời giải chi tiết :

Đường thẳng $\Delta $ được gọi là vuông góc với mặt phẳng $\left( P \right)$ nếu $\Delta $ vuông góc với mọi đường thẳng trong mặt phẳng $\left( P \right)$.(ĐN đường thẳng vuông góc với mặt phẳng).

Câu 5 :

Trong các dãy số sau, dãy số nào là cấp số cộng?

A

$ - 3;1;5;9;14$
B

$5;2; - 1; - 4; - 7$
C

$\dfrac{5}{3},1,\dfrac{1}{3}, - \dfrac{1}{3}, - 3$
D

$ - \dfrac{7}{2}, - \dfrac{5}{2}, - 2; - \dfrac{1}{2};\dfrac{1}{2}$

Đáp án : B

Phương pháp giải :

Cấp số cộng là một dãy số mà hiệu giữa hai số hạng liên tiếp là một số không đổi.

Lời giải chi tiết :

Kiểm tra từng đáp án cho đến khi tìm được đáp án đúng.

Đáp án A: $1 - \left( { - 3} \right) = 5 - 1 = 9 - 5 = 4 \ne 14 - 9 = 5$

Đáp án B:

$2 - 5 = \left( { - 1} \right) - 2 = \left( { - 4} \right) - \left( { - 1} \right) $ $= \left( { - 7} \right) - \left( { - 4} \right) = - 3 $

Đáp án B là 1 cấp số cộng.

Câu 6 :

A

Hình thang cân
B

Hình thang vuông
C

Hình chữ nhật
D

Hình vuông

Đáp án : B

Phương pháp giải :

Sử dụng lý thuyết của đường thẳng vuông góc với mặt phẳng và bài toán tìm giao tuyến của hai mặt phẳng

Lời giải chi tiết :

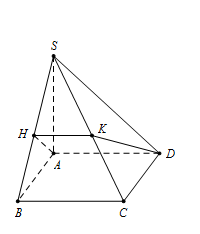Ta có $AD$ vuông góc với $SA$ và $ AB$ $ \Rightarrow AD \bot mp\,\,\left( {SAB} \right) \Rightarrow AD \bot SB.$

Vẽ đường cao $AH$ trong tam giác $SAB$

Lại có $AD$ và $AH$ qua $A$ và vuông góc với $SB.$

Vậy mặt phẳng $\left( \alpha \right)$ chính là mặt phẳng $(AHD).$

Mặt khác $AD // mp(SBC) $ mà $AD \subset mp\,\,\left( {AHD} \right)$

Vậy mặt phẳng $(SBC)$ cắt mặt phẳng $(AHD) $ theo giao tuyến $HK // AD.$

Do đó mặt cắt là hình thang $ADKH $ mà $AD \bot mp\,\,\left( {SAB} \right)$$ \Rightarrow \,AD \bot AH.$

Vậy $ADKH $ là hình thang vuông.

Câu 7 :

A

$12$
B

$13$
C

$14$
D

$15$

Đáp án : D

Phương pháp giải :

- Sử dụng tính chất của cấp số nhân để tính số hạng thứ hai của cấp số nhân và cũng là số hạng đầu tiên của cấp số cộng.

- Sử dụng công thức tổng $n$ số hạng đầu tiên của cấp số cộng để tìm $n$.

Lời giải chi tiết :

Với cấp số nhân $a,b,c > 0 \Rightarrow {b^2} = ac = 36 \Rightarrow b = 6 > 0$

Do đó, theo giả thiết cấp số cộng ta có

${u_1} = 6;d = 4;{S_n} = 510$

$\begin{array}{l}{S_n} = \dfrac{n}{2}\left( {2{u_1} + (n - 1)d} \right) \Leftrightarrow 510 = \dfrac{n}{2}\left( {12 + 4(n - 1)} \right)\\ \Leftrightarrow {n^2} + 2n - 255 = 0\\ \Rightarrow n = 15\end{array}$

(do n nguyên dương)

Câu 8 :

Cho cấp số nhân$\left( {{u_n}} \right)$, biết:${u_1} = - 2,\,{u_2} = 8$ . Lựa chọn đáp án đúng.

A

${S_5} = - 512$
B

${u_5} = 256$
C

${u_5} = - 512$
D

$q = 4$

Đáp án : C

Phương pháp giải :

- Tính công bội $q$ của cấp số nhân dựa vào công thức $q = \dfrac{{{u_{n + 1}}}}{{{u_n}}}$.

- Tính số hạng ${u_n}$ của cấp số nhân dựa vào công thức ${u_n} = {u_1}.{q^{n - 1}}$.

- Tính tổng $n$ số hạng đầu của cấp số nhân dựa vào công thức ${S_n} = \dfrac{{{u_1}\left( {1 - {q^n}} \right)}}{{1 - q}}$

Lời giải chi tiết :

Ta có: ${u_1} = - 2,{u_2} = 8 \Rightarrow q = \dfrac{{{u_2}}}{{{u_1}}} = \dfrac{8}{{ - 2}} = - 4$

Do đó ${u_5} = {u_1}.{q^4} = - 2.{\left( { - 4} \right)^4} = - 512$.

Và ${S_5} = \dfrac{{{u_1}\left( {1 - {q^5}} \right)}}{{1 - q}} = \dfrac{{ - 2\left( {1 - {{\left( { - 4} \right)}^5}} \right)}}{{\left( {1 - \left( { - 4} \right)} \right)}} = - 410$

Câu 9 :

Cho tứ diện $ABCD$ có các cạnh đều bằng $a$. Hãy chỉ ra mệnh đề đúng trong các mệnh đề sau

A

$\overrightarrow {AD} + \overrightarrow {CD} + \overrightarrow {BC} + \overrightarrow {DA} = \overrightarrow 0 $
B

$\overrightarrow {AB} .\overrightarrow {AC} = \dfrac{{{a^2}\sqrt 3 }}{2}$
C

$\overrightarrow {AC} .\overrightarrow {AD} = \overrightarrow {AC} .\overrightarrow {CD} $
D

$\overrightarrow {AB} .\overrightarrow {CD} = 0$

Đáp án : D

Phương pháp giải :

Xét tính đúng, sai của từng đáp án, sử dụng các quy tắc cộng, trừ véc tơ và nhân vô hướng hai véc tơ.

Lời giải chi tiết :

Phương án A:

$\overrightarrow {{\rm{AD}}} + \overrightarrow {CD} + \overrightarrow {BC} + \overrightarrow {DA} = \left( {\overrightarrow {AD} + \overrightarrow {DA} } \right) + \left( {\overrightarrow {BC} + \overrightarrow {CD} } \right) = \overrightarrow 0 + \overrightarrow {BD} \ne \overrightarrow 0 $ nên A sai

Phương án B:$\overrightarrow {AB} .\overrightarrow {AC} = a.a.\cos {\rm{6}}{{\rm{0}}^0}{\rm{ = }}{\dfrac{a}{2}^2}$ nên B sai

Phương án C: $\overrightarrow {AC} .\overrightarrow {AD} = \overrightarrow {AC} .\overrightarrow {CD} \Leftrightarrow \overrightarrow {AC} (\overrightarrow {AD} + \overrightarrow {DC} ) = 0 \Leftrightarrow {\overrightarrow {AC} ^2} = 0$ nên C sai.

Phương án D: Do tứ diện $ABCD$ đều nên $AB \bot CD$ hay $\overrightarrow {AB} .\overrightarrow {CD} = 0$.

Câu 10 :

Cho tứ diện $ABCD$ có $AB,\,\,BC,\,\,CD$ đôi một vuông góc với nhau. Điểm nào dưới đây cách đều bốn đỉnh $A,\,\,B,\,\,C,\,\,D$ của tứ diện $ABCD$ ?

A

Trung điểm của cạnh $BD.$
B

Tâm đường tròn ngoại tiếp tam giác $ABC.$
C

Trung điểm của cạnh $AD.$
D

Trọng tâm của tam giác $ACD.$

Đáp án : C

Phương pháp giải :

Nhận xét các tam giác $ABD,BCD$ vuông rồi suy ra điểm cách đều bốn đỉnh của tứ diện.

Lời giải chi tiết :

Ta có $\left\{ \begin{array}{l}AB \bot BC\\AB \bot CD\end{array} \right.\,\, \Rightarrow \,\,AB \bot \left( {BCD} \right)\,\, \Rightarrow $ tam giác $ABD$ vuông tại $B.$

Suy ra $IA = IB = ID = \dfrac{{AD}}{2},$ với $I$ là trung điểm của $AD.$ $\left( 1 \right)$

Lại có $\left\{ \begin{array}{l}AB \bot CD\\BC \bot CD\end{array} \right.\,\, \Rightarrow \,\,CD \bot \left( {ABC} \right)\,\, \Rightarrow \,\,$tam giác $ACD$ vuông tại $C.$

Suy ra $EA = EC = ED = \dfrac{{AD}}{2},$ với $E$ là trung điểm của $AD.$ $\left( 2 \right)$

Từ $\left( 1 \right),\left( 2 \right)$ suy ra $I \equiv E \equiv O$ nên trung điểm của cạnh $AD$ cách đều $A,\,\,B,\,\,C,\,\,D.$

Câu 11 :

A

$IO \bot \left( {ABCD} \right).$
B

$BC \bot SB.$
C

$\left( {SAC} \right)$ là mặt phẳng trung trực của đoạn $BD.$
D

Tam giác $SCD$ vuông ở $D.$

Đáp án : C

Phương pháp giải :

Sử dụng điều kiện đường thẳng vuông góc mặt phẳng và định nghĩa mặt phẳng trung trực để xét tính đúng, sai của từng đáp án.

Lời giải chi tiết :

Có $IO$ là đường trung bình tam giác $SAC$ nên $IO//SA$ nên $IO \bot \left( {ABCD} \right)$ nên A đúng.

Có $\left\{ \begin{array}{l}BC \bot AB\\BC \bot SA\end{array} \right. \Rightarrow BC \bot SB$ nên B đúng

Và $\left\{ \begin{array}{l}CD \bot AD\\CD \bot SA\end{array} \right. \Rightarrow CD \bot SD$ nên phương án D đúng.

Đáp án C sai vì nếu $\left( {SAC} \right)$ là mặt phẳng trung trực của $BD$ $ \Rightarrow BD \bot AC$(vô lý).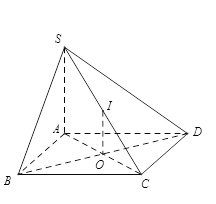

Câu 12 :

Dãy số nào sau đây có giới hạn $0$?

A

${u_n} = \dfrac{n}{2}$
B

${u_n} = \dfrac{2}{n}$
C

${u_n} = n$
D

${u_n} = \sqrt n $

Đáp án : B

Lời giải chi tiết :

Dãy số $\left( {{u_n}} \right)$ mà ${u_n} = \dfrac{2}{n}$ có giới hạn $0$.

Câu 13 :

A

$\dfrac{{3{a^2}}}{8}.$
B

$\dfrac{{3{a^2}}}{2}.$
C

$\dfrac{{3{a^2}}}{4}.$
D

$\dfrac{{2{a^2}}}{3}.$

Đáp án : C

Phương pháp giải :

Sử dụng lý thuyết của đường thẳng vuông góc với mặt phẳng và bài toán tìm giao tuyến của hai mặt phẳng đồng thời việc tính toán trong tam giác, cụ thể là tính diện tích

Lời giải chi tiết :

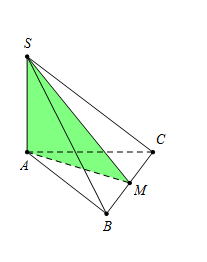Gọi $M$ là trung điểm của $BC$ thì $BC \bot AM\,\,\,\,\,\,\,\,\,\left( 1 \right).$

Hiển nhiên $AM = \dfrac{{2a\sqrt 3 }}{2} = a\sqrt 3 $.

Mà $SA \bot \left( {ABC} \right) \Rightarrow BC \bot SA\,\,\,\,\,\,\,\,\,\,\,\,\left( 2 \right).$

Từ $\left( 1 \right)\,$và $\left( 2 \right)$ suy ra $BC \bot \left( {SAM} \right) \Rightarrow \left( P \right) \equiv \left( {SAM} \right).$

$ \Rightarrow $ Thiết diện của hình chóp $S.ABC$ được cắt bởi $(P)$ chính là $\Delta SAM.$

Và $\Delta \,SAM$ vuông tại $A$ nên ${S_{\Delta SAM}} = \dfrac{1}{2}SA.AM $ $= \dfrac{1}{2}.\dfrac{{a\sqrt 3 }}{2}.a\sqrt 3 = \dfrac{{3{a^2}}}{4}.$

Câu 14 :

Cho dãy số $\left( {{x_n}} \right)$ với ${x_n} = \dfrac{{an + 4}}{{n + 2}}$. Dãy số $\left( {{x_n}} \right)$ là dãy số tăng khi:

A

a = 2
B

a > 2
C

a < 2
D

a > 1

Đáp án : B

Phương pháp giải :

Xét hiệu $A={x_{n + 1}} - {x_n} $ và kết luận:

+ Nếu $A>0$ thì dãy tăng.

+ Nếu $A<0$ thì dãy giảm.

Lời giải chi tiết :

Ta có ${x_{n + 1}} = \dfrac{{a\left( {n + 1} \right) + 4}}{{\left( {n + 1} \right) + 2}} = \dfrac{{a\left( {n + 1} \right) + 4}}{{n + 3}}.$

Xét hiệu

$\begin{array}{l}{x_{n + 1}} - {x_n} = \dfrac{{a\left( {n + 1} \right) + 4}}{{n + 3}} - \dfrac{{an + 4}}{{n + 2}} = \dfrac{{\left( {an + a + 4} \right)\left( {n + 2} \right) - \left( {an + 4} \right)\left( {n + 3} \right)}}{{\left( {n + 3} \right)\left( {n + 2} \right)}}\\ = \dfrac{{a{n^2} + 2an + an + 2a + 4n + 8 - a{n^2} - 3an - 4n - 12}}{{\left( {n + 3} \right)\left( {n + 2} \right)}}\\ = \dfrac{{2a - 4}}{{\left( {n + 3} \right)\left( {n + 2} \right)}}\end{array}$

Để $\left( {{x_n}} \right)$ là dãy số tăng khi và chỉ khi ${x_{n + 1}} - {x_n} > 0\,\,\forall n \ge 1 \Rightarrow 2a - 4 > 0 \Leftrightarrow a > 2.$

Câu 15 :

Cho cấp số nhân $\left( {{u_n}} \right)$, biết: ${u_1} = 3,{u_5} = 48$ . Lựa chọn đáp án đúng.

A

${u_3} = 12.\,\,\,\,$
B

${u_3} = - 12.$
C

${u_3} = 16.$
D

${u_3} = - 16.$

Đáp án : A

Phương pháp giải :

Sử dụng công thức số hạng tổng quát của cấp số nhân: ${u_n} = {u_1}{q^{n - 1}},\forall n \ge 2$

Lời giải chi tiết :

Ta có: ${u_5} = {u_1}.{q^4} \Leftrightarrow 48 = 3.{q^4} \Leftrightarrow {q^4} = 16 $ $\Leftrightarrow {q^2} = 4 \Rightarrow {u_3} = {u_1}.{q^2} = 3.4 = 12$

Câu 16 :

Cho hình chóp $S.ABCD$ có $SA \bot \left( {ABCD} \right)$ và $AB \bot BC$. Dựng $AH$ là đường cao của $\Delta SAB$. Khẳng định nào sau đây sai?

A

$SA \bot CD$.
B

$AH \bot BC$.
C

$AH \bot \left( {SCD} \right)$.
D

$AH \bot SC$.

Đáp án : C

Lời giải chi tiết :

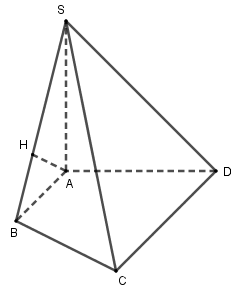Do $SA \bot \left( {ABCD} \right)$ nên $SA \bot CD$ hay A đúng.

Do $\left\{ \begin{array}{l}BC \bot AB\\BC \bot SA\end{array} \right. \Rightarrow BC \bot \left( {SAB} \right)$ $ \Rightarrow BC \bot AH$ nên B đúng.

Lại có $\left\{ \begin{array}{l}AH \bot SB\\AH \bot BC\end{array} \right. \Rightarrow AH \bot \left( {SBC} \right) \Rightarrow AH \bot SC$ nên D đúng.

Do $AH \bot \left( {SBC} \right)$ nên nó không thể vuông góc với $\left( {SCD} \right)$ nên C sai.

Câu 17 :

Dãy số nào trong các dãy số sau không phải là cấp số nhân:

A

${u_n} = {5^n}$
B

${u_n} = {\left( {2 - \sqrt 3 } \right)^{n + 1}}$
C

${u_n} = 5n + 1$
D

${u_n} = {4^n}$

Đáp án : C

Phương pháp giải :

- Bước 1: Tính $q = \dfrac{{{u_{n + 1}}}}{{{u_n}}},\forall n \ge 1$.

- Bước 2: Kết luận:

+ Nếu $q$ là số không đổi thì dãy $\left( {{u_n}} \right)$ là cấp số nhân.

+ Nếu $q$ thay đổi theo $n$ thì dãy $\left( {{u_n}} \right)$ không là cấp số nhân.

Lời giải chi tiết :

Ta có ${u_n} = {5^n}$ nên ${u_{n + 1}} = {5^{n + 1}} \Rightarrow \dfrac{{{u_{n + 1}}}}{{{u_n}}} = \dfrac{{{5^{n + 1}}}}{{{5^n}}} = 5$ không đổi $\forall n \ge 1$ .

Vậy dãy số $\left( {{u_n}} \right)$ có ${u_n} = {5^n}$là cấp số nhân.

Tương tự ta cũng có dãy số ở đáp án D là cấp số nhân.

Ta có ${u_n} = 2{( - \sqrt 3 )^{n + 1}}$ nên ${u_{n + 1}} = 2{( - \sqrt 3 )^{n + 2}} = ( - \sqrt 3 ){u_n} \Rightarrow \dfrac{{{u_{n + 1}}}}{{{u_n}}} = ( - \sqrt 3 )$không đổi $\forall n \ge 1$ .

Vậy dãy số $\left( {{u_n}} \right)$có ${u_n} = 2{( - \sqrt 3 )^{n + 1}}$ là cấp số nhân.

Ta có ${u_n} = 5n + 1$ nên ${u_1} = 8;{u_2} = 13;{u_3} = 18 \Rightarrow \dfrac{{{u_2}}}{{{u_1}}} \ne \dfrac{{{u_3}}}{{{u_2}}}$

Vậy dãy số $\left( {{u_n}} \right)$không là cấp số nhân.

Câu 18 :

Cho cấp số cộng $\left( {{u_n}} \right)$ với $\left\{ \begin{array}{l}{u_3} + {u_5} = 5\\{u_3}.{u_5} = 6\end{array} \right..$ Tìm số hạng đầu của cấp số cộng.

A

$\left[ \begin{array}{l}{u_1} = 1\\{u_1} = 4\end{array} \right.$
B

$\left[ \begin{array}{l}{u_1} = 1\\{u_1} = - 4\end{array} \right.$
C

$\left[ \begin{array}{l}{u_1} = - 1\\{u_1} = 4\end{array} \right.$
D

$\left[ \begin{array}{l}{u_1} = - 1\\{u_1} = 1\end{array} \right.$

Đáp án : A

Phương pháp giải :

Tìm hai số khi biết tổng $S$ và tích $P$ là nghiệm của phương trình ${X^2} - SX + P = 0$.

Sử dụng công thức số hạng tổng quát của CSC ${u_n} = {u_1} + \left( {n - 1} \right)d$

Lời giải chi tiết :

$\left\{ \begin{array}{l}{u_3} + {u_5} = 5\\{u_3}.{u_5} = 6\end{array} \right. \Rightarrow {u_3},{u_5}$ là nghiệm của phương trình ${X^2} - 5X + 6 = 0 \Rightarrow \left[ \begin{array}{l}X = 3\\X = 2\end{array} \right. \Rightarrow \left[ \begin{array}{l}\left\{ \begin{array}{l}{u_3} = 3\\{u_5} = 2\end{array} \right.\\\left\{ \begin{array}{l}{u_3} = 2\\{u_5} = 3\end{array} \right.\end{array} \right.$

TH1 : $\left\{ \begin{array}{l}{u_3} = 3\\{u_5} = 2\end{array} \right. \Rightarrow \left\{ \begin{array}{l}{u_1} + 2d = 3\\{u_1} + 4d = 2\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{u_1} = 4\\d = - \dfrac{1}{2}\end{array} \right.$

TH2 : $\left\{ \begin{array}{l}{u_3} = 2\\{u_5} = 3\end{array} \right. \Rightarrow \left\{ \begin{array}{l}{u_1} + 2d = 2\\{u_1} + 4d = 3\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{u_1} = 1\\d = \dfrac{1}{2}\end{array} \right.$

Vậy $\left[ \begin{array}{l}{u_1} = 1\\{u_1} = 4\end{array} \right.$.

Câu 19 :

Cho dãy số $\left( {{a_n}} \right)$ xác định bởi ${a_n} = 2017\sin \dfrac{{n\pi }}{2} + 2018\cos \dfrac{{n\pi }}{3}$. Mệnh đề nào dưới đây là mệnh đề đúng?

A

${a_{n + 6}} = {a_n},\forall n \in {\mathbb{N}^*}$.
B

${a_{n + 9}} = {a_n},\forall n \in {\mathbb{N}^*}$.
C

${a_{n + 12}} = {a_n},\forall n \in {\mathbb{N}^*}$.
D

${a_{n + 15}} = {a_n},\forall n \in {\mathbb{N}^*}$.

Đáp án : C

Phương pháp giải :

Kiểm tra từng phương án đến khi tìm được đáp án đúng.

Lời giải chi tiết :

+ Ta có ${a_{n + 6}} = 2017\sin \dfrac{{\left( {n + 6} \right)\pi }}{2} $ $+ 2018\cos \dfrac{{\left( {n + 6} \right)\pi }}{3} $ $= - 2017\sin \dfrac{{n\pi }}{2} + 2018\cos \dfrac{{n\pi }}{3} \ne {a_n}$

+ Ta có ${a_{n + 9}} = 2017\sin \dfrac{{\left( {n + 9} \right)\pi }}{2} $ $+ 2018\cos \dfrac{{\left( {n + 9} \right)\pi }}{3} $ $= 2017\cos \dfrac{{n\pi }}{2} - 2018\cos \dfrac{{n\pi }}{3} \ne {a_n}$.

+ Ta có ${a_{n + 12}} = 2017\sin \dfrac{{\left( {n + 12} \right)\pi }}{2} $ $+ 2018\cos \dfrac{{\left( {n + 12} \right)\pi }}{3} $ $= 2017\sin \dfrac{{n\pi }}{2} + 2018\cos \dfrac{{n\pi }}{3} = {a_n}$.

+ Ta có ${a_{n + 15}} = 2017\sin \dfrac{{\left( {n + 15} \right)\pi }}{2} $ $+ 2018\cos \dfrac{{\left( {n + 15} \right)\pi }}{3}$ $ = -2017\cos \dfrac{{n\pi }}{2} - 2018\cos \dfrac{{n\pi }}{3} \ne {a_n}$.

Câu 20 :

A

$S = \dfrac{{5{a^2}\sqrt 6 }}{{12}}.$
B

$S = \dfrac{{5{a^2}\sqrt 6 }}{{18}}.$
C

$S = \dfrac{{5{a^2}\sqrt 6 }}{3}.$
D

$S = \dfrac{{5{a^2}\sqrt 6 }}{5}.$

Đáp án : B

Phương pháp giải :

Sử dụng lý thuyết của đường thẳng vuông góc với mặt phẳng và bài toán tìm giao tuyến của hai mặt phẳng đồng thời việc tính toán trong tam giác, tứ giác cụ thể là tính diện tích đa giác

Lời giải chi tiết :

Ta có AD vuông góc với SA và AB$ \Rightarrow AD \bot mp\,\,\left( {SAB} \right) \Rightarrow AD \bot SB.$

Vẽ đường cao AH trong tam giác SAB

Lại có AD và AH qua A và vuông góc với SB.

Vậy mặt phẳng $\left( \alpha \right)$ chính là mặt phẳng (AHD)

Mặt khác AD // mp(SBC) mà $AD \subset mp\,\,\left( {AHD} \right)$

Vậy mặt phẳng (SBC) cắt mặt phẳng (AHD) theo giao tuyến HK // AD.

Do đó mặt cắt là hình thang ADKH mà $AD \bot mp\,\,\left( {SAB} \right)$$ \Rightarrow \,AD \bot AH.$

Suy ra tứ giác ADKH là hình thang vuông.

Tam giác SAB vuông $ \Rightarrow \,\,AH = \dfrac{{SA.AB}}{{SC}} = \dfrac{{a\sqrt 2 .a}}{{a\sqrt 3 }} = \dfrac{{a\sqrt 6 }}{3}.$ Và $S{A^2} = SH.HB\,\, \Rightarrow \,\,SH = \dfrac{{S{A^2}}}{{SB}} = \dfrac{{2{a^2}}}{{a\sqrt 3 }} = \dfrac{{2a\sqrt 3 }}{3}.$

Ta có $HK$//$BC$$ \Rightarrow \,\,\dfrac{{HK}}{{BC}} = \dfrac{{SH}}{{SB}}\,\, \Rightarrow \,\,HK = \dfrac{{SH.BC}}{{SB}} = \dfrac{{\dfrac{{2a\sqrt 3 }}{3}.a}}{{a\sqrt 3 }} = \dfrac{{2a}}{3}.$

Do đó ${S_{ADKH}} = \dfrac{{AH}}{2}.\left( {HK + AD} \right) = \dfrac{{a\sqrt 6 }}{6}.\left( {\dfrac{{2a}}{3} + a} \right) = \dfrac{{a\sqrt 6 }}{6}.\dfrac{{5a}}{3} = \dfrac{{5{a^2}\sqrt 6 }}{{18}}.$

Câu 21 :

A

$30^\circ $.
B

$45^\circ $.
C

$60^\circ $.
D

$75^\circ $.

Đáp án : A

Phương pháp giải :

- Xác định góc giữa $SC$ và $\left( {ABCD} \right)$: là góc giữa $SC$ và hình chiếu của nó trên $\left( {ABCD} \right)$.

- Tính góc ở trên bởi tỉ số lượng giác trong tam giác vuông.

Lời giải chi tiết :

Ta có: $SA \bot \left( {ABCD} \right) \Rightarrow SA \bot AC$

$ \Rightarrow \widehat {\left( {SC;\left( {ABCD} \right)} \right)} = \widehat {\left( {SC,AC} \right)} = \widehat {SCA} = \alpha $

$ABCD$ là hình vuông cạnh $a$ $ \Rightarrow AC = a\sqrt 2 ,SA = \dfrac{{a\sqrt 6 }}{3}$ $ \Rightarrow \tan \alpha = \dfrac{{SA}}{{AC}} = \dfrac{{\sqrt 3 }}{3} \Rightarrow \alpha = 30^\circ $.

Câu 22 :

Chọn mệnh đề sai:

A

$\lim n = + \infty $
B

$\lim \sqrt n = + \infty $
C

$\lim \sqrt[3]{n} = + \infty $
D

$\lim \dfrac{1}{n} = + \infty $

Đáp án : D

Lời giải chi tiết :

Ta có: $\lim n = + \infty ,\lim \sqrt n = + \infty ,$ $\lim \sqrt[3]{n} = + \infty ,$ $\lim \dfrac{1}{n} = 0 $

Vậy chỉ có đáp án D là sai.

Câu 23 :

Cho tứ diện đều $ABCD$ có tam giác $BCD$ đều,$AD = AC$. Giá tri của $\cos \left( {\overrightarrow {AB} ,\overrightarrow {CD} } \right)$là:

A

$\dfrac{1}{2}$
B

$0$
C

$ - \dfrac{1}{2}$.
D

$\dfrac{{\sqrt 3 }}{2}$.

Đáp án : B

Phương pháp giải :

Sử dụng công thức tính $\cos \left( {\overrightarrow a ,\overrightarrow b } \right) = \dfrac{{\overrightarrow a .\overrightarrow b }}{{\left| {\overrightarrow a } \right|.\left| {\overrightarrow b } \right|}}$.

Lời giải chi tiết :

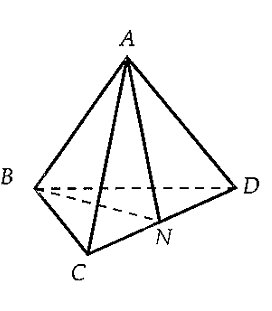Gọi $N$ là trung điểm của $CD$. Tam giác đều $BCD$ nên $BN \bot CD$. Tam giác $ACD$cân tại $A$ nên $AN \bot CD$ ta có:

$\overrightarrow {AB} .\overrightarrow {CD} = \left( {\overrightarrow {AN} + \overrightarrow {NB} } \right).\overrightarrow {CD} = \overrightarrow {AN} .\overrightarrow {CD} + \overrightarrow {NB} .\overrightarrow {CD} = 0 \Rightarrow c{\rm{os}}\left( {\overrightarrow {AB} ,\overrightarrow {CD} } \right) = \dfrac{{\overrightarrow {AB} .\overrightarrow {CD} }}{{\left| {\overrightarrow {AB} } \right|.\left| {\overrightarrow {CD} } \right|}} = 0$

Câu 24 :

A

Hình thang
B

Hình bình hành
C

Hình chữ nhật
D

Hình vuông

Đáp án : C

Phương pháp giải :

- Xác đinh thiết diện của hình tứ diện khi cắt bởi mặt phẳng $\left( P \right)$.

- Xác định góc giữa hai đường thẳng $MN,MQ$ bằng cách sử dụng tính chất $\left\{ \begin{array}{l}a//a'\\b//b'\end{array} \right. \Rightarrow \widehat {\left( {a,b} \right)} = \widehat {\left( {a',b'} \right)}$

Lời giải chi tiết :

Ta có: $\left\{ \begin{array}{l}\left( {MNPQ} \right){\rm{//}}AB\\\left( {MNPQ} \right) \cap \left( {ABC} \right) = MQ\end{array} \right. $ $\Rightarrow MQ{\rm{//}}AB$

Tương tự ta có: $MN{\rm{//}}CD,\,\,NP{\rm{//}}AB,\,\,QP{\rm{//}}C{\rm{D}}$.

Do đó tứ giác $MNPQ$ là hình bình hành

lại có $MN \bot MQ\left( {do\,AB \bot CD\,} \right)$.

Vậy tứ giác $MNPQ$ là hình chữ nhật.

Câu 25 :

Cho tứ diện $OABC$ có $OA,OB,OC$ đôi một vuông góc với nhau. Gọi $H$ là hình chiếu của $O$ trên mặt phẳng $\left( {ABC} \right)$. Xét các mệnh đề sau :

I. Vì $OC \bot OA,OC \bot OB$ nên $OC \bot \left( {OAB} \right)$.

II. Do $AB \subset \left( {OAB} \right)$nên $AB \bot OC.{\rm{ }}\left( 1 \right)$

III. Có $OH \bot \left( {ABC} \right)$ và $AB \subset \left( {ABC} \right)$nên $AB \bot OH.{\rm{ }}\left( 2 \right)$

IV. Từ $\left( 1 \right)$ và $\left( 2 \right) \Rightarrow AB \bot \left( {OCH} \right)$

Số mệnh đề đúng trong các mệnh đề trên là:

A

$4$.
B

$3$.
C

$2$.
D

$1$.

Đáp án : A

Phương pháp giải :

Sử dụng điều kiện đường thẳng vuông góc mặt phẳng để xét tính đúng, sai cho từng mệnh đề.

Lời giải chi tiết :

Ta có:

$\left\{ \begin{array}{l}OC \bot OA\\OC \bot OB\\OA \cap OB = O\\OA,OB \subset \left( {OAB} \right)\end{array} \right. \Rightarrow OC \bot \left( {OAB} \right)$.

Vậy $I$ đúng.

$\left\{ \begin{array}{l}OC \bot \left( {OAB} \right)\\AB \subset \left( {OAB} \right)\end{array} \right. \Rightarrow AB \bot OC$.

Vậy $II$ đúng.

$\left\{ \begin{array}{l}OH \bot \left( {ABC} \right)\\AB \subset \left( {ABC} \right)\end{array} \right. \Rightarrow AB \bot OH$.

Vậy $III$ đúng.

$\left\{ {\begin{array}{*{20}{c}}{AB \bot OC}\\{AB \bot OH}\\\begin{array}{l}OC \cap OH = O\\OC,OH \subset \left( {OCH} \right)\end{array}\end{array}} \right. \Rightarrow AB \bot \left( {OCH} \right)$.

Vậy $IV$ đúng.

Câu 26 :

A

$k \ne p.$
B

$k \ge p.$
C

$k = p.$
D

$k < p.$

Đáp án : B

Lời giải chi tiết :

Ở bước 2 ta cần giả sử mệnh đề đúng với $n = k$ với $k \ge p$.

Câu 27 :

A

$S = \dfrac{{{a^2}\sqrt {3{b^2} - 2ab} }}{{4b}}$
B

$S = \dfrac{{{a^2}\sqrt {3{b^2} - 2ab} }}{{2b}}$
C

$S = \dfrac{{{a^2}\sqrt {3{b^2} + 2ab} }}{{2b}}$
D

$S = \dfrac{{{a^2}\sqrt {3{b^2} + 2ab} }}{{4b}}$

Đáp án : A

Phương pháp giải :

Lời giải chi tiết :

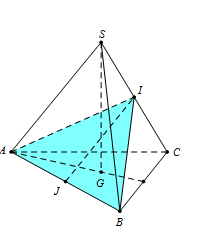Kẻ $AI \bot SC$, ta dễ dàng chứng minh được $\Delta SAI = \Delta SBI\,\,\left( {c.g.c} \right) \Rightarrow \widehat {SIA} = \widehat {SIB} = {90^0} \Rightarrow BI \bot SC$

$ \Rightarrow SC \bot \left( {ABI} \right)$. Thiết diện là tam giác $AIB.$

Ta có $AI = AC\sin \widehat {ACS} = a.\sqrt {1 - {{\cos }^2}\widehat {ACS}} = a.\sqrt {1 - \left( {\dfrac{{{a^2} + {b^2} - {b^2}}}{{2ab}}} \right)} = a\sqrt {1 - \dfrac{a}{{2b}}} .$

Gọi $J$ là trung điểm của $AB.$ Dễ thấy tam giác $AIB$ cân tại $I,$ suy ra $IJ \bot AB$

$ \Rightarrow IJ = \sqrt {A{I^2} - A{J^2}} = \sqrt {{a^2}\left( {1 - \dfrac{a}{{2b}}} \right) - \dfrac{{{a^2}}}{4}} = a\sqrt {\dfrac{3}{4} - \dfrac{a}{{2b}}} = \dfrac{a}{{2b}}\sqrt {3{b^2} - 2ab} $

Do đó: $S = \dfrac{1}{2}AB.IJ = \dfrac{{{a^2}\sqrt {3{b^2} - 2ab} }}{{4b}}$

Câu 28 :

Giá trị $\lim \dfrac{{\sin \left( {n!} \right)}}{{{n^2} + 1}}$ bằng

A

$0.$
B

$1.$
C

$ + \infty .$
D

$2.$

Đáp án : A

Phương pháp giải :

Cho hai dãy số $\left( {{u_n}} \right),\left( {{v_n}} \right)$. Nếu $\left| {{u_n}} \right| \le {v_n}$ với mọi $n$ và $\lim {v_n} = 0$ thì $\lim {u_n} = 0$.

Lời giải chi tiết :

Ta có $\left| {\dfrac{{\sin \left( {n!} \right)}}{{{n^2} + 1}}} \right| \le \dfrac{1}{{{n^2} + 1}}$ mà $\lim \dfrac{1}{{{n^2} + 1}} = 0$ nên chọn đáp án A.

Câu 29 :

Cho tứ diện $ABCD$ đều. Gọi $\alpha $ là góc giữa $AB$ và $mp(BCD)$. Chọn khẳng định đúng trong các khẳng định sau?

A

$\cos \alpha = \dfrac{{\sqrt 3 }}{3}$.
B

$\cos \alpha = \dfrac{{\sqrt 3 }}{4}$.
C

$\cos \alpha = 0$.
D

$\cos \alpha = \dfrac{{\sqrt 3 }}{2}$.

Đáp án : A

Phương pháp giải :

- Hình chiếu của $A$ trên $mp\left( {BCD} \right)$ là trọng tâm $H$ của tam giác $BCD$.

- Góc giữa $AB$ và mặt đáy là góc giữa $AB$ và $BH$.

Lời giải chi tiết :

Gọi $H$ là hình chiếu của $A$ lên $mp(BCD)$, $a$ là độ dài cạnh của tứ diện $ABCD$.

Ta có $\alpha = \widehat {ABH},BH = \dfrac{{a\sqrt 3 }}{3} \Rightarrow \cos \alpha = \dfrac{{BH}}{{AB}} = \dfrac{{\sqrt 3 }}{3}$.

Câu 30 :

A

Ba số ${x^2},{y^2},{z^2}$ theo thứ tự lập thành cấp số cộng.
B

Ba số ${y^2},{z^2},{x^2}$ theo thứ tự lập thành cấp số cộng.
C

Ba số ${y^2},{x^2},{z^2}$ theo thứ tự lập thành cấp số cộng.
D

Ba số ${z^2},{y^2},{x^2}$ theo thứ tự lập thành cấp số cộng.

Đáp án : C

Phương pháp giải :

Sử dụng tính chất của cấp số cộng ${u_{n - 1}} + {u_{n + 1}} = 2{u_n}$

Lời giải chi tiết :

Ta có

$\dfrac{1}{{x + y}} + \dfrac{1}{{z + x}} = 2\dfrac{1}{{y + z}} \Rightarrow yz + {z^2} + xy + xz + xy + xz + {y^2} + yz = 2\left( {xz + {x^2} + yz + xy} \right) \Leftrightarrow {z^2} + {y^2} = 2{x^2}$

Vậy ba số ${y^2},{x^2},{z^2}$ theo thứ tự lập thành cấp số cộng.

Câu 31 :

Cho hình chóp $SABC$ có $SA \bot \left( {ABC} \right).$ Gọi $H,{\rm{ }}K$ lần lượt là trực tâm các tam giác $SBC$ và$ABC$. Mệnh đề nào sai trong các mệnh đề sau?

A

$BC \bot \left( {SAH} \right).$
B

$HK \bot \left( {SBC} \right).$
C

$BC \bot \left( {SAB} \right).$
D

$SH,AK$ và $BC$ đồng quy.

Đáp án : C

Phương pháp giải :

Sử dụng điều kiện đường thẳng vuông góc với mặt phẳng để xét tính đúng, sai của các đáp án.

Lời giải chi tiết :

Ta có$BC \bot SA,\,BC\, \bot SH\,\, \Rightarrow \,BC \bot (SAH)$

Ta có $CK \bot AB,CK \bot SA \Rightarrow CK \bot (SAB)$ hay $CK \bot SB$

Mặt khác có $CH \bot SB$ nên $SB \bot (CHK)$ hay $SB \bot HK$.

Ta có:

$\left\{ \begin{array}{l}
BK \bot AC\\
BK \bot SA
\end{array} \right. $ $\Rightarrow BK \bot \left( {SAC} \right) \Rightarrow BK \bot SC$

Mà $BH \bot SC$ nên $SC \bot (BHK)$ nên $SC \bot HK$.

Do đó $HK \bot (SBC)$.

Gọi $M$ là giao điểm của $SH$ và $BC$. Do $BC \bot (SAH)\,\, \Rightarrow BC \bot AM$ hay đường thẳng

$AM$ trùng với đường thẳng $AK$. Hay $SH,AK$ và $BC$ đồng quy.

Do đó $BC \bot \left( {SAB} \right)$ là sai.

Câu 32 :

A

${a_{2018}} = {a_2}$
B

${a_{2018}} = {a_1}$
C

${a_{2018}} = {a_3}$
D

${a_{2018}} = {a_4}$

Đáp án : A

Phương pháp giải :

Đây là dãy số có tính chất tuần hoàn, xác định tính chất tuần hoàn đó và suy ra đáp án.

Lời giải chi tiết :

Sáu số hạng đầu tiên của dãy số đó là

$\begin{array}{l}{a_1} = 1\\{a_2} = - \dfrac{3}{2} + \dfrac{5}{2} + 1 = 2\\{a_3} = - \dfrac{3}{2}.4 + \dfrac{5}{2}.2 + 1 = 0\\{a_4} = - \dfrac{3}{2}.0 + \dfrac{5}{2}.0 + 1 = 1\\{a_5} = - \dfrac{3}{2} + \dfrac{5}{2} + 1 = 2\\{a_6} = - \dfrac{3}{2}.4 + \dfrac{5}{2}.2 + 1 = 0\end{array}$

Ta thấy cứ sau $3$ số hạng, dãy số trên sẽ bị lặp lại, do đó ta dự đoán ${a_{n + 3}} = {a_n}\,\,\forall n \ge 1$

Chứng minh khẳng định trên bằng phương pháp quy nạp toán học :

Đẳng thức đúng với $n = 1,{a_1} = {a_4} = 1$.

Giả sử đẳng thức đúng với $n = k$, tức là ${a_{k + 3}} = {a_k}$ , ta cần chứng minh đẳng thức đúng với $n = k + 1$, tức là cần chứng minh ${a_{k + 4}} = {a_{k + 1}}$

Ta có :

$\begin{array}{l}{a_{k + 4}} = - \dfrac{3}{2}a_{k + 3}^2 + \dfrac{5}{2}{a_{k + 3}} + 1\\{a_{k + 1}} = - \dfrac{3}{2}a_k^2 + \dfrac{5}{2}{a_k} + 1\end{array}$

Mà ${a_{k + 3}} = {a_k} \Rightarrow {a_{k + 4}} = {a_{k + 1}}$, vậy ${a_{n + 3}} = {a_n}\,\,\forall n \ge 1$.

Tổng quát ${a_{3n + m}} = {a_m},\forall m,n \in {N^*}$

Ta lại có $2018 = 3.672 + 2$.

Từ đó ta suy ra ${a_{2018}} = {a_{3.672+2}}={a_{2}}$

Câu 33 :

A

$98$ ô
B

$100$ ô
C

$102$ ô
D

$104$ ô

Đáp án : B

Phương pháp giải :

Dãy số $\left( {{u_n}} \right)$ với ${u_n}$ là số hạt dẻ ở ô thứ n là một cấp số cộng có ${u_1} = 7$ và công sai $d = 5$. Sử dụng công thức tổng n số hạng đầu tiên của CSC: ${S_n} = \dfrac{{n\left( {2{u_1} + \left( {n - 1} \right)d} \right)}}{2}$

Lời giải chi tiết :

Gọi ${u_n}$ là số hạt dẻ ở ô thứ $n$ . Khi đó ta có ${u_1} = 7$ và ${u_{n + 1}} = {u_n} + 5,\forall n \ge 1.$

Dãy số $\left( {{u_n}} \right)$ là cấp số cộng với ${u_1} = 7$ và công sai $d = 5$ nên ta có

${S_n} = \dfrac{{n\left[ {2{u_1} + \left( {n - 1} \right)d} \right]}}{2} = \dfrac{{n\left[ {2.7 + \left( {n - 1} \right)5} \right]}}{2} = \dfrac{{5{n^2} + 9n}}{2}$

Theo giả thiết ta có ${S_n} = 25450$ $ \Rightarrow \dfrac{{5{n^2} + 9n}}{2} = 25450 \Leftrightarrow n = 100$

Vậy bàn cờ có $100$ ô.

Câu 34 :

A

${h_n} = 0,18n + 0,32\,\,\left( m \right)$
B

${h_n} = 0,18n + 0,5\,\,\left( m \right)$
C

${h_n} = 0,5n + 0,18\,\,\left( m \right)$
D

${h_n} = 0,5n - 0,32\,\,\left( m \right)$

Đáp án : A

Phương pháp giải :

- Dãy số $\left( {{h_n}} \right)$ với ${h_n}$ là độ cao của bậc thứ $n$ so với mặt sân là một cấp số cộng có ${u_1} = 0,5$ và công sai $d = 0,18$ .

- Sử dụng công thức số hạng tổng quát của CSC: ${h_n} = {h_1}+\left( {n - 1} \right)d$

Lời giải chi tiết :

Ký hiệu ${h_n}$ là độ cao bậc $n$ so với mặt sân. Khi đó ta có ${h_{n + 1}} = {h_n} + 0,18\,\,\left( m \right)$, trong đó ${h_1} = 0,5 m$ là độ cao của bậc 1 so với mặt sân.

Dãy số $\left( {{h_n}} \right)$ là cấp số cộng có ${h_1} = 0,5$ và công sai $d = 0,18$. Suy ra số hạng tổng quát của cấp số cộng này là ${h_n} = {h_1} + \left( {n - 1} \right)d= 0,5+ \left( {n - 1} \right)0,18 $$ = 0,18n + 0,32$ (mét).

Câu 35 :

A

$2,{22.10^{ - 15}}$
B

$2,{21.10^{ - 15}}$
C

$2,{20.10^{ - 15}}$
D

$2,{23.10^{ - 15}}$

Đáp án : A

Phương pháp giải :

Sử dụng công thức số hạng tổng quát của cấp số nhân để tính số hạng ${u_{53}}$.

Lời giải chi tiết :

Gọi ${u_n}$ là khối lượng còn lại của $20$ gam poloni sau $n$ chu kì bán rã.

Ta có $7314$ ngày gồm $\dfrac{{7314}}{{138}} = 53$ chu kì bán rã.

Do đó ta cần tính ${u_{53}}$

Theo giả thiết của bài toán thì $\left( {{u_n}} \right)$ là một cấp số nhân với số hạng đầu ${u_1} = \dfrac{{20}}{2} = 10;q = \dfrac{1}{2}$

Do đó ${u_{53}} = 10{\left( {\dfrac{1}{2}} \right)^{52}} \approx 2,{22.10^{ - 15}}$

Câu 36 :

A

$10.$
B

$20.$
C

$15.$
D

$16.$

Đáp án : C

Phương pháp giải :

Lời giải chi tiết :

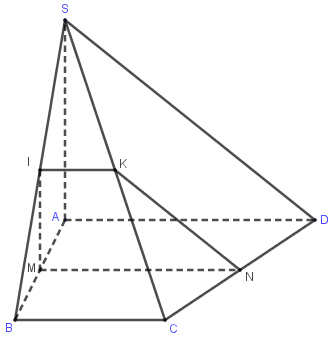Do $\left( P \right) \bot AB \Rightarrow \left( P \right)\parallel SA.$

Gọi $I$ là trung điểm của $SB \Rightarrow MI\parallel SA \Rightarrow MI \subset \left( P \right).$

Gọi $N$ là trung điểm của $CD \Rightarrow MN \bot AB \Rightarrow MN \subset \left( P \right).$

Gọi $K$ là trung điểm của $SC \Rightarrow IK\parallel BC$,

Mà $MN\parallel BC \Rightarrow MN\parallel IK \Rightarrow IK \subset \left( P \right).$

Vậy thiết diện của $(P)$ và hình chóp là hình thang $MNKI$ vuông tại $M$ và $I.$

Ta có: $MI$ là đường trung bình của tam giác $SAB$ $ \Rightarrow MI = \dfrac{1}{2}SA = 3.$

$IK$ là đường trung bình của tam giác $SBC$ $ \Rightarrow IK = \dfrac{1}{2}BC = 3.$

$MN$ là đường trung bình của hình thang $ABCD$ $ \Rightarrow MN = \dfrac{1}{2}\left( {AD + BC} \right) = 7.$

Vậy ${S_{MNKI}} = \dfrac{{IK + MN}}{2}.MI = \dfrac{{3 + 7}}{2}.3 = 15.$

Câu 37 :

Cho hình hộp $ABCD.A'B'C'D'$ có tất cả các cạnh đều bằng nhau. Trong các mệnh đề sau, mệnh đề nào có thể sai?

A

$A'C' \bot BD$.
B

$BB' \bot BD$.
C

$A'B \bot DC'$.
D

$BC' \bot A'D$.

Đáp án : B

Phương pháp giải :

Sử dụng tính chất $\left\{ \begin{array}{l}a \bot b\\b//c\end{array} \right. \Rightarrow a \bot c$

Lời giải chi tiết :

A đúng vì:

$\left\{ \begin{array}{l}A'C' \bot B'D'\\B'D'{\rm{ // }}BD\end{array} \right. \Rightarrow A'C' \bot BD$.

C đúng vì: $\left\{ \begin{array}{l}A'B \bot AB'\\AB'{\rm{ // }}DC'\end{array} \right. \Rightarrow A'B \bot DC'$.

D đúng vì: $\left\{ \begin{array}{l}BC' \bot B'C\\B'C{\rm{ // }}A'D\end{array} \right. \Rightarrow BC' \bot A'D$.

Câu 38 :

Cho dãy số $({u_n})$ xác định bởi $\left\{ \begin{align} & u_{1}=2 \\ & {u_{n+1}}=\dfrac{{{u}_{n}}+1}{2},(n\ge 1) \end{align} \right.$ Khi đó mệnh đề nào sau đây là đúng?

A

Dãy $({u_n})$là dãy giảm tới $1$ khi $n \to + \infty $.
B

Dãy $({u_n})$là dãy tăng tới $1$ khi $n \to + \infty $.
C

Không tồn tại giới hạn của dãy $({u_n})$.
D

Cả 3 đáp án trên đều sai

Đáp án : A

Phương pháp giải :

- Tính ${u_2},\,{u_3},...$, từ đó dự đoán công thức tổng quát của dãy số.

- Rút ra nhận xét.

Lời giải chi tiết :

$\begin{array}{l}{u_2} = \dfrac{{2 + 1}}{2} = \dfrac{3}{2} = \dfrac{{{2^1} + 1}}{{{2^1}}}\\{u_3} = \dfrac{{\dfrac{3}{2} + 1}}{2} = \dfrac{5}{4} = \dfrac{{{2^2} + 1}}{{{2^2}}}\\{u_4} = \dfrac{{\dfrac{5}{4} + 1}}{2} = \dfrac{9}{8} = \dfrac{{{2^3} + 1}}{{{2^3}}}\end{array}$

Chứng minh bằng quy nạp: ${u_{n + 1}} = \dfrac{{{2^n} + 1}}{{{2^n}}},\,\,\forall n = 1;2;...\,\,\,\,(*)$:

* Với $n = 1$: ${u_2} = \dfrac{{{u_1} + 1}}{2} = \dfrac{{2 + 1}}{2} = \dfrac{{{2^1} + 1}}{{{2^1}}}$ : (*) đúng

* Giả sử (*) đúng với $n = k \ge 1$, tức là ${u_k} = \dfrac{{{2^k} + 1}}{{{2^k}}}$ ta chứng minh (*) đúng với $n = k + 1$ , tức là cần chứng minh ${u_{k + 1}} = \dfrac{{{2^{k + 1}} + 1}}{{{2^{k + 1}}}}$

Ta có : ${u_{k + 1}} = \dfrac{{{u_k} + 1}}{2} = \dfrac{{\dfrac{{{2^k} + 1}}{{{2^k}}} + 1}}{2} = \dfrac{{\dfrac{{{2^k} + 1 + {2^k}}}{{{2^k}}}}}{2} = \dfrac{{{{2.2}^k} + 1}}{{{2^{k + 1}}}} = \dfrac{{{2^{k + 1}} + 1}}{{{2^{k + 1}}}}$

Theo nguyên lý quy nạp, ta chứng minh được (*).

Như vậy, công thức tổng quát của dãy $({u_n})$là: ${u_n} = \dfrac{{{2^{n - 1}} + 1}}{{{2^{n - 1}}}} = 1 + \dfrac{1}{{{2^{n - 1}}}},\,\,\forall n = 1;2;...\,\,\,\,(*)$

Từ (*) ta có ${u_{n + 1}} - {u_n} = 1 + \dfrac{1}{{{2^n}}} - \left( {1 + \dfrac{1}{{{2^{n - 1}}}}} \right) $ $= \dfrac{1}{{{2^n}}} - \dfrac{1}{{{2^{n + 1}}}} < 0\,\,\forall n = 1,2,... \Rightarrow \left( {{u_n}} \right)$ là dãy giảm và $\lim {u_n} = \lim \left( {1 + \dfrac{1}{{{2^{n - 1}}}}} \right) = 1 \Rightarrow $$({u_n})$ là dãy giảm tới $1$ khi $n \to + \infty $

Câu 39 :

Cho các số thực a, b thỏa $\left| a \right| < 1;\;\;\left| b \right| < 1$. Tìm giới hạn $I = \lim \dfrac{{1 + a + {a^2} + ... + {a^n}}}{{1 + b + {b^2} + ... + {b^n}}}$.

A

$ + \infty $
B

$\dfrac{{1 - a}}{{1 - b}}$
C

$\dfrac{{1 - b}}{{1 - a}}$
D

$1$

Đáp án : C

Phương pháp giải :

Nếu $\left| q \right| < 1$ thì $\mathop {\lim }\limits_{n \to + \infty } {q^n} = 0$

Lời giải chi tiết :

Ta có $1,\;a,\;{a^2},\;...,\;{a^n}$ là một cấp số nhân có công bội $a$ $ \Rightarrow 1 + a + {a^2} + ... + {a^n} = \dfrac{{1 - {a^{n + 1}}}}{{1 - a}}.$

Tương tự: $1 + b + {b^2} + ... + {b^n} = \dfrac{{1 - {b^{n + 1}}}}{{1 - b}}$

$ \Rightarrow \lim I = \lim \dfrac{{\dfrac{{1 - {a^{n + 1}}}}{{1 - a}}}}{{\dfrac{{1 - {b^{n + 1}}}}{{1 - b}}}} = \lim \left( {\dfrac{{1 - {a^{n + 1}}}}{{1 - a}}.\dfrac{{1 - b}}{{1 - {b^{n + 1}}}}} \right) = \lim \left( {\dfrac{{1 - {a^{n + 1}}}}{{1 - {b^{n + 1}}}}.\dfrac{{1 - b}}{{1 - a}}} \right) = \dfrac{{1 - b}}{{1 - a}}.$

(Vì $\left| a \right| < 1,\;\;\left| b \right| < 1$$ \Rightarrow \lim {a^{n + 1}} = \lim {b^{n + 1}} = 0$).

Câu 40 :

A

$\overrightarrow {MG} = - \dfrac{1}{6}\overrightarrow b + \dfrac{1}{3}\overrightarrow c + \dfrac{1}{3}\overrightarrow d $ .
B

$\overrightarrow {MG} = \dfrac{1}{6}\overrightarrow b + \dfrac{1}{3}\overrightarrow c + \dfrac{1}{3}\overrightarrow d $
C

$\overrightarrow {MG} = - \dfrac{1}{6}\overrightarrow b - \dfrac{1}{3}\overrightarrow c + \dfrac{1}{3}\overrightarrow d $
D

$\overrightarrow {MG} = - \dfrac{1}{6}\overrightarrow b - \dfrac{1}{3}\overrightarrow c - \dfrac{1}{3}\overrightarrow d $.

Đáp án : A

Phương pháp giải :

Sử dụng công thức trọng tâm $\overrightarrow {MG} = \dfrac{1}{3}\left( {\overrightarrow {MB} + \overrightarrow {MC} + \overrightarrow {MD} } \right)$ và các quy tắc cộng, trừ véc tơ để biểu diễn

Lời giải chi tiết :

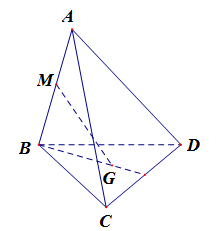$\begin{array}{l}\overrightarrow {MG} = \dfrac{1}{3}\left( {\overrightarrow {MB} + \overrightarrow {MC} + \overrightarrow {MD} } \right) = \dfrac{1}{3}.\dfrac{1}{2}\overrightarrow {AB} + \dfrac{1}{3}\left( {\overrightarrow {MA} + \overrightarrow {AC} } \right) + \dfrac{1}{3}\left( {\overrightarrow {MA} + \overrightarrow {AD} } \right)\\ = \dfrac{1}{6}\overrightarrow {AB} + \dfrac{2}{3}\overrightarrow {MA} + \dfrac{1}{3}\overrightarrow {AC} + \dfrac{1}{3}\overrightarrow {AD} = \dfrac{1}{6}\overrightarrow {AB} + \dfrac{2}{3}.\left( { - \dfrac{1}{2}\overrightarrow {AB} } \right) + \dfrac{1}{3}\overrightarrow {AC} + \dfrac{1}{3}\overrightarrow {AD} \\ = - \dfrac{1}{6}\overrightarrow {AB} + \dfrac{1}{3}\overrightarrow {AC} + \dfrac{1}{3}\overrightarrow {AD} = - \dfrac{1}{6}\overrightarrow b + \dfrac{1}{3}\overrightarrow c + \dfrac{1}{3}\overrightarrow d \end{array}$

Câu 41 :

Cho hình hộp $ABCD.A'B'C'D'$. Giả sử tam giác $AB'C$ và $A'DC'$ đều có 3 góc nhọn. Góc giữa hai đường thẳng $AC$ và $A'D$ là góc nào sau đây?

A

$\widehat {BDB'}$.
B

$\widehat {AB'C}$.
C

$\widehat {DB'B}$.
D

$\widehat {DA'C'}$.

Đáp án : D

Phương pháp giải :

Sử dụng tính chất: $\left\{ \begin{array}{l}a//a'\\b//b'\end{array} \right. \Rightarrow \widehat {\left( {a,b} \right)} = \widehat {\left( {a',b'} \right)}$

Lời giải chi tiết :

Ta có: $AC{\rm{ // }}A'C'$ (tính chất của hình hộp)

$ \Rightarrow \left( {AC,A'D} \right) = \left( {A'C',A'D} \right) = \widehat {DA'C'}$ (do giả thiết cho $\Delta DA'C'$ nhọn).

Câu 42 :

Cho hình chóp $S.ABC$ có $SA = SB = SC$ và tam giác $ABC$ vuông tại $B$. Vẽ $SH \bot \left( {ABC} \right)$, $H \in \left( {ABC} \right)$. Khẳng định nào sau đây đúng?

A

$H$ trùng với trọng tâm tam giác $ABC$.
B

$H$ trùng với trực tâm tam giác $ABC$.
C

$H$ trùng với trung điểm của $AC$.
D

$H$ trùng với trung điểm của $BC$.

Đáp án : C

Phương pháp giải :

Sử dụng tính chất: Điểm $S$ thỏa mãn $SA = SB = SC$ thì $HA = HB = HC$ với $H$ là hình chiếu của $S$ lên mặt phẳng $\left( {ABC} \right)$.

Lời giải chi tiết :

Do $SA = SB = SC$ nên $HA = HB = HC$. Suy ra $H$ là tâm đường tròn ngoại tiếp $\Delta ABC$.

Mà $\Delta ABC$ vuông tại $B$ nên $H$ là trung điểm của $AC$.

Câu 43 :

A

$\left( {IJK} \right){\rm{//}}\left( {SAC} \right)$.
B

$BD \bot \left( {IJK} \right)$.
C

Góc giữa $SC$ và $BD$ có số đo $60^\circ $.
D

$BD \bot \left( {SAC} \right)$.

Đáp án : C

Phương pháp giải :

Sử dụng các cách chứng minh đường thẳng vuông góc mặt phẳng, mặt phẳng song song mặt phẳng để xét tính đúng, sai của các đáp án.

Lời giải chi tiết :

Do $IJ\;{\rm{//}}\;AC$ và $IK{\rm{//}}SA$ nên $\left( {IJK} \right){\rm{//}}\left( {SAC} \right)$. Vậy A đúng.

Do $BD \bot AC$ và $BD \bot SA$ nên $BD \bot \left( {SAC} \right)$ nên D đúng.

Do $BD \bot \left( {SAC} \right)$ và $\left( {IJK} \right){\rm{//}}\left( {SAC} \right)$ nên $BD \bot \left( {IJK} \right)$ nên B đúng.

Vậy C sai.

Câu 44 :

A

$\sin \beta = \dfrac{1}{2}$.
B

$\cot \beta = \dfrac{{\sqrt 3 }}{2}$.
C

$\tan \beta = \dfrac{{\sqrt 3 }}{2}$.
D

$\beta = {60^0}$.

Đáp án : C

Phương pháp giải :

- Xác định góc giữa $SB$ và $\left( {ABCD} \right)$, tính $SO$.

- Xác định góc giữa $SC$ và $\left( {ABCD} \right)$ và tính tỉ số lượng giác của góc đó.

Lời giải chi tiết :

Vì $SO \bot \left( {ABCD} \right)$ nên $OB$ là hình chiếu của $SB$ trên mặt phẳng đáy.

Do đó $\alpha = \left( {SB,\left( {ABCD} \right)} \right) = \left( {SB,OB} \right) = \widehat {SBO}$ và $\beta = \left( {SC,\left( {ABCD} \right)} \right) = \left( {SC,OC} \right) = \widehat {SCO}$.

Hình thoi $ABCD$ có $AC = 2a,\widehat {ADC} = {60^0} \Rightarrow \Delta ADC$ đều $ \Rightarrow AD = 2a$

Tam giác $AOD$ vuông tại $O$ nên $OD = \sqrt {A{D^2} - A{O^2}} = \sqrt {4{a^2} - {a^2}} = a\sqrt 3 \Rightarrow OB = a\sqrt 3 $.

Lại có $\tan \alpha = \dfrac{1}{2} \Rightarrow \dfrac{{SO}}{{OB}} = \dfrac{1}{2} \Rightarrow SO = \dfrac{1}{2}OB = \dfrac{1}{2}.a\sqrt 3 = \dfrac{{a\sqrt 3 }}{2}$.

Vậy $\tan \beta = \tan \widehat {SCO} = \dfrac{{SO}}{{OC}} = \dfrac{{\dfrac{{a\sqrt 3 }}{2}}}{a} = \dfrac{{\sqrt 3 }}{2}$.

Câu 45 :

A

$3183624$
B

$2343625$
C

$2343626$
D

$2343627$

Đáp án : A

Phương pháp giải :

Sử dụng công thức tổng quát của cấp số nhân để tính số hạng thứ ba của dãy.

Lời giải chi tiết :

Theo giả thiết thì mỗi năm số dân của thành phố A tăng $2\% $ nghĩa là dân số năm sau gấp năm trước $1 + 2\% = 1,02$ lần nên số dân theo các năm liên tiếp lập thành cấp số nhân có số hạng đầu ${u_1} = {3.10^6}$ và công bội $q = 1 + 0,02 $

$\Rightarrow {u_n} = {3.10^6}{\left( {1 + 0,02} \right)^n} \Rightarrow {u_3} = {3.10^6}{\left( {1 + 0,02} \right)^3} = 3183624$

Câu 46 :

A

$\dfrac{{{c^2} - A{B^2}}}{{2(1 - \cos \varphi {\rm{)}}}}$
B

$\dfrac{{{c^2} - A{B^2}}}{{2(1 + \cos \varphi {\rm{)}}}}$
C

$\dfrac{{{c^2} + A{B^2}}}{{2(1 - \cos \varphi {\rm{)}}}}$
D

$\dfrac{{{c^2} + A{B^2}}}{{2(1 + \cos \varphi {\rm{)}}}}$

Đáp án : A

Phương pháp giải :

Biến đổi ${\overrightarrow {MN} ^2} = {\left( {\overrightarrow {MA} + \overrightarrow {AB} + \overrightarrow {BN} } \right)^2}$ và đánh giá biểu thức $AM.BN$

Lời giải chi tiết :

Ta có:

$\begin{array}{l}{c^2} = M{N^2} = {\overrightarrow {MN} ^2} = {\left( {\overrightarrow {MA} + \overrightarrow {AB} + \overrightarrow {BN} } \right)^2} \\ = {\overrightarrow {MA} ^2} + {\overrightarrow {AB} ^2} + {\overrightarrow {BN} ^2} + 2\overrightarrow {MA} .\overrightarrow {AB} + 2\overrightarrow {AB} .\overrightarrow {BN} + 2\overrightarrow {MA} .\overrightarrow {BN} \\ = A{M^2} + A{B^2} + B{N^2} + 2.0 + 2.0 + 2\overrightarrow {MA} .\overrightarrow {BN} \\= A{M^2} + A{B^2} + B{N^2} - 2\overrightarrow {AM} .\overrightarrow {BN} \\ = A{B^2} + A{M^2} + B{N^2} - 2AM.BN.\cos \varphi \end{array}$

$ \ge A{B^2} + 2AM.BN - 2AM.BN\cos \varphi $

$ = A{B^2} + 2AM.BN.(1 - \cos \varphi {\rm{)}} $

$\Rightarrow AM.BN \le \dfrac{{{c^2} - A{B^2}}}{{2(1 - \cos \varphi )}}$

Vậy biểu thức $AM.BN$ đạt giá trị lớn nhất bằng $\dfrac{{{c^2} - A{B^2}}}{{2(1 - \cos \varphi )}}$

Câu 47 :

A

$ - \dfrac{{343}}{8}$
B

$\dfrac{{721}}{8}$
C

$ - \dfrac{{721}}{8}$
D

$\dfrac{{343}}{8}$

Đáp án : C

Phương pháp giải :

Đặt $t = {x^2}\,\,\left( {t \ge 0} \right)$, đưa phương trình đã cho về phương trình bậc 2 ẩn $t$.

Tìm điều kiện của $m$ để phương trình bậc hai ẩn $t$ có hai nghiệm dương phân biệt.

Sử dụng tính chất của cấp số cộng ${u_{n - 1}} + {u_{n + 1}} = 2{u_n}$ để suy ra mối quan hệ giữa hai nghiệm của phương trình bậc hai ẩn $t$

Sử dụng định lý Vi-et.

Lời giải chi tiết :

Đặt $t = {x^2}\,\,\left( {t \ge 0} \right)$, khi đó phương trình trở thành ${t^2} - 10t + 2{m^2} + 7m = 0$ (*)

Phương trình đã cho có 4 nghiệm dương phân biệt $ \Leftrightarrow \left\{ \begin{array}{l}\Delta ' > 0\\S > 0\\P > 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}25 - 2{m^2} - 7m > 0\\10 > 0\\2{m^2} + 7m > 0\end{array} \right. \Leftrightarrow 0 < 2{m^2} + 7m < 25$

Với điều kiện trên thì (*) có 2 nghiệm phân biệt dương là ${t_1},{t_2}\,\,\left( {{t_1} < {t_2}} \right)$. Do đó phương trình ban đầu có 4 nghiệm phân biệt được sắp xếp theo thứ tự tăng dần như sau $ - \sqrt {{t_2}} , - \sqrt {{t_1}} ,\sqrt {{t_1}} ,\sqrt {{t_2}} $.

Bốn nghiệm này lập thành cấp số cộng thì $ - \sqrt {{t_1}} + \sqrt {{t_2}} = 2\sqrt {{t_1}} \Leftrightarrow 3\sqrt {{t_1}} = \sqrt {{t_2}} \Leftrightarrow 9{t_1} = {t_2}$

Mà theo định lí Vi-et ta có ${t_1} + {t_2} = 10 \Leftrightarrow 9{t_2} + {t_2} = 10 \Leftrightarrow {t_2} = 1 \Rightarrow {t_1} = 9$

Lại có ${t_1}{t_2} = 2{m^2} + 7m = 9 \Leftrightarrow \left[ \begin{array}{l}m = 1\\m = - \dfrac{9}{2}\end{array} \right.\,\,\left( {tm} \right)$

Do đó ${1^3} + {\left( { - \dfrac{9}{2}} \right)^3} = - \dfrac{{721}}{8}$

Câu 48 :

Giá trị của $B = {\rm{lim}}\dfrac{{\sqrt[{\rm{n}}]{{n!}}}}{{\sqrt {{n^3} + 2n} }}$ bằng:

A

$ + \infty $
B

$ - \infty $
C

$0$
D

$1$

Đáp án : C

Phương pháp giải :

Nếu ${x_n} < {u_n} < {v_n}$ mà $\lim \,\,{x_n} = \lim \,\,{v_n} = a \Rightarrow \lim \,\,{u_n} = a$

Lời giải chi tiết :

Ta có: $n! < {n^n} \Rightarrow \sqrt[n]{{n!}} < \sqrt[n]{{{n^n}}}$

$ \Rightarrow 0 < \dfrac{{\sqrt[{\rm{n}}]{{n!}}}}{{\sqrt {{n^3} + 2n} }} < \dfrac{{\sqrt[{\rm{n}}]{{{n^n}}}}}{{\sqrt {{n^3} + 2n} }} = \dfrac{n}{{\sqrt {{n^3} + 2n} }}$

Mà $\lim 0 = 0\,;\;\,\,\lim \,\dfrac{n}{{\sqrt {{n^3} + 2n} }} $ $= \lim \dfrac{n}{{n\sqrt {n + \frac{2}{n}} }} $ $= \lim \dfrac{1}{{\sqrt {n + \frac{2}{n}} }} = 0$

$ \Rightarrow \lim \dfrac{{\sqrt[n]{{n!}}}}{{\sqrt {{n^3} + 2n} }} = 0 \Rightarrow B = 0.$

Câu 49 :

A

${S_{AMIN}} = \dfrac{{{a^2}\sqrt 6 }}{7}.$
B

${S_{AMIN}} = \dfrac{{12{a^2}\sqrt 6 }}{{35}}.$
C

${S_{AMIN}} = \dfrac{{6{a^2}\sqrt 6 }}{{35}}.$
D

${S_{AMIN}} = \dfrac{{{a^2}\sqrt 6 }}{5}.$

Đáp án : B

Phương pháp giải :

Lời giải chi tiết :

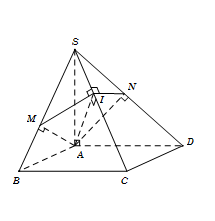Trong tam giác $SAC, $ kẻ $AI \bot SC$ $\left( {\,I \in SC} \right)$

Trong $mp(SBC),$ kẻ ${d_1}$ đi qua $I$ vuông góc với $SC$ cắt $SB $ tại $M.$

Trong $mp(SCD),$ kẻ ${d_2}$ đi qua $I$ vuông góc với $SC$ cắt $SD$ tại $N.$

Khi đó thiết diện của hình chóp cắt bởi mp $\left( \alpha \right)$ là tứ giác $AMIN.$

Ta có $SC \bot \left( \alpha \right) \Rightarrow SC \bot AM$. (1)

Lại có $\left\{ \begin{array}{l}BC \bot AB\\BC \bot SA\end{array} \right. \Rightarrow BC \bot \left( {SAB} \right) \Rightarrow BC \bot AM$. (2)

Từ (1) và (2), suy ra $AM \bot \left( {SBC} \right) \Rightarrow AM \bot MI$. Chứng minh tương tự, ta được $AN \bot NI$.

Do đó ${S_{AMIN}} = {S_{\Delta AMI}} + {S_{\Delta ANI}} $ $= \dfrac{1}{2}AM.MI + \dfrac{1}{2}AN.NI$.

Vì $AM, AI, AN $ là các đường cao của các tam giác vuông $SAB, SAC, SAD $ nên

$AM = \dfrac{{SA.AB}}{{\sqrt {S{A^2} + A{B^2}} }} = \dfrac{{2a}}{{\sqrt 5 }}$; $AI = \dfrac{{SA.AC}}{{\sqrt {S{A^2} + A{C^2}} }} = a\sqrt 2 $; $AN = \dfrac{{SA.AD}}{{\sqrt {S{A^2} + A{D^2}} }} = \dfrac{{2a\sqrt {21} }}{7}$

Suy ra $MI = \sqrt {A{I^2} - A{M^2}} = \dfrac{{a\sqrt {30} }}{5}$ và $NI = \sqrt {A{I^2} - A{N^2}} = \dfrac{{a\sqrt {14} }}{7}$

Vậy ${S_{AMIN}} = \dfrac{1}{2}\left( {\dfrac{{2a}}{{\sqrt 5 }}.\dfrac{{a\sqrt {30} }}{5} + \dfrac{{2a\sqrt {21} }}{7}.\dfrac{{a\sqrt {14} }}{7}} \right) = \dfrac{{12{a^2}\sqrt 6 }}{{35}}$

Câu 50 :

Bất đẳng thức nào sau đây đúng? Với mọi số nguyên dương $n$ thì:

A

$1 + \dfrac{1}{{\sqrt 2 }} + ... + \dfrac{1}{{\sqrt n }} > 2\sqrt n $
B

$1 + \dfrac{1}{{\sqrt 2 }} + ... + \dfrac{1}{{\sqrt n }} > 3\sqrt n $
C

$1 + \dfrac{1}{{\sqrt 2 }} + ... + \dfrac{1}{{\sqrt n }} < 2\sqrt n $
D

$1 + \dfrac{1}{{\sqrt 2 }} + ... + \dfrac{1}{{\sqrt n }} > 4\sqrt 5 $

Đáp án : C

Phương pháp giải :

Thử một giá trị bất kì của $n$ thỏa mãn $n$ là số nguyên dương và dự đoán kết quả.

Chứng minh kết quả vừa dự đoán là đúng bằng phương pháp quy nạp toán học.

Lời giải chi tiết :

Khi $n = 1$ ta có $\dfrac{1}{{\sqrt 1 }} = 1 < 2 \Rightarrow $ Loại đáp án A, B, D.

Ta chứng minh đáp án C đúng bằng phương pháp quy nạp toán học.

Bất đẳng thức đúng với $n = 1$ .

Giả sử bất đẳng thức đúng đến $n = k (k \ge 1)$, tức là

$1 + \dfrac{1}{{\sqrt 2 }} + ... + \dfrac{1}{{\sqrt k }} < 2\sqrt k $ , ta chứng minh bất đẳng thức đúng đến $n = k + 1$ , tức là cần chứng minh $1 + \dfrac{1}{{\sqrt 2 }} + ... + \dfrac{1}{{\sqrt {k + 1} }} < 2\sqrt {k + 1} $

Ta có: $VT = 1 + \dfrac{1}{{\sqrt 2 }} + ... + \dfrac{1}{{\sqrt k }} + \dfrac{1}{{\sqrt {k + 1} }} < 2\sqrt k + \dfrac{1}{{\sqrt {k + 1} }}$

Giả sử:

$2\sqrt k + \dfrac{1}{{\sqrt {k + 1} }} < 2\sqrt {k + 1} $ $\Leftrightarrow \dfrac{1}{{\sqrt {k + 1} }} < 2\sqrt {k + 1} - 2\sqrt k = \dfrac{2}{{\sqrt {k + 1} + \sqrt k }}$ $ \Leftrightarrow \sqrt {k + 1} > \dfrac{{\sqrt {k + 1} }}{2} + \dfrac{{\sqrt k }}{2} $ $\Leftrightarrow \dfrac{{\sqrt {k + 1} }}{2} > \dfrac{{\sqrt k }}{2} \Leftrightarrow \sqrt {k + 1} > \sqrt k $ (luôn đúng)

Do đó

$2\sqrt k + \dfrac{1}{{\sqrt {k + 1} }} < 2\sqrt {k + 1} $ $ \Rightarrow 1 + \dfrac{1}{{\sqrt 2 }} + ... + \dfrac{1}{{\sqrt {k + 1} }} < 2\sqrt {k + 1} $

Do đó bất đẳng thức đúng đến $n = k + 1$.

Vậy $1 + \dfrac{1}{{\sqrt 2 }} + ... + \dfrac{1}{{\sqrt n }} < 2\sqrt n $ đúng với mọi số nguyên dương $n$.

Bài liên quan