Đề thi giữa kì 1 Toán 11 - Đề số 5Đề bài
Câu 1 :
Hàm số \(y = \sin x\) có tập xác định là:
Câu 2 :
Nghiệm của phương trình \(\sin x = - 1\) là:
Câu 3 :
Phương trình \(\sqrt 3 {\cot ^2}x - 4\cot x + \sqrt 3 = 0\) có nghiệm là:
Câu 4 :
Nghiệm của phương trình \(\sin x = \dfrac{1}{2}\) thỏa mãn $ - \dfrac{\pi }{2} \le x \le \dfrac{\pi }{2}$ là:
Câu 5 :
Nghiệm của phương trình \(\sin x.\cos x = 0\) là:
Câu 6 :
Nghiệm của phương trình \(4{\sin ^2}2x + 8{\cos ^2}x - 9 = 0\) là:
Câu 7 :
Đường cong trong hình có thể là đồ thị của hàm số nào dưới đây? 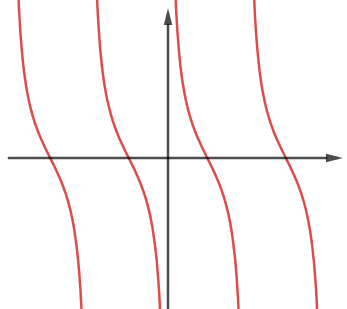
Câu 8 :
Với giá trị nào của m thì phương trình \(\sqrt 3 \sin 2x - m\cos 2x = 1\) luôn có nghiệm?
Câu 9 :
Nghiệm của phương trình \(2\cos x - 1 = 0\) là:
Câu 10 :
Phương trình \(6{\sin ^2}x + 7\sqrt 3 \sin 2x - 8{\cos ^2}x = 6\) có nghiệm là:
Câu 11 :
Trong khoảng \(\left( {0\,\,;\,\,\dfrac{\pi }{2}} \right)\) phương trình \({\sin ^2}4x + 3\sin 4x\cos 4x - 4{\cos ^2}4x = 0\) có:
Câu 12 :
Tìm chu kì của các hàm số sau \(y = \sin \sqrt x \)
Câu 13 :
Phương trình \(\tan \left( {\dfrac{\pi }{2} - x} \right) + 2\tan \left( {2x + \dfrac{\pi }{2}} \right) = 1\) có nghiệm là:
Câu 14 :
Trong mặt phẳng tọa độ $Oxy$ cho đồ thị của hàm số \(y = \sin x\). Có bao nhiêu phép tịnh tiến biến đồ thị đó thành chính nó
Câu 15 :
Cho đường tròn $\left( {O;R} \right)$ và hai điểm $A,B$ phân biệt. Một điểm $M$ thay đổi trên đường tròn $\left( O \right)$. Khi đó tập hợp các điểm $N$ sao cho $\overrightarrow {MN} + \overrightarrow {MA} = \overrightarrow {MB} $ là tập nào sau đây?
Câu 16 :
Ảnh $A'$ của $A\left( {4; - 3} \right)$ qua phép đối xứng trục $d$ với \(d:2x\; - y = 0\) có tọa độ là:
Câu 17 :
Cho hai khẳng định sau: (I) Nếu một hình nào đó có hai trục đối xứng vuông góc với nhau thì hình đó có tâm đối xứng. (II) Cho phép đối xứng tâm ${D_O}$ và đường thẳng $d$ không đi qua $O$. Có thể dựng $d'$ là ảnh của $d$ qua ${D_O}$ mà chỉ sử dụng compa một lần và thước hai lần. Chọn kết luận đúng:
Câu 18 :
Cho hình vuông tâm $O$. Hỏi có bao nhiêu phép quay tâm $O$, góc quay \(\alpha \,\,\left( {0 < \alpha \le 360^0} \right)\) biến hình vuông đã cho thành chính nó.
Câu 19 :
Cho hai đường thẳng song song $d,d'$. Có bao nhiêu phép vị tự tỉ số $k = 5$ biến $d$ thành $d'$ .
Câu 20 :
Phép vị tự nào sau đây biến đường tròn \(\left( C \right):\,\,{\left( {x - 3} \right)^2} + {\left( {y - 1} \right)^2} = 4\) thành đường tròn \(\left( {C'} \right):\,\,{\left( {x - 5} \right)^2} + {\left( {y - 3} \right)^2} = 4\) ?
Câu 21 :
Xét sự biến thiên của hàm số \(y = \sin x - \cos x\). Trong các kết luận sau, kết luận nào đúng?
Câu 22 :
Phương trình \(\cos 11x\cos 3x = \cos 17x\cos 9x\) có nghiệm là:
Câu 23 :
Phương trình \(\cot 20x = 1\) có bao nhiêu nghiệm thuộc khoảng \(\left[ { - 50\pi ;0} \right]\)?
Câu 24 :
Giải phương trình \(\cos 3x\tan 5x = \sin 7x\).
Câu 25 :
Cho đường tròn \(\left( {O;R} \right)\) đường kính \(AB\). Điểm \(M\) nằm trên \(AB\). Qua \(AB\) kẻ dây \(CD\) tạo với \(AB\) một góc \({45^0}\). Gọi \(D'\) là điểm đối xứng của \(D\) qua \(AB\). Tính \(M{C^2} + MD{'^2}\) theo \(R\)?
Lời giải và đáp án
Câu 1 :
Hàm số \(y = \sin x\) có tập xác định là:
Đáp án : D Lời giải chi tiết :
Hàm \(y = \sin x\) có TXĐ \(D = R\). Chú ý
Một số em có thể sẽ nhầm với điều kiện xác định của hàm \(y = \tan x\) hoặc \(y = \cot x\) và chọn nhầm đáp án sai.
Câu 2 :
Nghiệm của phương trình \(\sin x = - 1\) là:
Đáp án : C Lời giải chi tiết :
Ta có: \(\sin x = - 1 \Leftrightarrow \sin x = \sin \left( { - \dfrac{\pi }{2}} \right) \Leftrightarrow x = - \dfrac{\pi }{2} + k2\pi \left( {k \in Z} \right)\) Chú ý
Một số em có thể sẽ chọn nhầm đáp án D vì nhầm với phương trình \(\cos x = - 1\) là sai.
Câu 3 :
Phương trình \(\sqrt 3 {\cot ^2}x - 4\cot x + \sqrt 3 = 0\) có nghiệm là:
Đáp án : A Phương pháp giải :
- Tìm ĐKXĐ của phương trình. - Đặt \(\cot x = t\) và giải phương trình tìm \(t\), từ đó tìm \(x\). Lời giải chi tiết :
ĐK: \(\sin x \ne 0 \Leftrightarrow x \ne k\pi \,\,\left( {k \in Z} \right)\) \(\sqrt 3 {\cot ^2}x - 4\cot x + \sqrt 3 = 0\) Đặt \(\cot x = t\) khi đó phương trình có dạng $\sqrt 3 {t^2} - 4t + \sqrt 3 = 0 \Leftrightarrow \left[ \begin{array}{l}t = \dfrac{1}{{\sqrt 3 }}\\t = \sqrt 3 \end{array} \right. \Rightarrow \left[ \begin{array}{l}\cot x = \dfrac{1}{{\sqrt 3 }}\\\cot x = \sqrt 3 \end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = \dfrac{\pi }{3} + k\pi \\x = \dfrac{\pi }{6} + k\pi \end{array} \right.\,\,\left( {k \in Z} \right)\,\,\left( {tm} \right)$
Câu 4 :
Nghiệm của phương trình \(\sin x = \dfrac{1}{2}\) thỏa mãn $ - \dfrac{\pi }{2} \le x \le \dfrac{\pi }{2}$ là:
Đáp án : B Phương pháp giải :
Bước 1: Đưa $\dfrac{1}{2}$ về dạng $\sin \alpha $ Sử dụng máy tính để tìm $\alpha $: SHIFT => MODE => 4 : chuyển về chế độ Radian SHIFT => SIN => (1/2) =>"="
Bước 2: Giải phương trình lượng giác cơ bản \(\sin x = \sin \alpha \Leftrightarrow \left[ \begin{array}{l}x = \alpha + k2\pi \\x = \pi - \alpha + k2\pi \end{array} \right.\) Bước 3: Xét từng họ nghiệm và thay vào $ - \dfrac{\pi }{2} \le x \le \dfrac{\pi }{2}$ để tìm k sau đó thay k ngược lại để tìm x. Lời giải chi tiết :
Bước 1: Ta có: \(\sin x = \dfrac{1}{2} \Leftrightarrow \sin x = \sin \dfrac{\pi }{6}\) Bước 2: \( \Leftrightarrow \left[ \begin{array}{l}x = \dfrac{\pi }{6} + k2\pi \\x = \dfrac{{5\pi }}{6} + k2\pi \end{array} \right.\left( {k \in Z} \right)\) Bước 3: +) Xét $x = \dfrac{\pi }{6} + k2\pi$ Ta có $ - \dfrac{\pi }{2} \le x \le \dfrac{\pi }{2} \Leftrightarrow - \dfrac{\pi }{2} \le \dfrac{\pi }{6} + k2\pi \le \dfrac{\pi }{2} $ \(\begin{array}{l} - \dfrac{{2\pi }}{3} \le k2\pi \le \dfrac{\pi }{3} \Leftrightarrow - \dfrac{{2\pi }}{{3.2\pi }} \le k \le \dfrac{\pi }{{3.2\pi }}\\ \Leftrightarrow - \dfrac{1}{3} \le k \le \dfrac{1}{6}\end{array}\) Mà \(k \in \mathbb{Z} \Rightarrow k = 0\). Thay vào x ta được: \(x = \dfrac{\pi }{6}\) +) Xét \(x = \dfrac{{5\pi }}{6} + k2\pi \) \(\begin{array}{l} - \dfrac{\pi }{2} \le x \le \dfrac{\pi }{2} \Leftrightarrow - \dfrac{\pi }{2} \le \dfrac{{5\pi }}{6} + k2\pi \le \dfrac{\pi }{2}\\ \Leftrightarrow - \dfrac{{4\pi }}{3} \le k2\pi \le - \dfrac{\pi }{3} \Leftrightarrow - \dfrac{{4\pi }}{{3.2\pi }} \le k \le - \dfrac{\pi }{{3.2\pi }}\\ \Leftrightarrow - \dfrac{2}{3} \le k \le - \dfrac{1}{6}\end{array}\) Mà \(k \in \mathbb{Z}\) nên không có giá trị k thỏa mãn Vậy phương trình ban đầu có nghiệm duy nhất là \(x = \dfrac{\pi }{6}\) Chú ý
Một số em có thể sẽ chọn nhầm đáp án D vì giải sai phương trình lượng giác. Hoặc một số em khác sẽ chọn nhầm đáp án C vì quên mất điều kiện $ - \dfrac{\pi }{2} \le x \le \dfrac{\pi }{2}$.
Câu 5 :
Nghiệm của phương trình \(\sin x.\cos x = 0\) là:
Đáp án : B Phương pháp giải :
Bước 1: Sử dụng công thức nhân đôi $2\sin x. \cos x =\sin 2x$ đưa về phương trình lượng giác cơ bản đối với \(\sin 2x\). Bước 2: Sử dụng công thức $\sin x=0 \Leftrightarrow x=k\pi$
Lời giải chi tiết :
Bước 1: \(\sin x.\cos x = 0 \Leftrightarrow \dfrac{1}{2}\sin 2x = 0\) Bước 2: \( \Leftrightarrow \sin 2x = 0 \Leftrightarrow 2x = k\pi \) \( \Leftrightarrow x = \dfrac{{k\pi }}{2}\left( {k \in \mathbb{Z}} \right)\)
Câu 6 :
Nghiệm của phương trình \(4{\sin ^2}2x + 8{\cos ^2}x - 9 = 0\) là:
Đáp án : A Phương pháp giải :
Bước 1: Sử dụng các công thức biến đổi lượng giác để biến đổi phương trình thành phương trình bậc hai đối với \(\cos 2x\). Các công thức: \({\sin ^2}x + {\cos ^2}x = 1\) ${\cos ^2}x =\dfrac{{1 + \cos 2x}}{2} $ Bước 2: Đặt \(t = \cos 2x\left( { - 1 \le t \le t} \right)\), giải phương trình ẩn \(t\) rồi giải phương trình tìm \(x\). $\cos x= \cos a \Leftrightarrow x=\pm a+ k2\pi$ Lời giải chi tiết :
Bước 1: \(\begin{array}{l}4{\sin ^2}2x + 8{\cos ^2}x - 9 = 0\\ \Leftrightarrow 4\left( {1 - {{\cos }^2}2x} \right) + 8.\dfrac{{1 + \cos 2x}}{2} - 9 = 0\\ \Leftrightarrow 4\left( {1 - {{\cos }^2}2x} \right) + 4\left( {1 + \cos 2x} \right) - 9 = 0\\\Leftrightarrow 4\left( {1 - {{\cos }^2}2x} \right) + 4 + 4\cos 2x - 9 = 0\\ \Leftrightarrow 4 - 4{\cos ^2}2x + 4\cos 2x - 5 = 0 \\\Leftrightarrow - 4{\cos ^2}2x + 4\cos 2x - 1 = 0\end{array}\) Bước 2: Đặt \(\cos 2x = t\,\,\left( { - 1 \le t \le 1} \right)\) khi đó phương trình có dạng \( - 4{t^2} + 4t - 1 = 0 \)\( \Leftrightarrow - \left( {4{t^2} - 4t + 1} \right) = 0\)\(\Leftrightarrow - {\left( {2t - 1} \right)^2} = 0 \) \(\Leftrightarrow t = \dfrac{1}{2}\left( {tm} \right)\) \(\begin{array}{l} \Leftrightarrow \cos 2x = \dfrac{1}{2} \Leftrightarrow \cos 2x =\cos \dfrac{\pi }{3} \\\Leftrightarrow 2x = \pm \dfrac{\pi }{3} + k2\pi \Leftrightarrow x = \pm \dfrac{\pi }{6} + k\pi \left( {k \in Z} \right)\end{array}\)
Câu 7 :
Đường cong trong hình có thể là đồ thị của hàm số nào dưới đây? 
Đáp án : A Lời giải chi tiết :
Nhận xét: Hàm số \(y = \sin x\) và \(y = \cos x\) có đồ thị hình sin nên loại. Đường cong trên từng đoạn có hướng đi xuống nên hàm số nghịch biến trên mỗi đoạn đó. Trong các đáp án đã cho thì chỉ có hàm số \(y = \cot x\) có dạng đồ thị như trên. Chú ý
Một số em có thể sẽ nhầm với đồ thị hàm số \(y = \tan x\) và chọn nhầm đáp án B là sai.
Câu 8 :
Với giá trị nào của m thì phương trình \(\sqrt 3 \sin 2x - m\cos 2x = 1\) luôn có nghiệm?
Đáp án : D Phương pháp giải :
Điều kiện để phương trình \(a\cos x + b\sin x = c\) có nghiệm là \({a^2} + {b^2} \ge {c^2}\) Lời giải chi tiết :
\(\sqrt 3 \sin 2x - m\cos 2x = 1\) Ta có: \(\left\{ \begin{array}{l}a = \sqrt 3 \\b = - m\\c = 1\end{array} \right.\) Để phương trình có nghiệm thì \({a^2} + {b^2} \ge {c^2} \Leftrightarrow 3 + {m^2} \ge 1 \Leftrightarrow {m^2} \ge - 2\) (luôn đúng với \(\forall m\) ) Vậy phương trình luôn có nghiệm với mọi $m$.
Câu 9 :
Nghiệm của phương trình \(2\cos x - 1 = 0\) là:
Đáp án : D Lời giải chi tiết :
Ta có: \(2\cos x - 1 = 0 \Leftrightarrow \cos x = \dfrac{1}{2} \Leftrightarrow \cos x = \cos \dfrac{\pi }{3} \Leftrightarrow x = \pm \dfrac{\pi }{3} + k2\pi \left( {k \in Z} \right)\) Chú ý
Một số em có thể sẽ chọn nhầm đáp án B vì xác định nhầm \(\cos \dfrac{\pi }{6} = \dfrac{1}{2}\) là sai.
Câu 10 :
Phương trình \(6{\sin ^2}x + 7\sqrt 3 \sin 2x - 8{\cos ^2}x = 6\) có nghiệm là:
Đáp án : A Phương pháp giải :
- Xét \(\cos x = 0\) có thỏa mãn phương trình hay không. - Xét \(\cos x \ne 0\) thì chia cả hai vế của phương trình cho \({\cos ^2}x \ne 0\), trở thành phương trình bậc hai với ẩn là \(\tan x\) - Giải phương trình trên tìm \(\tan x\) suy ra nghiệm \(x\). Lời giải chi tiết :
\(6{\sin ^2}x + 7\sqrt 3 \sin 2x - 8{\cos ^2}x = 6 \Leftrightarrow 6{\sin ^2}x + 14\sqrt 3 \sin x\cos x - 8{\cos ^2}x = 6\,\left( * \right)\) Trường hợp 1: \(\cos x = 0 \Leftrightarrow x = \dfrac{\pi }{2} + k\pi \left( {k \in Z} \right)\). Khi đó \({\sin ^2}x = 1\) Thay vào phương trình (*) ta có: \(6.1 + 14.0 - 8.0 = 6 \Leftrightarrow 6 = 6\) (luôn đúng) \( \Rightarrow x = \dfrac{\pi }{2} + k\pi \left( {k \in Z} \right)\)là nghiệm của phương trình. Trường hợp 2: \(\cos x \ne 0 \Leftrightarrow x \ne \dfrac{\pi }{2} + k\pi \left( {k \in Z} \right)\). Chia cả 2 vế của phương trình (*) cho \({\cos ^2}x\) ta được: \(\begin{array}{l}6\dfrac{{{{\sin }^2}x}}{{{{\cos }^2}x}} + 14\sqrt 3 \dfrac{{\sin x}}{{\cos x}} - 8 = \dfrac{6}{{{{\cos }^2}x}} \Leftrightarrow 6{\tan ^2}x + 14\sqrt 3 \tan x - 8 = 6\left( {1 + {{\tan }^2}x} \right)\\ \Leftrightarrow 14\sqrt 3 \tan x - 14 = 0 \Leftrightarrow \sqrt 3 {\mathop{\rm tanx}\nolimits} - 1 = 0 \Leftrightarrow \tan x = \dfrac{1}{{\sqrt 3 }} \Leftrightarrow x = \dfrac{\pi }{6} + k\pi \left( {k \in Z} \right)\end{array}\) Kết hợp 2 trường hợp ta có nghiệm của phương trình là: \(\left[ \begin{array}{l}x = \dfrac{\pi }{2} + k\pi \\x = \dfrac{\pi }{6} + k\pi \end{array} \right.\left( {k \in Z} \right)\)
Câu 11 :
Trong khoảng \(\left( {0\,\,;\,\,\dfrac{\pi }{2}} \right)\) phương trình \({\sin ^2}4x + 3\sin 4x\cos 4x - 4{\cos ^2}4x = 0\) có:
Đáp án : D Phương pháp giải :
- Xét \(\cos 4x = 0\) có thỏa mãn phương trình hay không. - Xét \(\cos 4x \ne 0\), chia cả hai vế phương trình cho \({\cos ^2}4x \ne 0\), giải phương trình bậc hai ẩn \(\tan x\), từ đó suy ra nghiệm của phương trình. Lời giải chi tiết :
Trường hợp 1: \(\cos 4x = 0 \Leftrightarrow 4x = \dfrac{\pi }{2} + k\pi \Leftrightarrow x = \dfrac{\pi }{8} + \dfrac{{k\pi }}{4}\,\,\left( {k \in Z} \right)\). Khi đó \({\sin ^2}4x = 1\)
Câu 12 :
Tìm chu kì của các hàm số sau \(y = \sin \sqrt x \)
Đáp án : A Phương pháp giải :
Tìm tập xác định \(D\) của hàm số. Kiểm tra điều kiện \(\left\{ \begin{array}{l} Lời giải chi tiết :
TXĐ: \(D = \left[ {0; + \infty } \right)\). Thay lần lượt các đáp án B, C, D vào \(x - T\), nếu \(\exists x \in D:x - T \notin D \) hoặc \(\exists x \in D:x +T \notin D \) thì đáp án không thỏa mãn. Chẳng hạn, ta thử đáp án B: \(T = 2\pi \). Với \(x = 0 \Rightarrow x - T = - 2\pi \notin D \Rightarrow \) \(\exists x \in D:x - T \notin D \forall T > 0\). Vậy hàm số không tuần hoàn. Chú ý
Một số em có thể sẽ chọn nhầm đáp án D vì nghĩ \(\sqrt {4{\pi ^2}} = 2\pi \) nên \(\sin \left( {\sqrt {x + 4{\pi ^2}} } \right) = \sin \sqrt x \) là sai. Một số em khác lại biến đổi \(\sin \left( {\sqrt x + 2\pi } \right) = \sin \sqrt x \) và kết luận \(T = 2\pi \) là chu kì là sai vì định nghĩa chu kì \(f\left( {x + T} \right) = f\left( x \right)\).
Câu 13 :
Phương trình \(\tan \left( {\dfrac{\pi }{2} - x} \right) + 2\tan \left( {2x + \dfrac{\pi }{2}} \right) = 1\) có nghiệm là:
Đáp án : B Phương pháp giải :
Bước 1: Sử dụng giá trị lượng giác của các góc hơn kém nhau một góc \(\dfrac{\pi }{2}\) $\tan \left( {\dfrac{\pi }{2} - x} \right) =\cot x$; $\tan \left( {2x + \dfrac{\pi }{2}} \right) =-\cot 2x$ Bước 2: Biến đổi phương trình và giải +) Công thức nhân đôi \(\cot 2x = \dfrac{{1 - {{\tan }^2}x}}{{2\tan x}}\). +) Sử dụng công thức $\tan x = \tan y \Leftrightarrow x = y+ k\pi \left( {k \in Z} \right)$ Lời giải chi tiết :
Bước 1: Ta có: \(\tan \left( {\dfrac{\pi }{2} - x} \right) + 2\tan \left( {2x + \dfrac{\pi }{2}} \right) = 1 \)\(\Leftrightarrow \cot x - 2\cot 2x = 1\) ĐK: \(\left\{ \begin{array}{l}\sin x \ne 0\\\sin 2x \ne 0\end{array} \right. \Leftrightarrow \sin 2x \ne 0 \Leftrightarrow x \ne \dfrac{{k\pi }}{2}\) Bước 2: Khi đó phương trình tương đương: \(\begin{array}{l}\cot x - 2\cot 2x = 1 \\ \Leftrightarrow \cot x - 2.\dfrac{{1 - {{\tan }^2}x}}{{2\tan x}} = 1 \\ \Leftrightarrow \cot x - \dfrac{{\tan x.\cot x - {{\tan }^2}x}}{{\tan x}} = 1\\ \Leftrightarrow \cot x - \left( {\cot x - \tan x} \right) = 1 \Leftrightarrow \tan x = 1 \Leftrightarrow x = \dfrac{\pi }{4} + k\pi \left( {k \in Z} \right)\left( {TMDK} \right)\end{array}\) Chú ý
Cần vận dụng linh hoạt các công thức biến đổi lượng giác để áp dụng vào bài toán. Một số em khi biến đổi \(\cot x - \left( {\cot x - \tan x} \right) = 1 \Leftrightarrow - \tan x = 1 \Leftrightarrow \tan x = - 1\) và chọn nhầm đáp án D là sai.
Câu 14 :
Trong mặt phẳng tọa độ $Oxy$ cho đồ thị của hàm số \(y = \sin x\). Có bao nhiêu phép tịnh tiến biến đồ thị đó thành chính nó
Đáp án : D Phương pháp giải :
Sử dụng biểu thức tọa độ của phép tịnh tiến \(\left\{ \begin{array}{l}x' = x + a\\y' = y + b\end{array} \right.\). $\sin a=0 \Leftrightarrow a=k\pi$ $\cos a =1\Leftrightarrow a=k2\pi$ Lời giải chi tiết :
Cách 1: Ta có: \(y = \sin x = \sin \left( {x + k2\pi } \right) \Rightarrow \left\{ \begin{array}{l}x' = x + k2\pi \\y' = y\end{array} \right. \Rightarrow \overrightarrow u = \left( {k2\pi ;0} \right)\) Do \(k \in Z\) nên có vô số véc tơ \(\overrightarrow u \) như trên. Cách 2: Gọi vectơ tịnh tiến là \(\overrightarrow v = \left( {a;b} \right)\). Ta có: \(\left\{ \begin{array}{l} Do \(y = \sin x\) nên \(y' - b = \sin \left( {x' - a} \right)\) \( \Leftrightarrow y' = \sin \left( {x' - a} \right) + b\). Để \(\overrightarrow v \) biến đồ thị thành chính nó thì \(y' = \sin x'\) \(\forall x'\) \( \Leftrightarrow \sin x' = \sin \left( {x' - a} \right) + b\) \(\forall x'\). Với \(x = 0 \Rightarrow 0 = - \sin a + b \Leftrightarrow \sin a = b\). Với \(x = \pi \Rightarrow 0 = \sin a + b \Leftrightarrow \sin a = - b\). Với \(x = \dfrac{\pi }{2} \Rightarrow 1 = \cos a + b \Leftrightarrow \cos a = 1 - b\). Từ đó, ta có: \( b = 0;a = k2\pi \) Chú ý
Một số em có thể sẽ chọn nhầm đáp án B vì chỉ xác định được một véc tơ \(\overrightarrow u = \left( {2\pi ;0} \right)\) là sai.
Câu 15 :
Cho đường tròn $\left( {O;R} \right)$ và hai điểm $A,B$ phân biệt. Một điểm $M$ thay đổi trên đường tròn $\left( O \right)$. Khi đó tập hợp các điểm $N$ sao cho $\overrightarrow {MN} + \overrightarrow {MA} = \overrightarrow {MB} $ là tập nào sau đây?
Đáp án : D Phương pháp giải :
- Biến đổi $\overrightarrow {MN} + \overrightarrow {MA} = \overrightarrow {MB} \Leftrightarrow \overrightarrow {MN} = \overrightarrow {AB} $. - Sử dụng tính chất: Phép tịnh tiến biến đường tròn thành đường tròn bằng nó. Lời giải chi tiết :
Từ giả thiết ta có: $\overrightarrow {MN} + \overrightarrow {MA} = \overrightarrow {MB} \Leftrightarrow \overrightarrow {MN} = \overrightarrow {MB} - \overrightarrow {MA} \Leftrightarrow \overrightarrow {MN} = \overrightarrow {AB} $ Như thế phép tịnh tiến theo vectơ $\overrightarrow u = \overrightarrow {AB} $ biến điểm $M$ thành điểm $N$. Vậy khi $M$ thay đổi trên đường tròn $\left( {O;R} \right)$ thì quỹ tích của $N$ là đường tròn $\left( {I;R} \right)$ với $\overrightarrow {OI} = \overrightarrow {AB} $. 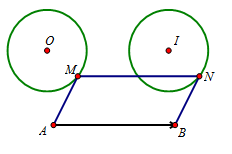 Chú ý
Một số em có thể sẽ chọn nhầm đáp án B vì nghĩ rằng $\overrightarrow{MN}=\overrightarrow{AB}$ nên \(N\) nằm trên đường tròn tâm \(A\) bán kính \(AB\) là sai
Câu 16 :
Ảnh $A'$ của $A\left( {4; - 3} \right)$ qua phép đối xứng trục $d$ với \(d:2x\; - y = 0\) có tọa độ là:
Đáp án : B Phương pháp giải :
- Viết phương trình đường thẳng $d’$ qua $A$ và vuông góc với $d.$ - Tìm giao điểm $H$ của $d$ và $d’.$ Khi đó $H$ là trung điểm của $AA’.$ Áp dụng công thức tìm tọa độ trung điểm \(\left\{ \begin{array}{l}{x_A} + {x_{A'}} = 2{x_H}\\{y_A} + {y_{A'}} = 2{y_H}\end{array} \right.\) Lời giải chi tiết :
Gọi \(A'\) là ảnh của $A$ qua phép đối xứng trục $d.$ Gọi $d’$ là đường thẳng đi qua $A $ và vuông góc với $d,$ khi đó phương trình $d’$ có dạng: $x + 2y + c = 0.$ Vì \(A \in d'\) nên \(4 + 2\left( { - 3} \right) + c = 0 \Rightarrow c = 2\). Khi đó \(\left( {d'} \right):x + 2y + 2 = 0\) Gọi \(H = d \cap d' \Rightarrow H\left( { - \dfrac{2}{5}; - \dfrac{4}{5}} \right) \Rightarrow \) $H $ là trung điểm của $AA’.$ Khi đó \(\left\{ \begin{array}{l}{x_{A'}} = 2{x_H} - {x_A}\\{y_{A'}} = 2{y_H} - {y_A}\end{array} \right. \Rightarrow \left\{ \begin{array}{l}{x_{A'}} = 2.\left( { - \dfrac{2}{5}} \right) - 4 = - \dfrac{{24}}{5}\\{y_{A'}} = 2\left( { - \dfrac{4}{5}} \right) + 3 = \dfrac{7}{5}\end{array} \right. \Rightarrow A'\left( { - \dfrac{{24}}{5};\dfrac{7}{5}} \right)\)
Câu 17 :
Cho hai khẳng định sau: (I) Nếu một hình nào đó có hai trục đối xứng vuông góc với nhau thì hình đó có tâm đối xứng. (II) Cho phép đối xứng tâm ${D_O}$ và đường thẳng $d$ không đi qua $O$. Có thể dựng $d'$ là ảnh của $d$ qua ${D_O}$ mà chỉ sử dụng compa một lần và thước hai lần. Chọn kết luận đúng:
Đáp án : C Phương pháp giải :
Suy luận từng đáp án. Lời giải chi tiết :
(I) đúng, tâm đối xứng của hình đó chính là giao điểm của hai trục đối xứng. (II) Cách dựng đường thẳng $d'$ là ảnh của $d$ qua phép đối xứng tâm $O$. Bước 1: Lấy một điểm $M$ bất kì thuộc $d$ Bước 2: Vẽ đường tròn tâm $O$ bán kính $OM$. Bước 3: Kéo dài $OM$, cắt đường tròn tâm $O$ bán kính $OM$ tại điểm thứ hai $N$ . Bước 4: Qua $N$ kẻ đường thẳng song song với $d$. Vậy ta cần dùng compa ở bước 2 và dùng thước ở bước 3 và 4. Do đó cả (I) và (II) đều đúng.
Câu 18 :
Cho hình vuông tâm $O$. Hỏi có bao nhiêu phép quay tâm $O$, góc quay \(\alpha \,\,\left( {0 < \alpha \le 360^0} \right)\) biến hình vuông đã cho thành chính nó.
Đáp án : D Phương pháp giải :
Sử dụng tính chất của hình vuông để xác định các góc quay thỏa mãn bài toán. Lời giải chi tiết :
$\begin{array}{l} Vậy có 4 phép quay cần tìm. 
Câu 19 :
Cho hai đường thẳng song song $d,d'$. Có bao nhiêu phép vị tự tỉ số $k = 5$ biến $d$ thành $d'$ .
Đáp án : D Lời giải chi tiết :
 Có vô số phép vị tự tâm không thuộc $d$ với tỉ số $k = 5$ biến đường thẳng $d$ thành $d’$
Câu 20 :
Phép vị tự nào sau đây biến đường tròn \(\left( C \right):\,\,{\left( {x - 3} \right)^2} + {\left( {y - 1} \right)^2} = 4\) thành đường tròn \(\left( {C'} \right):\,\,{\left( {x - 5} \right)^2} + {\left( {y - 3} \right)^2} = 4\) ?
Đáp án : A Phương pháp giải :
Gọi phép vị tự cần tìm là \({V_{\left( {I;k} \right)}}\), có \(\left| k \right| = \dfrac{{R'}}{R}\) Gọi $K$ và $K'$ lần lượt là tâm của đường tròn \(\left( C \right)\) và đường tròn \(\left( {C'} \right)\) ta có \(\overrightarrow {IK'} = k\overrightarrow {IK} \) Lời giải chi tiết :
Đường tròn \(\left( C \right)\) có tâm \(K\left( {3;1} \right)\) và bán kính \(R = 2\), đường tròn \(\left( {C'} \right)\) có tâm \(K'\left( {5;3} \right)\) và bán kính \(R' = 2\). \( \Rightarrow \left| k \right| = \dfrac{{R'}}{R} = 1 \Rightarrow k = \pm 1\), mà \(I' \ne I \Rightarrow k \ne 1 \Rightarrow k = - 1\) Giả sử phép vị tự tâm $I$ tỉ số $k$ biến $K$ thành $K'$ ta có: \(\overrightarrow {IK'} = - \overrightarrow {IK} \Rightarrow I\) là trung điểm của \(KK' \Rightarrow I\left( {4;2} \right)\)
Câu 21 :
Xét sự biến thiên của hàm số \(y = \sin x - \cos x\). Trong các kết luận sau, kết luận nào đúng?
Đáp án : A Phương pháp giải :
- Biến đổi: \(\sin x - \cos x = \sqrt 2 \sin \left( {x - \dfrac{\pi }{4}} \right)\). - Xác định chu kì tuần hoàn của hàm số và suy ra các khoảng đơn điệu của hàm số. - Hàm số \(y = \sin x\) đồng (nghịch) biến trên \(\left( {a;b} \right)\) thì hàm số \(y = \sin \left( {x - k} \right)\) đồng (nghịch) biến trên khoảng \(\left( {a + k;b + k} \right)\). Lời giải chi tiết :
Ta có: \(\sin x - \cos x = \sqrt 2 \sin \left( {x - \frac{\pi }{4}} \right)\) nên tập giá trị của hàm số là \(\left[ { - \sqrt 2 ;\sqrt 2 } \right]\), do đó loại đáp án C. Hàm số đã cho tuần hoàn với chu kì \(2\pi \), ta xét sự biến thiên của hàm số trên đoạn \(\left[ { - \dfrac{\pi }{4};\dfrac{{7\pi }}{4}} \right]\). - Hàm số \(y = \sin x\) đồng biến trên \(\left( { - \dfrac{\pi }{2};\dfrac{\pi }{2}} \right)\) nên hàm số \(y = \sqrt 2 \sin \left( {x - \dfrac{\pi }{4}} \right)\) nghịch biến trên \(\left( { - \dfrac{\pi }{4};\dfrac{{3\pi }}{4}} \right)\). - Hàm số \(y = \sin x\) nghịch biến trên \(\left( {\dfrac{\pi }{2};\dfrac{{3\pi }}{2}} \right)\) nên hàm số \(y = \sqrt 2 \sin \left( {x - \dfrac{\pi }{4}} \right)\) nghịch biến trên \(\left( {\dfrac{{3\pi }}{4};\dfrac{{7\pi }}{4}} \right)\).
Câu 22 :
Phương trình \(\cos 11x\cos 3x = \cos 17x\cos 9x\) có nghiệm là:
Đáp án : B Phương pháp giải :
Bước 1: Sử dụng công thức biến đổi tích thành tổng: \(\cos a\cos b = \dfrac{1}{2}\left[ {\cos \left( {a + b} \right) + \cos \left( {a - b} \right)} \right]\) để đưa về phương trình lượng giác cơ bản. Bước 2: Giải phương trình lượng giác cơ bản: \(\cos x = \cos \alpha \Leftrightarrow x = \pm \alpha + k2\pi \,\,\left( {k \in \mathbb{Z}} \right)\). Lời giải chi tiết :
Bước 1: $\cos 11x\cos 3x = \cos 17x\cos 9x$ \( \Leftrightarrow \dfrac{1}{2}.\left[ {\cos \left( {11x + 3x} \right) + \cos \left( {11x - 3x} \right)} \right]\)\( = \dfrac{1}{2}\left[ {\cos \left( {17x + 9x} \right) + \cos \left( {17x - 9x} \right)} \right]\) $\Leftrightarrow \dfrac{1}{2}\left( {\cos 14x + \cos 8x} \right) = \dfrac{1}{2}\left( {\cos 26x + \cos 8x} \right)\\ \Leftrightarrow \cos 14x + \cos 8x = \cos 26x + \cos 8x\\ \Leftrightarrow \cos 14x = \cos 26x$ Bước 2: \(\begin{array}{l} \Leftrightarrow \left[ \begin{array}{l}26x = 14x + k2\pi \\26x = - 14x + k2\pi \end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l}12x = k2\pi \\40x = k2\pi \end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l}x = \dfrac{{k\pi }}{6}\\x = \dfrac{{k\pi }}{{20}}\end{array} \right.\,\,\,\left( {k \in \mathbb{Z}} \right)\end{array}\) Vậy nghiệm của phương trình là \(x = \dfrac{{k\pi }}{6},\,\,x = \dfrac{{k\pi }}{{20}}\).
Câu 23 :
Phương trình \(\cot 20x = 1\) có bao nhiêu nghiệm thuộc khoảng \(\left[ { - 50\pi ;0} \right]\)?
Đáp án : D Phương pháp giải :
- Giải phương trình lượng giác cơ bản: \(\cot x = \cot \alpha \Leftrightarrow x = \alpha + k\pi \,\,\left( {k \in \mathbb{Z}} \right)\). - Cho nghiệm tìm được thuộc \(\left[ { - 50\pi ;0} \right]\), tìm số các giá trị nguyên $k$ thỏa mãn. - Số các số nguyên từ $a$ đến $b$ là $b-a+1$ số ($a$ và $b$ cũng là các số nguyên). Lời giải chi tiết :
Ta có: \(\cot 20x = 1 \Leftrightarrow 20x = \dfrac{\pi }{4} + k\pi \) \( \Leftrightarrow x = \dfrac{\pi }{{80}} + \dfrac{{k\pi }}{{20}}\,\,\left( {k \in \mathbb{Z}} \right)\). Theo bài ra ta có: \(\begin{array}{l}x \in \left[ { - 50\pi ;0} \right]\\ \Leftrightarrow - 50\pi \le \dfrac{\pi }{{80}} + \dfrac{{k\pi }}{{20}} \le 0\\ \Leftrightarrow - 50 \le \dfrac{1}{{80}} + \dfrac{k}{{20}} \le 0\\ \Leftrightarrow - \dfrac{{4001}}{4} \le k \le - \dfrac{1}{4}\\ \Leftrightarrow -1000,25 \le k \le - 0,25\end{array}\) Mà \(k \in \mathbb{Z}\)\( \Rightarrow -1000 \le k \le -1\) \( \Rightarrow k \in \left\{ { - 1000; - 999;....; - 2; - 1} \right\}\) Tập trên có $-1-(-1000)+1=1000$ phần tử suy ra có $1000$ giá trị nguyên của $k$ thỏa mãn. Vậy phương trình đã cho có $1000$ nghiệm thỏa mãn yêu cầu bài toán.
Câu 24 :
Giải phương trình \(\cos 3x\tan 5x = \sin 7x\).
Đáp án : B Phương pháp giải :
- Tìm ĐKXĐ. - Sử dụng công thức \(\tan 5x = \dfrac{{\sin 5x}}{{\cos 5x}}\). - Sử dụng công thức biến đổi tích thành tổng: \(\sin a\cos b = \dfrac{1}{2}\left[ {sin\left( {a + b} \right) + sin\left( {a - b} \right)} \right]\). - Giải phương trình lượng giác cơ bản: \(\sin x = \sin \alpha \Leftrightarrow \left[ \begin{array}{l}x = \alpha + k2\pi \\x = \pi - \alpha + k2\pi \end{array} \right.\,\,\left( {k \in \mathbb{Z}} \right)\). Lời giải chi tiết :
ĐKXĐ: \(\cos 5x \ne 0 \Leftrightarrow 5x \ne \dfrac{\pi }{2} + m\pi \Leftrightarrow x \ne \dfrac{\pi }{{10}} + \dfrac{{m\pi }}{5}\,\,\left( {m \in \mathbb{Z}} \right)\). \(\begin{array}{l}\,\,\,\,\,\,\cos 3x\tan 5x = \sin 7x\\ \Leftrightarrow \cos 3x\sin 5x = \sin 7x\cos 5x\\ \Leftrightarrow \dfrac{1}{2}\left( {\sin 8x + \sin 2x} \right) = \dfrac{1}{2}\left( {\sin 12x + \sin 2x} \right)\\ \Leftrightarrow \sin 8x + \sin 2x = \sin 12x + \sin 2x\\ \Leftrightarrow \sin 12x = \sin 8x\\ \Leftrightarrow \left[ \begin{array}{l}12x = 8x + k2\pi \\12x = \pi - 8x + k2\pi \end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l}x = \dfrac{{k\pi }}{2}\\x = \dfrac{\pi }{{20}} + \dfrac{{k\pi }}{{10}}\end{array} \right.\,\,\left( {k \in \mathbb{Z}} \right)\end{array}\) Đối chiếu điều kiện ta có: \(\begin{array}{l}\,\,\,\,\,\,\dfrac{{k\pi }}{2} \ne \dfrac{\pi }{{10}} + \dfrac{{m\pi }}{5}\,\,\left( {k,\,\,m \in \mathbb{Z}} \right)\\ \Leftrightarrow 5k \ne 1 + 2m\\ \Leftrightarrow k \ne \dfrac{{1 + 2m}}{5}\end{array}\) Do \(k \in \mathbb{Z}\) nên: \(k = \dfrac{{1 + 2m}}{5} \Leftrightarrow \dfrac{{1 + 2m}}{5}\) là số nguyên. Mà \(1 + 2m\) luôn lẻ nên \(\dfrac{{1 + 2m}}{5}\) không chia hết cho 2 với mọi \(m\). Do đó, nếu \(k \ne \dfrac{{1 + 2m}}{5}\) thì \(k\) phải là số nguyên chẵn. \( \Rightarrow k\) chẵn, đặt \(k = 2n\), khi đó ta có \(x = \dfrac{{2n\pi }}{2} = n\pi \) \(\left( {n \in \mathbb{Z}} \right)\). \(\begin{array}{l}\,\,\,\,\,\,\dfrac{\pi }{{20}} + \dfrac{{k\pi }}{{10}} \ne \dfrac{\pi }{{10}} + \dfrac{{m\pi }}{5}\,\,\left( {k,\,\,m \in \mathbb{Z}} \right)\\ \Leftrightarrow 1 + 2k \ne 2 + 4m\end{array}\) Vì \(1 + 2k\) lẻ, \(2 + 4m\) chẵn nên \(1 + 2k \ne 2 + 4m\) luôn đúng với mọi \(k,\,\,m \in \mathbb{Z}\). Vậy nghiệm của phương trình đã cho là: \(x = n\pi ;\,\,x = \dfrac{\pi }{{20}} + \dfrac{{k\pi }}{{10}}\,\,\left( {k,\,\,n \in \mathbb{Z}} \right)\).
Câu 25 :
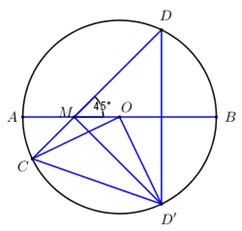
Cho đường tròn \(\left( {O;R} \right)\) đường kính \(AB\). Điểm \(M\) nằm trên \(AB\). Qua \(AB\) kẻ dây \(CD\) tạo với \(AB\) một góc \({45^0}\). Gọi \(D'\) là điểm đối xứng của \(D\) qua \(AB\). Tính \(M{C^2} + MD{'^2}\) theo \(R\)?
Đáp án : A Phương pháp giải :
Áp dụng định lí Pytago và các tính chất của đường trung trực. Lời giải chi tiết :
\(D' = \) Đ\(_{AB}\left( D \right) \Rightarrow AB\) là trung trực của \(DD' \Rightarrow MD = MD'\) và \(\angle DMB = \angle D'MB = {45^0}\). \( \Rightarrow \angle DMD' = {90^0} \Rightarrow \Delta MDD'\) vuông cân tại \(M\). \( \Rightarrow \angle MDD' = {45^0}\). Mà \(\angle MDD' = \dfrac{1}{2}\angle COD'\) (góc nội tiếp và góc ở tâm cùng chắn cung \(CD'\)) \( \Rightarrow \angle COD' = {90^0} \Rightarrow \Delta OCD'\) vuông cân tại \(O\). Do $O\in AB$ là trung trực của \(DD'\Rightarrow OD=OD'=R\Rightarrow D'\in \left( O;R \right)\). Áp dụng định lí Pytago trong tam giác vuông \(OCD'\) ta có : \(CD{{'}^{2}}=O{{C}^{2}}+OD{{'}^{2}}={{R}^{2}}+{{R}^{2}}=2{{R}^{2}}\). Ta có \(\angle DMD' = {90^0}\) (cmt) \( \Rightarrow \angle CMD' = {90^0} \Rightarrow \Delta CMD'\) vuông tại \(M\). Áp dụng định lí Pytago trong tam giác vuông \(CMD'\) ta có : \(M{C^2} + MD{'^2} = CD{'^2} = 2{R^2}\). |














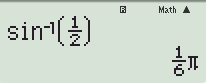





Danh sách bình luận