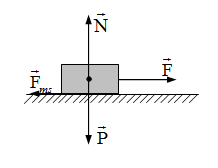
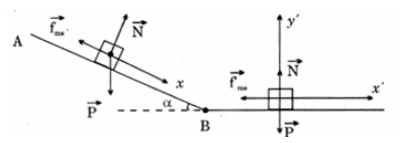
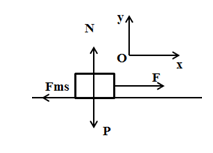
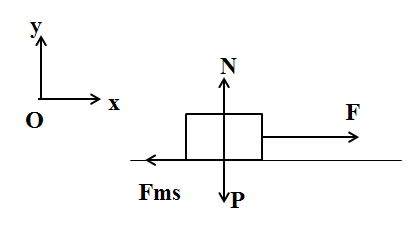
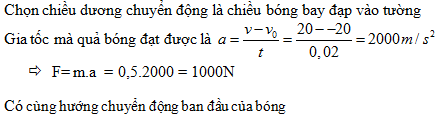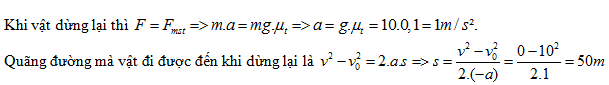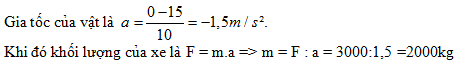50 bài tập Ôn tập chương 1, chương 2 (Phần 1)Làm bàiQuảng cáo
Câu hỏi 1 : Ôtô chuyển động thẳng đều mặc dù có lực kéo vì:
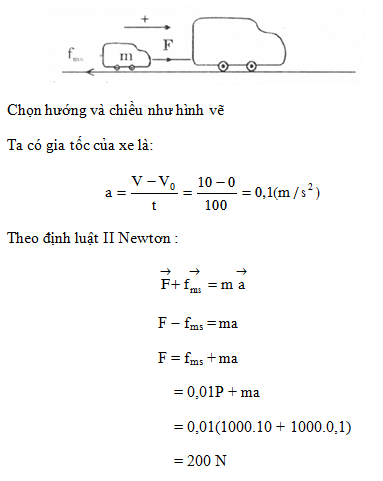
Đáp án: C Lời giải chi tiết: Oto chuyển động thẳng đều mặc dù có lực kéo vì các lực tác dụng vào oto đều bằng nhau Câu hỏi 2 : Một xe tải kéo một ô tô bằng dây cáp. Từ trạng thái đứng yên sau 100s ô tô đạt vận tốc V = 36km/h. Khối lượng ô tô là m = 1000 kg. Lực ma sát bằng 0,01 trọng lực ô tô. Tính lực kéo của xe tải trong thời gian trên. Phương pháp giải: Lời giải chi tiết: Câu hỏi 3 : Xe ô tô khối lượng 1tấn bắt đầu chuyển động trên đường nằm ngang AB không vận tốc đầu từ A, với gia tốc 1m/s2. Tới B xe đạt vận tốc 10m/s, biết hệ số ma sát trượt giữa xe và đường là 0,1. Cho g = 10m/s2 Tìm quãng đường AB và thời gian chuyển động của xe từ A đến B? Tính độ lớn lực kéo của đầu của động cơ khi đó (coi lực kéo của động cơ có phương nằm ngang)? 3. Tới B xe tắt máy lên dốc nghiêng BC với góc nghiêng của dốc so với mặt phẳng ngang là 300. Tìm gia tốc của xe khi lên dốc, quãng đường lớn nhất mà xe lên được trên dốc. Biết hệ số ma sát trên mặt phẳng nghiêng vẫn bằng 0,1. Phương pháp giải: Lời giải chi tiết: c. PTĐL II Niu – tơn: \(\overrightarrow P + \overrightarrow {{F_{ms}}} + \overrightarrow N = m\overrightarrow {{a_2}} \) Chiếu lên hai trục toạ độ, kết hợp lại ta được: a2 = - g(sinα + µ.cosα) Thay số ta được: a2 = -10(sin30 + 0,1.cos30) = -5,866 m/s2 (với chiều dương là chiều chuyển động) Quãng đường lớn nhất vật lên được mặt phẳng nghiêng: \({S_{m{\rm{ax}}}} = {{{v^2} - v_B^2} \over {2{a_2}}} = {{ - {{10}^2}} \over {2.( - 5,866)}} = 8,52m\) Câu hỏi 4 : Quả bóng khối lượng 500g bay với vận tốc 72km/h đến đập vuông góc vào một bức tường rồi bật trở ra theo phương cũ với vận tốc 54km/h. Thời gian va chạm là 0,05s. Tính lực của bóng tác dụng lên tường
Đáp án: D Lời giải chi tiết: Câu hỏi 5 : Một quả bóng , khối lượng 500g bay với tốc độ 20 m/s đập vuông góc vào bức tường và bay ngược lại với tốc độ 20m/s.Thời gian va đập là 0,02 s. Lực do bóng tác dụng vào tường có độ lớn và hướng:
Đáp án: A Lời giải chi tiết: Câu hỏi 6 : Một hợp lực 2N tác dụng vào 1 vật có khối lượng 2kg lúc đầu đứng yên, trong khoảng thời gian 2s. Đoạn đường mà vật đó đi được trong khoảng thời gian đó là :
Đáp án: B Lời giải chi tiết: Câu hỏi 7 : Một quả bóng có khối lượng 500g đang nằm trên mặt đất thì bị đá bằng một lực 200N. Nếu thời gian quả bóng tiếp xúc với bàn chân là 0,02s thì bóng sẽ bay đi với tốc độ bằng :
Đáp án: C Lời giải chi tiết: Gia tốc mà lực gây ra cho quả bóng là a = F:m = 200 : 0,5 = 400 m/s2 Khi đó vận tốc mà vạt đạt được là : v = a.t = 400.0,02 = 8 m/s Câu hỏi 8 : Một lực không đổi tác dụng vào một vật có khối lượng 5kg làm vận tốc của nó tăng dần từ 2m/s đến 8m/s trong 3s. Độ lớn của lực tác dụng vào vật là :
Đáp án: C Lời giải chi tiết: Câu hỏi 9 : Một hợp lực 1 N tác dụng vào một vật có khối lượng 2kg lúc đầu đứng yên, trong khoảng thời gian 2s. Quãng đường mà vật đi được trong khoảng thời gian đó là:
Đáp án: B Lời giải chi tiết: Câu hỏi 10 : Một ô tô khối lượng 1 tấn đang chuyển động với tốc độ 72km/h thì hãm phanh, đi thêm được 500m rồi dừng lại. Chọn chiều dương là chiều chuyển động. Lực hãm tác dụng lên xe là:
Đáp án: D Lời giải chi tiết: Câu hỏi 11 : Một vật có khối lượng 50kg chuyển động nhanh dần đều với vận tốc ban đầu 0,2m/s và khi đi được quãng đường 50cm vận tốc đạt được 0,9m/s thì lực tác dụng .
Đáp án: A Lời giải chi tiết: Câu hỏi 12 : Một vật có vận tốc đầu có độ lớn là 10m/s trượt trên mặt phẳng ngang . Hệ số ma sát trượt giữa vật và mặt phẳng là 0,10. Hỏi vật đi được 1 quãng đường bao nhiêu thì dừng lại ? Lấy g = 10m/s2.
Đáp án: B Lời giải chi tiết: Câu hỏi 13 : Một xe hơi chạy trên đường cao tốc với vận tốc có độ lớn là 15m/s. Lực hãm có độ lớn 3000N làm xe dừng trong 10s. Khối lượng của xe là
Đáp án: B Lời giải chi tiết: Câu hỏi 14 : Một xe ôtô có khối lượng 2 tấn. Bắt đầu khởi hành, sau khi đi được thời gian 20 giây ô tô đạt tốc độ 72km/h. Biết hệ số ma sát giữa xe và mặt đường là 0,2, lấy g=10m/s. a. Tính gia tốc của ô tô và quãng đường xe đi được trong thời gian trên. b. Muốn xe dừng lại, tài xế tắt máy và hãm phanh với lực hãm 2000N. Tính thời gian từ lúc phanh cho đến lúc xe dừng hẳn. Lời giải chi tiết: Câu hỏi 15 : Một vật trượt không vận tốc đầu từ đỉnh một khối nêm hình tam giác vuông dài l = 20m, nghiêng 300 so với mặt phẳng nằm ngang. Nêm có thể trượt không ma sát trên mặt phẳng ngang. Hệ số ma sát giữa vật và nêm là 0,2. Lấy g = 10m/s2. a. Giữ nêm đứng yên. Tính vận tốc của vật tại chân nêm và thời gian vật trượt trên nêm . b. Cho nêm chuyển động về phía ngược chiều chuyển động của vật với gia tốc a0 theo phương ngang. Thời gian vật trượt từ đỉnh đến chân nêm là 3,15s. Tính gia tốc a0 của nêm. Lời giải chi tiết: Câu hỏi 16 : Một vật có khối lượng m = 2kg, đang nằm yên thì được kéo bởi lực F = 5N có phương ngang, làm vật dịch chuyển trên mặt sàn. Trong suốt quá trình chuyển động, vật chịu tác dụng của lực cản Fc có độ lớn không đổi 2 N. Tìm gia tốc của xe. Sau khi vật chuyển động 2 s thì lực kéo F ngừng tác dụng lên vật. Tìm quãng đường vật đi thêm được từ khi lực F ngừng tác dụng đến khi vật dừng lại.Lời giải chi tiết: Câu hỏi 17 : Một lực có độ lớn 10 N tác dụng vào một vật có khối lượng2 kglúc đầu đứng yên, làm cho vật chuyển động thẳng nhanh dần đều. a) Tính gia tốc của vật. b) Tính quãng đường mà vật đi được trong 20 giây. Lời giải chi tiết: Câu hỏi 18 : Môṭ vâṭ có khối lươṇg m đươc̣ ném lên doc̣ theo măṭ môṭ phẳng nghiêng góc a so với măṭ phẳng ngang với tốc độ ban đầu v0 .Tìm độ cao h mà vật lên được , biết hê ̣số ma sát giữa vật và mặt phẳng nghiêng là k.
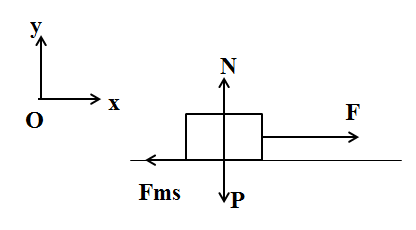
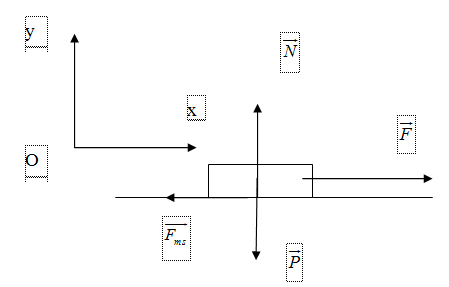
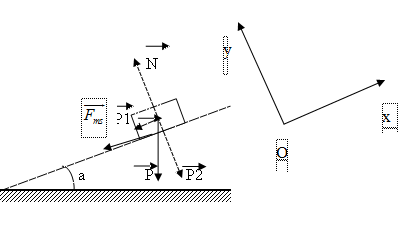
Đáp án: A Phương pháp giải: động học và động lực học chất điểm Lời giải chi tiết: Chọn hệ quy chiếu gắn với mặt đất, trục Ox dọc theo mặt phẳng nghiêng, chiều hướng lên. Oy vuông góc với Ox, chiều hướng lên. Các lực tác dụng lên vật gồm trọng lực P, phản lực N, lực ma sát. \(\begin{array}{l} Câu hỏi 19 : Một vật có khối lượng m = 8kg nằm yên trên mặt bàn nằm ngang. Người ta tác dụng lên vật một lực \(\vec F\) có phương ngang để kéo vật chuyển động. Biết hệ số ma sát trượt giữa vật với mặt bàn là μ = 0,1, lực \(\vec F\) có độ lớn là 20N, lấy g = 10m/s2. a. Vẽ các lực tác dụng lên vật. b. Xác định độ lớn gia tốc chuyển động của vật. c.Xác định vận tốc của vật sau 8s, kể từ lúc tác dụng lực \(\vec F\) . d/.Sau thời gian 8s trên thì ngưng tác dụng lực \(\vec F\) , xác định thời gian vật chuyển động từ lúc ngưng tác dụng lực \(\vec F\) đến khi vật dừng lại. Phương pháp giải: Lời giải chi tiết: a/.Vật chịu tác dụng của trọng lực \(\vec P\) , phản lực \(\vec N\), lực kéo \(\vec F\) và lực ma sát \({\vec F_{ms}}\) như hình vẽ. b/. Chọn hệ quy chiếu gắn với mặt đất Theo phương thẳng đứng: N = P =mg (1) Định luật II Newton theo phương ngang: \(a = \frac{{F - {F_{ms}}}}{m} = \frac{{F - \mu N}}{m}\) (2) Từ (1) và (2): \(a = \frac{{F - \mu mg}}{m}\) = 1,5 m/s2 c/. Vận tốc của vật sau 8 giây chuyển động: v = a.t = 8.1,5 = 12m/s d/.Sau khi ngừng tác dụng của lực F chỉ còn lực ma sát tác dụng lên vật. Gia tốc của vật sau khi ngưng tác dụng lực \(\vec F\) :\(a = - \mu g\)=-1m/s2. Thời gian kể từ khi ngưng tác dụng lực đến khi vật dừng lại là: t=-v0/a=12s
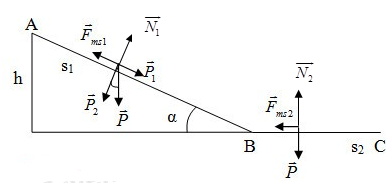
Câu hỏi 20 : Một vật có khối lượng 100 kg trượt không ma sát không vận tốc đầu từ đỉnh một mặt phẳng nghiêng cao 5 m, nghiêng góc \(\alpha \)= 300 so với phương ngang. Lấy g = 10 m/s2. 1. Tìm khoảng thời gian vật chuyển động trên mặt phẳng nghiêng và vận tốc vật ở chân mặt phẳng nghiêng 2. Khi vật trượt hết mặt phẳng nghiêng, vật tiếp tục trượt chậm dần đều trên mặt phẳng ngang. Biết hệ số ma sát giữa vật và mặt phẳng ngang là \(\mu = \) 0,4. Tính thời gian và quãng đường vật đi được trên mặt phẳng ngang. Phương pháp giải: AH=h=5(m) M=100kg α=300 vA=0 g=10(m/s2) tAB=? vB=? µBD=0,4tBD=? SBD=? Lời giải chi tiết: Phương trình động lực học: \(\vec N + \vec P = m\vec a\) Chiếu phương trình véc tơ lên trục oy vuông góc với mặt phẳng nghiêng, chiều hướng lên trên ta được: \( - mg.cos{30^0} + N = 0 = > Q = N = mg.cos30\) Chiếu phương trình véc tơ lên trục ox song song với mặt phẳng nghiêng ta được \(P.sin30{\rm{ }} = {\rm{ }}ma = > a = g.sin30 = 10.\frac{1}{2} = 5m/{s^2}\) Áp dụng công thức \(v_B^2 - v_A^2 = 2a{S_{AB}}\) Vì :
Ta có vì \({v_A} = 0\) nên ta có : \({v_B} = \sqrt {2a{S_{AB}}} = \sqrt {2.5.10} = 10m/s\) Thời gian vật chuyển động trên mặt phẳng nghiêng AB \({v_B} = {v_0} + at = > {t_{AB}} = \frac{{{v_B} - {v_A}}}{a} = \frac{{10 - 0}}{5} = 2\left( s \right)\) 2. Vẽ hình trên phương ngang, phân tích lực tác dụng vào vật Khi vật trượt trên mặt phẳng ngang có ma sát thì ta có phương trình ĐLH của vật là: \({\vec F_{ms}} + \vec N + \vec P = m\vec a\) Chiếu phương trình véc tơ lên trục oy vuông góc với mặt phẳng ngang BD và vuông góc với BD ta được \( - P{\rm{ }} + {\rm{ }}N{\rm{ }} = {\rm{ }}0 = > P = N\) Chiếu phương trình véc tơ lên trục 0X song song với mặt phẳng ngang BD ta được: \( - {F_{ms}} = {\rm{ }}ma = > a = - \frac{{{F_{ms}}}}{m} = - \frac{{\mu mg}}{m} = - \mu g = > a = - 0,4.10 = - 4(m/{s^2})\) Quãng đường vật đi được trên mặt phẳng ngang ADCT: \(v_C^2 - v_B^2 = 2a{S_{BC}}\) \( = > {S_{BC}} = \frac{{ - v_B^2}}{{2a}} = \frac{{ - {{10}^2}}}{{2.\left( { - 4} \right)}} = 12,5\left( m \right)\) Thời gian vật đi được trên mặt phẳng ngang : \({t_{BC}} = \frac{{{v_C} - {v_B}}}{a} = \frac{{0 - 10}}{{ - 4}} = 2,5\left( s \right)\) Câu hỏi 21 : Một ôtô có khối lượng 1 tấn đang chuyển động với vận tốc 18km/h thì tăng tốc chuyển động thẳng nhanh dần đều sau khi đi được quãng đường 50m thì đạt vận tốc 54km/h. Biết hệ số ma sát giữa xe và mặt đường là 0,02. Lấy g = 10m/s2. a. Tìm lực kéo động cơ xe? b. Sau đó tài xế tắt máy, xe chuyển động thẳng chậm dần đều. Biết rằng lực ma sát giữa xe và mặt đường không đổi. Tìm thời gian từ lúc tắt máy đến khi xe dừng lại hẳn? Phương pháp giải: Áp dụng định luật 2 Niu tơn và các lực cho chuyển động Lời giải chi tiết: Ta có m = 1000kg, v0 = 18km/h = 5m/s, s = 50m, v = 54km/h = 15m/s. a) Gia tốc chuyển động của xe: a = (v2 – v02)/2S = 2,2m/s2 Áp dụng định luật 2 Niu tơn ta được: F – Fms = ma F - µmg = ma F = 2400N b) Gia tốc khi tắt máy: a’ = - Fms/m = - 0,2m/s2 Thời gian từ khi tắt máy đến khi dừng hẳn: 0 = 15 – 0,2t Vậy t = 30s Câu hỏi 22 : Một vật có khối lượng 10kg đang đặt trên mặt sàn nằm ngang được kéo bằng một sợi dây với lực có độ lớn 30N và có phương song song với sàn. Cho hệ số ma sát giữa vật và sàn là 0,25. Lấy g = 10m/s2. a) Vẽ hình. Tính độ lớn gia tốc của vật? b) Khi tốc độ của vật đạt 5m/s thì dây kéo bị đứt. Tính quãng đường đi được tất cả của vật trên sàn?
Đáp án: D Phương pháp giải: - Áp dụng định luật II Niu tơn - Trọng lực P = mg - Lực ma sát Fms = µN - Công thức liên hệ v2 – v02 = 2aS Lời giải chi tiết: a) Áp dụng định luật II Niu tơn ta có: \(\overrightarrow{P}+\overrightarrow{N}+\overrightarrow{F}+\overrightarrow{{{F}_{ms}}}=m\overrightarrow{a}\) Chiếu lên Oy ta được N = P = mg Chiếu lên Ox ta được F – Fms = ma --> F - µN = ma --> 30 – 0,25.10.10 = 10.a --> a = 0,5m/s2 b) Khi vật đạt tốc độ 5m/s thì nó đã đi được quãng đường : 52 = 2.0,5.S1 --> S1 = 25m Dây bị đứt nên không còn lực kéo F tác dụng Vậy –Fms = ma’ --> a’ = - 0,25m/s2 Khi đó nó đi thêm được quãng đường nữa thì dừng lại là: 02 – 52 = 2.(-0,25).S2 --> S2 = 50m Vậy tổng quãng đường vật đi được là S = S1 + S2 = 75m
Câu hỏi 23 : Một ôtô có khối lượng 1,5 tấn chuyển động trên mặt đường nằm ngang cóhệ số ma sát µ = 0,2. Sau khi khởi hành được 10 giây, ôtô đạt vận tốc 72km/h. Lấy g = 10m/s2. a) Tìm gia tốc và lực phát động của ôtô. b) Sau khi khởi hành bao lâu vật đi được quãng đường bằng quãng đường vật đi được trong giây thứ 10.
Đáp án: C Phương pháp giải: - Áp dụng định luật 2 Niu tơn - Công thức gia tốc a = (v-v0)/t - Công thức tính quãng đường s = vot + 0,5at2 Lời giải chi tiết: M = 1,5.103kg, v0 = 0, v = 72km/h = 20m/s, t = 10s a) Gia tốc của xe: a = (v – v0)/t = 2m/s2 Lực phát động: F – Fms = ma -> F = Fms + ma = µmg + ma = 6000N b) Quãng đường đi được sau 10s : S10 = 0,5.a.102 = 100m Quãng đường đi được sau 9s: S9 = 0,5.a.92 = 81m Quãng đường đi được trong giây thứ 10: S’= S10 – S9 = 9m Thời gian từ lúc khởi hành để xe đi được 9m: 9 = 0,5.a.t2 -> t = 3s Câu hỏi 24 : Một xe có khối lượng 1 tấn đang đi với vận tốc 18 km/h thì tăng tốc, sau 10 s thì đạt vận tốc 72 km/h.
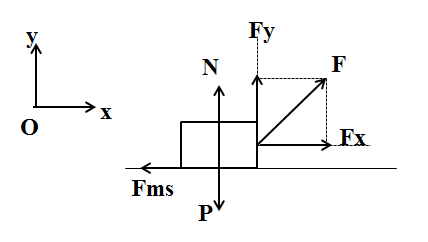
Đáp án: D Phương pháp giải: a) Áp dụng công thức gia tốc \(a = \frac{{{v_2} - {v_1}}}{{\Delta t}}\) b) Vẽ hình biểu diễn các lực tác dụng lên xe trên hệ trục tọa độ Oxy: lực của động cơ, lực ma sát, trọng lực, phản lực N. Dùng định luật II Niu – Tơn: \(\sum {\overrightarrow F } = m.\overrightarrow a \) . Sau đó chiếu phương trình định luật II lên các trục tọa độ. Và tìm F. c) DÙng phương trình độc lập với thời gian : \({v^2} - v_0^2 = 2as\) Lời giải chi tiết: Đổi 18km/h = 5 m/s; 72 km/s = 20m/s. a. Gia tốc của xe là : \(a = \frac{{{v_2} - {v_1}}}{{\Delta t}} = \frac{{20 - 5}}{{10}} = 1,5m/{s^2}\) b. Ta có hình vẽ: Chọn hệ quy chiếu gắn với mặt đất, các lực tác dụng lên vật như trên hình vẽ Vật chuyển động thẳng với gia tốc = 1,5 m/s2, theo định luật I và II Niu – tơn ta có \(\overrightarrow F + \overrightarrow P + \overrightarrow N + \overrightarrow {{F_{ms}}} = m.\overrightarrow a \) Chiếu lên hai trục Ox, Oy ta được \(\left\{ \begin{array}{l} Vậy lực của động cơ là 2500N c) Khi dừng nhấn ga, không còn lực của động cơ tác dụng nữa nên \(\overrightarrow P + \overrightarrow N + \overrightarrow {{F_{ms}}} = m.\overrightarrow {a'} \) Chiếu lên hai trục Ox, Oy ta được \(\left\{ \begin{array}{l} Vậy xe chuyển động chậm dần đều với gia tốc a = -2 m/s2. Quãng đường xe đi được đến khi dừng lại là s, được xác định bởi
Vậy vật đi được 100m trước khi dừng hẳn Câu hỏi 25 : Một vật chuyển động thẳng biến đổi đều trên mặt phẳng ngang từ trạng thái đứng yên. Sau 2s kể từ lúc bắt đầu chuyển động, vật đạt tốc độ 3m/s. Cho g = 10 m/s2. a. Tính độ lớn gia tốc của chuyển động ? b. Biết vật có khối lượng 2kg được kéo bằng lực \(\overrightarrow{F}\) nằm ngang, có độ lớn F = 7 N. Biết chuyển động của vật trượt trên mặt phẳng ngang có ma sát trượt. Vẽ hình biểu diễn các lực tác dụng lên vật và tính hệ số ma sát trượt giữa vật và sàn ? c. Để vật chuyển động thẳng đều người ta kéo vật bằng lực \({{\overrightarrow{F}}_{1}}\) nghiêng chếch lên trên và hợp với mặt phẳng ngang góc α (với sinα = 0,6). Tìm độ lớn của lực F1?
Đáp án: D Phương pháp giải: - Vận tốc tức thời : v = v0 + at - Định luật 2 Niu tơn: \(\overrightarrow{F}=m\overrightarrow{a}\) - Lực ma sát giữa vật và sàn: Fms = µN - Vật chuyển động thẳng đều thì hợp lực tác dụng bằng 0 Lời giải chi tiết: a) Ta có: v0 = 0; t = 2s; v = 3m/s Gia tốc của vật: \(\;v = {v_0} + at \Rightarrow 3 = 2a \Rightarrow a = 1,5m/{s^2}\) b) Áp dụng định luật 2 Niu tơn: \(\vec P + \vec N + \vec F + \overrightarrow {{F_{ms}}} = m\vec a\) Chiếu biểu thức trên lên trục Oy ta được: \( - P + N = 0 \Rightarrow N = P = mg\) Chiếu biểu thức trên lên trục Ox ta được: \(F - {F_{ms}} = ma \Leftrightarrow F - \mu N = ma \Rightarrow F - \mu mg = ma \Rightarrow 7 - \mu .2.10 = 2.1,5 \Rightarrow \mu = 0,2\) c) Áp dụng định luật 2 Niu tơn: \(\vec P + \vec N + {\vec F_1} + \overrightarrow {{F_{ms}}} = m\vec a\) Chiếu biểu thức trên lên trục Oy ta được: \(N-P + Fsin\alpha = 0 \Rightarrow N = mg - Fsin\alpha \) Chiếu biểu thức trên lên trục Ox ta được: \({F_1}cos\alpha --{F_{ms}} = ma \Rightarrow {F_1}.cos\alpha - \mu N = ma \Rightarrow {F_1}.cos\alpha --0,2.(2.10 - 7.sin\alpha ) = 2.1,5\) Với sinα = 0,6 thì cosα = 0,8 Thay vào ta được F1 = 7,7N
Câu hỏi 26 : Một vật khối lượng 4kg được kéo bởi một lực hướng lên hợp với phương ngang một góc α= 300. Lực F có độ lớn 16N. Biết sau khi bắt đầu chuyển động 2s từ trạng thái đứng yên vật đi được quãng đường 4m. Lấy g = 10m/s2. Tính hệ số ma sát giữa vật và mặt ngang.
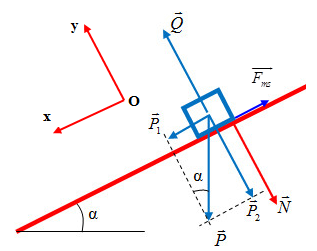
Đáp án: B Phương pháp giải: - Quãng đường đi được: S = v0t + 0,5at2 - Lực ma sát: Fms = µN - Trọng lực P = mg - ÁP dụng định luật 2 Niu tơn: \(\overrightarrow{F}=m\overrightarrow{a}\) và tiến hành chiếu biểu thức lên trục tọa độ thích hợp Lời giải chi tiết: Quãng đường vật đi được: \(S = {v_0}t + \frac{1}{2}a{t^2} \Rightarrow 4 = 0 + \frac{1}{2}a{.2^2} \Rightarrow a = \sqrt 2 m/{s^2}\) Các lực tác dụng lên vật được biểu diễn như hình vẽ. Áp dụng định luật 2 Niu tơn: \(\overrightarrow P + \overrightarrow N + \overrightarrow F + \overrightarrow {{F_{ms}}} = m\overrightarrow a \) Chiếu biểu thức lên trục Oy ta được: N – P = 0 => N = P = mg Chiếu biểu thức lên trục Ox ta được: \(F - {F_{ms}} = ma \Leftrightarrow F - \mu N = ma \Leftrightarrow 16 - \mu .4.10 = 4\sqrt 2 \Rightarrow \mu = 0,258\) Câu hỏi 27 : Một vật trượt không vận tốc đầu từ đỉnh mặt phẳng nghiêng dài 10m nghiêng 300 so với phương ngang. Hệ số ma sát trượt giữa vật và mặt phẳng nghiêng là 0,2. Cho g = 10m/s2 a) Vẽ các lực tác dụng lên vật khi trượt, tính gia tốc của vật? b) Tìm vận tốc khi vật đến chân mặt phẳng nghiêng? c) Tính thời gian vật đi hết quãng đường 2m cuối trước khi đến chân mặt phẳng nghiêng? Phương pháp giải: a) Các lực tác dụng lên vật: Trọng lực, phản lực, lực ma sát. b) Áp dụng công thức độc lập với thời gian : \({v^2}--{v_0}^2 = 2as\) c) Áp dụng công thức tính quãng đường : \(S = {v_0}.t + \frac{1}{2}a.{t^2}\) Tìm thời gian đi hết 8m và đi hết 10m, sau đó lấy t10 – t8 Lời giải chi tiết: Tóm tắt: l = 10m ; α = 300; μ = 0,2 ; g = 10m/s2 a) Vẽ các lực tác dụng lên vật khi trượt, tính gia tốc của vật? b) Tìm vận tốc khi vật đến chân mặt phẳng nghiêng? c) Tính thời gian vật đi hết quãng đường 2m cuối trước khi đến chân mặt phẳng nghiêng? Giải :
- Áp dụng định luật 2 Niuton: \(\overrightarrow N + \overrightarrow P + \overrightarrow {{F_{ms}}} = m.\overrightarrow a \)
Chiếu lên hai trục Ox và Oy ta được: \(\left\{ \begin{array}{l} Mà \({F_{ms}} = \mu .N \Rightarrow a = \frac{{g.m.\sin \alpha - \mu .m.g.cos\alpha }}{m} = g.(sin\alpha - \mu .cos\alpha )\) Vậy:\(a = g.\left( {sin{{30}^0} - \mu .cos{{30}^0}} \right) = 3,27\left( {m/{s^2}} \right)\) b) Khi tới chân mặt phẳng nghiêng vật đi được quãng đường S = 10m. Áp dụng công thức: \({v^2} - {0^2} = 2as\; \Rightarrow v = 8,09m/s\) (do v0 = 0) c) Thời gian vật đi hết S1 = 8m đầu tiên trên mặt nghiêng là t1, Ta có: \({S_1} = \frac{1}{2}.a.t_1^2 \Rightarrow {t_1} = \sqrt {\frac{{2.{S_1}}}{a}} = \sqrt {\frac{{2.8}}{{3,27}}} = 2,21s\) Thời gian vật đi hết S = 10m trên mặt nghiêng là t, tính được t: Áp dụng công thức \(S = \frac{1}{2}.a.{t^2} \Rightarrow t = \sqrt {\frac{{2.S}}{a}} = \sqrt {\frac{{2.10}}{{3,27}}} = 2,47s\) Thời gian vật đi hết 2m cuối trên mặt nghiêng là: \(\Delta t{\rm{ }} = t--{t_1} = 2,47 - 2,21 = 0,26\left( s \right)\)
Câu hỏi 28 : Một vật trượt không vận tốc đầu từ đỉnh của một mặt phẳng nghiêng dài L = 10m, góc nghiêng \(\alpha ={{30}^{0}}\). Lấy g = 10m/s2, hệ số ma sát giữa vật và mặt phẳng nghiêng là 0,2. Tính gia tốc và vận tốc của vật tại chân mặt phẳng nghiêng.
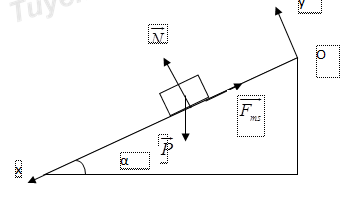
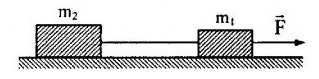
Đáp án: B Phương pháp giải: Phương pháp động lực học: Bước 1: Chọn vật (hệ vật) khảo sát. Bước 2: Chọn hệ quy chiếu (Cụ thể hoá bằng hệ trục toạ độ vuông góc; Trục toạ độ Ox luôn trùng với phương chiều chuyển động; Trục toạ độ Oy vuông góc với phương chuyển động) Bước 3: Xác định các lực và biểu diễn các lực tác dụng lên vật trên hình vẽ. Bước 4: Viết phương trình hợp lực tác dụng lên vật theo định luật II Niu Tơn. \(\overrightarrow{{{F}_{hl}}}=\overrightarrow{{{F}_{1}}}+\overrightarrow{{{F}_{2}}}+...+\overrightarrow{{{F}_{n}}}=m.\overrightarrow{a}\) (*) (Tổng tất cả các lực tác dụng lên vật) Bước 5: Chiếu phương trình lực (*) lên các trục toạ độ Ox, Oy: Ox: F1x + F2x + … + Fnx = ma (1) Oy: F1y + F2y + … + Fny = 0 (2) Giải phương trình (1) và (2) ta thu được đại lượng cần tìm Lời giải chi tiết: Vật chịu tác dụng của 3 lực trên mặt phẳng nghiêng: + Trọng lực \(\overrightarrow{P}\) + Phản lực \(\overrightarrow{Q}\) + Lực ma sát: \(\overrightarrow{{{F}_{ms}}}\) Biểu diễn các lực tác dụng vào vật và chọn hệ trục toạ độ như hình vẽ: Ta có: \(\left\{ \begin{array}{l} Từ hình vẽ ta có: \(\left\{ \begin{array}{l} Áp dụng định luật II Niuton ta có : \(\overrightarrow{{{F}_{ms}}}+\overrightarrow{Q}+\overrightarrow{{{P}_{1}}}+\overrightarrow{{{P}_{2}}}=m.\overrightarrow{a}\,\,\,\left( * \right)\) Chiếu (*) lên Ox, Oy ta được : \(\begin{array}{l} Thay số ta được : \(a=10.\left( \sin 30-0,2.\cos 30 \right)=3,27m/{{s}^{2}}\) Ta có : \(v_{B}^{2}-v_{A}^{2}=2a.AB\Rightarrow {{v}_{B}}=\sqrt{v_{A}^{2}+2a.AB}=\sqrt{0+2.4,13.10}\approx 8,1m/s\) Chọn B. Câu hỏi 29 : Hai vật m1 = 5kg, m2 = 10kg được nối với nhau bằng một dây nhẹ, đặt trên mặt phẳng nằm ngang không ma sát. Tác dụng lực nằm ngang F = 18N lên vật m1. Vận tốc và quãng đường mỗi vật sau khi vật bắt đầu chuyển động 2s.
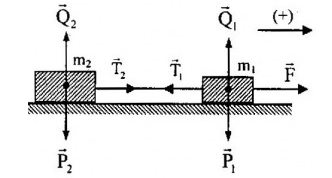
Đáp án: D Phương pháp giải: Chú ý: Nếu sợi dây không dãn thì các vật chuyển động cùng gia tốc và vận tốc và độ lớn lực căng dây là như nhau tại mọi điểm trên dây. Bước 1: Phân tích có nhưng lực nào tác dụng vào các vật (vẽ hình). Bước 2: Chọn hệ trục toạ độ cho các vật. Bước 3: Áp dụng định luật II Niuton cho từng vật. Bước 4: Chiếu biểu thức định luật II Niuton lên các trục toạ độ. Bước 5: Giải ra ẩn số của bài toán. Lời giải chi tiết:
Áp dụng định luật II Niuton cho từng vật ta có : \(\left\{ \begin{array}{l}\overrightarrow {{P_1}} + \overrightarrow {{Q_1}} + \overrightarrow F + \overrightarrow {{T_1}} = {m_1}\overrightarrow {{a_1}} \,\,\,\left( * \right)\\\mathop {{P_2}}\limits^ \to + \mathop {{Q_2}}\limits^ \to + \mathop {{T_2}}\limits^ \to + = {m_2}\mathop {{a_2}}\limits^ \to \,\,\,\left( {**} \right)\end{array} \right.\) Chiếu (*) và (**) lên phương ngang, theo chiều chuyển động của mỗi vật ta có: \(\left\{ \begin{array}{l}F - {T_1} = {m_1}{a_1}\\{T_2} = {m_2}{a_2}\end{array} \right.\) Do dây không dãn nên: \(\left\{ \begin{array}{l}{T_1} = {T_2} = T\\{a_1} = {a_2} = a\end{array} \right. \Rightarrow \left\{ \begin{array}{l}F - T = {m_1}a\\T = {m_2}a\end{array} \right. \Rightarrow F - {m_2}a = {m_1}a \Rightarrow a = \dfrac{F}{{{m_1} + {m_2}}}\) Thay số vào ta có: \(a = \dfrac{F}{{{m_1} + {m_2}}} = \dfrac{{18}}{{5 + 10}} = 1,2m/{s^2}\) Vận tốc của mỗi vật sau khi chuyển động được 2s là: \(v = {v_0} + at = 0 + 1,2.2 = 2,4m/s\) Quãng đường vật đi được sau khi chuyển động được 2s là: \(s = \dfrac{1}{2}a{t^2} = \dfrac{1}{2}.1,{2.2^2} = 2,4m\) Vậy sau 2s chuyển động vận tốc và quãng đường đi được của mỗi vật là: v = 2,4m/s và s = 2,4m Chọn D. Câu hỏi 30 : Một vật có khối lượng \(500g\) đang chuyển động thẳng đều với vận tốc \(18km/h\) thì chịu tác dụng của một lực \(\overrightarrow F \) có độ lớn \(2N\) ngược chiều chuyển động của vật. a) Tính độ lớn gia tốc của vật khi chịu tác dụng của lực \(\overrightarrow F \). b) Tính quãng đường và thời gian vật chuyển động từ khi chịu tác dụng của lực \(\overrightarrow F \) cho đến khi dừng lại. Phương pháp giải: a) Sử dụng biểu thức định luật II – Niuton: \(F = ma\) b) + Sử dụng hệ thức độc lập: \({v^2} - v_0^2 = 2as\) + Sử dụng biểu thức: \(a = \dfrac{{\Delta v}}{{\Delta t}}\) Lời giải chi tiết: a) Gia tốc của vật: \(a = \dfrac{{ - F}}{m} = \dfrac{{ - 2}}{{0,5}} = - 4m/{s^2}\) b) Vận tốc ban đầu của vật \({v_0} = 18km/h = 5m/s\) + Quãng đường vật đi được cho đến khi dừng lại: \(s = \dfrac{{{v^2} - v_0^2}}{{2a}} = \dfrac{{0 - {5^2}}}{{2.\left( { - 4} \right)}} = 3,125m\) + Thời gian vật chuyển động cho đến khi dừng lại: \(t = \dfrac{{\Delta v}}{a} = \dfrac{{v - {v_0}}}{a} = \dfrac{{0 - 5}}{{ - 4}} = 1,25s\) Câu hỏi 31 : Một vật có khối lượng m = 1500g được đặt trên một bàn dài nằm ngang. Biết hệ số ma sát giữa vật và mặt bàn là \(\mu = 0,2\). Lấy \(g = 10m/{s^2}\). Tác dụng lên vật một lực F = 4,5N song song với mặt bàn: a) Vẽ hình. Tính gia tốc của vật. (1,5đ) b) Vận tốc chuyển động của vật sau 2 giây kể từ khi tác dụng lực (0,5đ) Phương pháp giải: Bước 1: Chọn vật (hệ vật) khảo sát. Bước 2: Chọn hệ quy chiếu (Cụ thể hoá bằng hệ trục toạ độ vuông góc; Trục toạ độ Ox luôn trùng với phương chiều chuyển động; Trục toạ độ Oy vuông góc với phương chuyển động) Bước 3: Xác định các lực và biểu diễn các lực tác dụng lên vật trên hình vẽ. Bước 4: Viết phương trình hợp lực tác dụng lên vật theo định luật II Niu Tơn. \(\overrightarrow {{F_{hl}}} = \overrightarrow {{F_1}} + \overrightarrow {{F_2}} + ... + \overrightarrow {{F_n}} = m.\overrightarrow a \) (*) (Tổng tất cả các lực tác dụng lên vật) Bước 5: Chiếu phương trình lực (*) lên các trục toạ độ Ox, Oy: Ox: F1x + F2x + … + Fnx = ma (1) Oy: F1y + F2y + … + Fny = 0 (2) Giải phương trình (1) và (2) ta thu được đại lượng cần tìm b) Công thức tính vận tốc : \(v = {v_0} + at\) Lời giải chi tiết:
Ta có: \(\left\{ \begin{array}{l}{v_0} = 0\\m = 1500g = 1,5kg\\\mu = 0,2\\g = 10m/{s^2}\\F = 4,5N\end{array} \right.\) a) - Các lực tác dụng lên vật: Lực kéo \(\vec F\), lực ma sát \({\vec F_{ms}}\), trọng lực \(\vec P\), phản lực \(\vec N\) - Chọn hệ trục tọa độ: Ox nằm ngang, Oy thẳng đứng hướng lên trên. - Phương trình định luật II Niu-tơn dưới dạng véc tơ: \(\vec F + {\vec F_{ms}} + \vec P + \vec N = m.\overrightarrow a \) (1) - Chiếu (1) lên trục Ox, Oy ta được: \(\left\{ \begin{array}{l}F--{F_{ms}} = ma\\ - P + N = 0\;\end{array} \right. \Rightarrow \left\{ \begin{array}{l}a = \dfrac{{F--{F_{ms}}}}{m}\\P = N\end{array} \right.\) Có: \({F_{ms}} = {\mu _t}.N = {\mu _t}.P = {\mu _t}.mg\) → Gia tốc chuyển động của vật: \(a = \dfrac{{F - {F_{ms}}}}{m} = \dfrac{{F - {\mu _t}.mg}}{m} = \dfrac{{4,5 - 0,2.1,5.10}}{{1,5}} = 1m/{s^2}\) b) Công thức xác định vận tốc: \(v = {v_0} + at = 0 + 1.t = t\,\,\left( {m/s} \right)\) Với \(t = 2s \Rightarrow v = 2\,\,\left( {m/s} \right)\) Câu hỏi 32 : Một vật có khối lượng m = 10kg đang đứng yên trên mặt phẳng nằm ngang. Biết hệ số ma sát trượt giữa vật và sàn là μ = 0,1. Lấy g =10m/s2. Tác dụng một lực kéo F =30N theo phương ngang vào vật. a, Xác định gia tốc và vận tốc của vật sau 5 giây. b, Sau 5 giây thì lực F ngừng tác dụng. Xác định thời gian và quãng đường mà vật đi được kể từ khi lực F ngừng tác dụng. c, Sau 5 giây kể từ khi vật bắt đầu chuyển động, tác dụng thêm lực F1 = 45N vào vật và có hướng ngược với hướng chuyển động của vật. Xác định quãng đường mà vật đi được trong 5 giây kể từ khi có thêm lực F1 Phương pháp giải: Động lực học chất điểm Lời giải chi tiết: Ta có hình vẽ: Chọn hệ trục tọa độ Oxy như hình . Các lực tác dụng vào vật gồm : \(\overrightarrow N ,\overrightarrow P ,\overrightarrow F ,\overrightarrow {{F_{ms}}} \) Áp dụng định luật II Niu- tơn. \(\overrightarrow N + \overrightarrow P + \overrightarrow F + \overrightarrow {{F_{ms}}} = m.\overrightarrow a \) Chiếu lên hai trục Ox và Oy ta có: \(\begin{array}{l} Phương trình vận tốc là: v = v0 + at = at => v5 = 2.5 = 10 m/s2 b) Khi ngừng tác dụng lực thì các lực tác dụng lên vật là \(\overrightarrow N ,\overrightarrow P ,\overrightarrow {{F_{ms}}} \) Áp dụng định luật II Niu- tơn. \(\overrightarrow N + \overrightarrow P + \overrightarrow {{F_{ms}}} = m.\overrightarrow {a'} \) Chiếu lên hai trục Ox và Oy ta có: \(\begin{array}{l} Vậy từ sau 5s thì vật chuyển động chậm dần đều với gia tốc – 1 m/s2 Phương trình vận tốc là v = v5 + a’t = 10 – t Đến khi vật dừng lại thì v = 0 nên ta có: 10 – t = 0 => t = 10s Áp dụng công thức độc lập với thời gian ta có: v2 – v52 = 2.a’.s => \(s = \frac{{0 - {{10}^2}}}{{2.( - 1)}} = 50m\) Quãng đường vật đi được từ khi ngừng tác dụng lực F là 50m. c) Sau 5s thì vật có vận tốc 10 m/s. Vật chịu thêm tác dụng lực F1. Các lực tác dụng vào vật gồm : \(\overrightarrow N ,\overrightarrow P ,\overrightarrow F ,\overrightarrow {{F_{ms}}} ,\overrightarrow {{F_1}} \) Áp dụng định luật II Niu- tơn. \(\overrightarrow N + \overrightarrow P + \overrightarrow F + \overrightarrow {{F_{ms}}} + \overrightarrow {{F_1}} = m.\overrightarrow a \) Chiếu lên hai trục Ox và Oy ta có: \(\begin{array}{l} Phương trình vận tốc là: v = v0 + a2 t = 10 – 2,5.t . Vật dừng lại sau thời gian là: 10 – 2,5 t = 0 => t = 4s. Vậy sau đó vật đổi chiều chuyển động. Trong thời gian 5s sau khi tác dụng lực F1 thì vật chuyển động qua hai giai đoạn: giai đoạn chuyển động cùng chiều Ox chậm dần đều trong 4s đầu, sau đó đổi chiều chuyển động ngược với Ox với gia tốc 2,5 m/s2. Quãng đường trong 4s đầu tiên là: \({S_1} = \frac{{0 - {{10}^2}}}{{2.( - 2,5)}} = 20m\) Quãng đường đi được trong 1s sau là: \({S_2} = \frac{1}{2}.a_2^2.{t^2} = \frac{1}{2}.2,{5^2}.1 = 3,125m\) Vậy quãng đường tổng cộng vật đi được là S = S1 + S2 = 20 + 3,125 = 23,125 (m) Câu hỏi 33 : Một vật khối lượng m = 5 kg, đang nằm yên thì chuyển động nhanh dần đều trên mặt phẳng ngang nhờ một lực kéo F theo phương ngang có độ lớn không đổi. Sau khi đi được 8 m, vật đạt vận tốc 14,4 km/h. Biết hệ số ma sát giữa vật và mặt phẳng ngang là µ = 0,2 và lấy g = 10 m/s2 . a. Tính độ lớn của lực kéo F r . b. Ngay khi vật đạt vận tốc 14,4 km/h, lực kéo F ngừng tác dụng, theo quán tính vật tiếp tục chuyển động lên mặt phẳng nghiêng có góc nghiêng α = 150 so với phương ngang. Biết hệ số ma sát giữa vật và mặt phẳng nghiêng là 0,1. Tính độ cao lớn nhất mà vật đạt được trên mặt phẳng nghiêng.
Đáp án: A Phương pháp giải: : a) Dùng phương trình độc lập với thời gian : \({v^2} - v_0^2 = 2as\) để tìm gia tốc a. Vẽ hình biểu diễn các lực tác dụng lên xe trên hệ trục tọa độ Oxy: lực của động cơ, lực ma sát, trọng lực, phản lực N. Dùng định luật II Niu – Tơn: \(\sum {\overrightarrow F } = m.\overrightarrow a \) . Sau đó chiếu phương trình định luật II lên các trục tọa độ. Và tìm F. b) Khi lực F ngừng tác dụng, chỉ còn lực ma sát, trọng lực và phản lực. Vẽ hình vật trên mặt phẳng nghiêng, Dùng định luật II Niu – Tơn: \(\sum {\overrightarrow F } = m.\overrightarrow a \) . Sau đó chiếu phương trình định luật II lên các trục tọa độ. Và tìm gia tốc mới. Dùng phương trình độc lập với thời gian : \({v^2} - v_0^2 = 2as\) để tìm quãng đường vật đi được đến khi dừng lại. Sau đó tìm độ cao vật đạt được h = s.sinα Lời giải chi tiết: Đổi 14,4 km/h = 4m/s. Gia tốc a của vật là \({v^2} - v_0^2 = 2as \Leftrightarrow a = \frac{{{4^2} - 0}}{{2.8}} = 1m/{s^2}\) Ta có hình vẽ Chọn hệ quy chiếu gắn với mặt đất, các lực tác dụng lên vật như trên hình vẽ Vật chuyển động thẳng với gia tốc = 1 m/s2, theo định luật I và II Niu – tơn ta có \(\overrightarrow F + \overrightarrow P + \overrightarrow N + \overrightarrow {{F_{ms}}} = m.\overrightarrow a \) Chiếu lên hai trục Ox, Oy ta được \(\left\{ \begin{array}{l} Vậy lực của động cơ là 15 N b) Bây giờ vật chuyển động trên mặt phẳng nghiêng Ta có hình vẽ \(\overrightarrow P + \overrightarrow N + \overrightarrow {{F_{ms}}} = m.\overrightarrow {a'} \) Chiếu lên hai trục Ox, Oy ta được \(\begin{array}{l} Vậy xe chuyển động chậm dần đều với gia tốc a = -3,55 m/s2. Quãng đường xe đi được đến khi dừng lại là s, được xác định bởi \(\begin{array}{l} Vậy vật đi được 2,25 m trước khi dừng hẳn; Độ cao mà vật đạt được là \(h = s.\sin {15^0} = 2,25.\sin {15^0} = 0,58m\) Câu hỏi 34 : Một vật có m = 2kg trượt không vận tốc ban đầu trên mặt phẳng nghiêng nhẵn, dài 10m, chiều cao 5m. Lấy g = 10m/s2 ; hệ số ma sát trên mặt phẳng nghiêng là µ1 = 0,25. a) Tính gia tốc của vật trên mặt phẳng nghiêng và vận tốc của vật tại chân mặt phẳng nghiêng. b) Khi xuống hết mặt phẳng nghiêng, vật tiếp tục chuyển động trên mặt phẳng ngang, hệ số ma sát là µ2 = 0,5. Tính quãng đường từ lúc vật bắt đầu chuyển động trên mặt phẳng ngang cho đến khi dừng hẳn.
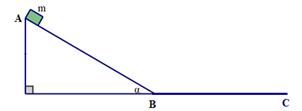
Đáp án: A Phương pháp giải: Phương pháp động lực học: Bước 1: Chọn vật (hệ vật) khảo sát. Bước 2: Chọn hệ quy chiếu (Cụ thể hoá bằng hệ trục toạ độ vuông góc; Trục toạ độ Ox luôn trùng với phương chiều chuyển động; Trục toạ độ Oy vuông góc với phương chuyển động) Bước 3: Xác định các lực và biểu diễn các lực tác dụng lên vật trên hình vẽ. Bước 4: Viết phương trình hợp lực tác dụng lên vật theo định luật II Niu Tơn. \(\overrightarrow {{F_{hl}}} = \overrightarrow {{F_1}} + \overrightarrow {{F_2}} + ... + \overrightarrow {{F_n}} = m.\overrightarrow a \) (*) (Tổng tất cả các lực tác dụng lên vật) Bước 5: Chiếu phương trình lực (*) lên các trục toạ độ Ox, Oy: Ox: F1x + F2x + … + Fnx = ma (1) Oy: F1y + F2y + … + Fny = 0 (2) Giải phương trình (1) và (2) ta thu được đại lượng cần tìm Lời giải chi tiết: m = 2kg ; v0 = 0 ; s1 = 10m ; h = 5m ; g = 10m/s2; µ1 = 0,25; µ2 = 0,5. a) Ta có: \(\sin \alpha = \dfrac{h}{{{s_1}}} = \dfrac{5}{{10}} = \dfrac{1}{2} \Rightarrow \alpha = {30^0}\) Các lực tác dụng vào vật khi vật chuyển động trên mặt phẳng nghiêng: \(\overrightarrow P ;\overrightarrow {{F_{ms1}}} ;\overrightarrow {{N_1}} \) Áp dụng định luật II Niu tơn ta có: \(\overrightarrow P + \overrightarrow {{F_{ms1}}} + \overrightarrow {{N_1}} = m\overrightarrow {{a_1}} \,\,\,\,\,\left( 1 \right)\) Chiếu (1) lên Ox và Oy ta có: \(\begin{array}{l}\left\{ \begin{array}{l}P.sin\alpha - {F_{ms1}} = m{a_1}\\ - {\rm{ }}Pcos\alpha + N = 0\end{array} \right. \Rightarrow \left\{ \begin{array}{l}N = P.\cos \alpha \Rightarrow {F_{ms1}} = {\mu _1}P.\cos \alpha \\P.sin\alpha - {F_{ms1}} = m{a_1}\,\end{array} \right.\\ \Rightarrow mg.sin\alpha - {\mu _1}mg.\cos \alpha = m{a_1}\\ \Rightarrow {a_1} = g.\left( {sin\alpha - {\mu _1}\cos \alpha } \right) = 10.\left( {\sin 30 - 0,25.\cos 30} \right) \approx 2,835m/{s^2}\end{array}\) Vận tốc của vật tại chân mặt phẳng nghiêng: \(v_B^2 - v_A^2 = 2{a_1}{s_1} \Rightarrow {v_B} = \sqrt {2{a_1}.{s_1}} = \sqrt {2.2,835.10} = 7,53m/s\) b) Các lực tác dụng vào vật khi vật chuyển động trên mặt phẳng ngang: \(\overrightarrow P ;\overrightarrow {{F_{ms2}}} ;\overrightarrow {{N_2}} \) Áp dụng định luật II Niu tơn ta có: \(\overrightarrow P + \overrightarrow {{F_{ms2}}} + \overrightarrow {{N_2}} = m\overrightarrow {{a_2}} \,\,\,\,\,\left( 2 \right)\) Chiếu (2) lên trục Ox ta có: \( - {F_{ms2}} = m{a_2} \Rightarrow - {\mu _2}mg = m{a_2} \Rightarrow {a_2} = - {\mu _2}g = - 0,5.10 = - 5m/{s^2}\) Giả sử đến C vật dừng lại. Ta có : \(\begin{gathered} Chọn A. Câu hỏi 35 : Một sợi dây có chiều dài l = 40cm, một đầu được buộc vào điểm O cố định, đầu còn lại nối với vật M có khối lượng m. M đang đứng yên ở vị trí dây treo thẳng đứng thì một vật có khối lượng mo= 1/3 m chuyển động theo phương ngang với tốc độ vo va chạm với M. Xác định điều kiện về vo để sau va chạm hai vật dính và nhau và cùng chuyển động trên đường tròn tâm O trong mặt phẳng thẳng đứng. (Lấy g= 10m/s2 và bỏ qua sức cản của không khí). Phương pháp giải: Sau va chạm hai vật dính vào nhau, đây là va chạm mềm, ta áp dụng định luật bảo toàn động lượng cho hai vật, xác định được vận tốc sau va chạm của hai vật: \(\overrightarrow {{p_{tr}}} = \overrightarrow {{p_s}} \) Công thức liên hệ giữa gia tốc hướng tâm và vận tốc tiếp tuyến: \({a_{ht}} = \frac{{{v^2}}}{r}\) Theo định luật II Niu – Tơn thì: \(\overrightarrow T + \overrightarrow P = m.\overrightarrow {{a_{ht}}} \) Để hai vật chuyển động trên đường tròn tâm O trong mặt phẳng thẳng đứng thì tổng lực căng dây và trọng lực đóng vai trò lực hướng tâm. Lực căng dây tại vị trí cao nhất ≥ 0. Lời giải chi tiết: Tóm tắt: \(m;l = 40cm;{m_0} = \frac{1}{3}m;{v_0};g = 10m/{s^2}\) Tìm điều kiện của v0 để sau khi va chạm mềm hai vật chuyển động tròn đều quanh điểm treo dây O. Bài làm: Sau va chạm hai vật dính vào nhau, đây là va chạm mềm, ta áp dụng định luật bảo toàn động lượng cho hai vật: \(\overrightarrow {{p_{tr}}} = \overrightarrow {{p_s}} \) Ta có: \(\frac{1}{3}.m.{v_0} = \left( {m + \frac{1}{3}m} \right).v \Rightarrow v = \frac{{{v_0}}}{4}\) Gia tốc hướng tâm của hệ hai vật sau va chạm là: \({a_{ht}} = \frac{{{v^2}}}{r} = \frac{{v_0^2}}{{16.0,4}} = \frac{{v_0^2}}{{6,4}}\) Theo định luật II Niu – tơn ta có: \(\overrightarrow T + \overrightarrow P = m.\overrightarrow {{a_{ht}}} \) (*) Tại vị trí cao nhât, chiếu (*) lên phương bán kính ta có: \(\overrightarrow T + \overrightarrow P = m.\overrightarrow {{a_{ht}}} \) Tại vị trí cao nhât, chiếu (*) lên phương bán kính ta có: \(T + P = m.{a_{ht}} \Rightarrow T = m.{a_{ht}} - P\) Điều kiện là T tại vị trí cao nhất của quỹ đạo ≥ 0. Ta có: \(\begin{array}{l} Vậy điều kiện để sau va chạm hai vật chuyển động tròn đều quanh vị trí treo dây là \({v_0} \ge 8{\rm{ }}m/s\)
Quảng cáo
|