50 bài tập Định luật Ôm đối với toàn mạch mức độ vận dụng (Phần 2)Làm bàiQuảng cáo
Câu hỏi 1 : Một nguồn có E = 3V, r = 1Ω nối với điện trở ngoài R = 2Ω thành mạch điện kín. Công suất của nguồn điện là:
Đáp án: A Phương pháp giải: Hệ thức định luật Ôm: \(I = \frac{E}{{R + r}}\) Công suất của nguồn: \({P_{ng}} = E.I\) Lời giải chi tiết: Công suất của nguồn điện: \(P = E.I = E.\frac{E}{{r + R}} = \frac{{3{}^2}}{{1 + 2}} = 3W\) Chọn A. Câu hỏi 2 : Một mạch điện kín gồm bộ nguồn có hai pin giống nhau mắc nối tiếp, mỗi pin có suất điện động 3V, điện trở trong bằng 1Ω và mạch ngoài là một điện trở R = 2Ω. Hiệu điện thế giữa hai cực của mỗi pin là
Đáp án: B Phương pháp giải: Áp dụng công thức định luật Ôm \(I = \frac{{{E_b}}}{{r + R}}\) Hiệu điện thế hai đầu nguồn điện là \(U = E - I.r\) Lời giải chi tiết: Cường độ dòng điện chạy trong mạch: \(I = \frac{{{E_b}}}{{{r_b} + R}} = \frac{6}{{2 + 2}} = 1,5A\) Hiệu điện thế hai cực của mỗi pin: \(U = E - I.r = 3 - 1,5.1 = 1,5V\) Chọn B. Câu hỏi 3 : Mạch điện gồm điện trở \(R = 5\,\,\Omega \) mắc thành mạch điện kín với nguồn có suất điện động \(3\,\,V\) và điện trở trong \(r = 1\,\,\Omega \) thì cường độ dòng điện trong mạch có giá trị là
Đáp án: C Phương pháp giải: Định luật Ôm cho mạch điện: \(I = \dfrac{E}{{R + r}}\) Lời giải chi tiết: Cường độ dòng điện trong mạch là: \(I = \dfrac{E}{{R + r}} = \dfrac{3}{{5 + 1}} = 0,5\,\,\left( A \right)\) Chọn C. Câu hỏi 4 : Một mạch điện kín gồm nguồn điện \(E = 12\,\,V;\,\,r = 1\,\,\Omega \). Mạch ngoài gồm bóng đèn có ghi \(\left( {6V - 6W} \right)\) mắc nối tiếp với một biến trở. Để đèn sáng bình thường, biến trở có giá trị bằng
Đáp án: C Phương pháp giải: Cường độ dòng điện trong mạch: \(I = \dfrac{E}{{R + {R_d} + r}}\) Đèn sáng bình thường khi: \({I_d} = {I_{dm}}\) Lời giải chi tiết: Điện trở của đèn là: \({R_d} = \dfrac{{{U_{dm}}^2}}{{{P_{dm}}}} = \dfrac{{{6^2}}}{6} = 6\,\,\left( \Omega \right)\) Cường độ dòng điện định mức của đèn là: \({I_{dm}} = \dfrac{{{P_{dm}}}}{{{U_{dm}}}} = \dfrac{6}{6} = 1\,\,\left( A \right)\) Cường độ dòng điện trong mạch là: \(I = \dfrac{E}{{R + {R_d} + r}}\) Để đèn sáng bình thường, ta có: \(I = {I_{dm}} \Rightarrow \dfrac{E}{{R + {R_d} + r}} = {I_{dm}} \Rightarrow \dfrac{{12}}{{R + 6 + 1}} = 1 \Rightarrow R = 5\,\,\left( \Omega \right)\) Chọn C. Câu hỏi 5 : Một mạch điện kín gồm nguồn điện có suất điện động E, điện trở trong r = 5Ω. Mạch ngoài là một điện trở R = 20 Ω. Hiệu suất của nguồn là
Đáp án: A Phương pháp giải: Hiệu suất của nguồn là: \(H = \frac{R}{{(r + R)}}.100\% \) Lời giải chi tiết: Hiệu suất của nguồn là: \(H = \frac{R}{{(r + R)}}.100\% = \frac{{20}}{{5 + 20}}.100\% = 80\% \) Chọn A. Câu hỏi 6 : Mắc điện trở R = 2 Ω vào hai cực của nguồn điện không đổi có suất điện động E = 6 V, điện trở trong r = 1 Ω. Công suất tiêu thụ ở mạch ngoài có giá trị
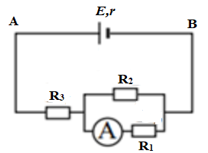
Đáp án: D Phương pháp giải: Áp dụng định luật Ôm cho toàn mạch: \(I = \frac{E}{{R + r}}\) Công suất tiêu thụ mạch ngoài: \(P = {I^2}.R = \frac{{{E^2}}}{{{{(R + r)}^2}}}.R\) Lời giải chi tiết: Công suất tiêu thụ ở mạch ngoài: \(P = {I^2}.R = \frac{{{E^2}}}{{{{(R + r)}^2}}}.R = \frac{{{6^2}}}{{{{(2 + 1)}^2}}}.2 = 8{\rm{W}}\) Chọn D. Câu hỏi 7 : Cho mạch điện có sơ đồ như hình vẽ: \(E = 8V\), \(r = 1,0\Omega \); \({R_1} = 12\Omega \); \({R_2} = 6\Omega \). Bỏ qua điện trở của ampe kế và dây nối. Số chỉ của ampe kế là \(0,33 \approx \dfrac{1}{3}A\). Nhiệt lượng tỏa ra trên \({R_3}\) trong 10 phút là
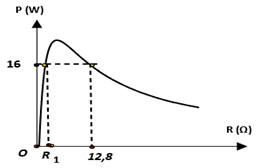
Đáp án: B Phương pháp giải: + Sử dụng biểu thức của đoạn mạch mắc song song, nối tiếp + Sử dụng biểu thức định luật ôm cho toàn mạch: \(I = \dfrac{E}{{{R_N} + r}}\) + Sử dụng biểu thức tính nhiệt lượng tỏa ra: \(Q = {I^2}Rt\) Lời giải chi tiết: + \({I_A} = {I_1} = \dfrac{1}{3}A\) \( \Rightarrow {U_1} = {I_1}{R_1} = \dfrac{1}{3}.12 = 4V\) Lại có: \({U_{12}} = {U_1} = {U_2}\) \({I_{12}} = I = \dfrac{{{U_{12}}}}{{{R_{12}}}}\) và \({R_{12}} = \dfrac{{{R_1}{R_2}}}{{{R_1} + {R_2}}} = 4\Omega \) \( \Rightarrow I = \dfrac{4}{4} = 1A\) Mặt khác: + Điện trở mạch ngoài: \({R_N} = \dfrac{{{R_1}{R_2}}}{{{R_1} + {R_2}}} + {R_3} = 7\Omega \Rightarrow {R_3} = 3\Omega \) Nhiệt lượng tỏa ra trên \({R_3}\) trong \(t = 10' = 600s\) là: \(Q = {I^2}.{R_3}t = {1^2}.3.600 = 1800J = 1,8kJ\) Chọn B Câu hỏi 8 : Một mạch điện kín gồm một biến trở thuần \(R,\) nguồn điện không đổi có suất điện động \(E,\) điện trở trong \(r = 8\Omega \). Đồ thị biểu diễn sự phụ thuộc của công suất tiêu thụ trên biến trở theo \(R\) như hình vẽ bên. Giá trị của \(R_1\) là
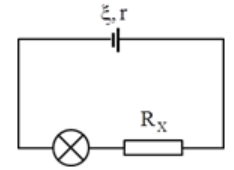
Đáp án: D Phương pháp giải: Định luật Ôm: \(I = \dfrac{E}{{r + R}}\) Công suất tiêu thụ trên biến trở: \(P = {I^2}R\) Lời giải chi tiết: Công suất tiêu thụ trên biến trở: \(P = {I^2}R = {\left( {\dfrac{E}{{r + R}}} \right)^2}.R\) Từ đồ thị ta thấy khi \(R = {R_1}\) và \(R = 12,8\Omega \) thì công suất tiêu thụ trên biến trở có cùng giá trị. Ta có: \(\begin{array}{l}{\left( {\dfrac{E}{{8 + {R_1}}}} \right)^2}.{R_1} = {\left( {\dfrac{E}{{8 + 12,8}}} \right)^2}.12,8\\ \Leftrightarrow \dfrac{{{R_1}}}{{{{\left( {8 + {R_1}} \right)}^2}}} = \dfrac{{12,8}}{{{{\left( {8 + 12,8} \right)}^2}}} \Rightarrow {R_1} = 5\Omega \end{array}\) Chọn D. Câu hỏi 9 : Cho mạch điện như hình vẽ. Biết \(E = 12\,\,V,\,\,r = 4\,\,\Omega \), bóng đèn thuộc loại \(6\,\,V - 6\,\,W\). Để đèn sáng bình thường thì giá trị của \({R_x}\) là
Đáp án: C Phương pháp giải: Điện trở của đèn: \({R_d} = \dfrac{{{U_{dm}}^2}}{{{P_{dm}}}}\) Cường độ dòng điện trong mạch: \(I = \dfrac{E}{{r + {R_d} + {R_x}}}\) Điều kiện để đèn sáng bình thường: \(I = {I_{dm}}\) Lời giải chi tiết: Cường độ dòng điện định mức của đèn là: \({I_{dm}} = \dfrac{{{P_{dm}}}}{{{U_{dm}}}} = \dfrac{6}{6} = 1\,\,\left( A \right)\) Điện trở của đèn là: \({R_d} = \dfrac{{{U_d}^2}}{{{P_d}}} = \dfrac{{{6^2}}}{6} = 6\,\,\left( \Omega \right)\) Cường độ dòng điện qua đèn là: \(I = \dfrac{E}{{r + {R_d} + {R_x}}}\) Để đèn sáng bình thường, ta có: \(I = {I_{dm}} \Rightarrow \dfrac{E}{{r + {R_d} + {R_x}}} = {I_{dm}} \Rightarrow \dfrac{{12}}{{4 + 6 + {R_x}}} = 1 \Rightarrow {R_x} = 2\,\,\left( \Omega \right)\) Chọn C. Câu hỏi 10 : Một nguồn điện có suất điện động E = 6 V, điện trở trong r = 1 Ω, mạch ngoài chỉ có biến trở R. Để công suất tiêu thụ ở mạch ngoài là 9 W thì biến trở R phải có giá trị
Đáp án: D Phương pháp giải: Biểu thức định luật Ôm cho toàn mạch: \(I=\frac{E}{r+R}\) Công suất tiêu thụ điện: \(P={{I}^{2}}R\) Lời giải chi tiết: Cường độ dòng điện mạch chính là: \(I=\frac{E}{r+R}=\frac{6}{1+R}\) Công suất tiêu thụ ở mạch ngoài là: \(P={{I}^{2}}R\Rightarrow 9=\frac{{{6}^{2}}}{{{(1+R)}^{2}}}\Rightarrow R=1\Omega \) Chọn D. Câu hỏi 11 : Nguồn điện có \(r = 0,2\Omega \), mắc với \(R = 2,4\Omega \) thành mạch kín, khi đó hiệu điện thế giữa hai đầu R là 12 V. Suất điện động của nguồn là
Đáp án: C Phương pháp giải: Vận dụng biểu thức định luật ôm cho toàn mạch: \(I = \dfrac{E}{{R + r}}\) Lời giải chi tiết: Ta có: \(I = \dfrac{E}{{R + r}}\) Hiệu điện thế giữa hai đầu R: \(U = I.R \Leftrightarrow U = \dfrac{E}{{R + r}}.R\) \(\begin{array}{l} \Leftrightarrow 12 = \dfrac{E}{{2,4 + 0,2}}.2,4\\ \Rightarrow E = 13V\end{array}\) Chọn C Câu hỏi 12 : Biến trở \({R_x}\) mắc vào hai cực của nguồn điện có suất điện động \(E\) và điện trở trong \(r\). Điều chỉnh biến trở để công suất tỏa nhiệt của dòng điện qua nó đạt cực đại. Giá trị của công suất cực đại là
Đáp án: D Phương pháp giải: Định luật Ôm cho toàn mạch: \(I = \dfrac{E}{{R + r}}\) Công suất: \(P = {I^2}R\) Áp dụng bất đẳng thức Cô - si Lời giải chi tiết: Cường độ dòng điện qua mạch là: \(I = \dfrac{E}{{{R_x} + r}}\) Công suất tỏa nhiệt trên biến trở là: \(P = {I^2}R = \dfrac{{{E^2}}}{{{{\left( {{R_x} + r} \right)}^2}}}{R_x} = \dfrac{{{E^2}}}{{{{\left( {\sqrt {{R_x}} + \dfrac{r}{{\sqrt {{R_x}} }}} \right)}^2}}}\) Để \({P_{max}}\) thì \(\left( {\sqrt R + \dfrac{r}{{\sqrt R }}} \right)\) nhỏ nhất. Áp dụng bất đẳng thức Cô - si, ta có: \(\left( {\sqrt {{R_x}} + \dfrac{r}{{\sqrt {{R_x}} }}} \right) \ge 2\sqrt r \) Dấu “=” xảy ra khi \(\sqrt {{R_x}} \, = \,\dfrac{r}{{\sqrt {{R_x}} }}\,\, \Rightarrow \,{R_x}\, = \,r\) Khi đó: \({P_{max}} = \dfrac{{{E^2}}}{{4r}} = \dfrac{{{E^2}}}{{4{R_x}}}\) Chọn D. Câu hỏi 13 : Một nguồn điện có suất điện động bằng \(3\,\,V\), điện trở trong \(1\,\,\Omega \). Mắc vào hai cực của nguồn điện một biến trở \(R\). Điều chỉnh giá trị của \(R\) để công suất mạch ngoài đạt cực đại. Khi đó hiệu điện thế giữa hai cực của nguồn điện là
Đáp án: C Phương pháp giải: Công suất của mạch ngoài: \(P = {I^2}.R = \frac{{{E^2}R}}{{{{(R + r)}^2}}} = \frac{{{E^2}}}{{R + 2r + \frac{{{r^2}}}{R}}} = \frac{{{E^2}}}{{2r + R + \frac{{{r^2}}}{R}}}\) Định luật Ôm cho toàn mạch: \(I = \frac{E}{{r + R}}\) Hiệu điện thế giữa hai cực của nguồn: \(U = I.R = E-I.r\) Lời giải chi tiết: Công suất tiêu thụ của mạch ngoài là: \(P = {I^2}.R = \frac{{{E^2}R}}{{{{(R + r)}^2}}} = \frac{{{E^2}}}{{R + 2r + \frac{{{r^2}}}{R}}} = \frac{{{E^2}}}{{2r + R + \frac{{{r^2}}}{R}}}\) Để công suất tiêu thụ cực đại thì \(\left( {2r + R + \frac{{{r^2}}}{R}} \right)\) phải nhỏ nhất. Áp dụng bất đẳng thức Cosi ta có: \(R + \frac{{{r^2}}}{R} \ge 2r\) Vậy mẫu số nhỏ nhất khi: \(R = \frac{{{r^2}}}{R} \Leftrightarrow R = r = 1\Omega \) Áp dụng định luật Ôm cho toàn mạch, ta có: \(I = \frac{E}{{r + R}} = \frac{3}{{1 + 1}} = 1,5A\) Hiệu điện thế giữa hai cực của nguồn là: \(U = I.R = E-I.r = 3-1,5.1 = 1,5V\) Chọn C. Câu hỏi 14 : Một điện trở \({R_1}\) được mắc vào hai cực của một nguồn điện có điện trở trong \(r = 4\Omega \) thì dòng điện chạy trong mạch có cường độ là \({I_1} = 1,2A\). Nếu mắc thêm một điện trở \({R_2} = 2\Omega \) nối tiếp với điện trở \({R_1}\) thì dòng điện chạy trong mạch chính có cường độ là \({I_2} = 1A\). Trị số của điện trở \({R_1}\) là
Đáp án: A Phương pháp giải: Sử dụng biểu thức định luật ôm cho toàn mạch: \(I = \dfrac{E}{{R + r}}\) Lời giải chi tiết: Ta có: + Khi mắc \({R_1}\): \({I_1} = \dfrac{E}{{{R_1} + r}}\) (1) + Khi mắc thêm \({R_2}nt{R_1}\): \({I_2} = \dfrac{E}{{{R_N} + r}} = \dfrac{E}{{{R_1} + {R_2} + r}}\) (2) Lấy \(\dfrac{{\left( 1 \right)}}{{\left( 2 \right)}}\) ta được: \(\dfrac{{{I_1}}}{{{I_2}}} = \dfrac{{{R_1} + {R_2} + r}}{{{R_1} + r}}\) \(\begin{array}{l} \Leftrightarrow \dfrac{{1,2}}{1} = \dfrac{{{R_1} + 2 + 4}}{{{R_1} + 4}}\\ \Rightarrow {R_1} = 6\Omega \end{array}\) Chọn A Câu hỏi 15 : Một điện trở R = 5,8Ω được mắc vào hai cực của một nguồn điện một chiều có suất điện động x = 9V và điện trở trong r = 0,2Ω thành mạch điện kín. Bỏ qua điện trở của dây nối. Công suất tiêu thụ của mạch ngoài là
Đáp án: D Phương pháp giải: Định luật Ôm cho toàn mạch: \(I = \dfrac{\xi }{{R + r}}\) Công suất tiêu thụ của mạch ngoài: \(P = {I^2}R\) Lời giải chi tiết: Cường độ dòng điện chạy trong mạch: \(I = \dfrac{\xi }{{R + r}} = \dfrac{9}{{5,8 + 0,2}} = 1,5A\) Công suất tiêu thụ của mạch ngoài: \(P = {I^2}R = 1,{5^2}.5,8 = 13,05W\) Chọn D. Câu hỏi 16 : Một điện trở R = 3,6Ω được mắc vào hai cực của một nguồn điện một chiều có suất điện động \(\xi = 8V\)và điện trở trong r = 0,4Ω thành mạch điện kín. Bỏ qua điện trở của dây nối. Công suất của nguồn điện là
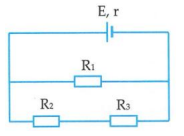
Đáp án: D Phương pháp giải: Công suất của nguồn điện : \(P = \xi .I\) Trong đó : \(I = \dfrac{\xi }{{R + r}}\) Lời giải chi tiết: Cường độ dòng điện chạy trong mạch : \(I = \dfrac{\xi }{{R + r}} = \dfrac{8}{{3,6 + 0,4}} = 2A\) Công suất của nguồn điện : \(P = \xi .I = 8.2 = 16W\) Chọn D. Câu hỏi 17 : Cho mạch điện kín gồm nguồn điện có suất điện động \(E = 12V\), điện trở trong \(r = 2\Omega \) nối với mạch ngoài gồm điện trở \({R_1} = 6\Omega ,{R_2} = 4\Omega ,{R_3} = 8\Omega \) mắc theo sơ đồ như hình vẽ. Điện trở các dây nối không đáng kể. Cường độ dòng điện qua R2 xấp xỉ bằng
Đáp án: D Phương pháp giải: + Sử dụng biểu thức xác định điện trở của mạch có các điện trở mắc nối tiếp và song song. + Áp dụng biểu thức định luật ôm cho toàn mạch: \(I = \dfrac{E}{{{R_N} + r}}\) Lời giải chi tiết: Ta có mạch ngoài gồm \(\left( {{R_2}nt{R_3}} \right)//{R_1}\) \({R_{23}} = {R_2} + {R_3} = 4 + 8 = 12\Omega \) \({R_N} = \dfrac{{{R_{23}}{R_1}}}{{{R_{23}} + {R_1}}} = \dfrac{{12.6}}{{12 + 6}} = 4\Omega \) Cường độ dòng điện qua mạch: \(I = \dfrac{E}{{{R_N} + r}} = \dfrac{{12}}{{4 + 2}} = 2A\) Hiệu điện thế mạch ngoài: \({U_N} = I.{R_N} = 2.4 = 8V\) Lại có: \({U_1} = {U_{23}} = {U_N}\) \( \Rightarrow {I_{23}} = \dfrac{{{U_{23}}}}{{{R_{23}}}} = \dfrac{{{U_N}}}{{{R_{23}}}} = \dfrac{8}{{12}} = 0,67A\) Cường độ dòng điện qua \({R_2}\) là \({I_2} = {I_{23}} = 0,67A\) Chọn D Câu hỏi 18 : Một bóng đèn có ghi 6V – 3W, một điện trở R và một nguồn điện được mắc thành mạch kín như hình vẽ. Biết nguồn điện có suất điện động E = 12V và điện trở trong r = 2Ω; đèn sáng bình thường. Giá trị của R là:
Đáp án: D Phương pháp giải: Áp dụng công thức tính điện trở của đèn: \({{R}_{d}}=\frac{{{U}_{dm}}^{2}}{{{P}_{dm}}}\) Để đèn sáng bình thường thì cường độ dòng điện qua đèn phải bằng giá trị định mức: \({{I}_{dm}}=\frac{{{P}_{dm}}}{{{U}_{dm}}}\) Đoạn mạch điện trong sơ đồ gồm đèn và điện trở R mắc nối tiếp. Áp dụng định luật Ôm cho toàn mạch ta có: \(I=\frac{E}{{{R}_{d}}+R+r}\) Lời giải chi tiết: Điện trở của đèn: \({{R}_{d}}=\frac{{{U}_{dm}}^{2}}{{{P}_{dm}}}=\frac{{{6}^{2}}}{3}={{12}_{{}}}\Omega \) Để đèn sáng bình thường thì cường độ dòng điện qua đèn phải bằng giá trị định mức: \(I={{I}_{dm}}=\frac{{{P}_{dm}}}{{{U}_{dm}}}=\frac{3}{6}=0,5A\) Đoạn mạch điện trong sơ đồ gồm đèn và điện trở R mắc nối tiếp. Áp dụng định luật Ôm cho toàn mạch ta có: \(I=\frac{E}{{{R}_{d}}+R+r}\Rightarrow 0,5=\frac{12}{12+R+2}\Rightarrow R=10\Omega \) Chọn D. Câu hỏi 19 : Xét mạch điện kín đơn giản gồm một nguồn điện có \(\varepsilon =12\,\,V\), điện trở trong r và mạch ngoài có một điện trở \(R=6,5\,\,\Omega \). Biết cường độ dòng điện trong mạch là 1,5 A. Xác định r.
Đáp án: D Phương pháp giải: Định luật Ôm cho toàn mạch: \(I=\frac{\varepsilon }{r+R}\) Lời giải chi tiết: Cường độ dòng điện trong mạch là: \(I=\frac{\varepsilon }{r+R}\Rightarrow 1,5=\frac{12}{r+6,5}\Rightarrow r=1,5\,\,\left( \Omega \right)\) Chọn D. Câu hỏi 20 : Một mạch điện kín gồm nguồn điện có suất điện động là E, điện trở trong \(r = 4\Omega \). Mạch ngoài là một điện trở \(R = 20\Omega \). Biết cường độ dòng điện trong mạch là \(I = 0,5A\) . Suất điện động của nguồn là
Đáp án: A Phương pháp giải: Sử dụng biểu thức định luật Ôm cho toàn mạch: \(I = \dfrac{E}{{R + r}}\) Lời giải chi tiết: Ta có, cường độ dòng điện trong mạch: \(I = \dfrac{E}{{R + r}}\) \(\begin{array}{l} \Leftrightarrow 0,5 = \dfrac{E}{{20 + 4}}\\ \Rightarrow E = 12V\end{array}\) Chọn A Câu hỏi 21 : Một bóng đèn có ghi 6V – 3W, một điện trở R và một nguồn điện được mắc thành mạch kín như hình vẽ. Biết nguồn điện có suất điện động E = 12V và điện trở trong r = 2Ω; đèn sáng bình thường. Giá trị của R là:
Đáp án: D Phương pháp giải: Áp dụng công thức tính điện trở của đèn: \({R_d} = \frac{{{U_{dm}}^2}}{{{P_{dm}}}}\) Để đèn sáng bình thường thì cường độ dòng điện qua đèn phải bằng giá trị định mức: \({I_{dm}} = \frac{{{P_{dm}}}}{{{U_{dm}}}}\) Đoạn mạch điện trong sơ đồ gồm đèn và điện trở R mắc nối tiếp. Áp dụng định luật Ôm cho toàn mạch ta có: \(I = \frac{E}{{{R_d} + R + r}}\) Lời giải chi tiết: Điện trở của đèn: \({R_d} = \frac{{{U_{dm}}^2}}{{{P_{dm}}}} = \frac{{{6^2}}}{3} = {12_{}}\Omega \) Để đèn sáng bình thường thì cường độ dòng điện qua đèn phải bằng giá trị định mức: \(I = {I_{dm}} = \frac{{{P_{dm}}}}{{{U_{dm}}}} = \frac{3}{6} = 0,5A\) Đoạn mạch điện trong sơ đồ gồm đèn và điện trở R mắc nối tiếp. Áp dụng định luật Ôm cho toàn mạch ta có: \(I = \frac{E}{{{R_d} + R + r}} \Rightarrow 0,5 = \frac{{12}}{{12 + R + 2}} \Rightarrow R = 10\Omega \) Chọn D. Câu hỏi 22 : Một nguồn điện một chiều có suất điện động là 10 V và điện trở trong là 1 Ω. Nếu nối hai cực của nguồn điện bằng một dây dẫn có điện trở 4 Ω để tạo thành mạch điện kín thì cường độ dòng điện trong mạch là
Đáp án: C Phương pháp giải: Cường độ dòng điện trong mạch: \(I = \dfrac{E}{{r + R}}\) Lời giải chi tiết: Cường độ dòng điện trong mạch là: \(I = \dfrac{E}{{r + R}} = \dfrac{{10}}{{1 + 4}} = 2\,\,\left( A \right)\) Chọn C. Câu hỏi 23 : Cho mạch điện như hình vẽ. Biết \(E = 12V;r = 1\Omega ;{R_1} = 5\Omega ;{R_2} = {R_3} = 10\Omega \). Bỏ qua điện trở của dây nối. Hiệu điện thế giữa hai đầu R1 là
Đáp án: C Phương pháp giải: Áp dụng định luật Ôm tính cường độ dòng điện chạy trong mạch: \(I = \dfrac{E}{{r + {R_N}}}\) Sử dụng các công thức của đoạn mạch nối tiếp và song song. Hiệu điện thế hai đầu mạch ngoài: \(U = E - I.r\) Lời giải chi tiết: Mạch ngoài gồm: \({R_1}\,//\,\left( {{R_2}\,nt\,{R_3}} \right)\) Điện trở tương đương của mạch ngoài: \(\begin{array}{l}\dfrac{1}{{{R_N}}} = \dfrac{1}{{{R_1}}} + \dfrac{1}{{{R_{23}}}} = \dfrac{1}{{{R_1}}} + \dfrac{1}{{{R_2} + {R_3}}} = \dfrac{1}{5} + \dfrac{1}{{20}} = \dfrac{1}{4}\\ \Rightarrow {R_N} = 4\Omega \end{array}\) Cường độ dòng điện chạy trong mạch: \(I = \dfrac{E}{{r + {R_N}}} = \dfrac{{12}}{{1 + 4}} = 2,4A\) Hiệu điện thế giữa hai đầu R1 là \({U_1} = U = E - I.r = 12 - 2,4.1 = 9,6V\) Chọn C. Câu hỏi 24 : Cho mạch điện như hình vẽ. Biết E = 12V, r = 4Ω; bóng đèn thuộc loại 6V – 6W. Để đèn sáng bình thường thì giá trị của Rx là:
Đáp án: D Phương pháp giải: Điện trở của bóng đèn: \({R_d} = \dfrac{{U_d^2}}{{{P_d}}}\) Đèn sáng bình thường khi: \({I_d} = {I_{dm}} = \dfrac{{{P_d}}}{{{I_d}}}\) Cường độ dòng điện chạy trong mạch: \(I = \dfrac{E}{{r + {R_N}}} = \dfrac{E}{{r + \left( {{R_d} + {R_x}} \right)}}\) Để đèn sáng bình thường thì: \(I = {I_{dm}} \Rightarrow {R_x}\) Lời giải chi tiết: Điện trở của bóng đèn: \({R_d} = \dfrac{{U_d^2}}{{{P_d}}} = \dfrac{{{6^2}}}{6} = 6\Omega \) Cường độ định mức qua đèn là: \({I_{dm}} = \dfrac{{{P_d}}}{{{I_d}}} = \dfrac{6}{6} = 1A\) Cường độ dòng điện chạy trong mạch: \(I = \dfrac{E}{{r + {R_N}}} = \dfrac{E}{{r + \left( {{R_d} + {R_x}} \right)}} = \dfrac{{12}}{{4 + 6 + {R_x}}} = \dfrac{{12}}{{10 + {R_x}}}\) Để đèn sáng bình thường thì: \(I = {I_{dm}} \Leftrightarrow \dfrac{{12}}{{10 + {R_x}}} = 1 \Rightarrow {R_x} = 2\Omega \) Chọn D. Câu hỏi 25 : Một nguồn điện một chiều có suất điện động \(12V\) và điện trở trong \(2\Omega \) được nối với điện trở \(R = 10\Omega \) thành mạch điện kín. Bỏ qua điện trở của dây nối. Công suất tỏa nhiệt trên điện trở R là
Đáp án: D Phương pháp giải: + Sử dụng biểu thức định luật ôm cho toàn mạch: \(I = \dfrac{E}{{R + r}}\) + Sử dụng biểu thức tính công suất: \(P = {I^2}R\) Lời giải chi tiết: Ta có: + Cường độ dòng điện qua mạch: \(I = \dfrac{E}{{R + r}} = \dfrac{{12}}{{10 + 2}} = 1A\) + Công suất tỏa nhiệt trên điện trở R: \(P = {I^2}R = {1^2}.10 = 10W\) Chọn D Câu hỏi 26 : Cho mạch điện kín gồm nguồn điện có suất điện động \(E = 12V\), điện trở trong \(r = 2,5\Omega \), mạch ngoài gồm điện trở \({R_1} = 0,5\Omega \) mắc nối tiếp với một biến trở \(R\). Giá trị của R để công suất tiêu thụ trên biến trở \(R\) đạt giá trị cực đại là
Đáp án: D Phương pháp giải: + Sử dụng biểu thức tính điện trở tương đương của đoạn mạch có các điện trở mắc nối tiếp: \(R = {R_1} + {R_2} + ... + {R_n}\) + Sử dụng biểu thức định luật ôm cho toàn mạch: \(I = \dfrac{E}{{R + r}}\) + Sử dụng biểu thức tính công suất tiêu thụ: \(P = {I^2}R\) + Áp dụng bất đẳng thức cosi: \(a + b \ge 2\sqrt {ab} \) Lời giải chi tiết: + Điện trở tương đương mạch ngoài: \({R_N} = {R_1} + R = 0,5 + R\) + Cường độ dòng điện qua mạch: \(I = \dfrac{E}{{{R_N} + r}} = \dfrac{{12}}{{0,5 + R + 2,5}} = \dfrac{{12}}{{R + 3}}\) + Công suất tiêu thụ trên biến trở: \(P = {I^2}R = \dfrac{{{{12}^2}}}{{{{\left( {R + 3} \right)}^2}}}R\) \( \Rightarrow P = \dfrac{{144}}{{{{\left( {\sqrt R + \dfrac{3}{{\sqrt R }}} \right)}^2}}}\) Ta có: \({P_{max}}\) khi \({\left( {\sqrt R + \dfrac{3}{{\sqrt R }}} \right)^2}_{\min }\) Áp dụng bất đẳng thức cosi ta có: \({\left( {\sqrt R + \dfrac{3}{{\sqrt R }}} \right)^2} \ge {\left( {2\sqrt 3 } \right)^2} = 12\) Dấu “=” xảy ra khi \(\sqrt R = \dfrac{3}{{\sqrt R }} \Rightarrow R = 3\Omega \) Chọn D. Câu hỏi 27 : Cho mạch điện như hình vẽ. Biết nguồn điện có suất điện động E = 6V, điện trở trong của nguồn r = 0,1Ω; các điện trở Rđ = 11 Ω; R = 0,9 Ω. a) Viết công thức tính điện trở tương đương của mạch ngoài. Áp dụng số liệu đề bài đã cho để tính điện trở tương đương của mạch ngoài. b) Tính cường độ dòng điện qua mạch.
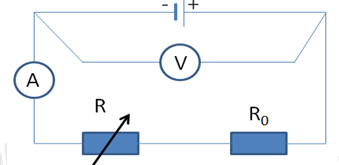
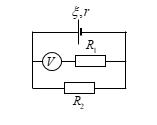
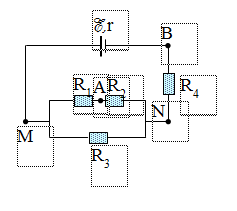
Phương pháp giải: a) Sử dụng biểu thức tính điện trở tương đương của đoạn mạch có các điện trở mắc nối tiếp: \(R = {R_1} + {R_2}\) b) Áp dụng biểu thức định luật Ôm cho toàn mạch: \(I = \dfrac{E}{{R + r}}\) Lời giải chi tiết: a) Ta có mạch ngoài gồm \({R_d}ntR\) \( \Rightarrow \) Điện trở tương đương mạch ngoài: \(R = {R_d} + R = 11 + 0,9 = 11,9\Omega \) b) Cường độ dòng điện qua mạch: \(I = \dfrac{E}{{R + r}} = \dfrac{6}{{11,9 + 0,1}} = 0,5A\) Câu hỏi 28 : Trong giờ thực hành một học sinh mắc một mạch điện như hình vẽ. Biết các dụng vụ đo lý tưởng, R là một biến trở. Suất điện động và điện trở trong lần lượt là \(\xi = 12V,\,\,\,r = 3\Omega \), điện trở \({R_0} = 5\Omega \). 1. Lúc đầu học sinh này điều chỉnh con chạy của biến trở để \(R = 0\). a) Tính cường độ dòng điện trong mạch. b) Tính công suất của nguồn điện. c) Tính nhiệt lượng tỏa ra trên điện trở \({R_0}\) trong thời gian 1 phút. 2. Sau đó học sinh này thay nguồn điện, thay điện trở \({R_0}\) và điều chỉnh biến trở \(R\). Biết rằng: Khi \(R = {R_1}\), vôn kế chỉ 5V, ampe kế chỉ 1A. Khi \(R = {R_2}\), vôn kế chỉ 4V, ampe kế chỉ 2A. Xác định suất điện động và điện trở trong của nguồn điện.
Phương pháp giải: 1. a) Sử dụng biểu thức định luật Ôm cho toàn mạch: \(I = \dfrac{E}{{R + r}}\) b) Sử dụng biểu thức tính công suất: \(P = EI\) c) Sử dụng biểu thức tính nhiệt lượng: \(Q = {I^2}Rt\) 2. Sử dụng biểu thức định luật Ôm Lời giải chi tiết: 1. a. Cường độ dòng điện trong mạch: \(I = \dfrac{E}{{{R_0} + r}} = \dfrac{{12}}{{5 + 3}} = 1,5A\) b. Công suất của nguồn điện: \(P = EI = 12.1,5 = 18W\) c. Nhiệt lượng tỏa ra trên \({R_0}\) trong thời gian \(t = 1' = 60s\) là: \(Q = {I^2}{R_0}t = 1,{5^2}.5.60 = 675J\) 2. Cường độ dòng điện trong mạch: \(I = \dfrac{E}{{R + {R_0} + r}}\) Số chỉ của vôn kế: \({U_V} = E - Ir\) + Khi \(R = {R_1}\): \(\begin{array}{l}\left\{ \begin{array}{l}{I_1} = 1A\\{U_{{V_1}}} = 5V\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}1 = \dfrac{E}{{{R_1} + 5 + r}}\\5 = E - \dfrac{E}{{{R_1} + 5 + r}}r\end{array} \right.\\ \Rightarrow E - r = 5{\rm{ }}\left( 1 \right)\end{array}\)
+ Khi \(R = {R_2}\): \(\begin{array}{l}\left\{ \begin{array}{l}{I_2} = 2A\\{U_{{V_2}}} = 4V\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}2 = \dfrac{E}{{{R_2} + 5 + r}}\\4 = E - \dfrac{E}{{{R_2} + 5 + r}}r\end{array} \right.\\ \Rightarrow E - 2r = 4{\rm{ }}\left( 2 \right)\end{array}\) Từ (1) và (2) ta suy ra: \(\left\{ \begin{array}{l}E = 6V\\r = 1\Omega \end{array} \right.\) Câu hỏi 29 : Người ta mắc hai cực nguồn điện không đổi với một biến trở. Điều chỉnh biến trở, đo hiệu điện thế U giữa hai cực của nguồn và dòng điện I chạy qua mạch ta vẽ lược đồ thị như hình vẽ. Xác định suất điện động và điện trở trong của nguồn.
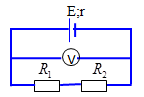
Đáp án: B Phương pháp giải: Điện áp giữa hai cực của nguồn: \(U=\xi -I.r\) Lời giải chi tiết: Điện áp giữa hai cực của nguồn là: \(U=\xi -I.r\) Từ đồ thị ta có: \(U=4,5-I.0,25\) Vậy \(\xi =4,5V;r=0,25\Omega \) Chọn B. Câu hỏi 30 : Một ắc quy có suất điện động 12V và điện trở trong là 2 Ω, , mạch ngoài điện trở R = 6Ω. Khi bị đoản mạch thì cường độ dòng điện qua nguồn là
Đáp án: A Phương pháp giải: Áp dụng công thức :\(I = \frac{E}{{R + r}}\) , khi đoản mạch thì R = 0 Lời giải chi tiết: Ta có : \(I = \frac{E}{{R + r}}\) Khi đoản mạch thì R = 0 → Cường độ dòng điện qua nguồn khi đoản mạch là : \(I = \frac{E}{{R + r}} = \frac{{12}}{2} = 6A\) Chọn A Câu hỏi 31 : Cho mạch điện có sơ đồ như hình vẽ: E = 6V, r = 1Ω, R1 = 0,8Ω, R2 = 2Ω, R3 = 3Ω. Tính hiệu điện thế hai cực của nguồn điện và cường độ dòng điện chạy qua các điện trở.
Phương pháp giải: Áp dụng công thức định luật Ôm cho toàn mạch: \(I = \frac{E}{{r + {R_N}}}\) Hiệu điện thế hai cực của nguồn điện: U = E – I.r Hiệu điện thế hai đầu điện trở: UR = I.R Lời giải chi tiết: Tóm tắt: E = 6V; r = 1Ω; R1 = 0,8Ω; R2 = 2Ω; R3 = 3Ω. Tìm Ung; URi Giải: Sơ đồ mạch ngoài: R1 nt (R2 //R3). Áp dụng công thức định luật Ôm cho toàn mạch: \(I = \frac{E}{{r + {R_N}}} = \frac{6}{{1 + 0,8 + \frac{{2.3}}{{2 + 3}}}} = 2A\) Hiệu điện thế hai cực của nguồn điện: \({U_{ng}} = E--I.r = 6--1.2 = 4V\) Hiệu điện thế hai đầu R1là: \({U_1} = I.{R_1} = 2.0,8 = 1,6{\rm{ }}V\) Hiệu điện thế hai đầu R2 và R3là: \({U_2} = {U_3} = 4--1,6 = 2,4V\) Đáp án: Ung = 4V; U1 = 1,6V ; U2 = U3 = 2,4V. Câu hỏi 32 : Người ta mắc hai cực của nguồn điện với một biến trở có thể thay đổi giá trị từ \(0\) đến vô cùng. Khi giá trị của biến trở rất lớn thì hiệu điện thế giữa hai cực của nguồn điện là \(4,5\,\,V\). Giảm giá trị của biến trở đến khi cường độ dòng điện trong mạch là \(2\,\,A\) thì hiệu điện thế giữa hai cực của nguồn điện là \(4\,\,V\). Suất điện động và điện trở trong của nguồn điện lần lượt là
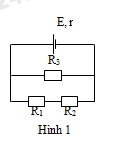
Đáp án: D Phương pháp giải: Định luật Ôm cho toàn mạch: \(I = \frac{E}{{R + r}}\) Hiệu điện thế giữa hai cực nguồn điện: \(U = E - I.r\) Lời giải chi tiết: Khi \(R \to \infty \), cường độ dòng điện trong mạch là: \(I = \frac{E}{{R + r}} = \frac{E}{{\infty + r}} = 0\) Hiệu điện thế giữa hai cực của nguồn điện là: \(U = E - I.r = E - 0 \Rightarrow E = U = 4,5\,\,\left( V \right)\) Khi cường độ dòng điện trong mạch \(I = 2A\), hiệu điện thế giữa hai cực nguồn điện là: \(U = E - I.r \Rightarrow 4 = 4,5 - 2.r \Rightarrow r = 0,25\,\,\left( \Omega \right)\) Câu hỏi 33 : Cho mạch điện như hình bên với E = 18 V; r = 2 Ω; R1 = 15 Ω; R2 =10 Ω và V là vôn kế có điện trở rất lớn. Bỏ qua điện trở dây nối. Số chỉ của vôn kế là
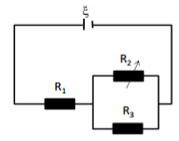
Đáp án: D Phương pháp giải: Phương pháp : Cường độ dòng điện chạy trong mạch : \(I = \frac{E}{{r + {R_N}}}\) Lời giải chi tiết: Cách giải : Cường độ dòng điện chạy trong mạch : \(I = \frac{E}{{r + {R_N}}} = \frac{E}{{r + {R_1} + {R_2}}} = \frac{{18}}{{2 + 15 + 10}} = \frac{2}{3}A\) Số chỉ của vôn kế là : \(U = I.\left( {{R_1} + {R_2}} \right) = \frac{2}{3}.\left( {15 + 10} \right) = 16,7V\) Chọn D Câu hỏi 34 : Cho mạch điện như hình 1. Biết R1 = 1\(\Omega \), R2 = 5\(\Omega \); R3 = 12\(\Omega \); E= 3V, r = 1\(\Omega \). Bỏ qua điện trở của dây nối. Hiệu điện thế giữa hai đầu điện R1 có giá trị:
Đáp án: A Phương pháp giải: Áp dụng định luật Ôm Lời giải chi tiết: Tổng trở của mạch là: \(R=\frac{({{R}_{1}}+{{R}_{2}}).{{R}_{3}}}{{{R}_{1}}+{{R}_{2}}+{{R}_{3}}}=4\Omega \) Dòng điện trong mạch: \(I=\frac{E}{R+r}=0,6A\) Hiệu điện thế giữa hai đầu điện R12 có giá trị: U12 = E – I.r = 2,4 (V) Dòng điện đi qua điện trở R1 là: \({{I}_{1}}=I-{{I}_{3}}=I-\frac{{{U}_{12}}}{{{R}_{3}}}=0,6-\frac{2,4}{12}=0,4(A)\) Hiệu điện thế giữa hai đầu điện R1 có giá trị: U1 = I1. R1 = 0,4 (V) Chọn A Câu hỏi 35 : Cho mạch điện như hình vẽ. Nguồn điện có suất điện động \(E = 9\,\,V\) và điện trở trong \(r = 1\,\,\Omega \). Đèn có ghi \(6V - 3W\). Bỏ qua điện trở của dây nối. Giá trị của biến trở R để đèn sáng bình thường là
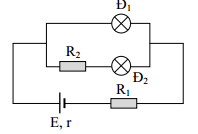
Đáp án: B Phương pháp giải: Định luật Ôm cho toàn mạch : \(I=\frac{E}{r+R}\) Công suất: \(P=UI={{I}^{2}}R=\frac{{{U}^{2}}}{R}\) Đèn sáng bình thường khi các giá trị dòng điện trên đèn bằng các giá trị định mức Lời giải chi tiết: Điện trở và cường độ dòng điện định mức của bóng đèn là: \(\left\{ \begin{array}{l} Đèn sáng bình thường nên dòng điện qua đèn là \(I = 0,5\,\,A\) Áp dụng định luật Ôm cho toàn mạch, ta có: \(I=\frac{E}{r+{{R}_{b}}+{{R}_{d}}}=0,5A\Rightarrow \frac{9}{1+{{R}_{b}}+12}=0,5\Rightarrow {{R}_{b}}=5\Omega \) Chọn B. Câu hỏi 36 : Một ắc quy có suất điện động E, điện trở trong r mắc với mạch ngoài tạo thành mạch kín. Khi dòng điện qua nguồn là I1 = 0,5A thì công suất mạch ngoài là P1 = 5,9W, còn khi dòng điện qua nguồn là I2 = 1A thì công suất mạch ngoài là P2 = 11,6W. Chọn đáp án đúng.
Đáp án: A Phương pháp giải: Áp dụng công thức tính công suất và công thức định luật Ôm cho toàn mạch : \(\left\{ \begin{array}{l} Lời giải chi tiết: ta có \(\left\{ \begin{array}{l} Câu hỏi 37 : Cho mạch điện có sơ đồ như hình bên. Các bóng đèn có ghi Đ1 (60 V – 30 W) và Đ2 (25 V – 12,5 W). Nguồn điện có suất điện động E = 66V, điện trở trong r = 1Ω và các bóng đèn sáng bình thường. Giá trị của R1 là
Đáp án: C Phương pháp giải: Mạch gồm hai điện trở nối tiếp có : R = R1 + R2, I = I1 = I2; U = U1 + U2 Mạch gồm hai điện trở song song có : \(R=\frac{{{R}_{1}}{{R}_{2}}}{{{R}_{1}}+R_{2}^{{}}}\) ; I = I1 + I2; U = U1 = U2 Biểu thức định luật ôm cho toàn mạch: \(I=\frac{E}{R+r}\) Biểu thức định luật Ôm cho đoạn mạch chỉ chứa điện trở: \(I=\frac{U}{R}\) Công suất tiêu thụ: P = UI Bóng đèn sáng bình thường khi dòng điện chạy qua đèn có các giá trị bằng giá trị định mức Lời giải chi tiết: Đèn sáng bình thường nên : UĐ1 = 60V ; IĐ1 = 0,5A ; RĐ1 = 120Ω UĐ2 = 25V ; IĐ2 = 0,5A ; RĐ1 = 50Ω Cường độ dòng điện mạch chính : I = IĐ1 + IĐ2 = 1A Vì R2 nối tiếp đèn 2 nên U2 = UĐ1- UĐ2 = 35V ; I2 = IĐ2 = 0,5A => R2 = 70Ω Áp dụng định luật Ôm cho toàn mạch : \(I=\frac{E}{R+r}\Rightarrow 1=\frac{66}{R+1}\Rightarrow R=65\Omega \) Điện trở tương đương mạch ngoài : \(R={{R}_{1}}+\frac{{{R}_{D1}}({{R}_{D2}}+{{R}_{2}})}{{{R}_{D1}}+{{R}_{D2}}+{{R}_{2}}}={{R}_{1}}+\text{ }\frac{120.(50+70)}{120+50+70}=65\Omega \Rightarrow {{R}_{1}}=5\Omega \) Chọn C Câu hỏi 38 : Cho mạch điện như hình bên với E = 18V, r = 2Ω, R1 = 15Ω, R2 = 10Ω và V là vôn kế có điện trở rất lớn. Số chỉ của vôn kế là
Đáp án: C Phương pháp giải: Với đoạn mạch điện gồm hai điện trở R1 và R2 mắc song song: \(R=\frac{{{R}_{1}}{{R}_{2}}}{{{R}_{1}}+{{R}_{2}}}\) ; I = I1 + I2, U = U1 = U2 Định luật Ôm cho toàn mạch: \(I=\frac{E}{r+R}\) Định luật Ôm cho đoạn mạch chứa điện trở: U = IR Vôn kế lí tưởng mắc nối tiếp với đoạn mạch nào thì dòng điện đi qua đoạn mạch đó có cường độ bằng 0 Lời giải chi tiết: Vì Vôn kế mắc nối tiếp với R1 nên không có dòng điện qua R1 Cường độ dòng điện qua mạch chính: \(I=\frac{E}{r+{{R}_{2}}}=\frac{18}{2+10}=1,5A\) Số chỉ vôn kế: UV = UR2 = IR2 = 1,5.10 = 15V Chọn C Câu hỏi 39 : Cho mạch điên như hình vẽ. Biết E = 7,8 V; r = 0,4Ω; R1 = R2 = R3 = 3Ω; R4 = 6Ω. Bỏ qua điện trở của dây nối. Dòng điện chạy qua nguồn điện có cường độ là
Đáp án: A Phương pháp giải: Áp dụng định luật Ôm cho toàn mạch Lời giải chi tiết: Điện trở tương đương của mạch ngoài được tính theo công thức \({R_{td}} = {{\left( {{R_1} + {R_3}} \right)\left( {{R_2} + {R_4}} \right)} \over {{R_1} + {R_2} + {R_3} + {R_4}}} = {{\left( {3 + 3} \right)\left( {3 + 6} \right)} \over {3 + 3 + 3 + 6}} = 3,6\Omega \) Cường độ dòng điện trong mạch chính là \(I = {E \over {{R_{td}} + r}} = {{7.8} \over {3,6 + 0,4}} = 1,95A\) Câu hỏi 40 : Một nguồn điện có suất điện động ξ = 12V điện trở trong r = 2Ω nối với điện trở R tạo thành mạch kín. Xác định R biết R > 2Ω, công suất mạch ngoài là 16 W:
Đáp án: B Phương pháp giải: Định luật Ôm cho toàn mạch : \(I = \frac{E}{{r + R}}\) Công suất mạch ngoài : \(P = {I^2}.R\) Lời giải chi tiết: Công suất mạch ngoài : \(P = {I^2}.R\) Mà: \(I = \frac{E}{{r + R}}\) \(\begin{array}{l} Vì \(R > 2\Omega \Rightarrow R = 4\Omega \) Chọn B. Câu hỏi 41 : Cho một nguồn điện có suất điện động E, điện trở trong r và hai vôn kế V1, V2. Khi chỉ mắc vôn kế V1 vào nguồn thì nó chỉ giá trị 80 (V). Khi hai vôn kế mắc nối tiếp vào nguồn thì vôn kế V1 chỉ 60 (V), vôn kế V2 chỉ 30 (V). Hỏi khi hai vôn kế mắc song song rồi nối vào nguồn thì chúng cùng chỉ bao nhiêu?
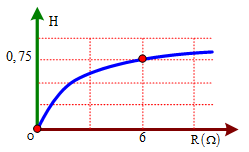
Đáp án: D Phương pháp giải: Điện trở tương đương của đoạn mạch nối tiếp: \({R_{nt}} = {R_1} + {R_2}\) Điện trở tương đương của đoạn mạch song song: \({R_{//}} = \dfrac{{{R_1}{R_2}}}{{{R_1} + {R_2}}}\) Cường độ dòng điện trong mạch: \(I = \dfrac{E}{{r + R}}\) Số chỉ của vôn kế: \({U_V} = I.{R_V}\) Lời giải chi tiết: Gọi điện trở của 2 vôn kế lần lượt là R1 và R2. Khi mắc vôn kế V1 vào nguồn, số chỉ của nó là: \(U = \dfrac{{E{R_1}}}{{r + {R_1}}} = 80\,\,\left( V \right)\,\,\left( 1 \right)\) Khi mắc hai vôn kế nối tiếp vào nguồn, số chỉ của hai vôn kế là: \(\left\{ \begin{array}{l}{U_1} = \dfrac{{E{R_1}}}{{r + {R_1} + {R_2}}} = 60\,\,\left( V \right)\,\,\left( 2 \right)\\{U_2} = \dfrac{{E{R_2}}}{{r + {R_1} + {R_2}}} = 30\,\,\left( V \right)\,\,\left( 3 \right)\end{array} \right.\) Chia phương trình (2) và (3), ta có: \(\dfrac{{{R_1}}}{{{R_2}}} = \dfrac{{60}}{{30}} = 2 \Rightarrow {R_1} = 2{R_2}\) Chia phương trình (1) và (2), ta có: \(\dfrac{{r + {R_1} + {R_2}}}{{r + {R_1}}} = \dfrac{{80}}{{60}} = \dfrac{4}{3} \Rightarrow \dfrac{{r + 2{R_2} + {R_2}}}{{r + 2{R_2}}} = \dfrac{4}{3} \Rightarrow r = {R_2}\) Thay vào phương trình (3), ta có: \(\dfrac{{E{R_2}}}{{{R_2} + 2{R_2} + {R_2}}} = 30 \Rightarrow E = 120\,\,\left( V \right)\) Khi mắc hai vôn kế song song rồi mắc vào nguồn, điện trở tương đương của hai vôn kế là: \({R_{//}} = \dfrac{{{R_1}{R_2}}}{{{R_1} + {R_2}}} = \dfrac{{2{R_2}{R_2}}}{{2{R_2} + {R_2}}} = \dfrac{{2{R_2}}}{3}\) Số chỉ của hai vôn kế khi đó là hiệu điện thế mạch ngoài: \({U_{{V_1}}} = {U_{{V_2}}} = \dfrac{{E.{R_{//}}}}{{r + {R_{//}}}} = \dfrac{{120.\dfrac{{2{R_2}}}{3}}}{{{R_2} + \dfrac{{2{R_2}}}{3}}} = 48\,\,\left( V \right)\) Chọn D. Câu hỏi 42 : Một nguồn điện có suất điện động là \(12\,\,V\) và điện trở trong \(r = 2\,\,\Omega \), mạch ngoài là một biến trở \(R\). Điều chỉnh biến trở \(R\) để công suất tiêu thụ ở mạch ngoài có giá trị cực đại, giá trị cực đại đó là
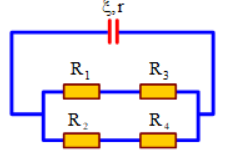
Đáp án: D Phương pháp giải: Công suất tiêu thụ ở mạch ngoài: \(P = {I^2}.R = \frac{{{E^2}}}{{{{(R + r)}^2}}}.R\) Áp dụng bất đẳng thức Cô - si Lời giải chi tiết: Công suất tiêu thụ ở mạch ngoài là: \(P = {I^2}.R = \frac{{{E^2}}}{{{{(R + r)}^2}}}.R \Leftrightarrow P = \frac{{{E^2}}}{{{{\left( {\sqrt R + \frac{r}{{\sqrt R }}} \right)}^2}}}\) Áp dụng bất đẳng thức Cô - si, ta có: \(\sqrt R + \frac{r}{{\sqrt R }} \ge 2\sqrt r \Rightarrow P \le \frac{{{U^2}}}{{4.r}} = \frac{{{{12}^2}}}{{4.2}} = 18{\rm{W}} \Rightarrow {{\rm{P}}_{\max }} = 18{\rm{W}}\) Chọn D. Câu hỏi 43 : Mắc một biến trở \(R\) vào hai cực của một nguồn điện một chiều có suất điện động \(E\) và điện trở trong \(r\). Đồ thị biểu diễn hiệu suất \(H\) của nguồn điện như hình vẽ. Điện trở trong của nguồn điện có giá trị
Đáp án: D Phương pháp giải: Hiệu suất của nguồn điện: \(H = \frac{{{P_{ich}}}}{{{P_{tp}}}} = \frac{R}{{r + R}}\) Lời giải chi tiết: Hiệu suất của nguồn điện là: \(H = \frac{{{P_{ich}}}}{{{P_{tp}}}} = \frac{R}{{r + R}} \Leftrightarrow 0,75 = \frac{6}{{r + 6}} \Leftrightarrow r = 2\Omega \) Chọn D. Câu hỏi 44 : Cho mạch điện có sơ đồ như hình vẽ: Trong đó: E = 1,2 V, r = 0,1\(\Omega \), R1 = R3 = 2\(\Omega \). R2 = R4 = 4\(\Omega \). Hiệu điện thế giữa hai điểm A, B là:
Đáp án: C Phương pháp giải: Phương pháp: + Áp dụng biểu thức xác định điện trở tương đương của mạch + Áp dụng biểu thức định luật Ôm với toàn mạch Lời giải chi tiết: Hướng dẫn giải: Ta có: + Mạch ngoài gồm: R4 nt (R3// (R1 nt R2)) R12 = R1 + R2 = 2 + 4 = 6W - Điện trở đoạn MN là: \({R_{MN}} = \frac{{{R_3}{R_{12}}}}{{{R_3} + {R_{12}}}}{\rm{ = }}1,5\Omega .\) - Điện trở tương đương của mạch ngoài: R = R4 +RMN = 4 + 1,5 = 5,5W - Dòng điện qua mạch chính: \(I{\rm{ }} = \frac{E}{{R + r}} = \frac{{1,2}}{{5,5 + 0,1}} = \frac{3}{{14}}{\rm{ }}A.\) - Hiệu điện thế giữa M, N : \({U_{MN}} = I.{R_{MN}} = \frac{3}{{14}}.1,5 = \frac{9}{{28}}V\) . - Cường độ dòng điện qua R2: \({I_2} = \frac{{{U_{MN}}}}{{{R_1} + {R_2}}} = \frac{{\frac{9}{{28}}}}{6} = \frac{3}{{56}}A\) - Hiệu điện thế giữa A,N: \({U_{AN}} = {I_2}.{R_2} = \frac{3}{{56}}.4 = \frac{3}{{14}}V\) - Hiệu điện thế giữa N và B: \({U_{NB}} = I.{R_4} = \frac{3}{{14}}.4 = \frac{6}{7}V\) . - Hiệu điện thế giữa A và B : \({U_{AB}} = {\rm{ }}{U_{AN}} + {\rm{ }}{U_{NB}} = \frac{3}{{14}} + \frac{6}{7} = 1,07V\) => Chọn C Câu hỏi 45 : Cho mạch điện như hình vẽ. Nguồn điện có điện trở trong bằng \(2\,\,\Omega ;{R_1} = 8\,\,\Omega ;{R_3} = 15\,\,\Omega \). Tính \({R_2}\) để công suất tiêu thụ trên \({R_2}\) đạt cực đại.
Đáp án: C Phương pháp giải: Định luật Ôm cho toàn mạch: \(I = \frac{E}{{R + r}}\) Áp dụng bất đẳng thức Cô - si Lời giải chi tiết: Cường độ dòng điện chạy trong mạch chính là: \(I = {E \over {{R_N} + r}} = {E \over {10 + {{15{R_2}} \over {15 + {R_2}}}}} = {{\left( {{R_2} + 15} \right)E} \over {25{R_2} + 150}}\) Cường độ dòng điện chạy qua \({R_2}\) là: \({I_2} = I.{{{R_{23}}} \over {{R_2}}} = {{E\left( {{R_2} + 15} \right)} \over {25{R_2} + 150}}.{{15{R_2}} \over {{R_2} + 15}}.{1 \over {{R_2}}} = {{15E} \over {25{R_2} + 150}}\) Công suất tiêu thụ trên \({R_2}\) là: \(P = I_2^2{R_2} = {\left( {{{15E} \over {25{R_2} + 150}}} \right)^2}.{R_2} = {{225{E^2}} \over {{{\left( {25\sqrt {{R_2}} + {{150} \over {\sqrt {{R_2}} }}} \right)}^2}}}\) Để \({P_{\max }}\) thì \(25\sqrt {{R_2}} + {{150} \over {\sqrt {{R_2}} }}\) phải nhỏ nhất Theo bất đẳng thức Cô - si ta có: \(25\sqrt {{R_2}} + {{150} \over {\sqrt {{R_2}} }} \ge 2\sqrt {25\sqrt {{R_2}} .{{150} \over {\sqrt {{R_2}} }}} = 50\sqrt 6 \) Dấu “=” xảy ra khi \(25\sqrt {{R_2}} = {{150} \over {\sqrt {{R_2}} }} \Leftrightarrow {R_2} = {{150} \over {25}} = 6\Omega \) Chọn C. Câu hỏi 46 : Cho mạch điện như hình vẽ Suất điện động E = 4V; r = 1Ω. Khi mở khóa K thì cường độ dòng điện thay đổi trị số 2 lần so với khi chưa mở khóa K. Tìm R.
Đáp án: A Phương pháp giải: Áp dụng định luật Ôm cho toàn mach Lời giải chi tiết: Khi mở khóa K, mạch gồm R mắc vào nguồn điện Cường độ dòng điện là \({I_m} = \frac{E}{{R + r}}\) Khi chưa mở khóa K thì mạch được nối tắt R. Cường độ dòng điện là \({I_d} = \frac{E}{r}\) Vì chúng lệch nhau hai lần nên \(\frac{E}{r} = 2.\frac{E}{{r + R}} = > r = R = 1\Omega \) Câu hỏi 47 : Mắc nối tiếp 1 ampe kế với 1 vôn kế vào hai cực của một acquy (điện trở trong của acquy nhỏ không đáng kể), vôn kế chỉ 6V. Người ta mắc thêm một vôn kế như vậy song song với vôn kế ban đầu thì thấy tổng số chỉ của hai vôn kế lúc này là 10V. Nếu mắc song song thêm rất nhiều vôn kế như vậy nữa thì tổng số chỉ của tất cả vôn kế lúc này là
Đáp án: D Phương pháp giải: Lời giải chi tiết: Chọn D Câu hỏi 48 : Mắc nối tiếp 1 ampe kế với 1 vôn kế vào hai cực của một acquy (điện trở trong của acquy nhỏ không đáng kể), vôn kế chỉ 6 V. Người ta mắc thêm một vôn kế như vậy song song với vôn kế ban đầu thì thấy tổng số chỉ của hai vôn kế lúc này là 10 V. Nếu mắc song song thêm rất nhiều vôn kế như vậy nữa thì tổng số chỉ của tất cả các vôn kế lúc này là
Đáp án: C Phương pháp giải: Lời giải chi tiết: Đáp án C - Gọi RA, RV lần lượt là điện trở của mỗi ampe kế và vôn kế, $E$ là suất điện động của acquy. - Khi mắc 1 vôn kế nối tiếp với ampe kế, số chỉ của vôn kế là U1 = 6 V ${U_1} = {E \over {{R_A} + {R_V}}}.{R_V} = 6\,\,V$ (1) - Khi mắc thêm một vôn kế nữa song song với vôn kế ban đầu, mỗi môn kế chỉ U2 = 5 V Ta có: ${U_2} = {E \over {{R_A} + {{{R_V}} \over 2}}}.{{{R_V}} \over 2} = 5\,\,V$ (2) - Từ (1), (2) suy ra: RV = 4RA ;$E = {\rm{ }}7,5{\rm{ }}V$ - Khi có n vôn kế mắc song song thì tổng số chỉ của các vôn kế bằng $${U_0} = \sum {{U_n}} = n{E \over {{R_A} + {{{R_V}} \over n}}}.{{{R_V}} \over n} = {E \over {{1 \over 4} + {1 \over n}}} \approx 4E = 30\,V$$ Câu hỏi 49 : Cho một mạch điện kín gồm nguồn điện có suất điện động E = 12 V, điện trở trong rất nhỏ, mạch ngoài gồm các điện trở R1 = 3 Ω, R2 = 4 Ω, R3 = 5 Ω được mắc nối tiếp. a) Tính cường độ dòng điện chạy trong mạch. b) Tính hiệu điện thế giữa hai đầu điện trở R2. c) Tính công của nguồn điện sản ra trong 10 phút và công suất tỏa nhiệt ở điện trở R3. d) Nếu R3 là biến trở. Xác định R3 để công suất tiêu thụ nhiệt trên R3 đạt cực đại. Lời giải chi tiết: Câu hỏi 50 : Một nguồn điện có suất điện động 6 V, điện trở trong 2 a) Tính R để công suất tiêu thụ của mạch ngoài là 4 W. b) Với giá trị nào của R thì công suất tiêu thụ của mạch ngoài đạt giá trị cực đại. Tính giá trị cực đại đó. Lời giải chi tiết: Quảng cáo
|

















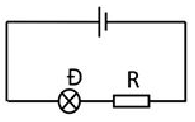



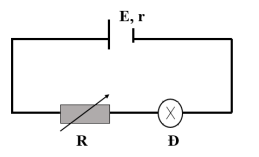
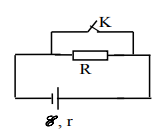


 , mắc với mạch ngoài là một biến trở R để tạo thành một mạch kín.
, mắc với mạch ngoài là một biến trở R để tạo thành một mạch kín.