50 bài tập Đặc trưng vật lí của âm mức độ nhận biết, thông hiểuLàm bàiQuảng cáo
Câu hỏi 1 : Đơn vị đo mức cường độ âm là.
Đáp án: A Phương pháp giải: Lời giải chi tiết: Đáp án A Phương pháp: Sử dụng lí thuyết về sóng âm Đơn vị đo mức cường độ âm làBen (B). Câu hỏi 2 : Giá trị mức cường độ âm mà tài con người có thể nghe được là
Đáp án: A Phương pháp giải: Lời giải chi tiết: Đáp án A Phương pháp: sử dụng lí thuyết về sóng âm Giá trị mức cường độ âm mà tai con người có thể nghe được từ 0dB đến 130dB Câu hỏi 3 : Khi nói về siêu âm, phát biểu nào sau đây sai?
Đáp án: D Phương pháp giải: Lời giải chi tiết: Đáp án D + Siêu âm có tần số lớn hơn hạ âm → bước sóng sẻ nhỏ hơn → D sai. Câu hỏi 4 : Khi nói về sóng âm, phát biểu nào sau đây là sai?
Đáp án: A Phương pháp giải: Lời giải chi tiết: Đáp án A + Sóng âm không truyền được trong chân không → A sai. Câu hỏi 5 : Một âm có bước sóng 1cm lan truyền trong không khí với tốc độ 330 m/s. Âm đó là
Đáp án: D Phương pháp giải: Sử dụng công thức tính tần số sóng âm, lí thuyết về phân loại sóng âm dựa vào tần số
Lời giải chi tiết: Tần số âm là f = v/λ = 330/0,01 = 33000 Hz > 20000 Hz => siêu âm Đáp án D Câu hỏi 6 : Công thức tính mức cường độ âm theo đơn vị dB là
Đáp án: B Phương pháp giải: Lời giải chi tiết: Đáp án B Câu hỏi 7 : Đại lượng nào sau đây không phải là đặc trưng vật lý của âm?
Đáp án: C Phương pháp giải: Sử dụng lí thuyết đại cương về sóng âm Lời giải chi tiết: Độ cao là đặc trưng sinh lí của âm Chọn C
Câu hỏi 8 : Một nguồn phát ra âm trong môi trường không hấp thụ âm Cường độ âm chuẩn là I0 = 10-12 W/m2. Tại điểm A, ta đo được mức cường độ âm là L = 50dB. Cường độ âm tại A có giá trị là
Đáp án: B Phương pháp giải: Phương pháp: Áp dụng công thức tính mức cường độ âm \(L = 10\lg \frac{I}{{{I_0}}}\) Lời giải chi tiết: Đáp án B Cách giải : Mức cường độ âm đo tại điểm A là L = 50dB do đó ta đo được cường độ âm tại A là: \(L = 10\lg \frac{{{I_A}}}{{{I_0}}} = 50 = > \lg \frac{{{I_A}}}{{{I_0}}} = 5 = > \frac{{{I_A}}}{{{I_0}}} = {10^5} = > {I_A} = {10^5}.{I_0} = {10^5}{.10^{ - 12}} = {10^{ - 7}}\,{\text{W}}/{m^2}\) Câu hỏi 9 : Mức cường độ âm là L = 5,5 dB. So với cường độ âm chuẩn I0 thì cường độ âm tại đó bằng
Đáp án: B Phương pháp giải: Phương pháp: Áp dụng công thức tính mức cường độ âm \(L = 10\lg \frac{I}{{{I_0}}}\) Lời giải chi tiết: Đáp án B Mức cường độ âm L = 5,5 dB so với cường độ âm chuẩn thì ta có \(5,5 = 10\lg \frac{I}{{{I_0}}} = > \frac{I}{{{I_0}}} = {10^{0,55}} = > I = {10^{0,55}}.{I_0} = 3,548{I_0}\) Câu hỏi 10 : Một lá thép mỏng, một đầu cố định đầu còn lại được kích thích để dao động điều hòa, trong 1 s lá thép thực hiện được 12 dao động toàn phần. Một người đứng cách lá thép 1 m, người thứ 2 đứng cách lá thép 4 m. Kết luận nào sau đây là đúng
Đáp án: D Phương pháp giải: Lời giải chi tiết: Đáp án D Câu hỏi 11 : Một nguồn âm P (coi là nguồn điện) phát ra âm đẳng hướng. Hai điểm A, B nằm cùng trên một phương truyền sóng âm có mức cường độ âm lần lượt là 40dB và 30dB. Điểm M nằm trong môi trường truyền sóng sao cho ∆AMB vuông cân ở A, coi rằng môi trường hoàn toàn không hấp thụ âm. Xác định mức cường độ âm tại M
Đáp án: B Phương pháp giải: Phương pháp:Sử dụng công thức tính cường độ âm và mức cường độ âm Lời giải chi tiết: Đáp án B Cách giải:
\(\left\{ \matrix{ Có: MA = AB (tam giác AMB vuông cân tại A) Áp dụng định lí Pi – ta – go trong tam giác vuông MAO có: \(O{M^2} = O{A^2} + A{M^2} = O{A^2}\left[ {1 + {{\left( {\sqrt {10} - 1} \right)}^2}} \right]\) Lại có: \({L_A} - {L_M} = 10.\log \frac{{O{M^2}}}{{O{A^2}}} = 10.\log \left[ {1 + {{\left( {\sqrt {10} - 1} \right)}^2}} \right] \Leftrightarrow 40 - {L_M} = 7,54 \Rightarrow {L_M} = 32,46dB\) Câu hỏi 12 : Mức cường độ âm L của một âm có cường độ là I được xác định bởi công thức
Đáp án: C Phương pháp giải: Lời giải chi tiết: Đáp án C Câu hỏi 13 : Hàng ngày chúng ta đi trên đường nghe được âm do các phương tiện giao thông gây ra là
Đáp án: C Phương pháp giải: Lời giải chi tiết: Đáp án C Hàng ngày chúng ta đi trên đường ghe được âm do các phương tiện giao thông gây ra là tạp âm Câu hỏi 14 : Hai âm có cùng mức cường độ âm chênh lệch nhau 20dB thì tỉ số cường độ âm giữa chúng là:
Đáp án: B Phương pháp giải: Phương pháp: Sử dụng công thức tính hiệu mức cường độ âm: Lời giải chi tiết: Đáp án B Cách giải: Ta có hiệu mức cường độ âm: ${L_2} - {L_1} = 10\log \frac{{I{}_2}}{{{I_1}}} = 20 \to \log \frac{{I{}_2}}{{{I_1}}} = 2 \to {I_2} = {10^2}{I_1}$ => Chọn B Câu hỏi 15 : Mức cường độ âm tại một điểm trong môi trường truyền âm là L = 70dB. Cường độ âm tại điểm đó gấp:
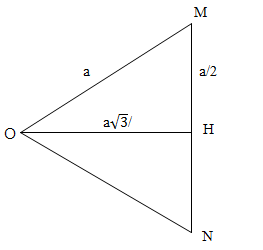
Đáp án: A Phương pháp giải: Phương pháp: Áp dụng công thức tính mức cường độ âm: $L = 10\lg \frac{I}{{{I_0}}}(dB)$ Lời giải chi tiết: Đáp án A Cách giải: Ta có: Mức cường độ âm $L = 10\lg \frac{I}{{{I_0}}}(dB)$ Tại $$L = 70dB = 10\log \frac{I}{{{I_0}}} \to \log \frac{I}{{{I_0}}} = 7 \to I = {10^7}{I_0}$$ => Chọn A Câu hỏi 16 : Một nguồn âm đặt tại O trong môi trường đẳng hướng. Hai điểm M và N trong môi trường tạo với O thành một tam giác đều. Mức cường độ âm tại M và N đều bằng 24,77dB, mức cường độ âm lớn nhất mà một máy thu thu được đặt tại một điểm trên đoạn MN là:
Đáp án: D Phương pháp giải: Phương pháp: Sử dụng công thức tính mức cường độ âm \(L = 10\log \frac{I}{{{I_0}}} = 10\log \frac{P}{{4\pi {r^2}{I_0}}}\) Lời giải chi tiết: Đáp án D Cách giải: + Mức cường độ âm tại 1 điểm cách nguồn một khoảng r là: \(L = 10\log \frac{I}{{{I_0}}} = 10\log \frac{P}{{4\pi {r^2}{I_0}}}\) + Để máy thu đặt tại một điểm trên đoạn MN thu được mức cường độ âm lớn nhất thì khoảng cách từ nguồn O đến điểm đó phải nhỏ nhất => điểm đó là điểm H (H là chân đường cao hạ từ O xuống MN). + Gọi độ dài các cạnh của ∆OMN là a. Áp dụng định lí Pi – ta – go trong tam giác vuông OMH ta có: \(OH = \frac{{a\sqrt 3 }}{2}\) + Mức cường độ âm tại M và H: \(\left\{ \matrix{ Câu hỏi 17 : Đối với sóng âm, khi cường độ âm tăng lên 2 lần thì mức cường độ âm tăng thêm:
Đáp án: D Phương pháp giải: Sử dụng công thức tính mức cường độ âm Lời giải chi tiết: Ta có: \(L = 10\log {I \over {{I_0}}}\) và \(L' = 10\log {{2I} \over {{I_0}}} = 10\log 2 + 10\log {I \over {{I_0}}} = L + 10\log 2(dB)\) Câu hỏi 18 : Trong bài hát “ Tiếng đàn bầu “ của nhạc sỹ Nguyễn Đình Phúc có đoạn: Tiếng đàn bầu của ta cung thanh là tiếng mẹ, cung trầm là giọng cha, ngân nga em vẫn hát, tích tịch tình tang . “ Thanh”và “ trầm” ở đây nói đến đặc trưng nào của âm?
Đáp án: A Phương pháp giải: Lời giải chi tiết: Đáp án A Câu hỏi 19 : Coi cường độ âm chuẩn gần như nha, hỏi tiếng la hét có mức cường độ âm 80 dB có cường độ âm gấp bao nhiêu lần tiếng thì thầm có mức cường độ âm 20 dB?
Đáp án: C Phương pháp giải: Phương pháp : Áp dụng công thức tính mức cường độ âm \(L = 10\log \frac{I}{{{I_0}}}\) Lời giải chi tiết: Đáp án C Cách giải Cường độ âm do tiếng la hét gây ra là \({L_1} = 10\log \frac{{{I_1}}}{{{I_0}}} = 80 = > {I_1} = {I_0}{.10^8}\) Cường độ âm do tiếng thì thầm gây ra là \({L_2} = 10\log \frac{{{I_2}}}{{{I_0}}} = 20 = > {I_2} = {I_0}{.10^2}\) Vậy ta có tỷ số \(\frac{{{I_1}}}{{{I_2}}} = \frac{{{I_0}{{.10}^8}}}{{{I_0}{{.10}^2}}} = {10^6}\) Câu hỏi 20 : Năng lượng của sóng âm truyền trong một đơn vị thời gian, qua một đơn vị diện tích đặt vuông góc với phương truyền được gọi là
Đáp án: C Phương pháp giải: Sử dụng định nghĩa cường độ âm Lời giải chi tiết: Cường độ âm là năng lượng của sóng âm truyền trong một đơn vị thời gian, qua một đơn vị diện tích đặt vuông góc với phương truyền Chọn C Câu hỏi 21 : Một nguồn âm O phát sóng âm theo mọi phương như sau. Khoảng cách từ M đến nguồn bằng 1/10 khoảng cách từ N đến nguồn. Nếu mức cường độ âm tại N là 50 dB thì mức cường độ âm tại M sẽ bằng
Đáp án: C Phương pháp giải: Phương pháp: Mức cường độ âm: $L = 10\log \frac{I}{{{I_0}}} = 10.\log \frac{P}{{4\pi {r^2}{I_0}}}$ (r là khoảng cách từ nguồn đến điểm khảo sát) Lời giải chi tiết: Đáp án C Cách giải: Mức cường độ âm tại M và N: $\eqalign{ Câu hỏi 22 : Một sóng âm truyền trong không khí. Mức cường độ âm tại điểm M và tại điểm N lần lượt là 40 dB và 80 dB. Cường độ âm tại N lớn hơn cường độ âm tại M
Đáp án: D Phương pháp giải: Phương pháp : Áp dụng công thức mức cường độ âm \(L = 10\log \frac{I}{{{I_0}}}\) Lời giải chi tiết: Đáp án D Cách giải: Mức cường độ âm tại M và N lần lượt là \(\eqalign{ Câu hỏi 23 : Lượng năng lượng được sóng âm truyền qua một đơn vị diện tích đặt vuông góc với phương truyền âm trong một đơn vị thời gian gọi là
Đáp án: A Phương pháp giải: Dựa vào định nghĩa cường độ âm Lời giải chi tiết: cường độ âm được xác định bằng mức năng lượng của sóng âm truyên qua một đơn vị diện tích vuông góc với phương truyền sóng. Câu hỏi 24 : Tại một vị trí trong môi trường truyền âm, một sóng âm có cường độ âm I, biết cường độ âm chuẩn là I0. Mức cường độ âm L của sóng âm này tại vị trí đó được tính bằng công thức
Đáp án: D Phương pháp giải: Phương pháp: Công thức tính mức cường độ âm Lời giải chi tiết: Đáp án D Lời giải: Ta có: $L = \log \frac{I}{{{I_0}}}(B) = 10\log \frac{I}{{{I_0}}}(dB)$ => Chọn D Câu hỏi 25 : Tại một điểm, đại lượng đo bằng lượng năng lượng mà sóng âm truyền qua một đơn vị diện tích đặt tại điểm đó, vuông góc với phương truyền sóng trong một đơn vị thời gian là
Đáp án: A Phương pháp giải: định nghĩa cường độ âm Lời giải chi tiết: Tại một điểm, đại lượng đo bằng lượng năng lượng mà sóng âm truyền qua một đơn vị diện tích đặt tại điểm đó, vuông góc với phương truyền sóng trong một đơn vị thời gian là cường độ âm Câu hỏi 26 : Âm có tần số 10Hz là
Đáp án: A Phương pháp giải: Âm có tần số dưới 16Hz là hạ âm Lời giải chi tiết: Âm có tần số dưới 16Hz là hạ âm. Âm có tần số 10Hz là hạ âm. Chọn A Câu hỏi 27 : Biết cường độ âm chuẩn là 10-12 w/m2. Khi cường độ âm tại một điểm là 10-4 W/m2 thì mức cường độ âm tại điểm đó bằng
Đáp án: D Phương pháp giải: Phương pháp : Công thức tính mức cường độ âm: \(L(dB) = 10\log \frac{I}{{{I_0}}} = 80(B).\) Lời giải chi tiết: Cách giải : Mức cường độ âm: \(L(dB) = 10\log \frac{I}{{{I_0}}} = 10.\log \frac{{{{10}^{ - 4}}}}{{{{10}^{ - 12}}}} = 80(B).\) Chọn D Câu hỏi 28 : Con người phân biệt sóng siêu âm, hạ âm, âm thanh dựa vào
Đáp án: C Phương pháp giải: Sóng siêu âm có tần số lớn hơn 20000Hz. Sóng hạ âm có tần số nhỏ hơn 16Hz. Tai người chỉ nghe được âm thanh có tần số nằm trong khoảng từ 16Hz đến 20000Hz. Lời giải chi tiết: Con người phân biệt sóng siêu âm, hạ âm, âm thanh dựa vào khả năng cảm thụ âm của tai người Chọn C Câu hỏi 29 : Trong các đại lượng sau đây của sóng âm, đại lượng nào không đổi khi một sóng âm truyền từ môi trường này sang môi trường khác?
Đáp án: C Phương pháp giải: Đại lượng không đổi khi một sóng âm truyền từ môi trường này sang môi trường khác là tần số của sóng. Lời giải chi tiết: Đại lượng không đổi khi một sóng âm truyền từ môi trường này sang môi trường khác là tần số của sóng. Chọn C Câu hỏi 30 : Sóng cơ truyền trong không khí với cường độ đủ lớn, tai ta có thể cảm thụ được sóng cơ học nào sau đây?
Đáp án: C Phương pháp giải: Tai người nghe được các âm có tần số từ 16 Hz đến 20 000 Hz. Công thức tính chu kì: \(T = \frac{1}{f}\) Lời giải chi tiết: Ta có: \(f = \frac{1}{T} \Rightarrow \left\{ \begin{array}{l} Tai người nghe được các âm có tần số từ 16 Hz đến 20 000 Hz. Vậy tai ta có thể nghe được âm có chu kì 2ms. Chọn C. Câu hỏi 31 : Tại điểm \(M\) trong một môi trường mà sóng âm truyền qua có cường độ âm là \(I\). Biết cường độ âm chuẩn là \({I_0}\). Mức cường độ âm \(L\) tại \(M\) đó được tính bằng công thức
Đáp án: A Phương pháp giải: Lời giải chi tiết: Mức cường độ âm: \(L\left( B \right) = \lg \dfrac{I}{{{I_0}}} \Rightarrow L\left( {dB} \right) = 10\lg \dfrac{I}{{{I_0}}}\) Chọn A. Câu hỏi 32 : Cường độ âm tại một điểm trong môi trường truyền âm là 10-5W/m2. Biết cường độ âm chuẩn là 10-12W/m2. Mức cường độ âm tại điểm đó bằng
Đáp án: D Phương pháp giải: Phương pháp: Áp dụng công thức tính mức cường độ âm: $L = \log \frac{I}{{{I_0}}}(B) = 10\log \frac{I}{{{I_0}}}(dB)$ Lời giải chi tiết: Đáp án D Lời giải: $L = \log \frac{I}{{{I_0}}} = \log \frac{{{{10}^{ - 5}}}}{{{{10}^{ - 12}}}} = 7B = 70dB$ => Chọn D Câu hỏi 33 : Một nguồn phát âm đẳng hướng có mức cường độ âm tại điểm N gần nguồn là 40dB. Biết cường độ âm chuẩn là 10-12 W/m2. Cường độ âm tại N có giá trị
Đáp án: D Phương pháp giải: Sử dụng công thức tính mức cường đô âm Lời giải chi tiết: Ta có \(L = 10\lg {I \over {{I_0}}} \Rightarrow I = {I_0}{10^{{L \over {10}}}} = {10^{ - 12}}{.10^4} = {10^{ - 8}}{\rm{W}}/{m^2}\) Chọn đáp án D Câu hỏi 34 : Các chiến sĩ công an huấn luyện chó nghiệp vụ thường sử dụng chiếc còi như hình ảnh bên. Khi thổi còi này phát ra âm thanh, đó là
Đáp án: A Phương pháp giải: Tai chó nghe được sóng siêu âm Lời giải chi tiết: Tai chó nghe được sóng siêu âm nên còi đó phát ra sóng siêu âm Chọn A Câu hỏi 35 : Một nguồn âm phát âm trong môi trường không hấp thụ âm. Cường độ âm chuẩn là \({I_0} = {10^{ - 12}}\left( {{\rm{W/}}{{\rm{m}}^2}} \right)\). Tại điểm A ta đo được mức cường độ âm là L = 70dB. Cường độ âm I tại A có giá trị là :
Đáp án: D Phương pháp giải: Phương pháp : Công thức tính mức cường độ âm : \(L = 10.\log \frac{I}{{{I_0}}}\,\,\left( {dB} \right)\) Lời giải chi tiết: Cách giải : Ta có : \({L_A} = 10.\log \frac{I}{{{I_0}}} = 70 \Rightarrow \frac{I}{{{I_0}}} = {10^7} \Rightarrow I = {I_0}{.10^7} = {10^{ - 12}}{.10^7} = {10^{ - 5}}\left( {{\rm{W}}/{m^2}} \right)\) Chọn D Câu hỏi 36 : Mức cường độ âm do nguồn S gây ra tại điểm M là L, khi cho S tiến lại gần M một đoạn 62 m thì mức cường độ âm tăng thêm 7 dB. Khoảng cách từ S đến M là:
Đáp án: B Phương pháp giải: Cường độ âm I tại điểm M phụ thuộc vào khoảng cách từ M đến nguồn S theo công thức: \(\text{I = }\frac{\text{P}}{\text{4 }\!\!\pi\!\!\text{ }{{\text{r}}^{\text{2}}}}\) Mức cường độ âm được định nghĩa là: \(\text{L = 10}\text{.lg}\frac{\text{I}}{{{\text{I}}_{\text{0}}}}\text{ (dB)}\) Lời giải chi tiết: Ta có: \({{\text{L}}_{\text{2}}}\text{- }{{\text{L}}_{\text{1}}}\text{ = 10}\text{.lg}\frac{{{\text{I}}_{\text{2}}}}{{{\text{I}}_{\text{1}}}}\text{ = 10}\text{.lg}{{\left( \frac{{{\text{r}}_{\text{1}}}}{{{\text{r}}_{\text{2}}}} \right)}^{\text{2}}}\text{= 20}\text{.lg}\frac{{{\text{r}}_{\text{1}}}}{{{\text{r}}_{\text{2}}}}\) \(\Rightarrow \frac{{{\text{r}}_{\text{1}}}}{{{\text{r}}_{\text{2}}}}\text{ = 2,24}\Rightarrow \frac{{{\text{r}}_{\text{1}}}}{{{\text{r}}_{\text{1}}}-62}=2,24\Rightarrow {{\text{r}}_{\text{1}}}=\text{112 (m)}\) Chọn B Câu hỏi 37 : Chuông gió như hình bên, thường được làm từ những thanh hình ống có chiều dài khác nhau để
Đáp án: B Phương pháp giải: Lời giải chi tiết: Chuông gió được làm từ những thanh hình ống có chiều dài khác nhau là để tạo ra những âm thanh có tần số khác nhau. Chọn B. Câu hỏi 38 : Tại một nhà máy sản xuất, để đảm bảo sức khỏe cho công nhân người ta quy ước mức cường độ âm lớn nhất không quá \(80dB\). Biết cường độ âm chuẩn của âm đó là \({I_0} = {10^{ - 12}}{\rm{W}}/{m^2}\). Cường độ âm lớn nhất nhà máy này có thể phát ra là
Đáp án: B Phương pháp giải: Sử dụng biểu thức tính mức cường độ âm: \(L = 10\log \dfrac{I}{{{I_0}}}\left( {dB} \right)\) Lời giải chi tiết: Mức cường độ âm \(L = 10\log \dfrac{I}{{{I_0}}}\left( {dB} \right)\) \( \Rightarrow \) Cường độ âm lớn nhất nhà máy này có thể phát ra: \(I = {10^{\dfrac{L}{{10}}}}.{I_0} = {10^{\dfrac{{80}}{{10}}}}{.10^{ - 12}} = {10^{ - 4}}{\rm{W}}/{m^2}\) Chọn B Câu hỏi 39 : Khi con ruồi và con muỗi bay, ta nghe được tiếng vo ve từ muỗi bay mà không nghe được từ ruồi là do
Đáp án: A Phương pháp giải: Sử dụng lí thuyết về sóng âm Lời giải chi tiết: Ta có, tai người nghe được âm trong khoảng \(16Hz - 20000Hz\) Ta gnhe được tiếng vo ve từ muỗi bay mà không nghe được từ ruồi là do tần số đập cánh của muỗi thuộc vùng tai người nghe được. Chọn A Câu hỏi 40 : Tại một vị trí trong môi trường truyền âm, khi cường độ âm tăng gấp 10 lần giá trị cường độ âm ban đầu thì mức cường độ âm
Đáp án: C Phương pháp giải: Công thức tính mức cường độ âm \(L = 10\log \frac{I}{{{I_0}}}\) (dB) Lời giải chi tiết: + Mức cường độ âm ban đầu: \(L = 10\log \frac{I}{{{I_0}}}\) (dB) + Sau đó: \(L' = 10\log \frac{{10I}}{{{I_0}}} = 10\log 10 + 10\log \frac{I}{{{I_0}}} = 10 + L\) (dB) Vậy mức cường độ âm tăng 10dB. Chọn C. Câu hỏi 41 : Sóng âm lần lượt truyền trong các môi trường: kim loại, nước và không khí. Tốc độ truyền âm có giá trị
Đáp án: B Phương pháp giải: Vận dụng lí thuyết về sự truyền sóng âm Lời giải chi tiết: Ta có, sóng âm truyền trong các môi trường: \({v_R} > {v_L} > {v_K}\) \( \Rightarrow \) Trong các môi trường đề bài cho, tốc độ truyền âm có giá trị lớn nhất khi truyền trong kim loại và nhỏ nhất khi truyền trong không khí. Chọn B Câu hỏi 42 : Tốc độ truyền âm phụ thuộc vào
Đáp án: A Phương pháp giải: Vận dụng lí thuyết về tốc độ truyền âm Lời giải chi tiết: Tốc độ truyền âm phụ thuộc vào môi trường truyền âm. \({v_R} > {v_L} > {v_K}\) Chọn A Câu hỏi 43 : Một nguồm âm đẳng hướng phát ra từ O. Gọi M và N là hai điểm nằm trên cùng một phương truyền và ở cùng một phía so với O. Mức cường độ âm tại M là 40 dB, tại N là 20 dB. Tính mức cường độ âm tại điểm M khi đặt nguồn âm tại trung điểm I của MN. Coi môi trường không hấp thụ âm.
Đáp án: D Phương pháp giải: Lời giải chi tiết: + Ta có \(\frac{{ON}}{{OM}} = {10^{\frac{{\Delta L}}{{20}}}} = 10 \Rightarrow ON = 10OM\) , chuẩn hóa \(OM = 1 \to ON = 10\) → Trung điểm I của MN cách MN một đoạn 4,5 → Mức cường độ âm tại M khi đi đặt nguồn âm tại I: \({L_{M'}} = {L_M} - 20\log \frac{{IM}}{{OM}} = 40 - 20\log 4,5 = 26,9\)dB. Câu hỏi 44 : Một lá thép mỏng dao động với chu kỳ T = 10-2 s. Hỏi sóng âm do lá thép phát ra là:
Đáp án: D Phương pháp giải: Lời giải chi tiết: Đáp án D Câu hỏi 45 : Sóng cơ học lan truyền trong không khí với cường độ đủ lớn, tai ta có thể cảm thụ được sóng cơ học nào sau đây:
Đáp án: B Phương pháp giải: + Âm nghe được có tần số từ 16 Hz - 20000 Hz + Sử dụng công thức tính tần số âm: \(f = \frac{1}{T}\) Lời giải chi tiết: Âm nghe được có tần số từ 16 Hz - 20000 Hz Tần số âm \(f = \frac{1}{T}\) A: f = 0,5 Hz B: f = 500 Hz C: f = 30 kHz D: f =10 Hz Chọn B Câu hỏi 46 : Khi âm thanh truyền từ không khí vào nước, bước sóng và tần số của âm thanh có thay đổi không?
Đáp án: A Phương pháp giải: Phương pháp: Lý thuyết về sóng âm Lời giải chi tiết: Đáp án A Lời giải: Khi âm truyền từ môi trường này sang môi trường khác thì vận tốc truyền âm thay đổi, bước sóng của sóng âm thay đổi còn tần số của âm thì không thay đổi. => Chọn A Câu hỏi 47 : Đối với âm cơ bản và họa âm bậc 2 của cùng 1 dây đàn phát ra thì
Đáp án: B Phương pháp giải: Phương pháp: Xem lí thuyết mục 5 - họa âm Lời giải chi tiết: Đáp án B Lời giải: Họa âm bậc n có: ${f_n} = {\text{ }}n{f_1}$ Họa âm bậc 2: ${f_2} = {\text{ }}2{f_1}$ => Chọn B Câu hỏi 48 : Một lá thép mỏng, một đầu cố định, đầu còn lại được kích thích để dao động với chu kì không đổi và bằng 0,08 s. Âm do lá thép phát ra là
Đáp án: C Phương pháp giải: Phương pháp: + Sử dụng công thức tính tần số âm: $f = \frac{1}{T}$ + Dựa vào lí thuyết về sóng âm (phần 1) xác định loại âm Lời giải chi tiết: Đáp án C Lời giải: Ta có: $f = \frac{1}{T} = \frac{1}{{0,08}} = 12,5H{\text{z < 16Hz}}$ => Hạ âm => Chọn C Câu hỏi 49 : Biết Io là cường độ âm chuẩn. Tại điểm có cường độ âm I thì mức cường độ âm là
Đáp án: B Phương pháp giải: Lời giải chi tiết: Công thức tính mức cường độ âm: \(L = 10\lg \dfrac{I}{{{I_0}}}\,\,(dB)\) Chọn B Câu hỏi 50 : Tại một điểm M nằm trong môi trường truyền âm có mức cường độ âm là LM = 80 dB. Biết ngưỡng nghe của âm đó là I0 = 10-10 W/m2. Cường độ âm tại M có độ lớn là
Đáp án: B Phương pháp giải: Theo định nghĩa của mức cường độ âm: \(\text{L = 10}\text{.lg}\frac{\text{I}}{{{\text{I}}_{\text{0}}}}\text{ (dB)}\) Lời giải chi tiết: Ta có: \(\text{L = 10}\text{.lg}\frac{\text{I}}{{{\text{I}}_{\text{0}}}}\text{ = 80 dB}\Rightarrow \frac{\text{I}}{{{\text{I}}_{\text{0}}}}={{10}^{8}}\Rightarrow \text{I = 0,01 (W/}{{\text{m}}^{\text{2}}}\text{)}\) Chọn B Quảng cáo
|