50 bài tập Công suất tiêu thụ của mạch điện xoay chiều. Hệ số công suất mức độ nhận biết, thông hiểuLàm bàiQuảng cáo
Câu hỏi 1 : Đặt điện áp xoay chiều vào hai đầu một đoạn mạch mắc nối tiếp gồm điện trở R và cuộn cảm thuần thì cảm kháng của cuộn cảm là ZL. Hệ số công suất của đoạn mạch là
Đáp án: C Phương pháp giải: Lời giải chi tiết: Đáp án C Phương pháp : Công thức tính hệ số công suất của mạch điện xoay chiều Hệ số công suất của đoạn mạch là Câu hỏi 2 : Đặt vào hai đầu đoạn mạch xoay chiều một điện áp u=100cos(100πt+π/2) V thì cường độ dòng điện trong mạch có biểu thức i=100cos(100πt+π/6) mA. Công suất tiêu thụ trong mạch là
Đáp án: A Phương pháp giải: Công suất : P = UI.cosφ Lời giải chi tiết: Công suất tiêu thụ trong mạch : \(P = UI.c{\rm{os}}\varphi = {{100} \over {\sqrt 2 }}.{{{{100.10}^{ - 3}}} \over {\sqrt 2 }}.c{\rm{os}}\left( {{\pi \over 2} - {\pi \over 6}} \right) = 2,5W\) Chọn A Câu hỏi 3 : Hệ số công suất của đoạn mạch RLC nối tiếp không phụ thuộc vào yếu tố nào
Đáp án: B Phương pháp giải: Lời giải chi tiết: Đáp án B Câu hỏi 4 : Công suất tỏa nhiệt của dòng điện xoay chiều được tính theo công thức:
Đáp án: B Phương pháp giải: Lời giải chi tiết: Đáp án B Hướng dẫn giải: Công suất của dòng điện xoay chiều được tính theo công thức: $P = UI\cos \varphi $ Câu hỏi 5 : Trong đoạn mạch RLC nối tiếp, gọi Z là tổng trở của mạch thì hệ số công suất của đoạn mạch được tính bởi:
Đáp án: D Phương pháp giải: Lời giải chi tiết: Đáp án D Hướng dẫn giải: Hệ số công suất của đoạn mạch: $cos\varphi = \frac{R}{Z}$ Câu hỏi 6 : Hệ số công suất của mạch điện xoay chiều gồm RLC mắc nối tiếp dược tính bằng công thức nào?
Đáp án: A Phương pháp giải: Công thức tính hệ số công suất Lời giải chi tiết: Hệ số công suất của mạch RLC là: \(\cos \varphi = \frac{R}{Z}\) Câu hỏi 7 : Công suất của đoạn mạch xoay chiều được tính bằng công thức.
Đáp án: D Phương pháp giải: Công thức tính công suất của đoạn mạch điện xoay chiều Lời giải chi tiết: Công thức tính công suất của đoạn mạch điện xoay chiều là P = U.I.cosφ Câu hỏi 8 : Kết luận nào sau đây là sai khi nói về công suất P của mạch điện xoay chiều có điện áp hiệu dụng U và cường độ hiệu dụng I .
Đáp án: D Phương pháp giải: Công suất của mạch điện luôn là số dương Lời giải chi tiết: Công suất của mạch điện luôn là số dương nên P > 0 Câu hỏi 9 : Đặt điện áp xoay chiều vào hai đầu đoạn mạch có R, L, C mắc nối tiếp. Biết điện trở và tổng trở của đoạn mạch có giá trị lần lượt là 50Ω và \(50\sqrt{2}\Omega \). Hệ số công suất của đoạn mạch là
Đáp án: A Phương pháp giải: Hệ số công suất của đoạn mạch là: \(\cos \varphi =\frac{R}{Z}\) Lời giải chi tiết: Ta có: \(\cos \varphi =\frac{R}{Z}=\frac{50}{50\sqrt{2}}=\frac{1}{\sqrt{2}}=0,71\) Chọn A Câu hỏi 10 : Công suất tỏa nhiệt trung bình của dòng điện xoay chiều được tính theo công thức nào sau đây?
Đáp án: C Phương pháp giải: Lời giải chi tiết: Công suất tỏa nhiệt trung bình của dòng điện xoay chiều là: P = Uicosφ Chọn C. Câu hỏi 11 : Đặt điện áp xoay chiều có tần số góc \(\omega \) vào hai đầu một đoạn mạch nối tiếp gồm điện trở \(R\), tụ điện có điện dung \(C\) và cuộn cảm thuần có độ tự cảm \(L\). Hệ số công suất của đoạn mạch là
Đáp án: B Phương pháp giải: Lời giải chi tiết: Hệ số công suất của đoạn mạch R, L, C nối tiếp là: \(\cos \varphi = \dfrac{R}{{\sqrt {{R^2} + {{\left( {{Z_L} - {Z_C}} \right)}^2}} }} = \dfrac{R}{{\sqrt {{R^2} + {{\left( {L\omega - \dfrac{1}{{C\omega }}} \right)}^2}} }}\) Chọn B. Câu hỏi 12 : Đặt vào hai đầu đoạn mạch chỉ có điện trở thuần 2R điện áp u = U0cosωt V . Công suất tiêu thụ của đoạn mạch là
Đáp án: A Phương pháp giải: Lời giải chi tiết: Đáp án A + Công suất tiêu thụ của đoạn mạch \(P = {{{U^2}} \over {2R}} = {{U_0^2} \over {4R}}.\) Câu hỏi 13 : Mạch điện xoay chiều nào sau đây có hệ số công suất lớn nhất. Với R là điện trở thuần, L là độ tự cảm, C là điện dung:
Đáp án: A Phương pháp giải: Phương pháp: Vận dụng biểu thức tính hệ số công suất của mạch điện xoay chiều:${\text{cos}}\varphi {\text{ = }}\frac{R}{Z}$ Lời giải chi tiết: Đáp án A Hướng dẫn giải: Ta có: ${\text{cos}}\varphi {\text{ = }}\frac{R}{Z}$ =>Mạch chỉ có R hoặc mạch có RLC mắc nối tiếp trong đó ZL = ZC thì cho hệ số công suất lớn nhất bằng 1 Câu hỏi 14 : Công suất của một đoạn mạch RLC nối tiếp có tính dung kháng (ZL < ZC). Nếu ta tăng tần số của dòng điện thì hệ số công suất của mạch:
Đáp án: D Phương pháp giải: Phương pháp: Vận dụng biểu thức tính hệ số công suất Lời giải chi tiết: Đáp án D Hướng dẫn giải: Ta có, hệ số công suất: ${\text{cos}}\varphi {\text{ = }}\frac{R}{Z} = k$ Mạch có tính dung kháng: ZL< ZC Khi ta tăng tần số của dòng điện thì khi đó: + Hiệu số cảm kháng và dung kháng giảm dần về 0, khi đó hệ số công suất tăng dần đến k0 + Sau đó hiệu số cảm kháng và dung kháng tăng dần từ 0 đến giá trị nào đó=> hệ số công suất k giảm từ k0 => Chọn D - k tăng lên rồi giảm Câu hỏi 15 : Một mạch điện RLC nối tiếp có $C = 1/({\omega ^2}L)$. Nếu ta tăng dần giá trị của C thì:
Đáp án: B Phương pháp giải: Phương pháp: Vận dụng biểu thức tính công suất Lời giải chi tiết: Đáp án B Hướng dẫn giải: Theo đầu bài, ta có: + $C = 1/({\omega ^2}L) \leftrightarrow {Z_L} = {Z_C}$khi đó công suất trong mạch đạt giá trị cực đại: ${P_{{\text{max}}}} = \frac{{{U^2}}}{R}$ + Khi tăng dần giá trị của C => tổng trở của mạch tăng => công suất của mạch giảm Câu hỏi 16 : Đoạn mạch RLC nối tiếp có hệ số công suất lớn nhất. Hệ thức nào sau đây không đúng.
Đáp án: D Phương pháp giải: Phương pháp: Vận dụng các biểu thức khi mạch RLC mắc nối tiếp có hệ số công suất lớn nhất Lời giải chi tiết: Đáp án D Hướng dẫn giải: Ta có, mạch RLC mắc nối tiếp có hệ số công suất lớn nhất khi: ${Z_L} = {Z_C}$ Khi đó, ta có: + $\omega = \frac{1}{{\sqrt {LC} }} \to T = \frac{{2\pi }}{\omega } = 2\pi \sqrt {LC} $ + Công suất cực đại: ${P_{{\text{max}}}} = UI$ + Tổng trở khi đó: $Z = R$ + $U = {U_R}$ => Phương án D - sai Câu hỏi 17 : Một mạch điện xoay chiều RLC nối tiếp. Điện áp ở hai đầu đoạn mạch $u = {U_0}\cos \omega t$, cho biết $LC{\omega ^2} = 1$. Nếu ta tăng tần số góc $\omega $ của u thì
Đáp án: B Phương pháp giải: Phương pháp: Vận dụng các biểu thức về điện xoay chiều Lời giải chi tiết: Đáp án B Hướng dẫn giải: Theo đầu bài, ta có: $LC{\omega ^2} = 1 \to {Z_L} = {Z_C}$ => Công suất của mạch cực đại Nếu ta tăng tần số góc $\omega $thì: + Công suất tiêu thụ của mạch giảm + Cường độ hiệu dụng qua mạch giảm: $I = \frac{U}{Z}$ + Tổng trở của đoạn mạch tăng + Hệ số công suất của mạch giảm Ta suy ra: A, C, D - sai B- đúng Câu hỏi 18 : Đặt vào hai đầu đoạn mạch AB một điện áp xoay chiều \({u_{AB}} = 120\sqrt 2 \cos (100\pi t - \frac{\pi }{4})V\) thì cường độ dòng điện qua mạch là \(i = 3\sqrt 2 \cos (100\pi t + \frac{\pi }{{12}})A\). Công suất tiêu thụ của đoạn mạch có giá trị
Đáp án: B Phương pháp giải: Lời giải chi tiết: Đáp án B Công suất tiêu thụ của đoạn mạch : \(P = UI.\cos \varphi = 120.3.\cos \left( { - \frac{\pi }{4} - \frac{\pi }{{12}}} \right) = 180W\) Câu hỏi 19 : Mạch điện xoay chiều nào sau đây có hệ số công suất lớn nhất. Với R là điện trở thuần, L là độ tự cảm, C là điện dung:
Đáp án: A Phương pháp giải: Phương pháp: Vận dụng biểu thức tính hệ số công suất của mạch điện xoay chiều:${\text{cos}}\varphi {\text{ = }}\frac{R}{Z}$ Lời giải chi tiết: Đáp án A Hướng dẫn giải: Ta có: ${\text{cos}}\varphi {\text{ = }}\frac{R}{Z}$ => Mạch chỉ có R hoặc mạch có RLC mắc nối tiếp trong đó ZL = ZC thì cho hệ số công suất lớn nhất bằng 1 Câu hỏi 20 : Hệ số công suất của đọan mạch xoay chiều bằng 0 trong trường hợp nào sau đây?
Đáp án: B Phương pháp giải: Hệ số công suất cosφ = R/Z Lời giải chi tiết: Hệ số công suất cosφ = R/Z = 0 Vậy đoạn mạch có điện trở bằng 0. Câu hỏi 21 : Một nhà máy công nghiệp dùng điện năng để chạy các động cơ. Hệ số công suất do nhà nước qui định phải lớn hơn 0,85 nhằm mục đích chính là để
Đáp án: D Phương pháp giải: lý thuyết truyền tải điện Lời giải chi tiết: Một nhà máy công nghiệp dùng điện năng để chạy các động cơ. Hệ số công suất do nhà nước qui định phải lớn hơn 0,85 nhằm mục đích chính là để hao phí điện năng trên đường dây dẫn điện đến nhà máy ít hơn Câu hỏi 22 : Mạch điện xoay chiều nào sau đây có hệ số công suất nhỏ nhất?
Đáp án: D Phương pháp giải: Hệ số công suất \(\cos \varphi =\frac{R}{Z}=\frac{R}{\sqrt{{{R}^{2}}+{{({{Z}_{L}}-{{Z}_{C}})}^{2}}}}\) Lời giải chi tiết: Mạch không có điện trở thuần thì sẽ có hệ số công suất nhỏ nhất = 0 Chọn D Câu hỏi 23 : Đặt điện áp xoay chiều vào hai đầu đoạn mạch gồm điện trở R, cuộn cảm thuần L và tụ điện C mắc nối tiếp. Biết cảm kháng và dung kháng của đoạn mạch lần lượt là ZL và ZC. Hệ số công suất của đoạn mạch được tính bằng
Đáp án: B Phương pháp giải: Áp dụng công thức tính hệ số công suất của đoạn mạch xoay chiều Lời giải chi tiết: Hệ số công suất của đoạn mạch được tính theo công thức \(\cos \varphi = {R \over Z} = {R \over {\sqrt {{R^2} + {{\left( {{Z_L} - {Z_C}} \right)}^2}} }}\) Chọn đáp án B Câu hỏi 24 : Trong đoạn mạch RLC mắc nối tiếp đang xảy ra hiện tượng cộng hưởng điện. Tăng dần tần số của dòng điện và giữ nguyên các thông số khác của mạch, kết luận nào dưới đây là đúng?
Đáp án: D Phương pháp giải: Khi mạch xảy ra cộng hưởng điện thì cảm kháng bằng dung kháng, cường độ dòng điện lớn nhất, công suất cực đại, hệ số công suất cực đại Lời giải chi tiết: Khi mạch đang xảy ra cộng hưởng mà tăng dần tần số thì hệ số công suất của đoạn mạch giảm. Chọn D Câu hỏi 25 : Đoạn mạch điện xoay chiều không phân nhánh gồm cuộn dây có độ tự cảm L, điện trở thuần R và tụ điện C. Khi có dòng điện tần số góc \(\omega =\frac{1}{\sqrt{LC}}\) chạy qua đoạn mạch thì hệ số công suất của đoạn mạch này
Đáp án: A Phương pháp giải: Điều kiện xảy ra cộng hưởng điện: \(\omega =\frac{1}{\sqrt{LC}}\) Khi mạch điện xảy ra cộng hưởng thì R = Z Hệ số công suất cosφ = R/Z Lời giải chi tiết: Mạch điện xảy ra hiên tượng cộng hưởng. Khi đó Z = R Hệ số công suất của mạch : cosφ = R/Z = 1 Chọn A Câu hỏi 26 : Mạch RLC nối tiếp có \(2\pi f\sqrt {LC} = 1\) . Nếu cho R tăng 2 lần thì hệ số công suất của mạch
Đáp án: A Phương pháp giải: Khi xảy ra cộng hưởng thì : \({Z_L} = {Z_C} \Leftrightarrow 2\pi fL = \frac{1}{{2\pi f.C}} \Leftrightarrow 2\pi f\sqrt {LC} = 1\) Hệ số công suất của mạch : \(\cos \varphi = \frac{R}{Z} = \frac{R}{{\sqrt {{R^2} + {{\left( {{Z_L} - {Z_C}} \right)}^2}} }}\) Lời giải chi tiết: Ta có : \(2\pi f\sqrt {LC} = 1 \Rightarrow {Z_L} = {Z_C}\) Hệ số công suất của mạch: \(\cos \varphi = \frac{R}{Z} = \frac{R}{{\sqrt {{R^2} + {{\left( {{Z_L} - {Z_C}} \right)}^2}} }} = \frac{R}{R} = 1\) dù thay đổi giá trị của R lên gấp đôi thì hệ số công suất không đổi và bằng 1. Chọn A.
Câu hỏi 27 : Mạch điện nào sau đây có hệ số công suất lớn nhất?
Đáp án: A Phương pháp giải: Hệ số công suất của mạch điện: \(\cos \varphi = \dfrac{R}{{\sqrt {{R^2} + {{\left( {{Z_L} - {Z_C}} \right)}^2}} }}\) Lời giải chi tiết: Hệ số công suất của mạch điện lớn nhất khi: \({Z_L} = {Z_C}\) hoặc mạch điện chỉ chứa điện trở. Chọn A. Câu hỏi 28 : Một đoạn mạch không phân nhánh có dòng điện sớm pha hơn hiệu điện thế một góc nhỏ hơn \(\dfrac{\pi }{2}\). Phát biểu nào sau đây là đúng?
Đáp án: C Phương pháp giải: Độ lệch pha giữa hiệu điện thế hai đầu đoạn mạch với cường độ dòng điện: \(\tan \varphi = \dfrac{{{Z_L} - {Z_C}}}{R}\) Cường độ dòng điện hiệu dụng: \(I = \dfrac{U}{{\sqrt {{R^2} + {{\left( {{Z_L} - {Z_C}} \right)}^2}} }}\) Lời giải chi tiết: Dòng điện sớm pha hơn hiện điện thế một góc nhỏ hơn \(\dfrac{\pi }{2}\), ta có: \( - \dfrac{\pi }{2} < \varphi < 0 \Rightarrow \tan \varphi < 0 \Rightarrow \dfrac{{{Z_L} - {Z_C}}}{R} < 0 \Rightarrow {Z_L} - {Z_C} < 0 \Rightarrow {Z_L} < {Z_C}\) Khi tăng tần số dòng điện lên một lượng nhỏ \( \to {Z_L} \uparrow ;{Z_C} \downarrow \Rightarrow \left| {{Z_L} - {Z_C}} \right| \uparrow \Rightarrow I \downarrow \) → C đúng. Chọn C. Câu hỏi 29 : Đặt điện áp \(u = 220\sqrt 2 cos\left( {100\pi t} \right)\left( V \right)\) vào hai đầu của đoạn mạch thì cường độ dòng điện trong đoạn mạch là \(i = 2\sqrt 2 cos\left( {100\pi t} \right)\left( A \right)\). Công suất tiêu thụ của đoạn mạch là
Đáp án: B Phương pháp giải: + Đọc phương trình điện áp và cường độ dòng điện + Sử dụng biểu thức tính công suất tiêu thụ: \(P = UIcos\varphi \) Lời giải chi tiết: Ta có \(\left\{ \begin{array}{l}U = 220V\\I = 2A\end{array} \right.\) Độ lệch pha của u so với i: \(\varphi = {0^0}\) Công suất tiêu thụ của đoạn mạch: \(P = UIcos\varphi = 220.2cos{0^0} = 440W\) Chọn B Câu hỏi 30 : Mạch điện xoay chiều gồm R,L,C mắc nối tiếp có C thay đổi được, có điện áp hai đầu mạch \(u = {U_0}\cos \left( {\omega t + \varphi } \right)\) không đổi. Công suất cực đại khi C có giá trị:
Đáp án: B Phương pháp giải: Công suất của mạch đạt cực đại khi có cộng hưởng: ZL = ZC Lời giải chi tiết: Công suất của mạch đạt cực đại khi có cộng hưởng: \({Z_L} = {Z_C} \Rightarrow \omega L = \dfrac{1}{{\omega C}} \Rightarrow C = \dfrac{1}{{L{\omega ^2}}}\) Chọn B. Câu hỏi 31 : Một đoạn mạch mắc vào điện áp xoay chiều u = 100cos100πt (V) thì cường độ qua đoạn mạch là i = 2.cos(100πt + π/3) (A). Công suất tiêu thụ trong đoạn mạch này là
Đáp án: A Phương pháp giải: Phương pháp: P = UIcosφ Lời giải chi tiết: Đáp án A Cách giải: Công suất tiêu thụ của đoạn mạch: \(P = UIcos\varphi = 50\sqrt 2 .\sqrt 2 .c{\text{os}}\left( {\frac{\pi }{3}} \right) = 50W\) Câu hỏi 32 : Đặt điện áp xoay chiều \(u = 200\sqrt 2 \cos 100\pi t(V)\)vào hai đầu điện trở thuần R = 100Ω. Công suất tỏa nhiệt trên R là
Đáp án: B Phương pháp giải: Lời giải chi tiết: Đáp án B Áp dụng công thức tính công suất tỏa nhiệt trên R ta có \(P = \frac{{{U^2}}}{R} = \frac{{{{200}^2}}}{{100}} = 400W\) Câu hỏi 33 : Đặt điện áp \(u = 100\sqrt 2 \cos 100\pi t(V)\) vào hai đầu một điện trở thuần 50Ω. Công suất tiêu thụ của điện trở bằng
Đáp án: B Phương pháp giải: Phương pháp: Áp dụng công thức tính công suất \(P = \frac{{{U^2}}}{R}\) Lời giải chi tiết: Đáp án B Cách giải: Vì mạch chỉ chứa điện trở thuần do đó công suất của mạch được xác định bởi công thức \(P = \frac{{{U^2}}}{R} = \frac{{{{100}^2}}}{{50}} = 200W\) Câu hỏi 34 : Đặt điện áp xoay chiều vào hai đầu đoạn mạch gồm điện trở R và cuộn cảm thuần mắc nối tiếp. Khi đó, cảm kháng của cuộn cảm có giá trị bằng 2R. Hệ số công suất của đoạn mạch là
Đáp án: D Phương pháp giải: Phương pháp: Hệ số công suất cosφ = R/Z Lời giải chi tiết: Đáp án D Cách giải: Hệ số công suất: \(c{\text{os}}\varphi = \frac{R}{{\sqrt {{R^2} + Z_L^2} }} = \frac{R}{{\sqrt {{R^2} + {{\left( {2R} \right)}^2}} }} = \frac{1}{{\sqrt 5 }} = 0,45\) Câu hỏi 35 : Đặt điện áp u = U0cos(ωt + φ) vào hai đầu đoạn mạch gồm điện trở thuận R và cuộn cảm thuần có độ tự cảm L mắc nối tiếp. Hệ số công suất của đoạn mạch là
Đáp án: B Phương pháp giải: Lời giải chi tiết: Đáp án B Câu hỏi 36 : Đặt điện áp xoay chiều có giá trị hiệu dụng 50V vào hai đầu mạch mắc nối tiếp gồm điện trở thuần 10Ω và cuộn cảm thuần. Biết điện áp hiệu dụng ở hai đầu cuộn cảm thuần là 30V. Công suất tiêu thụ của đoạn mạch bằng:
Đáp án: D Phương pháp giải: Phương pháp : Áp dụng công thức tính công suất tiêu thụ của đoạn mạch xoay chiều Lời giải chi tiết: Đáp án D \({U_R} = \sqrt {{U^2} - U_L^2} = 40V = > P = {{U_R^2} \over R} = 160W\) Câu hỏi 37 : Biết i, I, I0 lần lượt là giá trị tức thời, giá trị hiệu dụng, giá trị cực đại của cường độ dòng điện xoay chiều đi qua một điện trở thuần R trong thời gian t (t >> T, T là chu kì dao động của dòng điện xoay chiều). Nhiệt lượng tỏa ra trên điện trở được xác định theo công thức
Đáp án: D Phương pháp giải: Lời giải chi tiết: Đáp án D Nhiệt lượng toả ra trên điện trở \(Q = R{I^2}t = R{\left( {\frac{{{I_0}}}{{\sqrt 2 }}} \right)^2}t = R\frac{{I_0^2}}{2}t\) Câu hỏi 38 : Cho dòng điện xoay chiều có cường độ i = 5cos100πt A đi qua một điện trở 50 Ω. Nhiệt lượng tỏa ra ở điện trở trong thời gian 1 phút là
Đáp án: C Phương pháp giải: Áp dụng công thức tính nhiệt lượng \(Q = {I^2}Rt \) Đáp án C + Từ phương trình dòng điện, ta có I0 = 5A Nhiệt lượng tỏa ra trên điện trở
Lời giải chi tiết: Đáp án C + Từ phương trình dòng điện, ta có I0 = 5A Nhiệt lượng tỏa ra trên điện trở \(Q = {I^2}Rt = {{I_0^2} \over 2}Rt = {{{5^2}} \over 2}.50.60 = 37500\,J\) Câu hỏi 39 : Đặt vào hai đầu đoạn mạch RLC không phân nhánh một điện áp u = U0cos2πft. Biết điện trở thuần R, độ tự cảm L (cuộn dây thuần cảm), điện dung C của tụ điện và U0 không đổi. Thay đổi tần số f của dòng điện thì hệ số công suất bằng 1 khi
Đáp án: C Phương pháp giải: Lời giải chi tiết: Đáp án C + Hệ số công suất của mạch bằng 1 -> mạch xảy ra cộng hưởng \( \to f = {1 \over {2\pi \sqrt {LC} }}\). Câu hỏi 40 : Hai đầu đoạn mạch chỉ chứa điện trở thuần có một hiệu điện thế không đổi. Nếu điện trở của mạch giảm 2 lần thì công suất của đoạn mạch đó
Đáp án: D Phương pháp giải: sử dụng công thức tính công suất Lời giải chi tiết: Ta có công thức tính công suất : \(P = {I^2}.R = \frac{{{U^2}}}{{{R^2}}}.R = \frac{{{U^2}}}{R}\) Vậy P tỉ lệ nghịch với R, khi R giảm 2 lần thì P tăng 2 lần. Câu hỏi 41 : Đặt điện áp xoay chiều \(u = 100\sqrt 2 \cos \left( {100\pi t - {\pi \over 6}} \right)V\) vào hai đầu đoạn mạch gồm hai phần tử RC. Dòng điện trong mạch i = 2cos(ωt + π/6) A. Tìm công suất tiêu thụ của mạch?
Đáp án: A Phương pháp giải: Sử dụng công thức tính công suất tiêu thụ của mạch điện xoay chiều Lời giải chi tiết: Công suất tiêu thụ của đoạn mạch \(P = UI\cos \varphi = 100.\sqrt 2 \cos {\pi \over 3} = 70,7W\) Chọn A Câu hỏi 42 : Đặt vào hai đầu đoạn mạch xoay chiều điện áp u = 180cos(100pt - p/6)(V) thì cường độ dòng điện qua mạch i = 2sin(100pt + p/6) (A). Công suất tiêu thụ trên đoạn mạch bằng
Đáp án: A Phương pháp giải: Lời giải chi tiết: Công suất tiêu thụ của mạch là\(P = UI\cos \varphi = \frac{{180.2}}{{\sqrt 2 .\sqrt 2 }}.cos30 = 90\sqrt 3 W\) Câu hỏi 43 : Đặt vào hai đầu điện trở một điện áp xoay chiều có giá trị hiệu dụng không đổi và tần số f thay đổi được. Nếu tăng f thì công suất tiêu thụ của điện trở
Đáp án: C Phương pháp giải: Lời giải chi tiết: Đáp án C Mạch điện xoay chiều chỉ có điện trở, công suất tiêu thụ không phụ thuộc vào tần số Câu hỏi 44 : Đặt vào hai đầu đoạn mạch có R, L, C mắc nối tiếp một điện áp xoay chiều có tần số 50 Hz. Biết điện trở R = 50 Ω, cuộn cảm thuần có độ tự cảm \(L = \frac{1}{\pi }H\) tụ điện có điện dung \(C = \frac{1}{{5\pi }}mF\) . Hệ số công suất của đoạn mạch này là
Đáp án: C Phương pháp giải: Lời giải chi tiết:
Câu hỏi 45 : Đặt điện áp u = 100cos(ωt + π/6) (V) vào hai đầu đoạn mạch có điện trở thuần, cuộn cảm thuần và tụ điện mắc nối tiếp thì dòng điện qua mạch là i = 2cos(ωt + π/3) (A). Công suất tiêu thụ của đoạn mạch là
Đáp án: D Phương pháp giải: Áp dụng công thức tính công suất tiêu thụ của đoạn mạch xoay chiều Lời giải chi tiết: Ta có \(P = UI\cos \varphi = {{{U_0}{I_0}\cos \varphi } \over 2} = {{100.2.cos{\pi \over 6}} \over 2} = 50\sqrt 3 {\rm{W}}\) Chọn đáp án D Câu hỏi 46 : Đoạn mạch xoay chiều gồm tụ điện có điện dung C, cuộn dây có độ tự cảm L và điện trở thuần R mắc nối tiếp. Khi dòng điện xoay chiều có tần số góc \(\omega = \frac{1}{{\sqrt {LC} }}\) chạy qua đoạn mạch thì hệ số công suất của đoạn mạch này là
Đáp án: C Phương pháp giải: Khi dòng điện xoay chiều có tần số góc \(\omega = \frac{1}{{\sqrt {LC} }}\) chạy qua đoạn mạch thì trong mạch xảy ra hiện tượng cộng hưởng Lời giải chi tiết: Khi dòng điện xoay chiều có tần số góc \(\omega = \frac{1}{{\sqrt {LC} }}\) chạy qua đoạn mạch thì trong mạch xảy ra hiện tượng cộng hưởng. Hệ số công suất bằng 1 Chọn C Câu hỏi 47 : Đặt điện áp \(u = 100.\cos \left( {100\pi t - \frac{\pi }{4}} \right)V\) vào hai đầu đoạn mạch RLC nối tiếp. Khi đó dòng điện trong mạch có biểu thức \(i = 2.\cos \left( {100\pi t + \frac{\pi }{{12}}} \right)A\). Công suất tiêu thụ của đoạn mạch là :
Đáp án: B Phương pháp giải: Phương pháp : Công suất tiêu thụ của đoạn mạch : P = U.I.cosφ Lời giải chi tiết: Cách giải : Công suất tiêu thụ của đoạn mạch là : \(P = UI\cos \varphi = 50\sqrt 2 .\sqrt 2 .\cos \left( { - \frac{\pi }{4} - \frac{\pi }{{12}}} \right) = 50W\) Chọn B Câu hỏi 48 : Một đoạn mạch xoay chiều gồm một điện trở thuần mắc nối tiếp với một tụ điện. Điện áp hiệu dụng đặt vào hai đầu đoạn mạch là 150V; Cường độ dòng điện chạy trong đoạn mạch có giá trị hiệu dụng là 2A. Điện áp hiệu dụng chạy giữa hai bản tụ điệm là 90V. Công suất tiêu thụ của đoạn mạch là :
Đáp án: C Phương pháp giải: Áp dụng công thức tính công suất tiêu thụ của đoạn mạch xoay chiều là: \(P=UI\cos \varphi \) Lời giải chi tiết: Ta có: \(\text{U}_{\text{R}}^{\text{2}}\text{ = }{{\text{U}}^{\text{2}}}\text{ - U}_{\text{C}}^{\text{2}}={{150}^{2}}-{{90}^{2}}\Rightarrow {{\text{U}}_{\text{R}}}\text{= 120 ( }\!\!\Omega\!\!\text{ )}\) \(\Rightarrow \text{cos }\!\!\varphi\!\!\text{ = }\frac{{{\text{U}}_{\text{R}}}}{\text{U}}\text{ = }\frac{\text{120}}{\text{150}}\text{ = 0,8}\) Công suất tiêu thụ của đoạn mạch là: \(\text{P = UIcos }\!\!\varphi\!\!\text{ = 150}\text{.2}\text{.0,8 = 240 (V)}\) Chọn C Câu hỏi 49 : Mạch điện xoay chiều RLC nối tiếp đặt vào điện áp xoay chiều có giá trị hiệu dụng U, cường độ hiệu dụng qua mạch bằng I, độ lệch pha giữa điện áp và dòng điện là φ. Công suất trung bình mà mạch tiêu thụ không được tính bằng công thức nào dưới đây?
Đáp án: D Phương pháp giải: Công suất trung bình của mạch RLC là \(P=UI\cos \varphi ={{I}^{2}}R=\frac{{{U}^{2}}co{{s}^{2}}\varphi }{R}\) Lời giải chi tiết: Công suất trung bình của mạch RLC là \(P=UI\cos \varphi ={{I}^{2}}R=\frac{{{U}^{2}}co{{s}^{2}}\varphi }{R}\) Công thức P = U2/R chỉ đúng khi mạch chỉ chứa R. Chọn D Câu hỏi 50 : Đặt một điện áp xoay chiều \(u = 200\sqrt 2 \cos (100\pi t - \frac{\pi }{6})(V)\) vào hai đầu đoạn mạch RLC mắc nối tiếp thì cường độ dòng điện trong mạch là \(i = 2\sqrt 2 \cos (100\pi t + \frac{\pi }{6})(A)\). Công suất tiêu thụ trong mạch là
Đáp án: D Phương pháp giải: Áp dụng công thức tính công suất tiêu thụ : \(P = U.I.\cos \varphi \) Lời giải chi tiết: Áp dụng công thức tính công suất tiêu thụ ta có : \(P = U.I.\cos \varphi = 200.2.\cos \left( {\frac{{ - \pi }}{6} - \frac{\pi }{6}} \right) = 200W\)
Chọn D Quảng cáo
|














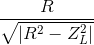
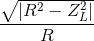
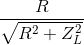
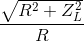
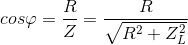
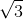 W
W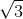 W
W






