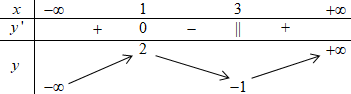40 bài tập trắc nghiệm tương giao đồ thị hàm số mức độ nhận biết, thông hiểuLàm bàiQuảng cáo
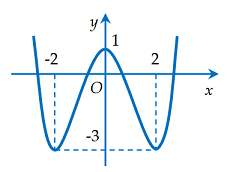
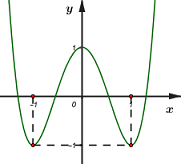
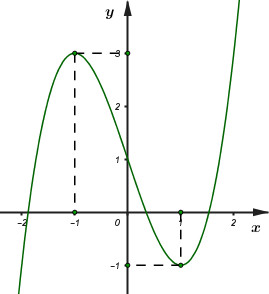
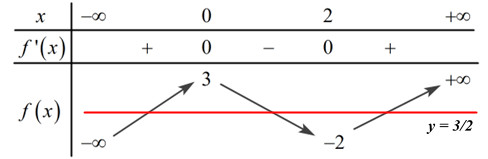
Câu hỏi 1 : Cho hàm số \(f\left( x \right)\) liên tục trên \(\mathbb{R}\) và có đồ thị là đường cong như hình vẽ dưới
Số nghiệm của phương trình \(2f\left( x \right) + 1 = 0\) là:
Đáp án: D Phương pháp giải: Số nghiệm của phương trình \(f\left( x \right) = m\) là số giao điểm của đồ thị hàm số \(y = f\left( x \right)\) và đường thẳng \(y = m\) có tính chất song song với trục hoành. Lời giải chi tiết: Ta có: \(2f\left( x \right) + 1 = 0 \Leftrightarrow f\left( x \right) = \dfrac{{ - 1}}{2}\). Biểu diễn đường thẳng \(y = - \dfrac{1}{2}\) (đường màu đỏ) lên trục tọa độ như sau:
Ta thấy: Đồ thị hàm số \(y = f\left( x \right)\) cắt đồ thị hàm số \(y = - \dfrac{1}{2}\) tại 4 điểm phân biệt \( \Rightarrow \) Phương trình \(2f\left( x \right) + 1 = 0\) có số nghiệm là 4. Chọn D. Câu hỏi 2 : Số giao điểm của đường thẳng \(y = 2\) và đồ thị hàm số \(y = {x^3} + 3{x^2} + 3x - 2\) là
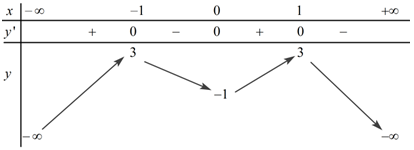
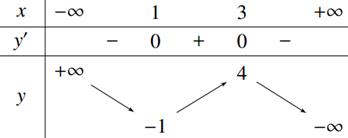
Đáp án: A Phương pháp giải: - Xét phương trình hoành độ giao điểm. - Số nghiệm của phương trình hoành độ giao điểm chính là số giao điểm của 2 đồ thị hàm số. Lời giải chi tiết: Xét phương trình hoành độ giao điểm \({x^3} + 3{x^2} + 3x - 2 = 2\)\( \Leftrightarrow {x^3} + 3{x^2} + 3x - 4 = 0\). Sử dụng MTCT giải phương trình bậc ba, ta thấy phương trình trên có nghiệm duy nhất nên số giao điểm của hai đồ thị hàm số là 1. Chọn A. Câu hỏi 3 : Cho hàm số \(y = f\left( x \right)\) xác định, liên tục trên \(\mathbb{R}\) và có bảng biến thiên như hình bên. Đồ thị hàm số \(y = f\left( x \right)\) cắt đường thẳng \(y = - 2020\) tại bao nhiêu điểm?
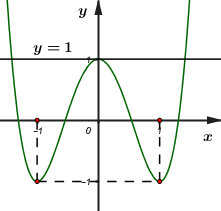
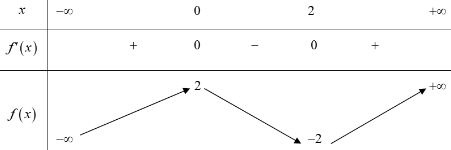
Đáp án: B Phương pháp giải: Dựa vào BBT, nhận xét số giao điểm của đường thẳng \(y = - 2020\) và đồ thị hàm số \(y = f\left( x \right).\) Lời giải chi tiết: Ta có BBT: Dựa vào BBT ta thấy đường thẳng \(y = - 2020\) cắt đồ thị hàm số \(y = f\left( x \right)\) tại \(2\) điểm phân biệt. Chọn B. Câu hỏi 4 : Cho hàm số bậc bốn \(y = f\left( x \right)\) có đồ thị như hình vẽ:
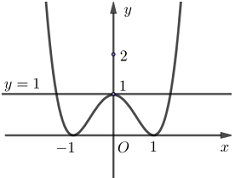
Số nghiệm của phương trình \(f\left( x \right) = 1\) là:
Đáp án: B Phương pháp giải: Số nghiệm của phương trình \(f\left( x \right) = 1\) là số giao điểm của đồ thị hàm số \(y = f\left( x \right)\) và đường thẳng \(y = 1.\) Dựa vào đồ thị hàm số nhận xét số giao điểm của hai đồ thị hàm số và chọn đáp án đúng. Lời giải chi tiết: Số nghiệm của phương trình \(f\left( x \right) = 1\) là số giao điểm của đồ thị hàm số \(y = f\left( x \right)\) và đường thẳng \(y = 1.\) Ta có đồ thị hàm số.
Dựa vào đồ thị hàm số ta thấy đường thẳng \(y = 1\) cắt đồ thị hàm số \(y = f\left( x \right)\) tại 3 điểm phân biệt. \( \Rightarrow \) Phương trình \(f\left( x \right) = 1\) có 3 nghiệm phân biệt. Chọn B. Câu hỏi 5 : Số giao điểm của đồ thị hàm số \(y = 2{x^3} - 3{x^2} + 1\) và trục hoành là:
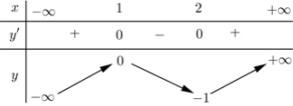
Đáp án: C Phương pháp giải: Số giao điểm của đồ thị hàm số \(y = f\left( x \right)\) và trục hoành là số nghiệm của phương trình \(f\left( x \right) = 0\). Lời giải chi tiết: Xét phương trình hoành độ giao điểm: \(2{x^3} - 3{x^2} + 1 = 0 \Leftrightarrow \left[ \begin{array}{l}x = - \dfrac{1}{2}\\x = 1\end{array} \right.\) Vậy số giao điểm của đồ thị hàm số \(y = 2{x^3} - 3{x^2} + 1\) và trục hoành là 2. Chọn C. Câu hỏi 6 : Cho hàm số \(y = f\left( x \right)\) có bảng biến thiên như sau:
Số nghiệm của phương trình \(f\left( x \right) = 2020\) là:
Đáp án: B Phương pháp giải: - Số nghiệm của phương trình \(f\left( x \right) = m\) là số giao điểm của đồ thị \(y = f\left( x \right)\) và đường thẳng \(y = m\) song song với trục hoành. - Dựa vào BBT xác định số giao điểm. Lời giải chi tiết: Số nghiệm của phương trình \(f\left( x \right) = 2020\) là số giao điểm của đồ thị hàm số \(y = f\left( x \right)\) và đường thẳng \(y = 2020\) song song với trục hoành. Dựa vào đồ thị hàm số ta thấy đường thẳng \(y = 2020\) cắt đồ thị hàm số \(y = f\left( x \right)\) tại 1 điểm duy nhất. Vậy phương trình \(f\left( x \right) = 2020\) có 1 nghiệm duy nhất. Chọn B. Câu hỏi 7 : Số giao điểm của đồ thị hàm số \(y = {x^4} - 2{x^2} + 1\) và đường thẳng \(y = 1\) là:
Đáp án: C Phương pháp giải: Giải phương trình hoành độ giao điểm, số nghiệm của phương trình bằng số giao điểm của đồ thị hàm số. Lời giải chi tiết: Xét phương trình hoành độ giao điểm \({x^4} - 2{x^2} + 1 = 1\) \( \Leftrightarrow {x^4} - 2{x^2} = 0 \Leftrightarrow \left[ \begin{array}{l}x = 0\\x = \sqrt 2 \\x = - \sqrt 2 \end{array} \right.\). Vậy đường thẳng \(y = 1\) cắt đồ thị hàm số \(y = {x^4} - 2{x^2} + 1\) tại 3 điểm phân biệt Chọn C. Câu hỏi 8 : Cho hàm số \(f\left( x \right)\) có bảng biến thiên:
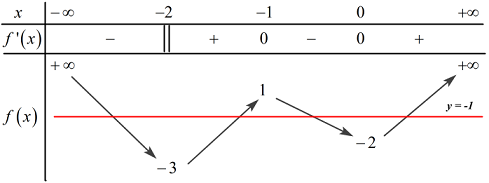
Số nghiệm của phương trình \(f\left( x \right) + 1 = 0\) là:
Đáp án: A Phương pháp giải: Số nghiệm của phương trình \(f\left( x \right) = m\) là số giao điểm của đồ thị hàm số \(y = f\left( x \right)\) và đường thẳng \(y = m\) song song với trục hoành. Lời giải chi tiết: Ta có: \(f\left( x \right) + 1 = 0 \Leftrightarrow f\left( x \right) = - 1\). \( \Rightarrow \) Số nghiệm của phương trình là số giao điểm của đồ thị hàm số \(y = f\left( x \right)\) và đường thẳng \(x = - 1\). Vậy phương trình có 4 nghiệm phân biệt. Chọn A. Câu hỏi 9 : Số giao điểm của đồ thị \(y = {x^3} - 4x + 3\) và đồ thị hàm số \(y = x + 3\) là:
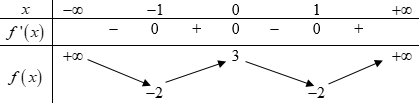
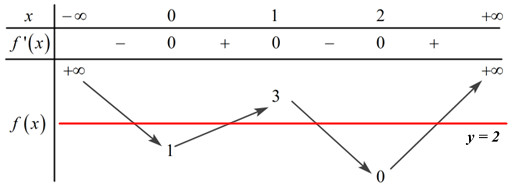
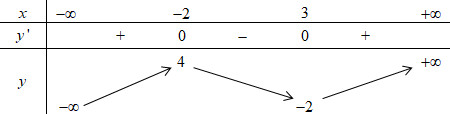
Đáp án: A Phương pháp giải: - Giải phương trình hoành độ giao điểm của hai đồ thị hàm số. - Số nghiệm của phương trình là số giao điểm của đồ thị hai hàm số. Lời giải chi tiết: Hoành độ giao điểm của đồ thị hàm số \(y = {x^3} - 4x + 3\) và đồ thị hàm số \(y = x + 3\) là nghiệm của phương trình: \({x^3} - 4x + 3 = x + 3 \Leftrightarrow {x^3} - 5x = 0 \Leftrightarrow \left[ \begin{array}{l}x = 0\\x = \sqrt 5 \\x = - \sqrt 5 \end{array} \right.\). Vậy đồ thị hai hàm số có 3 giao điểm. Chọn A. Câu hỏi 10 : Hình bên là đồ thị của một hàm số được liệt kê ở bốn phương án A, B, C, D dưới đây. Hàm số đó là
Đáp án: C Phương pháp giải: Dựa vào đồ thị hàm số đã cho, ta thấy hàm số đã cho là hàm bậc ba. Nhận xét các điểm mà đồ thị hàm số đi qua, các điểm cực trị của hàm số rồi suy ra đáp án đúng. Lời giải chi tiết: Dựa vào đồ thị hàm số ta thấy hàm số đã cho làm hàm số bậc ba, có nét cuối đi lên \( \Rightarrow a > 0\) \( \Rightarrow \) loại đáp án A, B. Đồ thị hàm số đã cho có hai điểm cực trị \( \Rightarrow y' = 0\) có hai nghiệm phân biệt. +) Xét đáp án C: \(y = {x^3} - 3x + 1\) \( \Rightarrow y' = 3{x^2} - 3 = 0 \Leftrightarrow \left[ \begin{array}{l}x = 1\\x = - 1\end{array} \right.\) \( \Rightarrow \) Hàm số đã cho có hai điểm cực trị. +) Xét đáp án D: \(y = {x^3} + 3x + 1\) \( \Rightarrow y' = 3{x^2} + 3 > 0\,\,\forall x \in \mathbb{R} \Rightarrow \) hàm số đã cho đồng biến trên \(\mathbb{R}.\) Vậy chỉ có đáp án C đúng. Chọn C. Câu hỏi 11 : Cho hàm số \(y = f\left( x \right)\) xác định, liên tục trên \(\mathbb{R}\) và có bảng biến thiên như sau:
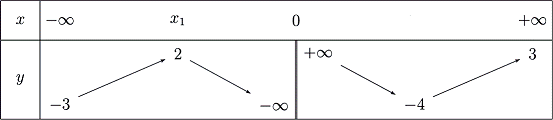
Số nghiệm thực của phương trình \(f\left( x \right) + 1 = 0\) là:
Đáp án: D Phương pháp giải: Số nghiệm của phương trình \(f\left( x \right) = m\) là số giao điểm của đồ thị hàm số \(y = f\left( x \right)\) và đường thẳng \(y = m\). Lời giải chi tiết: Ta có: \(f\left( x \right) + 1 = 0 \Leftrightarrow f\left( x \right) = - 1\). Khi đó số nghiệm của phương trình là số giao điểm của đồ thị hàm số \(y = f\left( x \right)\) và đường thẳng \(y = - 1\). Dựa vào BBT ta thấy đường thẳng \(y = - 1\) cắt đồ thị hàm số tại 2 điểm phân biệt. Vậy phương trình \(f\left( x \right) + 1 = 0\) có 2 nghiệm phân biệt. Chọn D. Câu hỏi 12 : Cho hàm số \(y = f(x)\) liên tục trên đoạn \([ - 1;3]\) và có đồ thị hình bên. Hỏi phương trình \(7f(x) - 5 = 0\) có bao nhiêu nghiệm trên đoạn \([ - 1;3]\) ?
Đáp án: A Phương pháp giải: Số nghiệm của phương trình \(f\left( x \right) = g\left( x \right)\) chính là số giao điểm của hai đồ thị hàm số \(y = f\left( x \right)\) và \(y = g\left( x \right)\) Lời giải chi tiết:
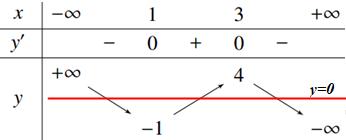
Ta có : \(7f\left( x \right) - 5 = 0 \Leftrightarrow f\left( x \right) = \dfrac{5}{7}\) Đường thẳng \(y = \dfrac{5}{7}\) cắt đồ thị hàm số \(y = f\left( x \right)\) tại 2 điểm phân biệt nên phương trình \(7f\left( x \right) - 5 = 0\) có hai nghiệm phân biệt trên \(\left[ { - 1;3} \right]\) Chọn A. Câu hỏi 13 : Cho hàm số \(y = f\left( x \right)\) liên tục trên \(\mathbb{R}\) và có bảng biến thiên như hình vẽ. Đồ thị hàm số \(y = f\left( x \right)\) và đường thẳng \(y = 0\) có bao nhiêu điểm chung?
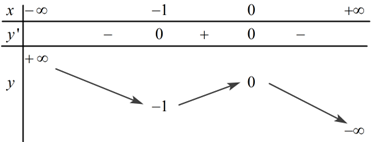
Đáp án: A Phương pháp giải: Vẽ đường thẳng \(y = 0\) và xác định số giao điểm của đường thẳng \(y = 0\) và đồ thị hàm số \(y = f\left( x \right)\). Lời giải chi tiết:
Ta thấy đường thẳng \(y = 0\) cắt đồ thị hàm số \(y = f\left( x \right)\) tại 3 điểm phân biệt nên đồ thị hàm số \(y = f\left( x \right)\) và đường thẳng \(y = 0\) có 3 điểm chung. Chọn A. Câu hỏi 14 : Đồ thị hàm số \(y = {x^3} - 3x - 3\) cắt trục tung tại điểm có tung độ:
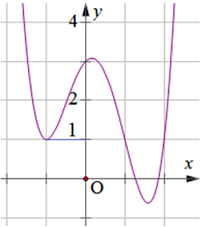
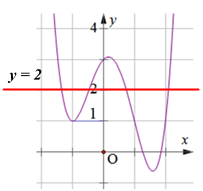
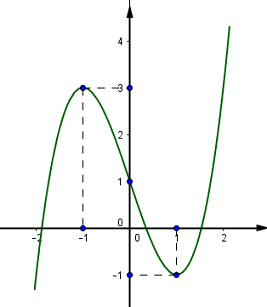
Đáp án: D Phương pháp giải: Đồ thị hàm số cắt trục tung tại điểm có tọa độ \(\left( {0;\,\,{y_0}} \right).\) Lời giải chi tiết: Gọi \(M\left( {0;\,\,{y_0}} \right)\) là điểm mà đồ thị hàm số \(y = {x^3} - 3x - 3\) cắt trục tung. \( \Rightarrow {y_0} = 0 - 3.0 - 3 = - 3 \Rightarrow M\left( {0; - 3} \right).\) Chọn D. Câu hỏi 15 : Tìm số giao điểm của đồ thị hàm số \(y = {x^3} + 2{x^2} - 4x + 1\) và đường thẳng \(y = 2.\)
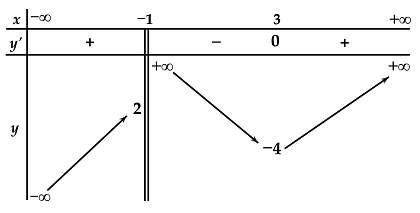
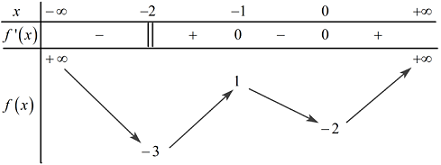
Đáp án: C Phương pháp giải: Số giao điểm của hai đồ thị hàm số \(y = f\left( x \right)\) và \(y = g\left( x \right)\) chính là số nghiệm phân biệt của phương trình hoành độ giao điểm \(f\left( x \right) = g\left( x \right)\). Lời giải chi tiết: Xét phương trình hoành độ giao điểm: \({x^3} + 2{x^2} - 4x + 1 = 2 \Leftrightarrow {x^3} + 2{x^2} - 4x - 1 = 0\) Sử dụng máy tính ta tìm được phương trình trên có 3 nghiệm phân biệt. Vậy hai đồ thị hàm số đã cho cắt nhau tại 3 điểm phân biệt. Chọn C Câu hỏi 16 : Cho hàm số có bảng biến thiên như sau. Tổng các giá trị nguyên của \(m\) để đường thẳng \(y = m\) cắt đồ thị hàm số tại ba điểm phân biệt bằng
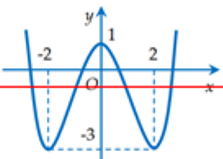
Đáp án: D Phương pháp giải: Số nghiệm của phương trình \(f\left( x \right) = m\) là số giao điểm của đồ thị hàm số \(y = f\left( x \right)\) và đường thẳng \(y = m\) song song với trục hoành. Lời giải chi tiết: Đường thẳng \(y = m\) cắt đồ thị hàm số tại \(3\) điểm phân biệt \( \Leftrightarrow - 4 < m < 2\). Do \(m \in \mathbb{Z}\) nên \(m \in \left\{ { - 3; - 2; - 1;0;1} \right\}\). Vậy tổng các giá trị trên là \(\left( { - 3} \right) + \left( { - 2} \right) + \left( { - 1} \right) + 0 + 1 = - 5\). Chọn D. Câu hỏi 17 : Cho hàm số \(y = f\left( x \right)\) liên tục trên \(\mathbb{R}\) và có bảng biến thiên như hình vẽ bên dưới. Phương trình \(f\left( x \right) - 2 = 0\) có bao nhiêu nghiệm?
Đáp án: D Phương pháp giải: Số nghiệm của phương trình \(f\left( x \right) - 2 = 0\,\, \Leftrightarrow f\left( x \right) = 2\) là số giao điểm của đồ thị hàm số \(y = f\left( x \right)\) và đường thẳng \(y = 2.\) Dựa vào bảng biến thiên rồi tìm số giao điểm của hai đồ thị và chọn đáp án đúng. Lời giải chi tiết: Số nghiệm của phương trình \(f\left( x \right) - 2 = 0\,\, \Leftrightarrow f\left( x \right) = 2\) là số giao điểm của đồ thị hàm số \(y = f\left( x \right)\) và đường thẳng \(y = 2.\) Ta có đồ thị hàm số:
Dựa vào đồ thị hàm số ta thấy đường thẳng \(y = 2\) cắt đồ thị hàm số \[y = f\left( x \right)\] tại 4 điểm phân biệt. \( \Rightarrow \) Phương trình \(f\left( x \right) - 2 = 0\) có 4 nghiệm phân biệt. Chọn D. Câu hỏi 18 : Cho hàm số \(y = f\left( x \right)\) có đồ thị như đường cong trong hình bên dưới.
Số nghiệm của phương trình \(2f\left( x \right) + 3 = 0\) là:
Đáp án: A Phương pháp giải: Số nghiệm của phương trình \(2f\left( x \right) + 3 = 0 \Leftrightarrow f\left( x \right) = - \dfrac{3}{2}\) là số giao điểm của đồ thị hàm số \(y = f\left( x \right)\) và đường thẳng \(y = - \dfrac{3}{2}.\) Dựa vào đồ thị hàm số để biện luận số giao điểm từ đó suy ra số nghiệm của phương trình đã cho. Lời giải chi tiết: Số nghiệm của phương trình \(2f\left( x \right) + 3 = 0 \Leftrightarrow f\left( x \right) = - \dfrac{3}{2}\) là số giao điểm của đồ thị hàm số \(y = f\left( x \right)\) và đường thẳng \(y = - \dfrac{3}{2}.\) Ta có đồ thị hàm số:
Dựa vào đồ thị hàm số ta thấy đường thẳng \(y = - \dfrac{3}{2}\) cắt đồ thị hàm số tại 3 điểm phân biệt. \( \Rightarrow \) Phương trình \(2f\left( x \right) + 3 = 0\) có 3 nghiệm phân biệt. Chọn A. Câu hỏi 19 : Biết đường thẳng \(y = x + 1\) cắt đồ thị hàm số \(y = \dfrac{{2x + 5}}{{x - 1}}\) tại hai điểm phân biệt \(A,\,\,B\) có hoành độ lần lượt là \({x_A},\,{x_B}.\) Khi đó giá trị \({x_A}.{x_B}\) bằng:
Đáp án: A Phương pháp giải: Xét phương trình hoành độ giao điểm \(\left( * \right)\) của hai đồ thị hàm số. Áp dụng hệ thức Vi-et cho phương trình \(\left( * \right)\) rồi chọn đáp án đúng. Lời giải chi tiết: Phương trình hoành độ giao điểm của đường thẳng \(d:\,\,y = x + 1\) và đồ thị hàm số \(\left( C \right):\,\,\,y = \dfrac{{2x + 5}}{{x - 1}}\) là: \(\begin{array}{l}\,\,\,\,\,\,\,x + 1 = \dfrac{{2x + 5}}{{x - 1}}\\ \Leftrightarrow \left( {x + 1} \right)\left( {x - 1} \right) = 2x + 5\\ \Leftrightarrow {x^2} - 1 - 2x - 5 = 0\\ \Leftrightarrow {x^2} - 2x - 6 = 0\,\,\,\,\left( * \right)\end{array}\) Ta có: \(a = 1;\,\,c = - 6 \Rightarrow ac < 0\) \( \Rightarrow \left( * \right)\) luôn có hai nghiệm phân biệt \( \Rightarrow d\) luôn cắt \(\) tại hai điểm phân biệt \(A\left( {{x_A};\,\,{y_A}} \right)\) và \(B\left( {{x_B};\,\,{y_B}} \right)\) với \({x_A},\,\,{x_B}\) là hai nghiệm của phương trình \(\left( * \right)\) Áp dụng hệ thức Vi-et ta có:\({x_A}.{x_B} = \dfrac{c}{a} = - 6.\) Chọn A. Câu hỏi 20 : Cho hàm số \(f\left( x \right) = a{x^4} + b{x^2} + c\,\,\,\left( {a \ne 0} \right)\) có đồ thị như hình vẽ bên dưới:
Số nghiệm của phương trình \(f\left( x \right) - 1 = 0\) là:
Đáp án: A Phương pháp giải: Số nghiệm của phương trìn \(f\left( x \right) - 1 = 0 \Leftrightarrow f\left( x \right) = 1\) là số giao điểm của đồ thị hàm số \(y = f\left( x \right)\) và đường thẳng \(y = 1.\) Dựa vào đồ thị nhận xét số giao điểm và chọn đáp án đúng. Lời giải chi tiết: Số nghiệm của phương trìn \(f\left( x \right) - 1 = 0 \Leftrightarrow f\left( x \right) = 1\) là số giao điểm của đồ thị hàm số \(y = f\left( x \right)\) và đường thẳng \(y = 1.\) Ta có đồ thị hàm số:
Dựa vào đồ thị hàm số ta thấy đường thẳng \(y = 1\) cắt đồ thị hàm số \(y = f\left( x \right)\) tại 3 điểm phân biệt. Vậy phương trình đã cho có 3 nghiệm phân biệt. Chọn A. Câu hỏi 21 : Số giao điểm của đồ thị hàm số \(y = {x^4} - {x^2} - {2^{2020}}\) với trục hoành là:
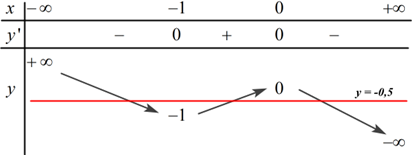
Đáp án: D Phương pháp giải: - Xét phương trình hoành độ giao điểm. - Đặt ẩn phụ \(t = {x^2}\,\,\left( {t \ge 0} \right)\), đưa phương trình về dạng phương trình bậc hai ẩn \(t\). - Tìm số nghiệm của phương trình bậc hai ẩn \(t\), từ đó suy ra số nghiệm \(x\). + 1 nghiệm \(t > 0\) cho 2 nghiệm \(x\). + 1 nghiệm \(t = 0\) cho 1 nghiệm \(x\). + 1 nghiệm \(t < 0\) cho 0 nghiệm \(x\). Lời giải chi tiết: Xét phương trình hoành độ giao điểm \({x^4} - {x^2} - {2^{2020}} = 0\). Đặt \(t = {x^2}\,\,\left( {t \ge 0} \right)\), phương trình trở thành \({t^2} - t - {2^{2020}} = 0\) (*). Ta thấy \(ac = - {2^{2020}} < 0\) nên phương trình (*) có 2 nghiệm phân biệt trái dấu, tức là có 1 nghiệm \(t\) âm và 1 nghiệm \(t\) dương. Vậy phương trình ban đầu có 2 nghiệm phân biệt. Chọn D. Câu hỏi 22 : Cho hàm số bậc ba \(y = f\left( x \right)\) có bảng biến thiên trong hình dưới: Số nghiệm của phương trình \(f\left( x \right) = - 0,5\) là:
Đáp án: B Phương pháp giải: Số nghiệm của phương trình \(f\left( x \right) = - 0,5\) là số giao điểm của đồ thị hàm số \(y = f\left( x \right)\) và đường thẳng \(y = - 0,5.\) Dựa vào BBT để xác định số giao điểm của hai đồ thị hàm số. Lời giải chi tiết: Số nghiệm của phương trình \(f\left( x \right) = - 0,5\) là số giao điểm của đồ thị hàm số \(y = f\left( x \right)\) và đường thẳng \(y = - 0,5.\) Ta có BBT: Dựa vào BBT ta thấy đường thẳng \(y = - 0,5\) cắt đồ thị hàm số \(y = f\left( x \right)\) tại 3 điểm phân biệt. \( \Rightarrow \) Phương trình \(f\left( x \right) = - 0,5\) có \(3\) nghiệm phân biệt. Chọn B. Câu hỏi 23 : Cho hàm số \(y = f\left( x \right)\) liên tục trên \(\mathbb{R}\) và có bảng biến thiên như sau:
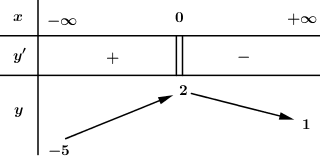
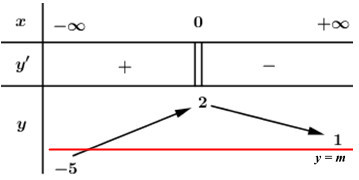
Có bao nhiêu giá trị nguyên của \(m\) để phương trình \(f\left( x \right) = m\) có nghiệm duy nhất?
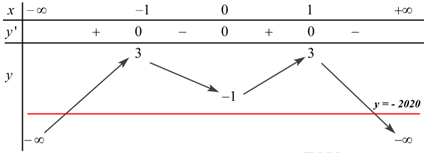
Đáp án: A Phương pháp giải: Phương trình \(f\left( x \right) = m\) là có nghiệm duy nhất \( \Leftrightarrow \) đường thẳng \(y = m\) cắt đồ thị hàm số \(y = f\left( x \right)\) tại 1 điểm duy nhất. Dựa vào BBT để xác định \(m.\) Lời giải chi tiết: Phương trình \(f\left( x \right) = m\) là có nghiệm duy nhất \( \Leftrightarrow \) đường thẳng \(y = m\) cắt đồ thị hàm số \(y = f\left( x \right)\) tại 1 điểm duy nhất.
Dựa vào BBT ta thấy, đường thẳng \(y = m\) cắt đồ thị hàm số \(y = f\left( x \right)\) tại 1 điểm duy nhất \( \Leftrightarrow \left[ \begin{array}{l} - 5 < m \le 1\\m = 2\end{array} \right.\) Lại có: \(m \in \mathbb{Z} \Rightarrow m \in \left\{ { - 4; - 3; - 2; - 1;\,\,0;\,\,1;\,\,2} \right\}\) Vậy có 7 giá trị nguyên của m thỏa mãn bài toán. Chọn A. Câu hỏi 24 : Cho hàm số \(y = f\left( x \right)\) liên tục trên \(\mathbb{R}\) và có đồ thị như hình vẽ bên. Số nghiệm của phương trình \(\left| {f\left( x \right)} \right| = 2\) là:
Đáp án: B Phương pháp giải: Dựa vào đồ thị hàm số để tìm nghiệm. Lời giải chi tiết: Ta có \(\left| {f\left( x \right)} \right| = 2 \Leftrightarrow \left[ \begin{array}{l}f\left( x \right) = 2\\f\left( x \right) = - 2\end{array} \right.\) Với \(f\left( x \right) = 2\) thì đường thẳng \(y = 2\) cắt đồ thị hàm số tại 2 điểm phân biệt. Với \(f\left( x \right) = - 2\) thì đường thẳng \(y = - 2\) cắt đồ thị hàm số tại 2 điẻm phân biệt. Vậy tổng có tất cả 4 nghiệm phân biệt. Chọn B. Câu hỏi 25 : Cho hàm số \(f\left( x \right)\) liên tục trên \(\mathbb{R}\backslash \left\{ 0 \right\}\) và có bảng biến thiên dưới đây.
Số nghiệm của phương trình \(f\left( x \right) = 5\) là
Đáp án: A Phương pháp giải: Dựa vào bảng biến thiên để tìm số giao điểm của đường thẳng \(y = 5\) và đồ thị hàm số. Lời giải chi tiết: Nghiệm của phương trình \(f\left( x \right) = 5\) là số giao điểm của đường thẳng \(y = 5\) và đồ thị hàm số. Dựa vào bảng biến thiên ta thấy đường thẳng \(y = 5 > 3\) cắt đồ thị hàm số tại 1 điểm. Vậy phương trình \(f\left( x \right) = 5\) có duy nhất 1 nghiệm. Chọn A. Câu hỏi 26 : Cho hàm số \(y = f\left( x \right)\) có bảng biến thiên:
Số nghiệm của phương trình \(2f\left( x \right) - 3 = 0\) là:
Đáp án: A Phương pháp giải: Số nghiệm của phương trình \(2f\left( x \right) - 3 = 0 \Leftrightarrow f\left( x \right) = \frac{3}{2}\) là số giao điểm của đồ thị hàm số \(y = f\left( x \right)\) và đường thẳng \(y = \frac{3}{2}\) Dựa vào BBT để biện luận số nghiệm của phương trình. Lời giải chi tiết: Số nghiệm của phương trình \(2f\left( x \right) - 3 = 0 \Leftrightarrow f\left( x \right) = \frac{3}{2}\) là số giao điểm của đồ thị hàm số \(y = f\left( x \right)\) và đường thẳng \(y = \frac{3}{2}\) Ta có BBT:
Dựa vào BBT ta thấy đường thẳng \(y = \frac{3}{2}\) cắt đồ thị hàm số \(y = f\left( x \right)\) tại 3 điểm phân biệt \( \Rightarrow \) Phương trình \(2f\left( x \right) - 3 = 0\) có 3 nghiệm phân biệt. Chọn A. Câu hỏi 27 : Cho hàm số bậc bốn \(y = f\left( x \right)\) có đồ thị như hình bên. Hỏi phương trình \(\left| {f\left( x \right)} \right| = 1\) có bao nhiêu nghiệm?
Đáp án: B Phương pháp giải: - Giải phương trình trị tuyệt đối: \(\left| x \right| = a \Leftrightarrow x = \pm a\). - Sử dụng tương giao đồ thị hàm số: Số nghiệm của phương trình \(f\left( x \right) = m\) là số giao điểm của đồ thị hàm số \(y = f\left( x \right)\) và đường thẳng \(y = m\). Lời giải chi tiết: Ta có: \(\left| {f\left( x \right)} \right| = 1 \Leftrightarrow \left[ \begin{array}{l}f\left( x \right) = 1\,\,\,\,\,\left( 1 \right)\\f\left( x \right) = - 1\,\,\left( 2 \right)\end{array} \right.\). + Số nghiệm của phương trình (1) là số giao điểm của đồ thị hàm số \(y = f\left( x \right)\) và đường thẳng \(y = 1\), suy ra phương trình (1) có 3 nghiệm phân biệt. + Số nghiệm của phương trình (2) là số giao điểm của đồ thị hàm số \(y = f\left( x \right)\) và đường thẳng \(y = - 1\), suy ra phương trình (2) có 4 nghiệm phân biệt. Dễ thấy các nghiệm trên không có nghiệm nào trùng nhau. Vậy phương trình đã cho có 7 nghiệm phân biệt. Chọn B. Câu hỏi 28 : Có bao nhiêu giá trị nguyên của \(m\) để đường thẳng \(y = mx + m + 3\) cắt đồ thị hàm số \(y = {x^3} - 3x + 1\) tại ba điểm phân biệt?
Đáp án: A Phương pháp giải: Số giao điểm của đường thẳng \(d:\,\,\,\,y = mx + m + 3\) và đồ thị hàm số \(\left( C \right):\,\,\,y = {x^3} - 3x + 1\) là số nghiệm của phương trình hoành độ giao điểm (*) của hai đồ thị. \(d\) cắt \(\left( C \right)\) tại ba điểm phân biệt \( \Leftrightarrow \left( * \right)\) có ba nghiệm phân biệt. Lời giải chi tiết: Phương trình hoành độ giao điểm của đường thẳng \(d:\,\,\,\,y = mx + m + 3\) và đồ thị hàm số \(\left( C \right):\,\,\,y = {x^3} - 3x + 1\) là: \({x^3} - 3x + 1 = mx + m + 3\) \( \Leftrightarrow {x^3} - \left( {m + 3} \right)x - m - 2 = 0\,\,\,\,\left( * \right)\) \(\begin{array}{l} \Leftrightarrow {x^3} + {x^2} - {x^2} - x - \left( {m + 2} \right)x - m - 2 = 0\\ \Leftrightarrow {x^2}\left( {x + 1} \right) - x\left( {x + 1} \right) - \left( {m + 2} \right)\left( {x + 1} \right) = 0\\ \Leftrightarrow \left( {x + 1} \right)\left( {{x^2} - x - m - 2} \right) = 0\,\,\,\,\\ \Leftrightarrow \left[ \begin{array}{l}x + 1 = 0\\{x^2} - x - m - 2 = 0\end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l}x = - 1\\g\left( x \right) = {x^2} - x - m - 2 = 0\,\,\,\,\,\left( 1 \right)\end{array} \right.\end{array}\) Số giao điểm của đường thẳng \(d:\,\,\,\,y = mx + m + 3\) và đồ thị hàm số \(\left( C \right):\,\,\,y = {x^3} - 3x + 1\) là số nghiệm của phương trình hoành độ giao điểm (*) của hai đồ thị. \( \Rightarrow \left( * \right)\) có ba nghiệm phân biệt \( \Leftrightarrow \left( 1 \right)\) có hai nghiệm phân biệt \( \ne - 1\) \(\begin{array}{l} \Leftrightarrow \left\{ \begin{array}{l}\Delta > 0\\g\left( { - 1} \right) \ne 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}1 + 4\left( {m + 2} \right) > 0\\{\left( { - 1} \right)^2} - \left( { - 1} \right) - m - 2 \ne 0\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}1 + 4m + 8 > 0\\1 + 1 - m - 2 \ne 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}4m + 9 > 0\\m \ne 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}m > - \dfrac{9}{4}\\m \ne 0\end{array} \right.\end{array}\) \( \Rightarrow \) Có vô số giá trị nguyên của \(m\) thỏa mãn bài toán. Chọn A. Câu hỏi 29 : Cho hàm số \(y = f\left( x \right)\) có bảng biến thiên như sau:
Số nghiệm thực của phương trình \(f\left( x \right) = f\left( 2 \right)\) là:
Đáp án: B Phương pháp giải: Dựa vào bảng biến thiên ta thấy \(f\left( 2 \right) = - 2.\) Số nghiệm của phương trình \(f\left( x \right) = f\left( 2 \right)\) là số giao điểm của đồ thị hàm số \(y = f\left( x \right)\) và đường thẳng \(y = f\left( 2 \right) = - 2.\) Dựa vào BBT rồi biện luận số nghiệm của phương trình. Lời giải chi tiết: Dựa vào bảng biến thiên ta thấy \(f\left( 2 \right) = - 2.\) Số nghiệm của phương trình \(f\left( x \right) = f\left( 2 \right)\) là số giao điểm của đồ thị hàm số \(y = f\left( x \right)\) và đường thẳng \(y = f\left( 2 \right) = - 2.\) Dựa vào BBT ta thấy đường thẳng \(y = - 2\) cắt đồ thị hàm số \(y = f\left( x \right)\) tại 2 điểm phân biệt. Vậy phương trình \(f\left( x \right) = f\left( 2 \right)\) có hai nghiệm phân biệt. Chọn B. Câu hỏi 30 : Cho hàm số \(y = f\left( x \right)\) liên tục trên \(\mathbb{R}\) và có bảng biến thiên như hình bên. Số nghiệm của phương trình \(f\left( x \right) + 1 = 0\) là:
Đáp án: D Phương pháp giải: Số nghiệm của phương trình \(f\left( x \right) + 1 = 0 \Leftrightarrow f\left( x \right) = - 1\) là số giao điểm của đồ thị hàm số \(y = f\left( x \right)\) và đường thẳng \(y = - 1.\) Dựa vào BBT, nhận xét số giao điểm của đồ thị hàm số \(y = f\left( x \right)\) và đường thẳng \(y = - 1.\) Lời giải chi tiết: Số nghiệm của phương trình \(f\left( x \right) + 1 = 0 \Leftrightarrow f\left( x \right) = - 1\) là số giao điểm của đồ thị hàm số \(y = f\left( x \right)\) và đường thẳng \(y = - 1.\)
Dựa vào BBT, ta thấy đường thẳng \(y = - 1\) cắt đồ thị hàm số \(y = f\left( x \right)\) tại 4 điểm phân biệt. Chọn D. Câu hỏi 31 : Đồ thị hàm số \(y = {x^3} - 3{x^2} + 4\) và đường thẳng \(y = - 4x + 8\) có tất cả bao nhiêu điểm chung ?
Đáp án: C Phương pháp giải: - Giải phương trình hoành độ giao điểm. - Số nghiệm của phương trình chính là số điểm chung của hai đồ thị hàm số. Lời giải chi tiết: Hoành độ giao điểm của đồ thị hàm số \(y = {x^3} - 3{x^2} + 4\) và đường thẳng \(y = - 4x + 8\) là nghiệm của phương trình: \(\begin{array}{l}{x^3} - 3{x^2} + 4 = - 4x + 8\\ \Leftrightarrow {x^3} - 3{x^2} + 4x - 4 = 0\\ \Leftrightarrow x = 2\end{array}\) Vậy số giao điểm của hai đồ thị hàm số là 1. Chọn C. Câu hỏi 32 : Cho hàm số \(y = f\left( x \right)\) có đồ thị như đường cong hình dưới.
Phương trình \(f\left( x \right) = 2\) có bao nhiêu nghiệm?
Đáp án: B Phương pháp giải: Số nghiệm của phương trình \(f\left( x \right) = 2\) là số giao điểm của đồ thị hàm số \(y = f\left( x \right)\) và đường thẳng \(y = 2.\) Dựa vào đồ thị hà số để biện luận số nghiệm của phương trình. Lời giải chi tiết: Số nghiệm của phương trình \(f\left( x \right) = 2\) là số giao điểm của đồ thị hàm số \(y = f\left( x \right)\) và đường thẳng \(y = 2.\) Ta có đồ thị hàm số:
Dựa vào đồ thị hàm số ta thấy đường thẳng \(y = 2\) cắt đồ thị hàm số \(y = f\left( x \right)\) tại 4 điểm phân biệt. \( \Rightarrow f\left( x \right) = 2\) có 4 nghiệm phân biệt. Chọn B. Câu hỏi 33 : Cho hàm số \(y = f\left( x \right)\) có đồ thị là đường cong trong hình vẽ bên. Số nghiệm thực của phương trình \(f\left( {x + 2019} \right) = 1\) là:
Đáp án: C Phương pháp giải: Số nghiệm của phương trình \(f\left( x \right) = m\) là số giao điểm của đồ thị hàm số \(y = f\left( x \right)\) và đường thẳng \(y = m\). Lời giải chi tiết:
Dựa vào đồ thị hàm số ta thấy: Đường thẳng \(y = 1\) cắt đồ thị hàm số \(y = f\left( x \right)\) tại 3 điểm phân biệt nên phương trình \(f\left( {x + 2019} \right) = 1\) có 3 nghiệm phân biệt \(\left[ \begin{array}{l}x + 2019 = a\\x + 2019 = b\\x + 2019 = c\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = a - 2019\\x = b - 2019\\x = c - 2019\end{array} \right.\). Chọn C. Câu hỏi 34 : Cho hàm số \(y = f\left( x \right)\) xác định trên \(\mathbb{R}\backslash \left\{ 0 \right\}\), liên tục trên mỗi khoảng xác định và có bảng biến thiên như sau:
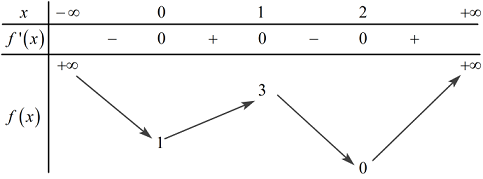
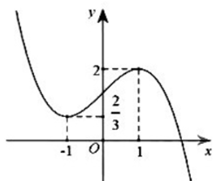
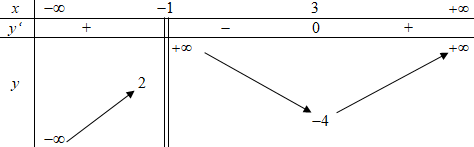
Tìm tất cả các giá trị thực của tham số m để phương trình \(f\left( x \right) = m\) có ba nghiệm thực phân biệt.
Đáp án: A Phương pháp giải: Số nghiệm của phương trình \(f\left( x \right) = m\) là số giao điểm của đồ thị hàm số \(y = f\left( x \right)\) và đường thẳng \(y = m\). Lời giải chi tiết: Số nghiệm của phương trình \(f\left( x \right) = m\) là số giao điểm của đồ thị hàm số \(y = f\left( x \right)\) và đường thẳng \(y = m\). Dựa vào BBT, phương trình \(f\left( x \right) = m\) có 3 nghiệm thực phân biệt khi \(m \in \left( {1;3} \right)\). Chọn A. Câu hỏi 35 : Cho đồ thị hàm số \(y = f\left( x \right)\) như hình vẽ. Tìm số giá trị nguyên của \(m\) để phương trình \(f\left( x \right) = m\) có đúng 3 nghiệm phân biệt.
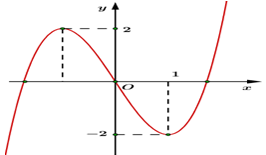
Đáp án: D Phương pháp giải: Số nghiệm của phương trình \(f\left( x \right) = m\) là số giao điểm của đường thẳng \(y = m\) và đồ thị hàm số \(y = f\left( x \right)\). Lời giải chi tiết: Phương trình \(f\left( x \right) = m\) có đúng 3 nghiệm phân biệt khi và chỉ khi đường thẳng \(y = m\) cắt đồ thị hàm số \(y = f\left( x \right)\) tại 3 điểm phân biệt. Từ đồ thị hàm số \(y = f\left( x \right)\) ta thấy đường thẳng \(y = m\) cắt đồ thị hàm số \(y = f\left( x \right)\) tại 3 điểm phân biệt khi và chỉ khi \(\left[ \begin{array}{l}m = 1\\m = 3\end{array} \right..\) Vậy có 2 giá trị nguyên của \(m\) thỏa mãn. Chọn D. Câu hỏi 36 : Cho hàm số bậc bốn trùng phương \(y = f\left( x \right) = a{x^4} + b{x^2} + c\) có đồ thị như hình vẽ:
Số nghiệm thực của phương trình \({f^2}\left( x \right) + 3f\left( x \right) = 0\) là:
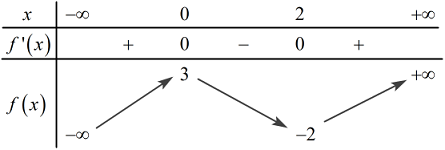
Đáp án: A Phương pháp giải: - Giải phương trình, tìm nghiệm \(f\left( x \right) = m\). - Số nghiệm của phương trình \(f\left( x \right) = m\) là số giao điểm của đồ thị hàm số \(y = f\left( x \right)\) và đường thẳng \(y = m\) có tính chất song song với trục hoành. Lời giải chi tiết: Ta có: \({f^2}\left( x \right) + 3f\left( x \right) = 0 \Leftrightarrow \left[ \begin{array}{l}f\left( x \right) = 0\,\,\,\,\,(1)\\f\left( x \right) = - 3\,\,(2)\end{array} \right.\) Trong đó, phương trình (1) có 2 nghiệm phân biệt, phương trình (2) có 3 nghiệm phân biệt, và các nghiệm của hai phương trình là phân biệt nhau. Vậy phương trình đã cho có tất cả 5 nghiệm. Chọn A. Câu hỏi 37 : Cho hàm số \(y = f\left( x \right)\) có bảng biến thiên như sau:
Số nghiệm của phương trình \(f({x^2} - 2) = 4\) là:
Đáp án: C Phương pháp giải: Số nghiệm của phương trình \(f({x^2} - 2) = 4\) là số giao điểm của phương trình \(y = f\left( {{x^2} - 2} \right)\) và đường thẳng song song với trục hoành. Lời giải chi tiết: Dựa vào BBT ta có: \(f({x^2} - 2) = 4\) \( \Leftrightarrow \left[ \begin{array}{l}{x^2} - 2 = - 2\\{x^2} - 2 = {x_0}\left( {{x_0} > 3} \right)\end{array} \right.\)\( \Leftrightarrow \left[ \begin{array}{l}x = 0\\{x^2} = {x_0} + 2\,\,\,\left( {{x_0} > 3} \right)\end{array} \right.\)\( \Leftrightarrow \left[ \begin{array}{l}x = 0\\x = \pm \sqrt {{x_0} + 2} \,\,\,\left( {{x_0} > 3} \right)\end{array} \right.\) Số nghiệm của phương trình \(f({x^2} - 2) = 4\) là 3. Chọn C. Câu hỏi 38 : Cho hàm số \(y = f\left( x \right)\) có đồ thị như hình vẽ bên. Tìm tất cả các giá trị của tham số m để phương trình \(2f\left( x \right) + 3m - 3 = 0\) có 3 nghiệm thực phân biệt.
Đáp án: A Phương pháp giải: - Xét phương trình hoành độ giao điểm. - Cô lập \(m\). - Dựa vào đồ thị hàm số để xác định \(m\). Lời giải chi tiết: Ta có: \(2f\left( x \right) + 3m - 3 = 0 \Leftrightarrow f\left( x \right) = \dfrac{{3 - 3m}}{2}\) (*) Số nghiệm của phương trình (*) bằng số giao điểm của đồ thị hàm số \(y = f\left( x \right)\) và đường thẳng \(y = \dfrac{{3 - 3m}}{2}\). Để phương trình đã cho có 3 nghiệm phân biệt thì \( - 1 < \dfrac{{3 - 3m}}{2} < 3 \Leftrightarrow - 2 < 3 - 3m < 6\)\( \Leftrightarrow - 5 < - 3m < 3 \Leftrightarrow - 1 < m < \dfrac{5}{3}\). Chọn A. Câu hỏi 39 : Cho hàm số có bảng biến thiên như sau. Tổng các giá trị nguyên của \(m\) để đường thẳng \(y = m\) cắt đồ thị tại ba điểm phân biệt bằng
Đáp án: D Phương pháp giải: Dựa vào bảng biến thiên để xác định giá trị của m. Lời giải chi tiết: Cách giải: Đường thẳng \(y = \ln x\) \(y = m\) cắt đồ thị hàm số tại ba điểm phân biệt khi\( - 4 < m < 2.\) Mà \(m \in \mathbb{Z} \Rightarrow m \in \left\{ { - 3; - 2; - 1;0;1} \right\}.\) Vậy tổng các giá trị nguyên của \(m\) thỏa mãn yêu cầu bài toán bằng \( - 5\). Chọn D. Câu hỏi 40 : Đường thẳng \(y = 4x + 1\) cắt đồ thị hàm số \(y = \dfrac{{x - 2}}{{x + 2}}\) tại bao nhiêu điểm?
Đáp án: B Phương pháp giải: Số giao điểm của 2 đồ thị hàm số \(y = f\left( x \right)\) và \(y = g\left( x \right)\) là số nghiệm của phương trình \(f\left( x \right) = g\left( x \right)\). Lời giải chi tiết: TXĐ : \(D = \mathbb{R}\backslash \left\{ { - 2} \right\}\). Phương trình hoành độ giao điểm của đường thẳng \(y = 4x + 1\) và đồ thị hàm số \(y = \dfrac{{x - 2}}{{x + 2}}\) là: \(\begin{array}{l}4x + 1 = \dfrac{{x - 2}}{{x + 2}}\,\,\,\,\,\,\,\,\left( 1 \right)\\ \Leftrightarrow \left( {4x + 1} \right)\left( {x + 2} \right) = x - 2\\ \Leftrightarrow 4{x^2} + 9x + 2 = x - 2\end{array}\) \(\begin{array}{l} \Leftrightarrow 4{x^2} + 8x + 4 = 0\\ \Leftrightarrow 4{\left( {x + 1} \right)^2} = 0\\ \Leftrightarrow x = - 1\,\,\,\,\left( {tm} \right)\end{array}\) Suy ra phương trình (1) có 1 nghiệm duy nhất hay đường thẳng \(y = 4x + 1\) cắt đồ thị hàm số \(y = \dfrac{{x - 2}}{{x + 2}}\) tại 1 điểm duy nhất. Chọn B. Quảng cáo
|