40 bài tập trắc nghiệm tổng và hiệu của hai vectoLàm bàiQuảng cáo
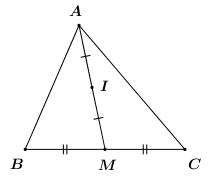
Câu hỏi 1 : Cho tam giác ABC có AM là đường trung tuyến. Gọi I là trung điểm của AM. Trong các mệnh đề sau, mệnh đề nào đúng.
Đáp án: D Phương pháp giải: Sử dụng các đẳng thức vectơ liên quan đến trung điểm: - Nếu I là trung điểm của AB thì \(\overrightarrow {IA} + \overrightarrow {IB} = \overrightarrow 0 \). - Với mọi điểm M, I là trung điểm của AB thì \(\overrightarrow {MA} + \overrightarrow {MB} = 2\overrightarrow {MI} \). Lời giải chi tiết: Vì I là trung điểm của AM nên \(\overrightarrow {IA} + \overrightarrow {IM} = \overrightarrow 0 \). Mà M là trung điểm của BC nên \(\overrightarrow {IB} + \overrightarrow {IC} = 2\overrightarrow {IM} \). Do đó \(\overrightarrow {IB} + \overrightarrow {IC} = 2\overrightarrow {IA} \) hay \(2\overrightarrow {IA} - \overrightarrow {IB} - \overrightarrow {IC} = \overrightarrow 0 \). Đáp án D. Câu 17 (NB): Câu hỏi 2 : Cho tam giác đều ABC có cạnh bằng a. Khi đó \(\left| {\overrightarrow {AB} + \overrightarrow {CA} } \right|\) bằng:
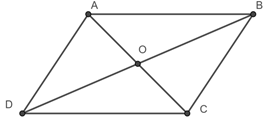
Đáp án: A Phương pháp giải: Sử dụng quy tắc 3 điểm để cộng vectơ. Lời giải chi tiết: Ta có: \(\left| {\overrightarrow {AB} + \overrightarrow {CA} } \right| = \left| {\overrightarrow {CA} + \overrightarrow {AB} } \right|\)\( = \left| {\overrightarrow {CB} } \right| = BC = a\). Đáp án A. Câu hỏi 3 : Cho hình bình hành ABCD có tâm \(O,\,\,G\) là trọng tâm tam giác \(BCD.\) Đẳng thức nào sau đây sai?
Đáp án: A Phương pháp giải: Sử dụng công thức hình bình hành. Lời giải chi tiết: Vì \(ABCD\) là hình bình hành nên ta có:\(\overrightarrow {AB} + \overrightarrow {AD} = \overrightarrow {AC} \Rightarrow \) đáp án A sai. Chọn A. Câu hỏi 4 : Cho ba điểm \(M,\,\,N,\,\,P\) phân biệt. Đẳng thức nào sau đây sai?
Đáp án: D Phương pháp giải: Quy tắc cộng, trừ vectơ cơ bản. Lời giải chi tiết: \(\overrightarrow {NM} + \overrightarrow {PM} = \overrightarrow {NP} \) là đẳng thức sai. Chọn D. Câu hỏi 5 : Tính tổng \(\overrightarrow {MN} + \overrightarrow {PQ} + \overrightarrow {RN} + \overrightarrow {NP} + \overrightarrow {QR} .\)
Đáp án: A Phương pháp giải: Sử dụng quy tắc ba điểm \(\overrightarrow {AB} + \overrightarrow {BC} = \overrightarrow {AC} \). Lời giải chi tiết: Ta có: \(\overrightarrow {MN} + \overrightarrow {PQ} + \overrightarrow {RN} + \overrightarrow {NP} + \overrightarrow {QR} \) \(\begin{array}{l} = \left( {\overrightarrow {MN} + \overrightarrow {NP} } \right) + \left( {\overrightarrow {PQ} + \overrightarrow {QR} } \right) + \overrightarrow {RN} \\ = \overrightarrow {MP} + \overrightarrow {PR} + \overrightarrow {RN} \\ = \overrightarrow {MR} + \overrightarrow {RN} \\ = \overrightarrow {MN} \end{array}\) Chọn A. Câu hỏi 6 : Hình bình hành \(ABCD.\) Tìm vectơ tổng \(\overrightarrow {AB} + \overrightarrow {AC} + \overrightarrow {AD} \)
Đáp án: C Phương pháp giải: Sử dụng qui tắc hình bình hành \(\overrightarrow {AB} + \overrightarrow {AD} = \overrightarrow {AC} \). Lời giải chi tiết: Ta có: \(ABCD\) là hình bình hành nên \(\overrightarrow {AB} + \overrightarrow {AC} + \overrightarrow {AD} \)\( = \left( {\overrightarrow {AB} + \overrightarrow {AD} } \right) + \overrightarrow {AC} \) \( = \overrightarrow {AC} + \overrightarrow {AC} = 2\overrightarrow {AC} \) Chọn C. Câu hỏi 7 : Cho hình bình hành ABCD. Mệnh đề nào sau đây đúng?
Đáp án: A Phương pháp giải: Sử dụng quy tắc hình bình hành. Lời giải chi tiết: Theo quy tắc hình bình hành: \(\overrightarrow {AB} + \overrightarrow {AD} = \overrightarrow {AC} .\) Chọn A. Câu hỏi 8 : Cho hình bình hành ABCD. Tìm \(\overrightarrow u = \overrightarrow {AB} - \overrightarrow {BC} .\)
Đáp án: C Phương pháp giải: Sử dụng quy tắc hình bình hành. Lời giải chi tiết: Ta có: \(\overrightarrow u = \overrightarrow {AB} - \overrightarrow {BC} = \overrightarrow {AB} - \overrightarrow {AD} = \overrightarrow {DB} .\) Chọn C. Câu hỏi 9 : Cho tam giác \(ABC\) đều có cạnh bằng \(3.\) Tính \(\left| {\overrightarrow {AB} + \overrightarrow {AC} } \right|.\)
Đáp án: D Phương pháp giải: Sử dụng công thức trung điểm. Lời giải chi tiết:
Gọi \(M\) là trung điểm của \(BC \Rightarrow AM = \frac{{3\sqrt 3 }}{2}.\) \( \Rightarrow \left| {\overrightarrow {AB} + \overrightarrow {AC} } \right| = \left| {2\overrightarrow {AM} } \right| = 2.3.\frac{{\sqrt 3 }}{2} = 3\sqrt 3 .\) Chọn D. Câu hỏi 10 : Cho hình bình hành \(ABCD\) có tâm \(O.\) Chọn hệ thức đúng trong các hệ thức sau:
Đáp án: A Phương pháp giải: Áp dụng quy tắc hình bình hành. Lời giải chi tiết: Ta có: \(\overrightarrow {AD} + \overrightarrow {AB} = \overrightarrow {AC} = 2\overrightarrow {OC} \) Chọn A. Câu hỏi 11 : Cho 3 điểm \({\rm{A,}}\,{\rm{B,}}\,{\rm{C}}\) thẳng hàng, \(B\) nằm giữa \(A\) và \(C\) sao cho \(AB = 3a,\,\,AC = 4a.\) Khẳng định nào sau đây sai:
Đáp án: B Phương pháp giải: Sử dụng quy tắc cộng vecto. Lời giải chi tiết: Ta có: \(AB = 3a,\,\,AC = 4a,\,\,B\) nằm giữa \(A,\,\,C \Rightarrow BC = AC - AB = 4a - 3a = a.\) Xét đáp án A: \(\left| {\overrightarrow {AB} + \overrightarrow {CB} } \right| = \left| {\overrightarrow {AB} - \overrightarrow {BC} } \right| = \left| {\overrightarrow {AB} - \frac{1}{3}\overrightarrow {AB} } \right| = \frac{2}{3}\left| {\overrightarrow {AB} } \right| = \frac{2}{3}.3a = 2a.\)Ta có: \(AB = 3a,\,\,AC = 4a,\,\,B\) nằm giữa \(A,\,\,C \Rightarrow BC = AC - AB = 4a - 3a = a.\) \( \Rightarrow \) đáp án A đúng. Xét đáp án B: \(\left| {\overrightarrow {BC} + \overrightarrow {BA} } \right| = \left| {\overrightarrow {BC} - 3\overrightarrow {BC} } \right| = 2\left| {\overrightarrow {BC} } \right| = 2a\) \( \Rightarrow \) đáp án B sai. Chọn B. Câu hỏi 12 : Cho hình chữ nhật ABCD có cạnh \(AB = 4a\) và \(AD = 3a\). Tính \(T = \left| {\overrightarrow {AD} - \overrightarrow {AB} } \right|.\)
Đáp án: D Phương pháp giải: Sử dụng quy tắc cộng, trừ vectơ và định lý Py-ta-go. Lời giải chi tiết: \(T = \left| {\overrightarrow {AD} - \overrightarrow {AB} } \right| = \left| {\overrightarrow {BD} } \right| = BD = \sqrt {{{\left( {3a} \right)}^2} + {{\left( {4a} \right)}^2}} = 5a.\) Chọn D. Câu hỏi 13 : Cho tam giác\(ABC\), với \(M,{\rm{ }}N,{\rm{ }}P\)lần lượt là trung điểm của \(BC,{\rm{ }}CA,{\rm{ }}AB.\) Tìm câu sai:
Đáp án: D Phương pháp giải: Áp dụng tính chất trung điểm và quy tắc cộng Lời giải chi tiết: Ta có M là trung điểm của BC \( \Rightarrow \overrightarrow {MC} = \overrightarrow {BM} \) \( \Rightarrow \overrightarrow {PB} + \overrightarrow {MC} = \overrightarrow {PB} + \overrightarrow {BM} = \overrightarrow {PM} = - \overrightarrow {MP} \) Vậy D sai. Chọn D. Câu hỏi 14 : Cho góc \(Oxy\). Trên Ox, Oy lấy hai điểm A, B . Tìm điều kiện của A,B sao cho \(\overrightarrow {OA} + \overrightarrow {OB} \) nằm trên phân giác của góc \(Oxy\).
Đáp án: A Phương pháp giải: Áp dụng quy tác hình bình hành. Lời giải chi tiết: Dựng hình bình hành OACB. Khi đó: \(\overrightarrow {OA} + \overrightarrow {OB} = \overrightarrow {OD} \) Vậy \(\overrightarrow {OD} \) nằm trên phân giác góc \(xOy \Leftrightarrow OACB\) là hình thoi \( \Leftrightarrow OA = OB\). Chọn A. Câu hỏi 15 : Cho hình thoi \(ABCD\) cạnh a và \(\angle BCD = {60^0}\). Gọi O là tâm hình thoi. Tính \(\left| {\overrightarrow {AB} + \overrightarrow {AD} } \right|,\,\,\left| {\overrightarrow {OB} - \overrightarrow {DC} } \right|\).
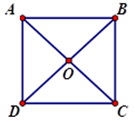
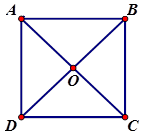
Đáp án: C Phương pháp giải: Áp dụng quy tắc cộng, trừ vectơ. Lời giải chi tiết: Ta có \(\left| {\overrightarrow {AB} + \overrightarrow {AD} } \right| = \left| {\overrightarrow {AC} } \right| = 2a\cos {30^0} = a\sqrt 3 ,\) \(\,\,\left| {\overrightarrow {OB} - \overrightarrow {DC} } \right| = \left| {\overrightarrow {DO} - \overrightarrow {DC} } \right| = \left| {\overrightarrow {CO} } \right| = a\cos {60^0} = \,\,\frac{{a\sqrt 3 }}{2}\) Chọn C. Câu hỏi 16 : Cho hình vuông \(ABCD\) có tâm là \(O\) và cạnh \(a\). Tính \(\left| {\overrightarrow {AB} + \overrightarrow {OD} } \right|,\,\,\left| {\overrightarrow {AB} - \overrightarrow {OC} + \overrightarrow {OD} } \right|\)
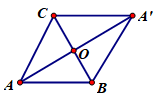
Đáp án: A Phương pháp giải: Áp dụng quy tắc cộng, trừ vectơ. Lời giải chi tiết: Ta có: \(\overrightarrow {OD} = \overrightarrow {BO} \Rightarrow \overrightarrow {AB} + \overrightarrow {OD} = \overrightarrow {AB} + \overrightarrow {BO} = \overrightarrow {AO} \) \( \Rightarrow \left| {\overrightarrow {AB} + \overrightarrow {OD} } \right| = AO = \frac{{AC}}{2} = \frac{{a\sqrt 2 }}{2}\) Ta có \(\overrightarrow {OC} = \overrightarrow {AO} \) \(\begin{array}{l} \Rightarrow \overrightarrow {AB} - \overrightarrow {OC} + \overrightarrow {OD} = \overrightarrow {AB} - \overrightarrow {AO} + \overrightarrow {OD} = \overrightarrow {OB} + \overrightarrow {OD} = \overrightarrow 0 \\ \Rightarrow \left| {\overrightarrow {AB} - \overrightarrow {OC} + \overrightarrow {OD} } \right| = 0.\end{array}\) Chọn A. Câu hỏi 17 : Cho tam giác \(ABC\) đều cạnh \(a\). Tính độ dài của các vectơ sau \(\overrightarrow {AB} - \overrightarrow {AC} ,\,\,\overrightarrow {AB} + \overrightarrow {AC} \).
Đáp án: C Phương pháp giải: Áp dụng quy tắc trừ và quy tắc hình bình hành Lời giải chi tiết: Theo quy tắc trừ ta có \(\overrightarrow {AB} - \overrightarrow {AC} = \overrightarrow {CB} \Rightarrow \left| {\overrightarrow {AB} - \overrightarrow {AC} } \right| = BC = a\) Gọi \(A'\) là đỉnh của hình bình hành \(ABA'C\) và \(O\) là tâm hình nình hành đó. Khi đó ta có \(\overrightarrow {AB} + \overrightarrow {AC} = \overrightarrow {AA'} \). Ta có: \(AO = \sqrt {A{B^2} - O{B^2}} = \sqrt {{a^2} - \frac{{{a^2}}}{4}} = \frac{{a\sqrt 3 }}{2}\) \( \Rightarrow \left| {\overrightarrow {AB} + \overrightarrow {AC} } \right| = AA' = 2AO = a\sqrt 3 \) Chọn C. Câu hỏi 18 : Cho hình chữ nhật \(ABCD\)có\(AB = 3,BC = 4.\) Độ dài của \(\overrightarrow {AC} \) là:
Đáp án: A Phương pháp giải: \(\left| {\overrightarrow {AC} } \right| = AC\) Lời giải chi tiết: Áp dụng định lý Pytago ta có: \(\left| {\overrightarrow {AC} } \right| = AC = \sqrt {A{B^2} + A{D^2}} = 5\) Chọn A. Câu hỏi 19 : Cho ba điểm phân biệt \(A,\)\(B,\)\(C.\) Đẳng thức nào đúng?
Đáp án: C Phương pháp giải: Áp dụng quy tắc cộng vecto. Lời giải chi tiết: Theo quy tắc cộng ta có: \(\overrightarrow {AB} + \overrightarrow {CA} = \overrightarrow {CA} + \overrightarrow {AB} = \overrightarrow {CB} .\) Chọn C. Câu hỏi 20 : Điều kiện nào là điều kiện cần và đủ để \(I\) là trung điểm của đoạn thẳng \(AB.\)
Đáp án: B Phương pháp giải: Sử dụng tính chất trung điểm. Lời giải chi tiết: I là trung điểm của AB \( \Leftrightarrow \overrightarrow {IA} = \overrightarrow {BI} \Leftrightarrow \overrightarrow {IA} = - \overrightarrow {IB} \Leftrightarrow \overrightarrow {IA} + \overrightarrow {IB} = \overrightarrow 0 \) Chọn B. Câu hỏi 21 : Cho tam giác\(ABC\), với \(M\) là trung điểm của \(BC.\) Tìm câu đúng:
Đáp án: A Phương pháp giải: Áp dụng quy tắc cộng vectơ. Lời giải chi tiết: Ta có: \(\overrightarrow {AM} + \overrightarrow {MB} + \overrightarrow {BA} = \overrightarrow {AA} = \overrightarrow 0 \) Chọn A. Câu hỏi 22 : Gọi \(O\) là tâm của hình vuông \(ABCD.\) Vectơ nào trong các vectơ dưới đây bằng \(\overrightarrow {CA} \)?
Đáp án: C Phương pháp giải: Áp dụng quy tắc cộng vectơ. Lời giải chi tiết: Ta có : \(\overrightarrow {BA} + \overrightarrow {DA} = \overrightarrow {CD} + \overrightarrow {DA} = \overrightarrow {CA} \) Chọn C. Câu hỏi 23 : Cho tam giác ABC với trọng tâm G. Gọi M là trung điểm AB. Chọn mệnh đề sai trong các mệnh đề sau:
Đáp án: B Phương pháp giải: M là trung điểm của AB \( \Rightarrow \overrightarrow {MA} + \overrightarrow {MB} = \overrightarrow 0 \) G là trọng tâm tam giác ABC \( \Rightarrow \overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GC} = \overrightarrow 0 \) và \(\overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} = 3\overrightarrow {OG} \) với O là điểm bất kì. Lời giải chi tiết: G là trọng tâm tam giác ABC \( \Rightarrow \overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GC} = \overrightarrow 0 \) Chọn B. Câu hỏi 24 : Biết điểm G là trọng tâm tam giác ABC. Mệnh đề nào sau đây đúng?
Đáp án: B Phương pháp giải: G là trọng tâm của tam giác ABC \( \Rightarrow \overrightarrow {AG} + \overrightarrow {BG} + \overrightarrow {CG} = \overrightarrow 0 .\) Lời giải chi tiết: G là trọng tâm của tam giác ABC \( \Rightarrow \overrightarrow {AG} + \overrightarrow {BG} + \overrightarrow {CG} = \overrightarrow 0 .\) \( \Rightarrow \overrightarrow {CG} = - \overrightarrow {AG} - \overrightarrow {BG} = \overrightarrow {GA} + \overrightarrow {GB} \) Chọn B. Câu hỏi 25 : Cho tam giác ABC. Tập hợp điểm M thỏa mãn \(\left| {\overrightarrow {MA} + \overrightarrow {MB} } \right| = 2\left| {\overrightarrow {AC} } \right|\) là
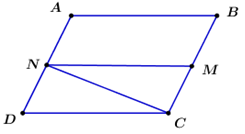
Đáp án: B Phương pháp giải: +) Dự đoán đáp án và chứng minh. +) Sử dụng công thức trung điểm. Lời giải chi tiết: \(\left| {\overrightarrow {MA} + \overrightarrow {MB} } \right| = 2\left| {\overrightarrow {AC} } \right|\) Gọi I là trung điểm của AB \( \Rightarrow \overrightarrow {MA} + \overrightarrow {MB} = 2\overrightarrow {MI} \Rightarrow \left| {\overrightarrow {MA} + \overrightarrow {MB} } \right| = 2\left| {\overrightarrow {MI} } \right|\) Để \(\left| {\overrightarrow {MA} + \overrightarrow {MB} } \right| = 2\left| {\overrightarrow {AC} } \right| \Leftrightarrow \left| {\overrightarrow {AC} } \right| = \left| {\overrightarrow {MI} } \right| \Leftrightarrow AC = MI\) Vậy tập hợp điểm M thỏa mãn \(\left| {\overrightarrow {MA} + \overrightarrow {MB} } \right| = 2\left| {\overrightarrow {AC} } \right|\) là đường tròn tâm I bán kính \(R = AC\) với I là trung điểm AB Chọn B. Câu hỏi 26 : Cho hình bình hành ABCD. Gọi M, N lần lượt là trung điểm BC và AD. Tổng của \(\overrightarrow {NC} \) và \(\overrightarrow {MC} \) là:
Đáp án: D Phương pháp giải: Dựa vào tính chất hình bình hành và quy tắc 3 điểm. Lời giải chi tiết: \(\overrightarrow {NC} + \overrightarrow {MC} = \overrightarrow {NA} + \overrightarrow {AC} + \overrightarrow {MC} = \left( {\overrightarrow {NA} + \overrightarrow {MC} } \right) + \overrightarrow {AC} = \overrightarrow {AC} \) Chọn D. Câu hỏi 27 : Cho 4 điểm A, B, C, D. Hãy tính \(\overrightarrow {AB} - \overrightarrow {AC} + \overrightarrow {BD} \).
Đáp án: D Phương pháp giải: Áp dụng quy tắc ba điểm. Lời giải chi tiết: \(\overrightarrow {AB} - \overrightarrow {AC} + \overrightarrow {BD} = \overrightarrow {CB} + \overrightarrow {BD} = \overrightarrow {CD} \) Chọn D. Câu hỏi 28 : Cho tam giác \(ABC\) vuông tại \(A\) có \(BC = a\sqrt 5 \). Tính độ dài của các vectơ \(\overrightarrow {AB} + \overrightarrow {AC} \).
Đáp án: B Phương pháp giải: Áp dụng quy tắc hình bình hành để tính. Lời giải chi tiết: Gọi \(D\) là điểm sao cho tứ giác \(ABDC\) là hình bình hành. Khi đó theo quy tắc hình bình hành ta có \(\overrightarrow {AB} + \overrightarrow {AC} = \overrightarrow {AD} \) Vì tam giác \(ABC\) vuông ở \(A\) nên tứ giác \(ABDC\) là hình chữ nhật suy ra \(AD = BC = a\sqrt 5 \) Vậy \(\left| {\overrightarrow {AB} + \overrightarrow {AC} } \right| = \left| {\overrightarrow {AD} } \right| = AD = a\sqrt 5 \) Chọn B. Câu hỏi 29 : Cho hình vuông \(ABCD\) có tâm là \(O\) và cạnh \(a\). Tính \(\left| {\overrightarrow {AB} + \overrightarrow {AD} } \right|,\,\,\left| {\overrightarrow {OA} - \overrightarrow {CB} } \right|,\,\,\left| {\overrightarrow {CD} - \overrightarrow {DA} } \right|\)
Đáp án: D Phương pháp giải: Áp dụng quy tắc hình bình hành, quy tắc cộng trừ để tính. Lời giải chi tiết: + Theo quy tắc hình bình hành ta có \(\overrightarrow {AB} + \overrightarrow {AD} = \overrightarrow {AC} \) Suy ra \(\left| {\overrightarrow {AB} + \overrightarrow {AD} } \right| = \left| {\overrightarrow {AC} } \right| = AC\). Áp dụng định lí Pitago ta có \(A{C^2} = A{B^2} + B{C^2} = 2{a^2} \Rightarrow AC = \sqrt 2 a\) Vậy \(\left| {\overrightarrow {AB} + \overrightarrow {AD} } \right| = a\sqrt 2 \) + Vì O là tâm của hình vuông nên \(\overrightarrow {OA} = \overrightarrow {CO} \Rightarrow \overrightarrow {OA} - \overrightarrow {CB} = \overrightarrow {CO} - \overrightarrow {CB} = \overrightarrow {BO} \) Vậy \(\left| {\overrightarrow {OA} - \overrightarrow {CB} } \right| = \left| {\overrightarrow {BO} } \right| = BO = {1 \over 2}BD = {1 \over 2}AC = {{a\sqrt 2 } \over 2}.\) + Do \(ABCD\) là hình vuông nên \(\overrightarrow {CD} = \overrightarrow {BA} \Rightarrow \overrightarrow {CD} - \overrightarrow {DA} = \overrightarrow {BA} + \overrightarrow {AD} = \overrightarrow {BD} \) Mà \(\left| {\overrightarrow {BD} } \right| = BD = \sqrt {A{B^2} + A{D^2}} = a\sqrt 2 \) suy ra \(\left| {\overrightarrow {CD} - \overrightarrow {DA} } \right| = a\sqrt 2 \) Chọn D. Câu hỏi 30 : Cho hình vuông \(ABCD\) có tâm là \(O\) và cạnh \(a\). \(M\) là một điểm bất kỳ. Tính độ dài vectơ \(\overrightarrow {MA} - \overrightarrow {MB} - \overrightarrow {MC} + \overrightarrow {MD} \)
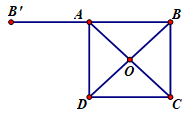
Đáp án: C Phương pháp giải: Lấy\(B'\) là điểm đối xứng của \(B\) qua \(A\). Áp dụng quy tắc trừ để tính. Lời giải chi tiết: Áp dụng quy tắc trừ ta có: \(\overrightarrow {MA} - \overrightarrow {MB} - \overrightarrow {MC} + \overrightarrow {MD} = \left( {\overrightarrow {MA} - \overrightarrow {MB} } \right) - \left( {\overrightarrow {MC} - \overrightarrow {MD} } \right) = \overrightarrow {BA} - \overrightarrow {DC} = \overrightarrow {BA} - \overrightarrow {DC} \) Lấy\(B'\) là điểm đối xứng của \(B\) qua \(A\) Khi đó \( - \overrightarrow {DC} = \overrightarrow {AB'} \Rightarrow \overrightarrow {BA} - \overrightarrow {DC} = \overrightarrow {BA} + \overrightarrow {AB'} = \overrightarrow {BB'} \) \( \Rightarrow \left| {\overrightarrow {MA} - \overrightarrow {MB} - \overrightarrow {MC} + \overrightarrow {MD} } \right| = \left| {\overrightarrow {BB'} } \right| = BB' = 2a\) Chọn C. Câu hỏi 31 : Cho bốn điểm A, B, C, O phân biệt có độ dài ba vectơ \(\overrightarrow {OA} ,\,\,\overrightarrow {OB} ,\,\,\overrightarrow {OC} \) cùng bằng \(a\) và \(\overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} = \overrightarrow 0 \). Tính \(\left| {\overrightarrow {OB} + \overrightarrow {AC} - \overrightarrow {OA} } \right|\)
Đáp án: A Phương pháp giải: Chứng minh \(\Delta ABC\) đều. Gọi I là trung điểm BC. Tính theo \(\overrightarrow {AI} \) Lời giải chi tiết: Từ giả thiết suy ra ba điểm A, B, C tạo thành tam giác đều nhận O làm trọng tâm Gọi I là trung điểm BC. \(\Delta ABC\) đều nên \(AI = \frac{{\sqrt 3 }}{2}a\) \(\left| {\overrightarrow {OB} + \overrightarrow {AC} - \overrightarrow {OA} } \right| = \left| {\overrightarrow {AB} + \overrightarrow {AC} } \right| = 2\left| {\overrightarrow {AI} } \right| = a\sqrt 3 \) Chọn A. Câu hỏi 32 : Cho năm điểm \(A,\,B,\,C,\,D,\,E\). Khẳng định nào đúng?
Đáp án: D Phương pháp giải: Áp dụng quy tác hình bình hành. Lời giải chi tiết: Biến đổi vế trái ta có \(\begin{array}{l}VT = \left( {\overrightarrow {AC} + \overrightarrow {CB} } \right) + \overrightarrow {CD} + \left( {\overrightarrow {ED} + \overrightarrow {DA} } \right)\\\,\,\,\,\,\,\, = \left( {\overrightarrow {CB} + \overrightarrow {ED} } \right) + \left( {\overrightarrow {AC} + \overrightarrow {CD} } \right) + \overrightarrow {DA} \\\,\,\,\,\,\,\, = \left( {\overrightarrow {CB} + \overrightarrow {ED} } \right) + \overrightarrow {AD} + \overrightarrow {DA} \\\,\,\,\,\,\,\, = \overrightarrow {CB} + \overrightarrow {ED} \end{array}\) Chọn D. Câu hỏi 33 : Cho hình bình hành \(ABCD\) tâm \(O\). M là một điểm bất kì trong mặt phẳng. Khẳng định nào sau đây là đúng nhất?
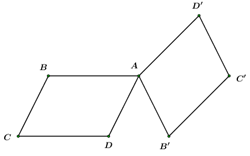
Đáp án: A Phương pháp giải: Áp dụng quy tắc hình bình hành. Lời giải chi tiết: Ta có: \(\overrightarrow {BA} + \overrightarrow {DA} + \overrightarrow {AC} = - \overrightarrow {AB} - \overrightarrow {AD} + \overrightarrow {AC} = - \left( {\overrightarrow {AB} + \overrightarrow {AD} } \right) + \overrightarrow {AC} .\) Theo quy tắc hình bình hành ta có \(\overrightarrow {AB} + \overrightarrow {AD} = \overrightarrow {AC} \) \( \Rightarrow \overrightarrow {BA} + \overrightarrow {DA} + \overrightarrow {AC} = - \overrightarrow {AC} + \overrightarrow {AC} = \overrightarrow 0 \) Chọn A. Câu hỏi 34 : Cho hai hình bình hành \(ABCD\) và \(AB'C'D'\) có chung đỉnh A. Khẳng định nào đúng
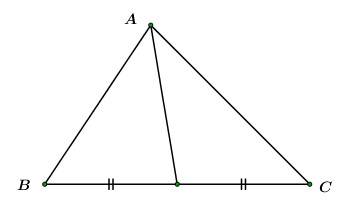
Đáp án: B Phương pháp giải: Sử dụng quy tắc trừ và quy tắc hình bình hành để tách và nhóm cho phù hợp. Lời giải chi tiết: Theo quy tắc trừ và quy tắc hình bình hành ta có: \(\begin{array}{l}\overrightarrow {B'B} + \overrightarrow {CC'} + \overrightarrow {D'D} = \left( {\overrightarrow {AB} - \overrightarrow {AB'} } \right) + \left( {\overrightarrow {AC'} - \overrightarrow {AC} } \right) + \left( {\overrightarrow {AD} - \overrightarrow {AD'} } \right)\\ = \left( {\overrightarrow {AB} + \overrightarrow {AD} } \right) - \overrightarrow {AC} - \left( {\overrightarrow {AB'} + \overrightarrow {AD} '} \right) + \overrightarrow {AC'} = \overrightarrow 0 \end{array}\) Chọn B. Câu hỏi 35 : Cho tam giác \(ABC\) vuông tại \(A\) có \(AB{\rm{ = 2,}}\,AC = 4.\) Giá trị của \(\left| {2.\overrightarrow {AB} + \overrightarrow {AC} } \right|\) bằng
Đáp án: A Phương pháp giải: Vẽ hình, xác định vectơ bài cho rồi tính độ dài vecto bài yêu cầu. Lời giải chi tiết: Dựng \(D\) sao cho \(2\overrightarrow {AB} = \overrightarrow {AD} \). Khi đó, \(\left| {\overrightarrow {AC} } \right| = \left| {\overrightarrow {AD} } \right| = 4\) nên \(\Delta ACD\) là tam giác vuông cân tại \(D\) Dựng \(E\) sao cho tứ giác \(ACED\) là hình vuông. Khi đó \(\left| {2\overrightarrow {AB} + \overrightarrow {AC} } \right| = \left| {\overrightarrow {AD} + \overrightarrow {AC} } \right| = \left| {\overrightarrow {AE} } \right| = AE = CD\) Mà \(C{D^2} = 2A{C^2} = {2.4^2} = 32 \Rightarrow CD = 4\sqrt 2 \) Chọn A. Câu hỏi 36 : Cho tam giác \(ABC,\) gọi \(M\) là trung điểm của \(BC,\) điểm \(I\) thỏa mãn \(2\overrightarrow {IA} + \overrightarrow {IB} + \overrightarrow {IC} = \overrightarrow 0 .\) Chứng minh \(I\) là trung điểm của \(AM\). Phương pháp giải: Sử dụng qui tắc trung điểm và qui tắc cộng véc tơ Lời giải chi tiết: Vì \(M\) là trung điểm của \(BC\) nên \(\overrightarrow {MB} + \overrightarrow {MC} = \overrightarrow 0 \) Ta có : \(2\overrightarrow {IA} + \overrightarrow {IB} + \overrightarrow {IC} = \overrightarrow 0 \) \(\begin{array}{l} \Leftrightarrow 2\overrightarrow {IA} + \overrightarrow {IM} + \overrightarrow {MA} + \overrightarrow {IM} + \overrightarrow {MB} = \overrightarrow 0 \\ \Leftrightarrow 2\left( {\overrightarrow {IA} + \overrightarrow {IB} } \right) = \overrightarrow 0 \\ \Leftrightarrow \overrightarrow {IA} + \overrightarrow {IB} = \overrightarrow 0 \\ \Leftrightarrow \overrightarrow {IA} = \overrightarrow {BI} \end{array}\) Nên \(I\) là trung điểm của \(AB.\) Câu hỏi 37 : Cho tam giác \(ABC.\) Tìm tập hợp các điểm \(M\) thỏa mãn \(\left| {\overrightarrow {MB} - \overrightarrow {MC} } \right| = \left| {\overrightarrow {BM} - \overrightarrow {BA} } \right|.\)
Đáp án: A Phương pháp giải: Thu gọn các véc tơ ở đẳng thức bài cho và nhận xét. Lời giải chi tiết: Ta có: \(\left| {\overrightarrow {MB} - \overrightarrow {MC} } \right| = \left| {\overrightarrow {BM} - \overrightarrow {BA} } \right|\) \( \Leftrightarrow \left| {\overrightarrow {CB} } \right| = \left| {\overrightarrow {AM} } \right| \Leftrightarrow BC = AM\) Do đó điểm \(M\) luôn cách điểm \(A\) một khoảng \(BC\) cố định. Vậy \(M\) nằm trên đường tròn tâm \(A\) bán kính \(BC\). Chọn A. Câu hỏi 38 : Cho hình vuông \(ABCD\) cạnh bằng \(a,\) tâm \(O.\) Tính \(\left| {\overrightarrow {AO} + \overrightarrow {AB} } \right|.\)
Đáp án: A Phương pháp giải: Tính \(\overrightarrow {AO} + \overrightarrow {AB} \) và suy ra độ dài. Lời giải chi tiết: Gọi \(E\) là trung điểm của \(OB\). Khi đó \(\overrightarrow {AO} + \overrightarrow {AB} = 2\overrightarrow {AE} \). \(\Delta ABC\) vuông cân tại \(B\) có \(AB = BC = a\) nên \(AC = \sqrt {A{B^2} + B{C^2}} \) \( = \sqrt {{a^2} + {a^2}} = a\sqrt 2 \) \( \Rightarrow AO = OB = \frac{1}{2}AC = \frac{{a\sqrt 2 }}{2}\) \( \Rightarrow OE = \frac{1}{2}OB = \frac{1}{2}.\frac{{a\sqrt 2 }}{2} = \frac{{a\sqrt 2 }}{4}\) Tam giác \(AOE\) vuông tại \(O\) có \(AE = \sqrt {A{O^2} + O{E^2}} \) \( = \sqrt {\frac{{2{a^2}}}{4} + \frac{{2{a^2}}}{{16}}} = \frac{{a\sqrt {10} }}{4}\) Vậy \(\left| {\overrightarrow {AO} + \overrightarrow {AB} } \right| = 2\left| {\overrightarrow {AE} } \right| = 2AE\)\( = 2.\frac{{a\sqrt {10} }}{4} = \frac{{a\sqrt {10} }}{2}\) Chọn A. Câu hỏi 39 : Cho hình vuông \(ABCD\) có tâm là \(O\) và cạnh \(a\). \(M\) là một điểm bất kỳ. Tính độ dài vectơ \(\overrightarrow u = \overrightarrow {MA} + \overrightarrow {MB} - \overrightarrow {MC} - \overrightarrow {MD} \).
Đáp án: A Phương pháp giải: Chứng minh \(\overrightarrow u \) không phụ thuộc vị trí điểm \(M\)và tính theo quy tắc hình bình hành. Lời giải chi tiết: Theo quy tắc phép trừ ta có: \(\overrightarrow u = \left( {\overrightarrow {MA} - \overrightarrow {MC} } \right) + \left( {\overrightarrow {MB} - \overrightarrow {MD} } \right) = \overrightarrow {CA} + \overrightarrow {DB} \) Suy ra \(\overrightarrow u \) không phụ thuộc vị trí điểm \(M\). Qua \(A\) kẻ đường thẳng song song với \(DB\) cắt \(BC\) tại \(C'\). Khi đó tứ giác \(ADBC'\) là hình bình hành (vì có cặp cạnh đối song song) suy ra \(\overrightarrow {DB} = \overrightarrow {AC'} \) Do đó \(\overrightarrow u = \overrightarrow {CA} + \overrightarrow {AC'} = \overrightarrow {CC'} \) Vì vậy \(\left| {\overrightarrow u } \right| = \left| {\overrightarrow {CC'} } \right| = BC + BC' = a + a = 2a\) Chọn A. Câu hỏi 40 : Cho tam giác \(ABC\). Gọi M, N, P lần lượt là trung điểm của \(BC,\,\,CA,\,\,AB\). \(O\) là điểm bất kì. Khẳng định nào sau đây là đúng nhất?
Đáp án: D Phương pháp giải: Chứng minh \(\overrightarrow {BM} + \overrightarrow {CN} + \overrightarrow {AP} = \overrightarrow 0 \), từ đó sử dụng quy tắc cộng để tách và nhóm cho phù hợp. Lời giải chi tiết: Vì \(PN,\,MN\) là đường trung bình của tam giác \(ABC\) nên \(PN//BM,\,\,MN//BP\) suy ra tứ giác \(BMNP\) là hình bình hành \( \Rightarrow \overrightarrow {BM} = \overrightarrow {PN} \) \(N\) là trung điểm của \(AC \Rightarrow \overrightarrow {CN} = \overrightarrow {NA} \) Do đó theo quy tắc ba điểm ta có \(\begin{array}{l}\overrightarrow {BM} + \overrightarrow {CN} + \overrightarrow {AP} = \left( {\overrightarrow {PN} + \overrightarrow {NA} } \right) + \overrightarrow {AP} \\ = \overrightarrow {PA} + \overrightarrow {AP} = \overrightarrow 0 \end{array}\) Theo quy tắc ba điểm ta có \(\begin{array}{l}\overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} = \left( {\overrightarrow {OP} + \overrightarrow {PA} } \right) + \left( {\overrightarrow {OM} + \overrightarrow {MB} } \right) + \left( {\overrightarrow {ON} + \overrightarrow {NC} } \right)\\ = \left( {\overrightarrow {OM} + \overrightarrow {ON} + \overrightarrow {OP} } \right) + \overrightarrow {PA} + \overrightarrow {MB} + \overrightarrow {NC} \\ = \left( {\overrightarrow {OM} + \overrightarrow {ON} + \overrightarrow {OP} } \right) - \left( {\overrightarrow {BM} + \overrightarrow {CN} + \overrightarrow {AP} } \right)\end{array}\) Mà \(\overrightarrow {BM} + \overrightarrow {CN} + \overrightarrow {AP} = \overrightarrow 0 \) suy ra \(\overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} = \overrightarrow {OM} + \overrightarrow {ON} + \overrightarrow {OP} \). Chọn D. Quảng cáo
|