30 bài tập về Giá trị lượng giác của một góc bất kỳ từ 0 độ đến 180 độLàm bàiQuảng cáo
Câu hỏi 1 : Trong các đẳng thức sau đây, đẳng thức nào đúng?
Đáp án: C Phương pháp giải: Sử dụng bảng giá trị lượng giác các góc đặc biệt. Lời giải chi tiết: Vì \(\alpha = {150^0}\) là góc tù nên \(\sin \alpha > 0,\cos \alpha < 0,\tan \alpha = {{\sin \alpha } \over {c{\rm{os}}\alpha }} < 0,\cot \alpha < 0.\) Do đó các đáp án A, B, D đều sai. Ta chỉ xét đáp án C. Ta có \(\tan {150^ \circ } = - \tan {30^ \circ } = - {1 \over {\sqrt 3 }}.\) Chọn C. Câu hỏi 2 : Tính giá trị biểu thức \(P = \sin {30^0}\cos {60^0} + \sin {60^0}\cos {30^0}.\)
Đáp án: A Phương pháp giải: Tính giá trị của biểu thức. Lời giải chi tiết: \(P = \sin {30^0}\cos {60^0} + \sin {60^0}\cos {30^0}. = \dfrac{1}{2}.\dfrac{1}{2} + \dfrac{{\sqrt 3 }}{2}.\dfrac{{\sqrt 3 }}{2} = \dfrac{1}{4} + \dfrac{3}{4} = 1\) Chọn A. Câu hỏi 3 : Góc \(\frac{{7\pi }}{6}\) có số đo bằng độ là:
Đáp án: D Phương pháp giải: \(\pi = {180^o}.\) Lời giải chi tiết: \(\frac{{7\pi }}{6} = \frac{{{{7.180}^o}}}{6} = {210^o}\) Chọn D. Câu hỏi 4 : Mệnh đề nào sau đây là đúng?
Đáp án: C Phương pháp giải: \(\pi \) rad \( = {180^o}\) Lời giải chi tiết: Ta có: \(\pi \) rad \( = {180^o}\) Vậy C đúng Chọn C. Câu hỏi 5 : Số đo theo đợn vị radian của góc \({315^o}\) là :
Đáp án: B Phương pháp giải: \(\pi = {180^o}\) Lời giải chi tiết: \({315^o} = \frac{{315\pi }}{{180}} = \frac{{7\pi }}{4}\) Chọn B. Câu hỏi 6 : Giá trị của biểu thức \(P = c{\rm{os3}}{{\rm{0}}^o}{\rm{cos6}}{{\rm{0}}^o} - \sin {30^o}\sin {60^o}?\)
Đáp án: D Phương pháp giải: Nắm được bảng giá trị lượng giác của một số góc đặc biệt như \({30^o};{45^o};{60^o};{90^o};...\) Cách 2: Với \(\angle B + \angle C = {90^o} \Rightarrow \left\{ \begin{array}{l}\sin \angle B = \cos \angle C\\\cos \angle B = \sin \angle C\end{array} \right..\) Lời giải chi tiết: Ta có: \(P = \cos {30^o}.\cos {60^o} - \sin {30^o}.\sin {60^o} = \frac{{\sqrt 3 }}{2}.\frac{1}{2} - \frac{1}{2}.\frac{{\sqrt 3 }}{2} = 0\) Cách 2: \(P = \cos {30^o}.\cos {60^o} - \sin {30^o}.\sin {60^o} = \cos {30^o}.\cos {60^o} - \cos {60^o}.\cos {30^0} = 0.\) Chọn D. Câu hỏi 7 : Trong tam giác \(ABC\) vuông ở \(A\) có góc \(\angle B = {30^o}.\) Khẳng định nào sau đây là sai?
Đáp án: A Phương pháp giải: Cho tam giác \(ABC\) vuông ở \(A.\) Khi đó, \(\angle B + \angle C = {90^o} \Rightarrow \left\{ \begin{array}{l}\sin \angle B = \cos \angle C\\\cos \angle B = \sin \angle C\end{array} \right.\) Nắm được giá trị lượng giác của một số góc đặc biệt như \({30^o};\,\,{45^o};\,\,\,{60^o};\,\,{90^o};.....\) Lời giải chi tiết: \(\Delta ABC\) vuông tại \(A \Rightarrow \angle B + \angle C = {90^0} \Rightarrow \angle C = {90^0} - \angle B = {90^0} - {30^0} = {60^0}.\) \( \Rightarrow \left\{ \begin{array}{l}\sin \angle C = \sin {60^0} = \frac{{\sqrt 3 }}{2};\,\,\,\cos \angle C = \cos {60^0} = \frac{1}{2}\\\tan \angle C = \tan {60^0} = \sqrt 3 ;\,\,\,\cot \angle C = \cot {60^0} = \frac{1}{{\sqrt 3 }}\end{array} \right..\) Chọn A. Câu hỏi 8 : Cho \(\alpha \) là góc tù. Khẳng định nào sau đây là sai?
Đáp án: B Phương pháp giải: Khi góc \(\alpha \) tù thì \(\sin \alpha > 0,\cos \alpha < 0,\tan \alpha < 0,\cot \alpha < 0.\) Lời giải chi tiết: Khi góc \(\alpha \) tù thì \(\sin \alpha > 0,\cos \alpha < 0,\tan \alpha < 0,\cot \alpha < 0.\) Chọn B. Câu hỏi 9 : Cho hệ thức đúng được suy ra từ hệ thức \({\rm{co}}{{\rm{s}}^2}\alpha + {\sin ^2}\alpha = 1?\)
Đáp án: D Phương pháp giải: Với một góc \(\beta \) bất kì, ta luôn có: \({\rm{co}}{{\rm{s}}^2}\beta + {\sin ^2}\beta = 1.\) Lời giải chi tiết: Từ biểu thức: \({\rm{co}}{{\rm{s}}^2}\alpha + {\sin ^2}\alpha = 1,\) ta suy ra \({\rm{co}}{{\rm{s}}^2}\frac{\alpha }{5} + {\sin ^2}\frac{\alpha }{5} = 1 \Rightarrow 5\left( {{\rm{co}}{{\rm{s}}^2}\frac{\alpha }{5} + {{\sin }^2}\frac{\alpha }{5}} \right) = 5\) Chọn D. Câu hỏi 10 : Cho hai góc \(\alpha ,\beta \) thỏa mãn \(\alpha < \beta \) và \(90^\circ < \alpha ,\beta < 180^\circ .\) Tìm khẳng định đúng?
Đáp án: A Phương pháp giải: Sử dụng giá trị lượng giác của một cung. Lời giải chi tiết: Với \(\alpha < \beta \) và \(90^\circ < \alpha ,\beta < 180^\circ \) thì \(\cos \alpha > \cos \beta .\) Chọn A. Câu hỏi 11 : Cho góc \(0^\circ < \alpha < 90^\circ .\) Khẳng định nào sau đây sai?
Đáp án: B Phương pháp giải: Sử dụng đường tròn lượng giác để đánh giá các giá trị lượng giác của một góc. Lời giải chi tiết: Với \(0^\circ < \alpha < 90^\circ \) thì \(\cos \alpha > 0.\) Chọn B. Câu hỏi 12 : Giá trị của\(\tan \frac{\pi }{6}\) là
Đáp án: A Phương pháp giải: Bấm máy tính hoặc dùng bảng lượng giác. Lời giải chi tiết: Ta có: \(\tan \frac{\pi }{6} = \frac{{\sqrt 3 }}{3}\) Chọn A. Câu hỏi 13 : Biết \(\cot \alpha = 3\), khi đó giá trị của \(\sin \left( {2\alpha - \frac{\pi }{4}} \right)\) là:
Đáp án: C Phương pháp giải:
Sử dụng các công thức sau đây: \(\sin \left( {a - b} \right) = \sin a\cos b - \sin b\cos a;\,\,\frac{1}{{{{\sin }^2}a}} = 1 + {\cot ^2}a;\,\,\cos 2a = 1 - 2{\sin ^2}a;\,\,\cot 2a = \frac{{{{\cot }^2}a - 1}}{{2\cot a}}\) Lời giải chi tiết: \(\begin{array}{l}\sin \left( {2\alpha - \frac{\pi }{4}} \right) = \sin 2\alpha \cos \frac{\pi }{4} - \cos 2\alpha \sin \frac{\pi }{4} = \frac{{\sqrt 2 }}{2}\left( {\sin 2\alpha - \cos 2\alpha } \right)\\\cot \alpha = 3 \Rightarrow \frac{1}{{{{\sin }^2}\alpha }} = 1 + {\cot ^2}\alpha = 1 + {3^2} = 10\\ \Rightarrow \cos 2\alpha = 1 - 2{\sin ^2}\alpha = 1 - 2.\frac{1}{{10}} = \frac{4}{5}\\\cot 2\alpha = \frac{{{{\cot }^2}\alpha - 1}}{{2\cot \alpha }} = \frac{4}{3} \Rightarrow \sin 2\alpha = \frac{{\cos 2\alpha }}{{\cot 2\alpha }} = \frac{3}{5}\\ \Rightarrow \sin \left( {2\alpha - \frac{\pi }{4}} \right) = \frac{{\sqrt 2 }}{2}\left( {\frac{3}{5} - \frac{4}{5}} \right) = \frac{{ - \sqrt 2 }}{{10}}\end{array}\) Chọn C. Câu hỏi 14 : Cho tam giác ABC vuông tại A, góc B bằng 300. Khẳng định nào sau đây là sai?
Đáp án: A Phương pháp giải: Sử dụng bảng giá trị lượng giác các góc đặc biệt. Lời giải chi tiết: Tam giác ABC vuông tại A, \(\widehat B = {30^0} \Rightarrow \widehat C = {90^0} - {30^0} = {60^0}.\) Theo bảng giá trị lượng giác các góc đặc biệt \(\eqalign{ & \sin B = \sin {30^0} = \cos C = \cos {60^0} = {1 \over 2} \cr & \sin C = \sin 60 = \cos B = \cos 30 = {{\sqrt 3 } \over 2}. \cr} \) Vậy đáp án A sai. Chọn A. Câu hỏi 15 : Giá trị \(\sin \frac{{47\pi }}{6}\) bằng:
Đáp án: D Phương pháp giải: \(\sin \left( {x + k2\pi } \right) = \sin x\) Lời giải chi tiết: \(\sin \frac{{47\pi }}{6} = \sin \left( {8\pi - \frac{\pi }{6}} \right) = \sin \left( { - \frac{\pi }{6}} \right) = - \sin \frac{\pi }{6} = - \frac{1}{2}\) Chọn D. Câu hỏi 16 : Cung có số đo 2250 được đổi sang số đo rad là :
Đáp án: C Phương pháp giải: \(\pi \) rad \( = {180^o}\) Lời giải chi tiết: \({225^o} = \frac{{225\pi }}{{180}} = \frac{{5\pi }}{4}\) Chọn C. Câu hỏi 17 : Một đường tròn có bán kính \(R = 75cm\). Độ dài của cung trên đường tròn đó có số đo \(\alpha = \frac{\pi }{{25}}\) là:
Đáp án: A Phương pháp giải: Độ dài cung = bán kính \( \times n.\) Trong đó n là số đo góc chứa cung tính theo radian. Lời giải chi tiết: Độ dài cung có số đo \(\alpha = \frac{\pi }{{25}}\) là: \(R.\alpha = 75.\frac{\pi }{{25}} = 3\pi \;\;\left( {cm} \right).\) Chọn A. Câu hỏi 18 : Cho \(\sin \alpha = \frac{1}{3}.\)Tính giá trị biểu thức \(P = 3{\sin ^2}\alpha + {\cos ^2}\alpha .\)
Đáp án: C Phương pháp giải: Ta sử dụng công thức: \({\sin ^2}\alpha + {\cos ^2}\alpha = 1.\) Lời giải chi tiết: Ta có: \(P = 3{\sin ^2}\alpha + {\cos ^2}\alpha = 3{\sin ^2}\alpha + \left( {1 - {{\sin }^2}\alpha } \right) = 2{\sin ^2}\alpha + 1 = 2{\left( {\frac{1}{3}} \right)^2} + 1 = \frac{{11}}{9}.\) Chọn C. Câu hỏi 19 : Tam giác đều \(ABC\) có đường cao \(AH.\) Khẳng định nào sau đây là đúng?
Đáp án: B Phương pháp giải: Xác định số đo các góc, từ đó tính giá trị lượng giác của góc đã cho. Lời giải chi tiết: \(\Delta ABC\) là tam giác đều có đường cao \(AH \Rightarrow AH\) cùng là đường phân giác của \(\Delta ABC\) \( \Rightarrow \angle BAH = \angle HAC = {30^o} \Rightarrow \left\{ {\begin{array}{*{20}{c}}{\sin \angle BAH = \sin \angle HAC = \frac{1}{2}}\\{{\rm{cos}}\angle BAH = \frac{{\sqrt 3 }}{2}}\end{array} \Rightarrow } \right.\) loại A, C. Vì \(\angle ABC = {60^o} \Rightarrow \sin \angle ABC = \frac{{\sqrt 3 }}{2}.\) Chọn B Câu hỏi 20 : Cho \(\cos 15^\circ = \frac{{\sqrt 2 + \sqrt 6 }}{4}.\) Khẳng định nào sau đây đúng?
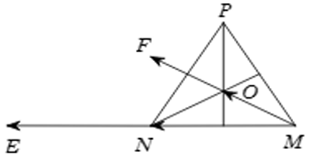
Đáp án: B Phương pháp giải: Áp dụng công thức: \(\cos \left( {\pi - x} \right) = - \cos x.\) Lời giải chi tiết: Ta có: \(\cos 165^\circ = - \cos \left( {180^\circ - 165^\circ } \right) = - \cos 15^\circ = - \frac{{\sqrt 2 + \sqrt 6 }}{4}.\) Chọn B. Câu hỏi 21 : Cho \(O\) là tâm đường tròn ngoại tiếp tam giác đều \(MNP.\) Góc nào sau đây bằng \({120^o}?\)
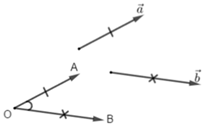
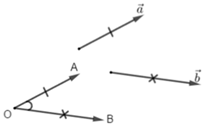
Đáp án: B Phương pháp giải: Cho hai vecto \(\overrightarrow a ,\,\,\overrightarrow b \ne \overrightarrow 0 .\) Từ \(O,\) vẽ \(\overrightarrow {OA} = \overrightarrow a ,\,\,\overrightarrow {OB} = \overrightarrow b \Rightarrow \angle AOB = \angle \left( {\overrightarrow a ,\,\,\overrightarrow b } \right).\) Lời giải chi tiết: Vẽ \(\overrightarrow {NE} = \overrightarrow {MN} .\) Khi đó \(\left( {\overrightarrow {MN} ,\overrightarrow {NP} } \right) = \left( {\overrightarrow {NE} ,\overrightarrow {NP} } \right) = \angle PNE = {180^o} - \angle MNP = {180^o} - {60^o} = {120^o}.\) Vẽ \(\overrightarrow {OF} = \overrightarrow {MO} \Rightarrow \left( {\overrightarrow {MO} ,\overrightarrow {ON} } \right) = \left( {\overrightarrow {OF} ,\overrightarrow {ON} } \right) = \angle NOF = {60^o}\) Vì \(MN \bot OP\,\, \Rightarrow \left( {\overrightarrow {MN} ,\overrightarrow {OP} } \right) = {90^o}\) Ta có \(\left( {\overrightarrow {MN} ,\overrightarrow {MP} } \right) = \angle NMP = {60^o}.\) Chọn B. Câu hỏi 22 : Cho biết \(\cot \alpha = 5.\) Giá trị của \(A = 2{\cos ^2}\alpha + 5\sin \alpha \cos \alpha + 1\)bằng bao nhiêu?
Đáp án: C Phương pháp giải: Ta sử dụng công thức sau: \(\tan \alpha = \frac{{\sin \alpha }}{{\cos \alpha }};\,\,\,\,1 + {\cot ^2}\alpha = \frac{1}{{{{\sin }^2}\alpha }}.\) Lời giải chi tiết: Ta có: \(\begin{array}{l}A = 2{\cos ^2}\alpha + 5\sin \alpha \cos \alpha + 1 = {\sin ^2}\alpha \left( {2\frac{{{{\cos }^2}\alpha }}{{{{\sin }^2}\alpha }} + 5\frac{{\cos \alpha }}{{\sin \alpha }} + \frac{1}{{{{\sin }^2}\alpha }}} \right)\\\,\,\,\,\, = \frac{1}{{1 + {{\cot }^2}\alpha }}\left( {2{{\cot }^2}\alpha + 5\cot \alpha + 1 + {{\cot }^2}\alpha } \right)\\\,\,\,\,\, = \frac{{3{{\cot }^2}\alpha + 5\cot \alpha + 1}}{{{{\cot }^2}\alpha + 1}} = \frac{{{{3.5}^2} + 5.5 + 1}}{{{5^2} + 1}} = \frac{{101}}{{26}}.\end{array}\) Chọn C Câu hỏi 23 : Cho biết \(2\cos \alpha + \sqrt 2 \sin \alpha = 2,{0^o} < \alpha < {90^o}.\) Tính giá trị của \(\cot \alpha .\)
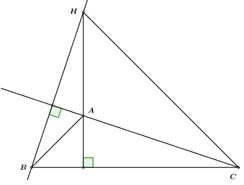
Đáp án: B Phương pháp giải: Sử dụng công thức: \(\cot \alpha = \frac{{\cos \alpha }}{{\sin \alpha }};\,\,\,{\cos ^2}\alpha + {\sin ^2}\alpha = 1.\) Lời giải chi tiết: Ta có: \(2\cos \alpha + \sqrt 2 \sin \alpha = 2 \Leftrightarrow \sqrt 2 \sin \alpha = 2 - 2\cos \alpha \) \(\begin{array}{l} \Leftrightarrow 2{\sin ^2}\alpha = {\left( {2 - 2\cos \alpha } \right)^2}\\ \Leftrightarrow 2 - 2{\cos ^2}\alpha = 4 - 8\cos \alpha + 4{\cos ^2}\alpha \\ \Leftrightarrow 6{\cos ^2}\alpha - 8\cos \alpha + 2 = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{\cos \alpha = 1}\\{\cos \alpha = \frac{1}{3}}\end{array}} \right.\end{array}\) + \(\cos \alpha = 1:\) không thoả mãn vì \({0^o} < \alpha < {90^o}.\) + \(\cos \alpha = \frac{1}{3} \Rightarrow \sin \alpha = \frac{{2\sqrt 2 }}{3} \Rightarrow \cot \alpha = \frac{{\cos \alpha }}{{\sin \alpha }} = \frac{{\sqrt 2 }}{4}.\) Chọn B. Câu hỏi 24 : Tam giác \(ABC\) có góc \(\angle A = {100^o}\) và có trực tâm \(H.\) Tính tổng \(\left( {\overrightarrow {HA} ,\overrightarrow {HB} } \right) + \left( {\overrightarrow {HB} ,\overrightarrow {HC} } \right) + \left( {\overrightarrow {HC} ,\overrightarrow {HA} } \right).\)
Đáp án: B Phương pháp giải: Cho hai vecto \(\overrightarrow a ,\,\,\overrightarrow b \ne \overrightarrow 0 .\) Từ \(O,\) vẽ \(\overrightarrow {OA} = \overrightarrow a ,\,\,\overrightarrow {OB} = \overrightarrow b \Rightarrow \angle AOB = \angle \left( {\overrightarrow a ,\,\,\overrightarrow b } \right).\) Lời giải chi tiết: Ta có: \(\left\{ {\begin{array}{*{20}{c}}{\left( {\overrightarrow {HA} ,\overrightarrow {HB} } \right) = \angle BHA}\\{\left( {\overrightarrow {HB} ,\overrightarrow {HC} } \right) = \angle BHC}\\{\left( {\overrightarrow {HC} ,\overrightarrow {HA} } \right) = \angle CHA}\end{array}} \right.\) \( \Rightarrow \left( {\overrightarrow {HA} ,\overrightarrow {HB} } \right) + \left( {\overrightarrow {HB} ,\overrightarrow {HC} } \right) + \left( {\overrightarrow {HC} ,\overrightarrow {HA} } \right) = \angle BHA + \angle BHC + \angle CHA = 2.\angle BHC = 2.\left( {{{180}^o} - {{100}^0}} \right) = {160^o}\) Chọn B. Câu hỏi 25 : Cho biết \(\cos \alpha + \sin \alpha = \frac{1}{3}.\) Giá trị của \(P = \sqrt {{{\tan }^2}\alpha + {{\cot }^2}\alpha } \) bằng bao nhiêu?
Đáp án: D Phương pháp giải: Áp dụng các công thức: \(\left\{ \begin{array}{l}1 + {\tan ^2}\alpha = \frac{1}{{{\rm{co}}{{\rm{s}}^2}\alpha }};\,\,\,\,1 + {\cot ^2}\alpha = \frac{1}{{{{\sin }^2}\alpha }}\\{\left( {\sin \alpha + \cos \alpha } \right)^2} = 1 + 2\sin \alpha \cos \alpha \end{array} \right..\) Lời giải chi tiết: Ta có: \(\cos \alpha + \sin \alpha = \frac{1}{3} \Rightarrow {\left( {\cos \alpha + \sin \alpha } \right)^2} = \frac{1}{9} \Leftrightarrow 1 + 2\sin \alpha \cos \alpha = \frac{1}{9} \Leftrightarrow \sin \alpha \cos \alpha = - \frac{4}{9}.\) \(\begin{array}{l} \Rightarrow P = \sqrt {{{\tan }^2}\alpha + {{\cot }^2}\alpha } = \sqrt {\frac{1}{{{{\cos }^2}\alpha }} - 1 + \frac{1}{{{{\sin }^2}\alpha }} - 1} = \sqrt {\frac{{{{\sin }^2}\alpha + {{\cos }^2}\alpha }}{{{{\sin }^2}\alpha {{\cos }^2}\alpha }} - 2} \\\,\,\,\,\,\,\,\,\,\,\,\, = \sqrt {{{\left( {\frac{1}{{\sin \alpha \cos \alpha }}} \right)}^2} - 2} = \sqrt {{{\left( { - \frac{9}{4}} \right)}^2} - 2} = \frac{7}{4}.\end{array}\) Chọn D. Câu hỏi 26 : Cho biết \(\cos \alpha = - \frac{2}{3}.\) Giá trị của biểu thức \(P = \frac{{\cot \alpha + 3\tan \alpha }}{{2\cot \alpha + \tan \alpha }}\) bằng bao nhiêu?
Đáp án: B Phương pháp giải: Áp dụng các công thức: \(\tan \alpha = \frac{{\sin \alpha }}{{\cos \alpha }};\,\,\,\cot \alpha = \frac{{\cos \alpha }}{{\sin \alpha }};\,\,\,{\sin ^2}\alpha + {\cos ^2}\alpha = 1.\) Lời giải chi tiết: Ta có: \({\sin ^2}\alpha + c{\rm{o}}{{\rm{s}}^2}\alpha = 1 \Leftrightarrow {\sin ^2}\alpha = 1 - c{\rm{o}}{{\rm{s}}^2}\alpha = 1 - \frac{4}{9} = \frac{5}{9}\) \( \Rightarrow P = \frac{{\frac{{{\rm{cos}}\alpha }}{{\sin \alpha }} + 3\frac{{\sin \alpha }}{{\cos \alpha }}}}{{2\frac{{\cos \alpha }}{{\sin \alpha }} + \frac{{\sin \alpha }}{{\cos \alpha }}}} = \frac{{{{\cos }^2}\alpha + 3{{\sin }^2}\alpha }}{{2{{\cos }^2}\alpha + {{\sin }^2}\alpha }} = \frac{{{{\left( { - \frac{2}{3}} \right)}^2} + 3.\frac{5}{9}}}{{2.{{\left( { - \frac{2}{3}} \right)}^2} + \frac{5}{9}}} = \frac{{19}}{{13}}.\) Chọn B Câu hỏi 27 : Cho tam giác \(ABC\). Tính giá trị của biểu thức: \(S = \frac{{{{\sin }^3}\frac{{\angle B}}{2}}}{{{\rm{cos}}\left( {\frac{{\angle A + \angle C}}{2}} \right)}} + \frac{{{\rm{co}}{{\rm{s}}^3}\frac{{\angle B}}{2}}}{{\sin \left( {\frac{{\angle A + \angle C}}{2}} \right)}} - \frac{{\cos \left( {\angle A + \angle C} \right)}}{{\sin \angle B}}.\tan \angle B\)
Đáp án: D Phương pháp giải: Áp dụng các công thức sau: \(\left\{ \begin{array}{l}{\sin ^2}\alpha + c{\rm{o}}{{\rm{s}}^2}\alpha = 1\\\tan \alpha .\cot \alpha = 1 \Rightarrow \tan \alpha .\frac{{\cos \alpha }}{{\sin \alpha }} = 1\\\sin \left( {{{90}^0} - \alpha } \right) = c{\rm{os}}\alpha \\\cos \left( {{{180}^0} - \alpha } \right) = - c{\rm{os}}\alpha \end{array} \right..\) Lời giải chi tiết: Ta có: \(\angle A + \angle B + \angle C = {180^o} \Rightarrow \angle A + \angle C = {180^o} - \angle B\) Lại có: \(\sin \left( {\frac{{{{180}^o} - \angle B}}{2}} \right) = \cos \frac{{\angle B}}{2};\,\,\,\,\cos \left( {\frac{{{{180}^o} - \angle B}}{2}} \right) = \sin \frac{{\angle B}}{2}.\) \(\begin{array}{l} \Rightarrow S = \frac{{{{\sin }^3}\frac{{\angle B}}{2}}}{{\cos \left( {\frac{{\angle A + \angle C}}{2}} \right)}} + \frac{{{{\cos }^3}\frac{{\angle B}}{2}}}{{\sin \left( {\frac{{\angle A + \angle C}}{2}} \right)}} - \frac{{\cos \left( {\angle A + \angle C} \right)}}{{\sin \angle B}}.\tan \angle B\\\,\,\,\,\,\,\,\,\,\,\, = \frac{{{{\sin }^3}\frac{{\angle B}}{2}}}{{\cos \left( {\frac{{{{180}^o} - \angle B}}{2}} \right)}} + \frac{{{{\cos }^3}\frac{{\angle B}}{2}}}{{\sin \left( {\frac{{{{180}^o} - \angle B}}{2}} \right)}} - \frac{{\cos \left( {{{180}^o} - \angle B} \right)}}{{\sin \angle B}}.\tan \angle B\\\,\,\,\,\,\,\,\,\, = \frac{{{{\sin }^3}\frac{{\angle B}}{2}}}{{\sin \frac{{\angle B}}{2}}} + \frac{{{{\cos }^3}\frac{{\angle B}}{2}}}{{\cos \frac{{\angle B}}{2}}} - \frac{{ - \cos \angle B}}{{\sin \angle B}}.\tan \angle B\\\,\,\,\,\,\,\,\,\, = {\sin ^2}\frac{{\angle B}}{2} + {\cos ^2}\frac{{\angle B}}{2} + \cot \angle B.\tan \angle B = 1 + 1 = 2.\end{array}\) Chọn D Câu hỏi 28 : Cho tam giác \(ABC\) và ba số dương \(x,y,z\) thay đổi có tổng bình phương \({x^2} + {y^2} + {z^2} = {k^2},k \in \mathbb{R}.\) Giá trị lớn nhất của \(P = xy\cos \angle C + yz\cos \angle A + zx\cos \angle B\) ?
Đáp án: A Phương pháp giải: Với 3 vecto \(\overrightarrow a ,\,\,\overrightarrow b ,\,\,\overrightarrow c :\,\,{\left( {\overrightarrow a + \overrightarrow b + \overrightarrow c } \right)^2} \ge 0.\) \(\cos \left( {{{180}^0} - \alpha } \right) = - \cos \alpha .\) Lời giải chi tiết: Đặt 3 vecto \(\overrightarrow {BX} ,\overrightarrow {CY} ,\overrightarrow {AZ} \) tương ứng là \(\overrightarrow x ,\,\,\overrightarrow y ,\,\,\overrightarrow z .\) Ta có: \(\begin{array}{l}{\left( {\overrightarrow x + \overrightarrow y + \overrightarrow z } \right)^2} \ge 0 \Leftrightarrow {x^2} + {y^2} + {z^2} + 2\overrightarrow x \overrightarrow y + 2\overrightarrow y \overrightarrow z + 2\overrightarrow z \overrightarrow x \ge 0\\ \Leftrightarrow {k^2} + 2xy\cos \left( {{{180}^o} - \angle C} \right) + 2yz\cos \left( {{{180}^o} - \angle A} \right) + 2xz\cos \left( {{{180}^o} - \angle B} \right) \ge 0\\ \Leftrightarrow {k^2} - 2xy\cos \angle C - 2yz\cos \angle A - 2xz\cos \angle B \ge 0\\ \Leftrightarrow xy\cos \angle C + yz\cos \angle A + xz\cos \angle B \le \frac{{{k^2}}}{2}\end{array}\) Vậy \({\rm{Max }}P{\rm{ = }}\frac{{{k^2}}}{2}\) Chọn A Câu hỏi 29 : Cho tam giác \(ABC.\) Tính \(P = \sin A.\cos \left( {B + C} \right) + \cos A.\sin \left( {B + C} \right)?\)
Đáp án: A Phương pháp giải: Nếu \(\alpha + \beta = {180^o}\) thì \(\sin \alpha = \sin \beta ;{\rm{ cos}}\alpha = - \cos \beta .\) Lời giải chi tiết: Giả sử \(\angle A = \alpha ;\,\,\,\angle B + \angle C = \beta \) \( \Rightarrow P = \sin A.\cos \left( {B + C} \right) + \cos A.\sin \left( {B + C} \right) = \sin \alpha \cos \beta - \cos \alpha \sin \beta .\) Trong tam giác \(ABC,\,\,\angle A + \angle B + \angle C = {180^o} \Rightarrow \alpha + \beta = {180^o}\) \( \Rightarrow \sin \alpha = \sin \beta ;{\rm{ cos}}\alpha = - \cos \beta .\) Vậy \(P = \sin \alpha \cos \beta + \cos \alpha \sin \beta = - \sin \alpha \cos \alpha + \cos \alpha \sin \alpha = 0.\) Chọn A. Câu hỏi 30 : Cho biết \(\cos \alpha + \sin \alpha = \frac{1}{3}.\) Giá trị của \(P = \sqrt {{{\tan }^2}\alpha + {{\cot }^2}\alpha } \) bằng bao nhiêu?
Đáp án: D Phương pháp giải: Áp dụng các công thức: \(\left\{ \begin{array}{l}1 + {\tan ^2}\alpha = \frac{1}{{{\rm{co}}{{\rm{s}}^2}\alpha }};\,\,\,\,1 + {\cot ^2}\alpha = \frac{1}{{{{\sin }^2}\alpha }}\\{\left( {\sin \alpha + \cos \alpha } \right)^2} = 1 + 2\sin \alpha \cos \alpha \end{array} \right..\) Lời giải chi tiết: Ta có: \(\cos \alpha + \sin \alpha = \frac{1}{3} \Rightarrow {\left( {\cos \alpha + \sin \alpha } \right)^2} = \frac{1}{9} \Leftrightarrow 1 + 2\sin \alpha \cos \alpha = \frac{1}{9} \Leftrightarrow \sin \alpha \cos \alpha = - \frac{4}{9}.\) \(\begin{array}{l} \Rightarrow P = \sqrt {{{\tan }^2}\alpha + {{\cot }^2}\alpha } = \sqrt {\frac{1}{{{{\cos }^2}\alpha }} - 1 + \frac{1}{{{{\sin }^2}\alpha }} - 1} = \sqrt {\frac{{{{\sin }^2}\alpha + {{\cos }^2}\alpha }}{{{{\sin }^2}\alpha {{\cos }^2}\alpha }} - 2} \\\,\,\,\,\,\,\,\,\,\,\,\, = \sqrt {{{\left( {\frac{1}{{\sin \alpha \cos \alpha }}} \right)}^2} - 2} = \sqrt {{{\left( { - \frac{9}{4}} \right)}^2} - 2} = \frac{7}{4}.\end{array}\) Chọn D. Quảng cáo
|