Phương pháp giải:

Tập hợp có n phần tử thì có \({2^n}\) tập hợp con.

Lời giải chi tiết:

Tập hợp A có 2 phần tử nên có \({2^2} = 4\) tập con.

Đáp án A.

Phương pháp giải:

Viết tập hợp A dưới dạng liệt kê các phần tử và đếm số phần tử của A.

Lời giải chi tiết:

\(A = \left\{ {x \in \mathbb{Z}; - 3 < x \le 4} \right\}\) \( \Rightarrow A = \left\{ { - 2; - 1;0;1;2;3;4} \right\}\).

Vậy tập hợp A có 7 phần tử.

Đáp án B.

Phương pháp giải:

Liệt kê các phần tử của tập hợp.

Lời giải chi tiết:

\(S = \left\{ {\left. {q \in \mathbb{Q}} \right|25{q^4} - 9{q^2} = 0} \right\}\).

\(25{q^4} - 9{q^2} = 0 \Leftrightarrow {q^2}\left( {25{q^2} - 9} \right) = 0\)\( \Leftrightarrow \left[ \begin{array}{l}{q^2} = 0\\25{q^2} - 9 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}q = 0\\q = \frac{3}{5}\\q = \frac{{ - 3}}{5}\end{array} \right..\)

Vậy \(S\) có 3 phần tử.

Chọn D.

Phương pháp giải:

Nhận xét tính đúng sai của mỗi đáp án.

Lời giải chi tiết:

Đáp án A: \(\left\{ 1 \right\} \subset \left[ {1;\frac{5}{2}} \right]\) đúng.

Ngoài ra các đáp án B, C, D đều sai.

Chọn A.

Phương pháp giải:

Viết tập hợp bằng cách liệt kê các phần tử.

Lời giải chi tiết:

Ta có: \(A = \left\{ {\left. {x \in \mathbb{N}} \right|x \le 5} \right\} \Rightarrow A = \left\{ {0;\,\,1;\,\,2;\,\,3;\,\,4;\,\,5} \right\}.\)

Chọn C.

Phương pháp giải:

Số tập con của tập hợp chứa \(n\) phần tử bằng \({2^n}.\)

Lời giải chi tiết:

Số tập con của tập hợp \(A\) là \({2^3} = 8.\)

Chọn B.

Phương pháp giải:

Liệt kê các phần tử trong tập hợp.

Lời giải chi tiết:

+) Đáp án A: \( - {x^2} + 5x - 2 = 0 \Leftrightarrow \left[ \begin{array}{l}x = \frac{{5 + \sqrt {17} }}{2}\\x = \frac{{5 - \sqrt {17} }}{2}\end{array} \right..\)

\( \Rightarrow \) loại đáp án A.

+) Đáp án B: \(\left| x \right| < 1 \Rightarrow  - 1 < x < 1.\)

\( \Rightarrow \) loại đáp án B.

+) Đáp án C: \({x^2} - 4x = 0 \Leftrightarrow x\left( {x - 4} \right) = 0 \Leftrightarrow \left[ \begin{array}{l}x = 0\\x = 4\end{array} \right.\)

\( \Rightarrow \) loại đáp án C.

+) Đáp án D: \({x^2} - 2x - 3 = 0 \Leftrightarrow \left[ \begin{array}{l}x =  - 1\,\, \notin \left( { - \infty ;\, - 1} \right)\\x = 3\,\,\, \notin \left( { - \infty ;\,\, - 1} \right)\end{array} \right.\)

\( \Rightarrow \left\{ {\left. {x \in \left( { - \infty ; - 1} \right)} \right|{x^2} - 2x - 3 = 0} \right\} = \emptyset .\)

Chọn D.

Phương pháp giải:

Liệt kê các tập con của \(X.\)

Lời giải chi tiết:

Các tập con của tập hợp \(X\) là: \(\emptyset ;\,\,\,\left\{ 1 \right\};\,\,\left\{ 2 \right\};\,\,\left\{ 3 \right\};\,\,\left\{ 4 \right\} ;\,\,\left\{ {1;\,\,2} \right\};\,\,\left\{ {1;\,\,3} \right\};\,\,\left\{ {1;\,\,4} \right\};\,\,\,\left\{ {2;\,\,3} \right\};\,\,\,\left\{ {2;\,\,4} \right\};\,\,\,\left\{ {3;\,\,4} \right\};\)

\(\left\{ {1;\,\,2;\,\,3} \right\};\,\,\left\{ {1;\,\,2;\,\,4} \right\};\,\,\left\{ {1;\,\,3;\,\,4} \right\};\,\,\,\left\{ {2;\,\,3;\,\,4} \right\};\,\,\,\left\{ {1;\,\,2;\,\,3;\,\,4} \right\}.\)

\(X\) có \(16\) tập con là khẳng định đúng

Chọn  A.

Phương pháp giải:

Giải tìm tập \(A\)  để tìm tập con của nó.

Lời giải chi tiết:

Ta có \(\sqrt x  \ge 0\,\,\forall x \ge 0 \Rightarrow 0 < \frac{{14}}{{3\sqrt x  + 6}} \le \frac{{14}}{6}\)

Mặt khác \(\frac{{14}}{{3\sqrt x  + 6}} \in \mathbb{Z} \Rightarrow \left[ \begin{array}{l}\frac{{14}}{{3\sqrt x  + 6}} = 1\\\frac{{14}}{{3\sqrt x  + 6}} = 2\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}3\sqrt x  + 6 = 14\\3\sqrt x  + 6 = 7\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}\sqrt x  = \frac{8}{3}\\\sqrt x  = \frac{1}{3}\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = \frac{{64}}{9}\,\,\,\left( {tm} \right)\\x = \frac{1}{9}\,\,\,\left( {tm} \right)\end{array} \right.\)

Vậy  \(A = \left\{ {\frac{1}{9};\frac{{64}}{9}} \right\}.\)

\( \Rightarrow \) Tất cả các tập con của tập hợp \(A\) là:  \(\emptyset ,\,\,\left\{ {\frac{1}{9}} \right\},\,\,\left\{ {\frac{{64}}{9}} \right\},\,\,\left\{ {\frac{1}{9};\frac{{64}}{9}} \right\}\).

Chọn D.

Phương pháp giải:

Tìm các tính chất đặc trưng của các phần tử của mỗi tập hợp.

Lời giải chi tiết:

Ta có các tập hợp \(A,B,C\) được viết dưới dạng nêu các tính chất đặc trưng là

\(A = \left\{ {\left. {x \in \mathbb{Z}} \right|\,\,\left| x \right| \le 4} \right\},\) \(B = \{ \left. {x \in \mathbb{N}} \right|\,x\) là số lẻ nhỏ hơn \(10\} \)  và  \(C = \{ {n^2}|\,\,\,n\) là số tự nhiên nhỏ hơn \(6\} .\) 

Chọn D.

Phương pháp giải:

\( \subset \) là ký hiệu cho mối quan hệ giữa 2 tập hợp, là kí hiệu tập hợp con.

\( \in \) là ký hiệu cho mối quan hệ giữa phần tử và tập hợp.

Lời giải chi tiết:

\(A \in A\) là mệnh đề sai, viết đúng là: \(A \subset A.\)

Chọn  A.

Phương pháp giải:

\( \subset \) là ký hiệu cho mối quan hệ giữa 2 tập hợp, là kí hiệu tập hợp con.

\( \in \) là ký hiệu cho mối quan hệ giữa phần tử và tập hợp.

Lời giải chi tiết:

Cách viết \(\left\{ a \right\} \subset \left[ {a;b} \right]\) là đúng.

Chọn  B.

Phương pháp giải:

Viết tập \(A\) dưới dạng chỉ ra tính chất đặc trưng của các phần tử.

Viết tập \(B\) dưới dạng liệt kê các phần tử.

Lời giải chi tiết:

Ta có \(A = \left\{ { - 1;\,\,1;\,\,5;\,\,8} \right\} \Rightarrow x \in \left\{ { - 1;\,\,1;\,\,5;\,\,8} \right\}\) là tập nghiệm của phương trình: \(\left( {x + 1} \right)\left( {x - 1} \right)\left( {x - 5} \right)\left( {x - 8} \right) = 0.\)

\( \Rightarrow A = \left\{ {x \in \mathbb{R}\left| {\left( {x + 1} \right)\left( {x - 1} \right)\left( {x - 5} \right)\left( {x - 8} \right) = 0} \right.} \right\}.\)

\(B = \) “Gồm các ước số nguyên dương của 16”
Mà \(U\left( {16} \right) = \left\{ { \pm 1;\,\, \pm 2;\, \pm 4;\, \pm 8;\, \pm 16} \right\} \Rightarrow B = \left\{ {1;\,\,2;{\rm{ }}4;\,\,8;{\rm{ }}16} \right\}.\) 

Chọn A.

Phương pháp giải:

Giải nghĩa và giải tập hợp.

Lời giải chi tiết:

Ta có \(\frac{{{x^2} + 2}}{x} = x + \frac{2}{x} \in \mathbb{Z}\) với \(x \in \mathbb{Z} \Leftrightarrow \frac{2}{x} \in \mathbb{Z} \Leftrightarrow 2\,\, \vdots \,\,x \Leftrightarrow x \in U\left( 2 \right) \Leftrightarrow x \in \left\{ { - 2; - 1;\,\,1;\,\,2} \right\}.\)

Vậy  \(A = \left\{ { - 2; - 1;1;2} \right\}.\)

Chọn  C.

Phương pháp giải:

Liệt kê các phần tử của A.

Lời giải chi tiết:

Ta có: \(x \le 5,\;\;x \in N \Rightarrow x \in \left\{ {0;\;1;\;2;\;3;\;4;\;5} \right\}.\)

\( \Rightarrow A = \left\{ {x + 1/x \in \mathbb{N},x \le 5} \right\} = \left\{ {x + 1/x \in \left\{ {0;\;1;\;2;\;3;\;4;\;5} \right\}} \right\} = \left\{ {1;\;2;\;3;\;4;\;5;\;6} \right\}\)

Chọn D.

Phương pháp giải:

\(A \cap B\) là tập gồm những phần tử thuộc cả A và B

Lời giải chi tiết:

Ta có: \(A\) là tập hợp các số tự nhiên lẻ nhỏ hơn \(14 \Rightarrow A = \left\{ {1;\;3;\;5;\;7;\;9;\;11;\;13} \right\}\,.\)

\(B\) là tập hợp các số nguyên tố nhỏ hơn \(10 \Rightarrow B = \left\{ {2;\;3;\;5;\;7} \right\}.\)

\(\, \Rightarrow A \cap B = \left\{ {3;\;5;\;7} \right\}.\)

Chọn D.

Phương pháp giải:

Liệt kê phần tử của tập hợp A.

Lời giải chi tiết:

\(A = \left\{ {x \in \mathbb{Z}| - 3 < x < 2} \right\} \Rightarrow A = \left\{ { - 2; - 1;\;0;\;1} \right\}.\)

Chọn C.

Phương pháp giải:

Liệt kê các phần tử của tập hợp.

Lời giải chi tiết:

\(A = \left\{ {x \in \mathbb{Z}\left| {1 < x \le 2} \right.} \right\} \Rightarrow A = \left\{ 2 \right\}\)

Chọn D.

Phương pháp giải:

Phủ định của một mệnh đề A, là một mệnh đề, kí hiệu là \(\overline A \). Hai mệnh đề A và \(\overline A \) có những khẳng định trái ngược nhau.

Nếu A đúng thì \(\overline A \) sai.

Nếu A sai thì \(\overline A \) đúng.

Lời giải chi tiết:

Mệnh đề phủ định của mệnh đề bài cho là: \(\overline P :\) “\(\exists x \in \mathbb{R}|{x^2} + x + 1 \le 0\)”

Chọn C.

Phương pháp giải:

Liệt kê các phần tử.

Lời giải chi tiết:

\(M = \left\{ {x \in \left. {{N^*}} \right|x < 4} \right\} = \left\{ {1;\;2;\;3} \right\}\)

Chọn D.

Phương pháp giải:

Liệt kê các phần tử của tập hợp.

Lời giải chi tiết:

\(A = \left\{ {x \in N\left| {x < 3} \right.} \right\} = \left\{ {0;\;1;\;2} \right\}.\)

Chọn A.

Phương pháp giải:

Tập rỗng là tập hợp không chứa phần tử nào.

Lời giải chi tiết:

+) Đáp án A : \(\left| x \right| < 1 \Leftrightarrow  - 1 < x < 1\)

Mà \(x \in Z \Rightarrow x = 0 \Rightarrow \) đáp án A sai.

+) Đáp án B : \(6{x^2} - 7x + 1 = 0 \Leftrightarrow \left( {x - 1} \right)\left( {6x - 1} \right) = 0 \Leftrightarrow \left[ \begin{array}{l}x = 1\; \in Z\\x = \frac{1}{6} \notin Z\end{array} \right. \Rightarrow \) đáp án B sai.

+) Đáp án C :  \({x^2} - 4x + 2 = 0 \Leftrightarrow \left[ \begin{array}{l}x = 2 + \sqrt 2 \,\,\, \notin Q\\x = 2 - \sqrt 2 \,\,\, \notin Q\end{array} \right. \Rightarrow \) đáp án C đúng.

+) Đáp án D : \({x^2} - 4x + 3 = 0 \Leftrightarrow \left( {x - 1} \right)\left( {x - 3} \right) = 0 \Leftrightarrow \left[ \begin{array}{l}x - 1 = 0\\x - 3 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 1 \in R\\x = 3 \in Z\end{array} \right. \Rightarrow \)đáp án D sai.

Vậy tập \(\left\{ {x \in Q;\;{x^2} - 4x + 2 = 0} \right\}\) là tập rỗng.

Chọn C.

Phương pháp giải:

Tập hợp rỗng là tập hợp không có phần tử nào.

Lời giải chi tiết:

Phương trình \({x^2} + x - 1 = 0 \Leftrightarrow x = \dfrac{{ - 1 \pm \sqrt 5 }}{2} \notin Z \Rightarrow \) Tập hợp \(\left\{ {x \in Z\left| {{x^2} + x - 1 = 0} \right.} \right\} = \emptyset \).

Chọn C.

Phương pháp giải:

\(B \subset A \Leftrightarrow \forall x \in B \Rightarrow x \in A\)

Lời giải chi tiết:

Các tập con của A là \(\emptyset ;\,\,\left\{ 1 \right\};\,\,\left\{ 2 \right\};\,\,\left\{ 3 \right\};\,\,\left\{ {1;2} \right\};\,\,\left\{ {1;3} \right\};\,\,\left\{ {2;3} \right\};\,\,A\).

Chọn C.

Phương pháp giải:

Giải các phương trình, tìm \(A,B,C\) từ đó tìm \(A \cup C\) để tìm \(\left( {A \cup C} \right)\backslash B.\)

Lời giải chi tiết:

\( \bullet \) Ta có: \(\left( {{x^2} + 7x + 6} \right)\left( {{x^2} - 4} \right) = 0 \Leftrightarrow \left[ \begin{array}{l}{x^2} + 7x + 6 = 0\\{x^2} - 4 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x =  - 1\\x =  - 6\\x =  - 2\\x = 2\end{array} \right..\)

 Vậy \(A = \left\{ { - 6; - 2; - 1;2} \right\}.\)

\( \bullet \) Ta có: \(\left\{ \begin{array}{l}x \in \mathbb{N}\\2x \le 8\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x \in \mathbb{N}\\x \le 4\end{array} \right. \Leftrightarrow x \in \left\{ {0;\,\,1;\,\,2;\,\,3;\,\,4} \right\}.\)

Vậy \(B = \left\{ {0;\,\,1;\,\,2;\,\,3;\,\,4} \right\}.\)

\( \bullet \) Ta có: \(\left\{ \begin{array}{l}x \in \mathbb{Z}\\ - 2 \le x \le 4\end{array} \right.\, \Leftrightarrow x \in \left\{ { - 2; - 1;\,\,0;\,\,1;\,\,2;\,\,3 ;\,\,4} \right\} \Rightarrow \left( {2x + 1} \right) \in \left\{ { - 3; - 1;\,1;\,3;\,\,5;\,\,7;\,\,9} \right\}.\)

\( \Rightarrow C = \left\{ { - 3; - 1;\,1;\,3;\,5;\,7;\,9} \right\}\)

Ta có: \(A \cup C = \left\{ { - 6; - 3; - 2; - 1;1;2;3;5;7;9} \right\}\)     

\( \Rightarrow \left( {A \cup C} \right)\backslash B = \left\{ { - 6; - 3; - 2; - 1;\,5;\,7;\,9} \right\}.\)

Chọn C.

Phương pháp giải:

\(A \subset B \Leftrightarrow \forall x:\,x \in A \Rightarrow x \in B\)

Lời giải chi tiết:

Các tập \(X\) thỏa mãn yêu cầu đề bài là:

\(\left\{ {1;2} \right\}\,\,,\,\,\left\{ {1;2;3} \right\},\,\,\left\{ {1;2;4} \right\}\,\,,\,\,\left\{ {1;2;5} \right\}\,\,,\,\,\left\{ {1;2;3;4} \right\}\,\,,\,\,\left\{ {1;2;3;5} \right\}\,\,,\,\,\left\{ {1;2;4;5} \right\}\,\,,\,\,\left\{ {1;2;3;4;5} \right\}.\)

Vậy có \(8\) tập \(X\)  thỏa mãn yêu cầu đề bài.

Chọn  A.

Phương pháp giải:

Giải tìm \(A,B,E.\)  \(B\backslash A = C_B^{}A\)

Lời giải chi tiết:

Ta có: \(\left( {{x^2} - 9} \right)\left( {{x^2} - 5x - 6} \right) = 0 \Leftrightarrow \left[ \begin{array}{l}{x^2} - 9 = 0\\{x^2} - 5x - 6 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 3\\x =  - 3\\x =  - 1\\x = 6\end{array} \right..\)

Các số nguyên tố nhỏ hơn \(6\) là: \(2;\,\,3;\,\,5.\)

\( \Rightarrow E = \left\{ {\left. {x \in \mathbb{N}} \right|\,1 \le x < 7} \right\} = \left\{ {1;\,\,2;\,\,3;\,\,4;\,\,5;\,\,6} \right\};\,\,A = \left\{ {\left. {x \in \mathbb{N}} \right|\left( {{x^2} - 9} \right)\left( {{x^2} - 5x - 6} \right) = 0} \right\} = \left\{ {3;\,\,6} \right\}\)  và  \(B = \left\{ {2;\,\,3;\,\,5} \right\}.\)

\(\begin{array}{l} \Rightarrow {C_E}A = E\backslash A = \left\{ {1;\,2;\,4;\,5} \right\};{\rm{ }}{C_E}B = E\backslash B = \left\{ {1;\,4;\,6} \right\}\\ \Rightarrow A \cup B = \left\{ {2;\,3;\,5;\,6} \right\} \Rightarrow {C_E}(A \cup B) = E\backslash \left( {A \cup B} \right) = \left\{ {1;\,4} \right\}.\end{array}\)

 Chọn  D.

Phương pháp giải:

\(B \subset A \Leftrightarrow \forall x \in B \Rightarrow x \in A\)

Lời giải chi tiết:

Ta có: \(\emptyset  \subset A\); \(\left\{ {1;2;4} \right\} \subset A\); \(0 \in A\) đúng.

Chọn C.

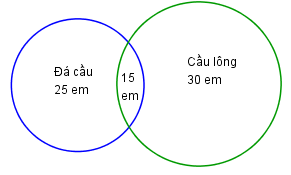
Phương pháp giải:

Liệt kê các phần tử của H.

Lời giải chi tiết:

\(H = \left\{ {x \in Z| - 2 \le x < 3} \right\} = \left\{ { - 2; - 1;0;1;2} \right\}\).

Chọn A.

Phương pháp giải:

Sử dụng biểu đồ Ven để giải bài toán.

Lời giải chi tiết:

Dựa vào biểu đồ ven ta suy ra số học sinh chỉ biết đá cầu là \(25 - 15 = 10\) (học sinh).

Số học sinh chỉ biết đánh cầu lông là \(30 - 15 = 15\) (học sinh).

Do đó ta có sĩ số học sinh của lớp  10A₁ là \(10 + 15 + 15 = 40\) (học sinh).

Chọn  B.