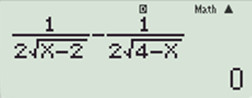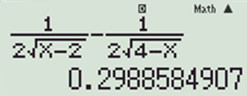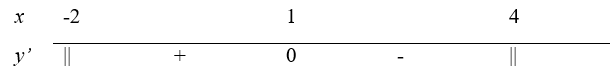30 bài tập trắc nghiệm sự đồng biến nghịch biến của hàm số mức độ thông hiểuLàm bàiQuảng cáo
Câu hỏi 1 : Hàm số \(y = \sqrt {4x - {x^2}} \) nghịch biến trên khoảng
Đáp án: A Phương pháp giải: Lời giải chi tiết: A Câu hỏi 2 : Cho hàm số\(y = {x^3} - \left( {m + 1} \right){x^2} - \left( {2{m^2} - 3m + 2} \right)x + 1\). Kết luận nào sau đây đúng?
Đáp án: C Phương pháp giải: Khảo sát sự biến thiên của hàm số để chọn đáp án đúng. Lời giải chi tiết: Ta có: \(y' = 3{x^2} - 2\left( {m + 1} \right)x - 2{m^2} + 3m - 2\) Ta có \(\begin{array}{l}\Delta ' = {\left( {m + 1} \right)^2} + 3\left( {2{m^2} - 3m + 2} \right) = 7{m^2} - 7m + 7 = 7\left( {{m^2} - m + 1} \right)\\\,\,\,\,\,\, = 7\left( {{{\left( {m - \dfrac{1}{2}} \right)}^2} + \dfrac{3}{4}} \right) > 0\,\,\,\forall m\end{array}\) Khi đó phương trình \(y' = 0\) có 2 nghiệm phân biệt. Suy ra hàm số không đơn điệu trên \(\mathbb{R}\). Chọn C. Câu hỏi 3 : Cho hàm số \(y = f\left( x \right) = \dfrac{{{x^2} + x + 2}}{{x - 1}}\). Khẳng định nào trong các khẳng định sau là sai?
Đáp án: A Phương pháp giải: - Tính \(y’\) và kết luận các khoảng đơn điệu của hàm số. Lời giải chi tiết: TXĐ: \(D=R\backslash \left\{ 1 \right\}\) \( \Rightarrow \) Đáp án D đúng. Có \(f'\left( x \right)=\dfrac{\left( 2x+1 \right)\left( x-1 \right)-{{x}^{2}}-x-2}{{{\left( x-1 \right)}^{2}}}=\dfrac{{{x}^{2}}-2x-3}{{{\left( x-1 \right)}^{2}}}\Rightarrow \) Đáp án B đúng. \(\Rightarrow f'\left( x \right)=0\Leftrightarrow {{x}^{2}}-2x-3=0\Leftrightarrow \left[ \begin{align} x=-1 \\x=3 \\\end{align} \right.\) Hàm số đồng biến trong khoảng \(\left( { - \infty ; - 1} \right)\) và \(\left( 3;+\infty \right)\) đáp án C đúng. hàm số nghịch biến trong khoảng \(\left( -1;1 \right)\) và \(\left( 1;3 \right)\) \(\Rightarrow \) đáp án A sai. Chọn A. Câu hỏi 4 : Hàm số \(y = - {x^5} + {x^3} - 1\) nghịch biến trên khoảng nào trong các khoảng sau?
Đáp án: A Phương pháp giải: - Tính \(y'\) và kết luận các khoảng đơn điệu của hàm số. Lời giải chi tiết: Ta có: \(y'=-5{{x}^{4}}+3{{x}^{2}}\). Hàm số nghịch biến thì \(y'\le 0\). Nhập hàm y’ vào máy tính để thử với các giá trị tương ứng trong từng khoảng đáp án. Thử với \(x=-1\) ta được \(y' = - 2 < 0\) \( \Rightarrow \) hàm số nghịch biến.
Thử với \(x=1\) ta được \(y'=-2<0\) \(\Rightarrow \) hàm số nghịch biến.
\(\Rightarrow \) Loại đáp án B và D. Thử với \(x=\frac{7}{10}\) ta được \(y'=\frac{539}{2000}>0\) \( \Rightarrow \) hàm số đồng biến
\(\Rightarrow \) loại đáp án C. Chọn A. Câu hỏi 5 : Hàm số \(y = \dfrac{{{x^3}}}{3} - \dfrac{{m{x^2}}}{2} - 2x + 1\) đồng biến trên tập xác định khi:
Đáp án: D Phương pháp giải: Sử dụng chức năng MODE 7 để xử lý bài toán. Lời giải chi tiết: Cách 1: Ta có \(y' = {x^2} - mx - 2\). Hàm số đồng biến trên tập xác định \( \Leftrightarrow y' \ge 0\,\forall x\). Ta sử dụng máy tính để thử đáp án. +) Trước hết ta thử với \(m = 2\sqrt 2 \). Khi đó: \(y'={{x}^{2}}-2\sqrt{2}x-2\). Nhập hàm số trên vào máy tính và thử với giá trị \(x=0\) ta được \(y'=-2<0\). Loại đáp án C. +) Thử với giá trị \(m = 0\). Khi đó \(y'={{x}^{2}}-2\). Với \(x=0\) ta được \(y' = - 2 < 0\) Loại đáp án B. +) Thử với \(m=-3\). Khi đó \(y'={{x}^{2}}+3x-2\). Với \(x=0\) ta được \(y'=-2<0\). \( \Rightarrow \) Loại đáp án A. Cách 2: TXĐ: D = R. Ta có: \(y' = {x^2} - mx - 2\) Để hàm số đồng biến trên tập xác định thì \(\begin{array}{l} Vậy không có giá trị nào của m thỏa mãn yêu cầu bài toán. Chọn đáp án D. Câu hỏi 6 : Cho hàm số \(f\left( x \right)\) có \(f'\left( x \right) \le 0,\,\forall x \in R\) và \(f'\left( x \right) = 0\) chỉ tại một số hữu hạn điểm thuộc R. Hỏi khẳng định nào sau đây là khẳng định đúng?
Đáp án: C Phương pháp giải: - Sử dụng định nghĩa đồng biến, nghịch biến. Lời giải chi tiết: Theo đề bài ta suy ra hàm số \(f\left( x \right)\) là hàm nghịch biến trên R. Phân tích từng đáp án ta có: +) Đáp án A: Với \({x_1} < {x_2} < {x_3} \Rightarrow f\left( {{x_1}} \right) > f\left( {{x_2}} \right) > f\left( {{x_3}} \right) \Rightarrow \dfrac{{f\left( {{x_1}} \right) - f\left( {{x_2}} \right)}}{{f\left( {{x_2}} \right) - f\left( {{x_3}} \right)}} > 0\) loại A. +) Đáp án B: Với \({x_1} > {x_2} > {x_3} \Rightarrow f\left( {{x_1}} \right) < f\left( {{x_2}} \right) < f\left( {{x_3}} \right) \Rightarrow \dfrac{{f\left( {{x_1}} \right) - f\left( {{x_2}} \right)}}{{f\left( {{x_2}} \right) - f\left( {{x_3}} \right)}} > 0 \Rightarrow \) loại B. +) Đáp án C: Với \({x_1} \ne {x_2} \Rightarrow f\left( {{x_1}} \right) \ne f\left( {{x_2}} \right)\) và vì hàm số nghịch biến nên dấu của biểu thức \(\left( {{x_1} - {x_2}} \right)\) và \(\left[ {f\left( {{x_1}} \right) - f\left( {{x_2}} \right)} \right]\) ngược dấu \( \Rightarrow \dfrac{{f\left( {{x_1}} \right) - f\left( {{x_2}} \right)}}{{{x_1} - {x_2}}} < 0 \Rightarrow \) C đúng. Chọn C. Câu hỏi 7 : Cho hàm số \(y = {x^3} + 3{x^2} + 3x + 1\) có đồ thị (C). Tìm câu sai.
Đáp án: B Phương pháp giải: - Xét từng đáp án. - Hàm số \(y = f\left( x \right)\) đồng biến trên \(\left( a;b \right)\Leftrightarrow f'\left( x \right)\le 0\,\,\forall x\in \left( a;b \right)\). Lời giải chi tiết: Ta có: \(y'=3{{x}^{2}}+6x+3=3{{\left( x+1 \right)}^{2}}\ge 0\,\,\,\forall x\). hàm số đồng biến trên R. \( \Rightarrow \) Đáp án D đúng. Xét phương trình: \({{x}^{3}}+3{{x}^{2}}+3x+1=0\Leftrightarrow {{\left( x+1 \right)}^{3}}=0\Leftrightarrow x=-1\). \(\Rightarrow \) (C) chỉ cắt trục \(Ox\) tại một điểm duy nhất. \( \Rightarrow \) Đáp án A đúng. Ta có: \(y'=3{{x}^{2}}+6x+3\,\Rightarrow y''=6x+6\). Hoành độ của điểm uốn là nghiệm của phương trình \(y''=0\Leftrightarrow x=-1\). \(\Rightarrow \) Điểm uốn \(I\left( { - 1;0} \right)\) \(\Rightarrow \) phương trình tiếp tuyến của (C) tại I là: \(y=y'\left( -1 \right)\left( x+1 \right)=0\). \(\Rightarrow \) Đáp án C đúng. Vậy chọn B. Câu hỏi 8 : Cho hàm số \(y = \cos x + ax\). Với giá trị nào của a thì hàm số đồng biến trên R.
Đáp án: C Phương pháp giải: - Hàm số \(y = f\left( x \right)\) đồng biến trên \(\left( a;b \right)\Leftrightarrow f'\left( x \right)\ge 0\,\,\forall x\in \left( a;b \right)\). Lời giải chi tiết: Ta có: \(y'=-\sin x+a\) \(\Rightarrow \) Hàm số đồng biến với mọi x \( \Leftrightarrow y' \ge 0\) với mọi x \(\Leftrightarrow -\sin x+a\ge 0\) với mọi x \(\Leftrightarrow a\ge \sin x\) với mọi x \(\Leftrightarrow a\ge 1\) (vì \(\sin x \le 1\)) Chọn C. Câu hỏi 9 : Hàm số \(y=\dfrac{m}{3}{{x}^{3}}-\left( m-1 \right){{x}^{2}}+3\left( m-2 \right)x+\dfrac{1}{3}\) đồng biến trên \(\left( {2; + \infty } \right)\) thì m thuộc tập nào:
Đáp án: A Phương pháp giải: - Chọn m. - Sử dụng MTCT tính \(y'\left( {{x}_{0}} \right)\) với \({{x}_{0}}\) là điểm bất kì thuộc các đáp án. Lời giải chi tiết: Ta có: \(y' = m{x^2} - 2\left( {m - 1} \right)x + 3\left( {m - 2} \right)\). Hàm số đồng biến trên \(\left( {2; + \infty } \right)\) khi \(y' \ge 0\) trong \(\left( 2;+\infty \right)\). Ta thử từng đáp án để chọn đáp án đúng. +) Đáp án A: Với \(m = \dfrac{2}{3}\) ta có: \(y' = \dfrac{2}{3}{x^2} + \dfrac{2}{3}x - 4\) Ta nhập hàm y’ vào máy tính và thử giá trị \(x = 2\) ta được \(y' = 0\) nên đáp án A có thể đúng.
Để chắc chắn, ta thử với giá trị \(x = 3\) ta được \(y' = 4 > 0\) nên hàm số đồng biến.
Vậy đáp án A đúng. Chọn A. Câu hỏi 10 : Trong các hàm số sau, hàm số nào nghịch biến trên khoảng \(\left( { - 1; + \infty } \right)\).
Đáp án: D Phương pháp giải: Sử dụng MTCT tính \(y'\left( {{x}_{0}} \right)\) với \({{x}_{0}}\) là điểm bất kì thuộc các đáp án. Lời giải chi tiết: Sử dụng máy tính CASIO dùng chức năng Shift \(\dfrac{d}{{dx}}{\left. {\left( {} \right)} \right|_{x = ?}}\) ta tính đạo hàm từng đáp án nếu đáp án nào ra kết quả 1 số \( \le 0\) thì đáp án đó đúng, còn đáp án nào ra kết quả > 0 thì đáp án đó sai. Ta có: +) Đáp án A. Tại \(x = 6\) ta có :
+) Đáp án B: Ta sẽ thử với x = 1. Vì ĐKXĐ: \(x>0\).
+) Đáp án C: Ta có: Chọn D. Câu hỏi 11 : Hàm số \(y=\sqrt{x-2}+\sqrt{4-x}\) nghịch biến trên:
Đáp án: A Phương pháp giải: Sử dụng MTCT tính \(y'\left( {{x}_{0}} \right)\) với \({{x}_{0}}\) là điểm bất kì thuộc các đáp án. Lời giải chi tiết: TXĐ: \(D = \left[ {2;4} \right]\) Ta có: \(y'=\dfrac{1}{2\sqrt{x-2}}-\dfrac{1}{2\sqrt{4-x}}\). Nhập hàm y’ vào máy tính Casio sau đó ta sử dụng chức năng CALC từng đáp án nếu kết quả đáp án nào ra y’ ≤ 0 thì là đúng. Ta sẽ chọn đáp án đó +) Với đáp án A ta thử giá trị \(x=3\)
ta thấy \(y' = 0\) nên đáp án A có thể là đáp án đúng. +) Ta loại được đáp án B và C +) Thử đáp án D CALC giá trị 2,5 ta được kết quả y’ > 0 như sau:
Nên ta loại đáp án D. Chọn A. Câu hỏi 12 : Tìm tất cả các giá trị thực của m để hàm số \(y=\frac{\cos x-1}{\cos x-m}\) đồng biến trên \(\left( 0;\frac{\pi }{2} \right).\)
Đáp án: B Phương pháp giải: Đặt ẩn phụ, tìm điều kiện của ẩn phụ, xét hàm. Lời giải chi tiết: Cách 1: Khi m = 1 ta có: y = 1 là hàm hằng nên m = 1 không thỏa mãn. Khi \(m\ne 1\). Đặt \(t=\cos x\). Vì \(x\in \left( 0;\frac{\pi }{2} \right)\) nên \(t\in \left( 0;1 \right)\). Xét hàm \(y = \frac{{t - 1}}{{t - m}}\,\,\,\,\left( {TXD:\,\,D = R\backslash \left\{ m \right\}} \right)\) có \(y'=\frac{t-m-t+1}{{{\left( t-m \right)}^{2}}}=\frac{1-m}{{{\left( t-m \right)}^{2}}}\). Để hàm số đã cho đồng biến trên \(\left( 0;\frac{\pi }{2} \right)\) thì hàm số \(y=\frac{t-1}{t-m}\) nghịch biến trên \(\left( 0;1 \right)\) \( \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{1 - m < 0}\\{m \notin \left( {0;1} \right)}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{m > 1}\\{\left[ {\begin{array}{*{20}{c}}{m \le 0}\\{m \ge 1}\end{array}} \right.}\end{array}} \right.\Leftrightarrow m > 1\) Cách 2: Khi m = 1 ta có: y = 1 là hàm hằng nên m = 1 không thỏa mãn. Khi \(m \ne 1\). Ta có \(y' = \frac{{ - \sin x\left( {\cos x - m} \right) + \left( {\cos x - 1} \right)\sin x}}{{{{\left( {\cos x - m} \right)}^2}}} = \frac{{m\sin x - \sin x}}{{{{\left( {\cos x - m} \right)}^2}}}\) Để hàm số đồng biến trên \(\left( {0;\frac{\pi }{2}} \right) \Rightarrow \left\{ \begin{array}{l}y' > 0\,\,\forall x \in \left( {0;\frac{\pi }{2}} \right)\\m \ne \cos x\,\,\forall x \in \left( {0;\frac{\pi }{2}} \right)\end{array} \right.\) \( \Rightarrow \left\{ \begin{array}{l}\sin x\left( {m - 1} \right) > 0\,\,\forall x \in \left( {0;\frac{\pi }{2}} \right)\\m \notin \left( {0;1} \right)\end{array} \right.\) Do \(x \in \left( {0;\frac{\pi }{2}} \right) \Rightarrow \sin x > 0 \Rightarrow m - 1 > 0 \Leftrightarrow m > 1 \Leftrightarrow \left\{ \begin{array}{l}m > 1\\m \notin \left( {0;1} \right)\end{array} \right. \Rightarrow m > 1\) Chọn B. Chọn B.
Câu hỏi 13 : Tìm tất cả các giá trị thực của tham số \(m\) để hàm số \(y = mx - \sin x\) đồng biến trên \(\mathbb{R}.\)
Đáp án: C Phương pháp giải: Phương pháp giải. Sử dụng kết quả: hàm số \(y = f\left( x \right)\) đồng biến trên tập \(D\) nào đó khi và chỉ khi đạo hàm của hàm số trên tập \(D\) không âm, tức là \(f'\left( x \right) \ge 0,\,\,\forall x \in D.\) Áp dụng vào bài tập này ta đi tính đạo hàm \(y'.\) Sau đó cho \(y'\ge 0,\,\,\forall x\in \mathbb{R}\) để tìm giá trị của \(m\) Lời giải chi tiết: Lời giải chi tiết. Để hàm số đã cho đồng biến trên \(\mathbb{R}\) thì điều kiện cần và đủ là \(y'\ge 0\Leftrightarrow \left( mx-\sin x \right)'\ge 0\Leftrightarrow m-\cos x\ge 0\Leftrightarrow m\ge \cos x\,,\forall x\in \mathbb{R}.\) Do \(-1\le \cos x\le 1,\forall x\in \mathbb{R},\) nên ta có \(m\ge \cos x,\,\forall x\in \mathbb{R}\Leftrightarrow m\ge 1.\) Chọn đáp án C. Câu hỏi 14 : Tìm \(m\) để hàm số \(y={{x}^{3}}-3{{x}^{2}}+mx+2\) tăng trên khoảng \(\left( 1;+\infty \right).\)
Đáp án: A Phương pháp giải: Phương pháp. Dùng tính chất hàm số \(y=f\left( x \right)\) tăng hay đồng biến trên tập \(D\) khi \(y'=f'\left( x \right)\ge 0,\,\,\forall x\in D.\) Lời giải chi tiết:
Lời giải chi tiết. Ta có \(y'=3{{x}^{2}}-6x+m.\) Để hàm số đã cho tăng trên \(\left( 1;+\infty \right)\) thì \(y'>0,\,\forall x\in \left( 1;+\infty \right)\Leftrightarrow 3{{x}^{2}}-6x+m>0,\,\,\forall x\in \left( 1;+\infty \right).\) Xét hàm số \(f\left( x \right)=3{{x}^{2}}-6x\) trên \(\left( 1;+\infty \right).\) Ta có \(f\left( x \right)=3{{x}^{2}}-6x=3{{\left( x-1 \right)}^{2}}-3>-3,\,\,\forall x\in \left( 1;+\infty \right).\) Do đó nếu \(-3+m\ge 0\Leftrightarrow m\ge 3.\) thì ta có \(3{{x}^{2}}-6x+m>0,\,\,\forall x\in \left( 1;+\infty \right).\) Hay hàm số đã cho tăng trên \(\left( 1;+\infty \right).\) Chọn đáp án A. Câu hỏi 15 : Cho hàm số \(y=f(x)\) có đạo hàm trên \(\mathbb{R}\) và \(f'(x)>0,\,\,\forall x\in \left( 0;\,+\infty \right)\). Biết \(f(1)=2\). Khẳng định nào dưới đây có thể xảy ra?
Đáp án: C Phương pháp giải: Dựa vào tính đơn điệu của hàm số để loại trừ đáp án sai dựa vào tính đơn điệu của hàm số. Lời giải chi tiết: Vì \(f'(x)>0,\,\,\forall x\in \left( 0;\,+\infty \right)\) nên hàm số \(y=f(x)\)đồng biến trên khoảng \(\left( 0;\,+\infty \right)\) \(\Rightarrow \) Loại bỏ các đáp án: +) Đáp án A (do \(f(2)>f(1)=2\)), +) Đáp án B (do \(2017<2018\Rightarrow f(2017)<f(2018)\), +) Đáp án D (do \(f(3)>f(2)>f(1)=2\Rightarrow f(2)+f(3)>2+2\Leftrightarrow f(2)+f(3)>4\)). Như vậy, chỉ có khẳng định ở đáp án C là có thể xảy rA. Chọn C. Câu hỏi 16 : Tìm tập hợp \(S\) tất cả các giá trị của tham số thực \(m\) để hàm số \(y=\frac{{{x}^{3}}}{3}+m{{x}^{2}}+\left( 2m+3 \right)x+1\) đồng biến trên \(R\).
Đáp án: B Phương pháp giải: Hàm số bậc ba \(y=f\left( x \right)\) đồng biến trên \(R\Leftrightarrow y'\ge 0,\forall x\in R\). Và chỉ bằng 0 tại hữu hạn điểm. Lời giải chi tiết: Ta có \(y'={{x}^{2}}+2mx+2m+3\). Để hàm số đồng biến trên \(R\) thì \(y'\ge 0,\forall x\in R\Leftrightarrow \left\{ \begin{align} & a>0 \\ & \Delta '\le 0 \\\end{align} \right.\) \(\Leftrightarrow \left\{ \begin{align} & 1>0 \\ & {{m}^{2}}-\left( 2m+3 \right)\le 0 \\\end{align} \right.\Leftrightarrow {{m}^{2}}-2m-3\le 0\Leftrightarrow -1\le m\le 3\) Vậy \(m\in \left[ -1;3 \right]\). Chọn B. Câu hỏi 17 : Tìm tất cả các giái trị thực của tham số m để hàm số \(y=\frac{mx+2}{2x+m}\) nghịch biến trên từng khoảng xác định của nó?
Đáp án: B Phương pháp giải: Điều kiện để hàm số nghịch biến trên \(\left( a;b \right)\) là \(y'<0,\forall x\in \left( a;b \right)\). Lời giải chi tiết: Ta có \(y'=\frac{{{m}^{2}}-4}{{{\left( x+m \right)}^{2}}}\). Để hàm số đã cho nghịch biến thì \(y'<0\) \(\Leftrightarrow {{m}^{2}}-4<0\Rightarrow -2<m<2\) Đáp án B Câu hỏi 18 : Cho hàm số \(y=f(x)\) có đạo hàm \(f'\left( x \right)={{x}^{2}}+1,\forall x\in R\). Mệnh đề nào dưới đây đúng?
Đáp án: B Phương pháp giải: Hàm số \(y=f\left( x \right)\) có đạo hàm \(f'\left( x \right)>0,\forall x\in \left( a;b \right)\) thì nó đồng biến trên \(\left( a;b \right)\). Lời giải chi tiết: \(f'(x)={{x}^{2}}+1>0,\forall x\in R\) \(\Rightarrow f\left( x \right)\) là hàm số đồng biến trên R. Đáp án B Câu hỏi 19 : Cho hàm số \(y=f(x)\) xác định, liên tục và có đạo hàm trên đoạn \(\left[ a;b \right]\). Xét các khẳng định sau: 1.Hàm số f(x) đồng biến trên \((a;b)\) thì \(f'(x)>0,\forall x\in \left( a;b \right)\) 2.Giả sử \(f\left( a \right)>f\left( c \right)>f\left( b \right),\forall c\in \left( a,b \right)\) suy ra hàm số nghịch biến trên \(\left( a;b \right)\) 3. Giả sử phương trình \(f'(x)=0\) có nghiệm là \(x=m\) khi đó nếu hàm số \(f(x)\) đồng biến trên \(\left( m,b \right)\) thì hàm số f(x) nghịch biến trên \(\left( a,m \right).\) 4. Nếu \(f'(x)\ge 0,\forall x\in \left( a,b \right)\), thì hàm số đồng biến trên \(\left( a,b \right)\) Số khẳng định đúng trong các khẳng định trên là
Đáp án: A Phương pháp giải: Xét tính đúng sai của các đáp án dựa vào các kiến thức hàm số đồng biến, nghịch biến trên khoảng xác định. Lời giải chi tiết: *2 sai vì với \({{c}_{1}}<{{c}_{2}}\) bất kỳ nằm trong \(\left( a,b \right)\) ta chưa thể so sánh được \(f\left( {{c}_{1}} \right)\) và \(f\left( {{c}_{2}} \right)\). *3 sai. Vì \(y'\) bằng 0 tại điểm đó thì chưa chắc đã đổi dấu qua điểm đó. VD hàm số \(y={{x}^{3}}.\) *4 sai: Vì thiếu điều kiện \(f'\left( x \right)=0\) tại hữu hạn điểm.VD hàm số y = 1999 có \(y'=0\ge 0\) nhưng là hàm hằng. Đáp án A. Câu hỏi 20 : Tập hợp tất cả các giá trị của m để hàm số \(y=\frac{1}{3}{{x}^{3}}-\left( m-1 \right){{x}^{2}}+2\left( m-1 \right)x-2\) luôn tăng trên \(R\)
Đáp án: D Phương pháp giải: Tính \(y'\) và tìm điều kiện của \(m\) để \(y'>0,\forall x\in R\). Điều kiện để tam thức bậc hai \(a{{x}^{2}}+bx+c>0,\forall x\in R\) là \(\left\{ \begin{array}{l}a > 0\\\Delta \le 0\end{array} \right.\) Lời giải chi tiết: Xét hàm số: \(y=\frac{1}{3}{{x}^{3}}-\left( m-1 \right){{x}^{2}}+2\left( m-1 \right)x-2\) trên \(R\) Có \(y'\left( x \right)={{x}^{2}}-2\left( m-2 \right)x+2\left( m-1 \right).\) Hàm số đã cho tăng trên \(R\Leftrightarrow y'\left( x \right)>0,\forall x\in R\) \(\Leftrightarrow \Delta '={{\left( m-1 \right)}^{2}}-2\left( m-1 \right)\le 0\) vì \(a=1>0.\) \(\Leftrightarrow {{m}^{2}}-4m+3\le 0\) \(\Leftrightarrow 1\le m\le 3.\) Đáp án D. Câu hỏi 21 : Trong các hàm số sau, hàm số nào nghịch biến trên khoảng \(\left( 0;\sqrt{2} \right)\)
Đáp án: C Phương pháp giải: Xét các hàm số ở từng đáp án, tìm khoảng nghịch biến của chúng và đối chiếu điều kiện đề bài. Lời giải chi tiết: *TH1: Đáp án A: Hàm số: \(y=\frac{{{x}^{2}}+x-1}{x-1}\) xác định trên \(D=R\backslash \left\{ 1 \right\}\) nên loại A vì \(1\in \left( 0;\sqrt{2} \right)\) *TH2: Đáp án B: Xét hàm số: \(y=\frac{2x-5}{x+1}\) xác định trên \(R\backslash \left\{ -1 \right\}\) Có \(y'\left( x \right)=\frac{7}{{{\left( x+1 \right)}^{2}}},\forall x\in R\backslash \left\{ -1 \right\}\) \(\Rightarrow \) Hàm số \(y=\frac{2x-5}{x+1}\) đồng biến trên \(R\backslash \left\{ -1 \right\}\) (loại). *TH3: Đáp án C: Hàm số \(y=\frac{1}{2}{{x}^{4}}-2{{x}^{2}}+3\). liên tục trên \(\left( 0;\sqrt{2} \right).\) Có \(y'\left( x \right)=2{{x}^{3}}-6x<0,\forall x\in \left( 0;\sqrt{2} \right)\) \(\Rightarrow \) Hàm số: \(y=\frac{1}{2}{{x}^{4}}-2{{x}^{2}}+3\) nghịch biến trên \(\left( 0;\sqrt{2} \right).\) *TH4: Đáp án D: Hàm số: \(y=\frac{3}{2}{{x}^{3}}-4{{x}^{2}}+6x+9\) xác định trên \(R\) Có \(y'\left( x \right)=\frac{9}{2}{{x}^{2}}-8x+6=\frac{9}{2}{{\left( x-\frac{8}{9} \right)}^{2}}+\frac{22}{9}>0,\forall x\in R\) (loại). Vậy đáp án C thỏa mãn yêu cầu đề bài. Đáp án C. Câu hỏi 22 : Có tất cả bao nhiêu giá trị nguyên của \(m\) để hàm số \(y = \frac{{x + m}}{{mx + 4}}\) đồng biến trên từng khoảng xác định?
Đáp án: C Phương pháp giải: +) Hàm số \(y = \frac{{ax + b}}{{cx + d}}\) luôn đồng biến hoặc nghịch biến trên từng khoảng xác định của nó. +) Hàm số đồng biến \( \Leftrightarrow y' \ge 0\,\,\forall x \in D\) và chỉ bằng 0 tại hữu hạn điểm thuộc D, với D là tập xác định của hàm số. Lời giải chi tiết: Tập xác định: \(D = R\backslash \left\{ { - \frac{4}{m}} \right\};\,\,\,m \ne 0.\) Ta có: \(y' = \frac{{4 - {m^2}}}{{{{\left( {mx + 4} \right)}^2}}}.\) \( \Rightarrow \) Hàm số đồng biến trên D \( \Leftrightarrow 4 - {m^2} \ge 0 \Leftrightarrow {m^2} \le 4 \Leftrightarrow - 2 \le m \le 2.\) +) Với \(m = - 2\), hàm số có dạng: \(y = \frac{{x - 2}}{{ - 2x + 4}} = - \frac{1}{2}\) là hàm hằng \( \Rightarrow m = - 2\) không thỏa mãn. +) Với \(m = 2\), hàm số có dạng: \(y = \frac{{x + 2}}{{2x + 4}} = \frac{1}{2}\) là hàm hằng \( \Rightarrow m = 2\) không thỏa mãn. +) Với \(m = 0,\) hàm số có dạng: \(y = x\) đồng biến trên R. Vậy các giá trị nguyên của m thỏa mãn là: \(m \in \left\{ { - 1;0;\,\,1} \right\}.\) Chọn C. Câu hỏi 23 : Tìm tất cả các giá trị thực của tham số m để trên \(\left( -1;1 \right)\) , hàm số \(y=\frac{mx+6}{2x+m+1}\) nghịch biến.
Đáp án: D Phương pháp giải: Tìm m để hàm số \(y=\frac{ax+b}{cx+d}\) đồng biến, nghịch biến trên khoảng \(\left( \alpha ;\beta \right)\) - Bước 1: Tính \(y'\). - Bước 2: Nêu điều kiện để hàm số đồng biến, nghịch biến: + Hàm số đồng biến trên \(\left( \alpha ;\beta \right)\Leftrightarrow \left\{ \begin{align} & y'=f'\left( x \right)>0,\forall x\in \left( \alpha ;\beta \right) \\ & -\frac{d}{c}\notin \left( \alpha ;\beta \right) \\\end{align} \right.\) + Hàm số nghịch biến trên \(\left( \alpha ;\beta \right)\Leftrightarrow \left\{ \begin{align} & y'=f'\left( x \right)<0,\forall x\in \left( \alpha ;\beta \right) \\ & -\frac{d}{c}\notin \left( \alpha ;\beta \right) \\\end{align} \right.\) - Bước 3: Kết luận. Lời giải chi tiết: \(y=\frac{mx+6}{2x+m+1}\Rightarrow y'=\frac{m\left( m+1 \right)-6.2}{{{\left( 2x+m+1 \right)}^{2}}}=\frac{{{m}^{2}}+m-12}{{{\left( 2x+m+1 \right)}^{2}}}\) Hàm số nghịch biến trên \(\left( { - 1;1} \right) \Leftrightarrow \left\{ \begin{array}{l} Chọn D.
Câu hỏi 24 : Tìm giá trị của m để hàm số \(y=-\frac{1}{3}{{x}^{3}}-m{{x}^{2}}+\left( 2m-3 \right)x-m+2\) nghịch biến trên tập xác định.
Đáp án: B Phương pháp giải: Hàm số nghịch biến trên tập xác định \(\Leftrightarrow y'\le 0\) trên tập xác định và chỉ bằng 0 tại hữu hạn điểm. Lời giải chi tiết: Tập xác định: \(D=R.\) Ta có: \(y'=-{{x}^{2}}-2mx+2m-3\) \(\Rightarrow \) Hàm số nghịch biến trên tập xác định \(\Leftrightarrow y'\le 0\,\,\forall x\in R\Leftrightarrow -{{x}^{2}}-2mx+2m-3\le 0\,\,\forall \,\,x\in R\) \( \Leftrightarrow \left\{ \begin{array}{l}a < 0\\\Delta ' \le 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l} - 1 < 0\,\,\forall \,m\\{m^2} + 2m - 3 \le 0\end{array} \right. \Leftrightarrow - 3 \le m \le 1.\) +) Xét với \(m=-3\) ta có: \(y'=-{{x}^{2}}+6x-9=-{{\left( x-3 \right)}^{2}}\le 0\,\,\forall x\in R\Rightarrow m=-3\) thì hàm số nghịch biến trên R. +) Xét với \(m=1\) ta có: \(y'=-{{x}^{2}}-2x-1=-{{\left( x+1 \right)}^{2}}\le 0\,\,\forall x\in R\Rightarrow m=1\) thì hàm số nghịch biến trên R. Chọn B. Câu hỏi 25 : Hàm số \(y={{x}^{3}}-6{{x}^{2}}+mx+1\) đồng biến trên \(\left( 0;+\infty \right)\) khi giá trị của \(m\) là:
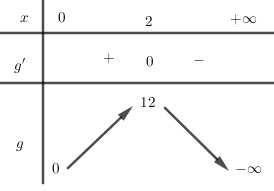
Đáp án: A Phương pháp giải: Hàm số \(y=a{{x}^{3}}+b{{x}^{2}}+cx+d,\,\left( a\ne 0 \right)\)đồng biến trên \(\left( p;q \right)\) khi và chỉ khi \({y}'\ge 0,\,\forall x\in \left( p;q \right)\). Lời giải chi tiết: Ta có \({y}'=3{{x}^{2}}-12x+m\). Để hàm số đồng biến trên \(\left( 0;+\infty \right)\) thì \({y}'\ge 0\,,\forall x>0\)\(\Leftrightarrow 3{{x}^{2}}-12x+m\ge 0,\,\forall x>0\Leftrightarrow -3{{x}^{2}}+12x\le m,\forall x>0\). (*) Xét \(y=g\left( x \right)=-3{{x}^{2}}+12x\) với \(x>0\). Ta có \({g}'\left( x \right)=-6x+12=0\Leftrightarrow x=2\)(TM). BBT \(y=g\left( x \right)\) với \(x>0\).
Từ BBT ta có \(\underset{\left( 0;+\infty \right)}{\mathop{\max }}\,g\left( x \right)=12\), từ (*) suy ra \(m\ge \underset{\left( 0;+\infty \right)}{\mathop{\max }}\,g\left( x \right)=12\Leftrightarrow m\ge 12\). Chọn A.
Câu hỏi 26 : Tìm tất cả các giá trị thực của tham số \(m\) sao cho hàm số \(y=\frac{mx+4}{x+m}\) nghịch biến trên khoảng \(\left( -\,\infty ;1 \right).\)
Đáp án: D Phương pháp giải: Dựa vào điều kiện để hàm số b1 trên b1 đồng biến hoặc nghịch biến trên khoảng Lời giải chi tiết: Ta có \(y=\frac{mx+4}{x+m}\Rightarrow {y}'=\frac{{{m}^{2}}-4}{{{\left( x+m \right)}^{2}}};\,\,\forall x\ne -\,m.\) Yêu cầu bài toán \( \Leftrightarrow \left\{ \begin{array}{l}y' < 0\\x = - m \notin \left( { - \infty ;1} \right)\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{m^2} - 4 > 0\\ - m \ge 1\end{array} \right. \Leftrightarrow - 2 < m \le - 1.\) Chọn D Câu hỏi 27 : Cho hàm số \(y=f(x)\) có đạo hàm \({f}'(x)={{x}^{2}}-2x,\,\,\forall x\in \mathbb{R}.\) Hàm số \(y=-2f(x)\) đồng biến trên khoảng
Đáp án: A Phương pháp giải: +) Hàm số \(y=f\left( x \right)\) đồng biến trên \(R\Leftrightarrow y'\ge 0\) với mọi \(x\in R\). Lời giải chi tiết: Ta có \( y’=-2f’(x) > 0 \Leftrightarrow f’(x) < 0 \Leftrightarrow x^2-2x<0 \Leftrightarrow 0<x<2\) Chọn A. Câu hỏi 28 : Hàm số \(y=\sqrt{8+2x-{{x}^{2}}}\) đồng biến trên khoảng nào dưới đây?
Đáp án: D Phương pháp giải: - Tìm điều kiện xác định. - Tính đạo hàm của hàm số. - Tìm nghiệm của y’ (nếu có). - Lập bảng xét dấu y’. - Kết luận. Lời giải chi tiết: Điều kiện xác định: \(8+2x-{{x}^{2}}\ge 0\Leftrightarrow -2\le x\le 4\) \(\begin{array}{l}y = \sqrt {8 + 2x - {x^2}} \Rightarrow y' = \frac{{(8 + 2x - {x^2})'}}{{2\sqrt {8 + 2x - {x^2}} }} = \frac{{2 - 2x}}{{2\sqrt {8 + 2x - {x^2}} }} = \frac{{1 - x}}{{\sqrt {8 + 2x - {x^2}} }}\\y' = 0 \Leftrightarrow x = 1\end{array}\) Bảng xét dấu y’: Vậy hàm số đồng biến trên khoảng \(\left( -2;1 \right).\) Chọn: D. Câu hỏi 29 : Cho hàm số \(y=f\left( x \right)\) có đạo hàm \({f}'\left( x \right)={{\left( x+1 \right)}^{2}}\left( 2-x \right)\left( x+3 \right).\) Mệnh đề nào dưới đây đúng?
Đáp án: D Phương pháp giải: Dựa vào bảng biến thiên để xác định các khoảng đơn điệu của hàm số Lời giải chi tiết: Ta có \(\left\{ \begin{array}{l}f'\left( x \right) > 0 \Leftrightarrow - 3 < x < 2\\f'\left( x \right) < 0 \Leftrightarrow \left[ \begin{array}{l}x > 2\\x < - 3\end{array} \right.\end{array} \right..\) Suy ra hàm số đồng biến trên khoảng \(\left( -\,3;\,2 \right),\) nghịch biến trên các khoảng \(\left( -\,\infty ;\,-3 \right)\) và \(\left( 2;\,+\infty \right).\) Chọn D Câu hỏi 30 : Cho hàm số \(y = x - \cos x\). Khẳng định nào dưới đây là ĐÚNG?
Đáp án: A Phương pháp giải: Hàm số \(y = f\left( x \right)\) đồng biến trên R \( \Leftrightarrow y' \ge 0\,\,\forall x \in R\) và \(y' = 0\) tại hữu hạn điểm. Lời giải chi tiết: TXĐ: D = R. Ta có: \(\eqalign{ & y' = 1 + \sin x \ge 0\,\,\forall x \in R \cr & y' = 0 \Leftrightarrow \sin x = - 1 \Leftrightarrow x = - {\pi \over 2} + k2\pi \,\,\left( {k \in Z} \right) \cr} \) \( \Rightarrow y' = 0\) tại hữu hạn điểm. Vậy hàm số đồng biến trên R. Chọn A. Quảng cáo
|














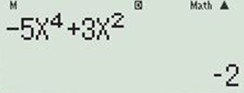
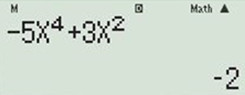
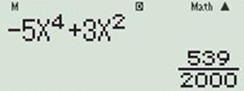

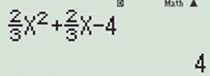
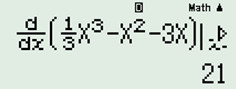 \(>0\Rightarrow A\) sai.
\(>0\Rightarrow A\) sai.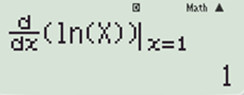 \(\Rightarrow \) đáp án B \( y’ = 1 > 0 \Rightarrow B\) sai.
\(\Rightarrow \) đáp án B \( y’ = 1 > 0 \Rightarrow B\) sai.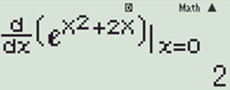 \(\Rightarrow C\) sai.
\(\Rightarrow C\) sai.