30 bài tập trắc nghiệm các định nghĩa về véc tơLàm bàiQuảng cáo
Câu hỏi 1 : Cho tam giác \(ABC\) có \(M,N,P\) lần lượt là trung điểm của \(AB,AC,BC\). Khi đó, các vectơ đối của vectơ \(\overrightarrow {PN} \) là
Đáp án: D Phương pháp giải: \(\overrightarrow a ,\,\,\overrightarrow b \) đối nhau khi chúng cùng phương, ngược hướng và cùng độ dài. Lời giải chi tiết:
Các vectơ đối của vectơ \(\overrightarrow {PN} \) là: \(\overrightarrow {AM} \), \(\overrightarrow {MB} \), \(\overrightarrow {NP} \). Chọn: D. Câu hỏi 2 : Cho ba điểm \(A,\,\,B,\,\,C\) phân biệt. Có bao nhiêu vectơ khác vectơ – không tạo bởi hai trong số ba điểm đó?
Đáp án: A Phương pháp giải: Từ hai điểm phân biệt ta luôn tạo được 2 vecto khác vecto – không. Lời giải chi tiết: Từ hai điểm phân biệt ta luôn tạo được 2 vecto khác vecto – không. Vậy từ ba điểm, ta tạo được sáu vectơ khác vectơ không. Chọn A. Câu hỏi 3 : Điều kiện cần và đủ để \(\overrightarrow {AB} = \overrightarrow {CD} \) là các vectơ \(\overrightarrow {AB} \) và \(\overrightarrow {CD} \) thỏa mãn
Đáp án: C Phương pháp giải: Hai véc tơ bằng nhau nếu chúng cùng hướng và cùng độ lớn. Lời giải chi tiết: Điều kiện cần và đủ để \(\overrightarrow {AB} = \overrightarrow {CD} \) là chúng cùng hướng và cùng độ dài. Chọn C. Câu hỏi 4 : Cho tam giác \(ABC\) đều, tâm \(O,\,\,M\) là trung điểm của \(BC.\) Góc \(\left( {\overrightarrow {OM} ,\overrightarrow {AB} } \right)\) bằng:
Đáp án: B Phương pháp giải: Sử dụng tính chất của tam giác đều. Lời giải chi tiết: Vì tam giác \(ABC\) đều nên \(\left( {\overrightarrow {OM} ,\overrightarrow {AB} } \right) = \left( {\overrightarrow {AM} ,\overrightarrow {AB} } \right) = \angle BAM = 30^\circ .\) Chọn B. Câu hỏi 5 : Cho hình bình hành ABCD, O là giao điểm hai đường chéo. Khẳng định nào sau đây đúng?
Đáp án: C Phương pháp giải: Sử dụng tính chất hình bình hành. Lời giải chi tiết: Vì \(O\) là trung điểm \(AC\) nên \(\overrightarrow {AO} = \overrightarrow {OC} .\) Chọn C. Câu hỏi 6 : Cho tam giác ABC, gọi M, N lần lượt là trung điểm của hai cạnh AB và AC. Mệnh đề nào sau đây đúng?
Đáp án: C Phương pháp giải: Sử dụng tính chất đường trung bình của tam giác. Lời giải chi tiết: M, N lần lượt là trung điểm của hai cạnh AB và AC nên MN là đường trung bình của tam giác ABC \( \Rightarrow MN\,{\rm{//}}\,BC\) nên \(\overrightarrow {MN} \) cùng phương với \(\overrightarrow {BC} .\) Chọn C. Câu hỏi 7 : Cho \(\overrightarrow a \) và \(\overrightarrow b \) là các vectơ khác \(\overrightarrow 0 \) sao cho \(\overrightarrow a = \frac{{2018}}{{2019}}\overrightarrow b \). Khẳng định nào sau đây sai?
Đáp án: B Phương pháp giải: Ta có: \(\left| {k.\overrightarrow a } \right| = k.\left| {\overrightarrow a } \right|.\) Lời giải chi tiết: Ta có: \(\overrightarrow a = \frac{{2018}}{{2019}}\overrightarrow b \Rightarrow k = \frac{{2018}}{{2019}} > 0 \Rightarrow \overrightarrow a ,\,\,\overrightarrow b \) cùng hướng. \( \Rightarrow \) Đáp án A và C đúng. \( \Rightarrow \left| {\overrightarrow a } \right| = \left| {\frac{{2018}}{{2019}}\overrightarrow b } \right| = \frac{{2018}}{{2019}}\left| {\overrightarrow b } \right| < \left| {\overrightarrow b } \right|.\) Chọn B. Câu hỏi 8 : Cho hình bình hành \(ABCD,\) vectơ có điểm đầu và điểm cuối là các đỉnh của hình bình hành bằng với vectơ \(\overrightarrow {AB} \) là:
Đáp án: A Phương pháp giải: Hai vecto bằng nhau có cùng chiều và cùng độ lớn. Lời giải chi tiết: Ta có: \(ABCD\) là hình bình hành \( \Rightarrow \overrightarrow {DC} = \overrightarrow {AB} .\) Chọn A. Câu hỏi 9 : Cho bốn điểm \(A, \,B, \,C,\, D\) phân biệt. Số vectơ (khác \(\overrightarrow 0 \)) có điểm đầu và điểm cuối lấy từ các điểm \(A,\, B,\, C,\, D\) là
Đáp án: D Phương pháp giải: Đếm lần lượt số vectơ tạo thành từ các điểm.
Lời giải chi tiết: Có ba vectơ có điểm đầu là \(A\) là: \(\overrightarrow {AB,} \,\,\overrightarrow {AC} ,\,\,\overrightarrow {AD} .\) Tương tự cũng có mỗi điểm \(B,\,\,C,\,\,D\) cũng có thể tạo nên ba vectơ với \(B,\,\,C,\,\,D\) là các điểm đầu. Vậy có thể tạo thành 12 vectơ. Chọn D. Câu hỏi 10 : Cho bốn điểm A, B, C, D phân biệt. Nếu \(\overrightarrow {AB} = \overrightarrow {BC} \) thì có nhận xét gì về ba điểm A, B, C
Đáp án: A Phương pháp giải: \(\overrightarrow {AB} = \overrightarrow {CD} \Leftrightarrow \left\{ \begin{array}{l}AB//CD\\AB = CD\\\overrightarrow {AB} \nearrow \nearrow \overrightarrow {CD} \end{array} \right.\) Lời giải chi tiết: Cho bốn điểm A, B, C, D phân biệt. Nếu \(\overrightarrow {AB} = \overrightarrow {BC} \) thì B là trung điểm của AC Chọn A. Câu hỏi 11 : Cho hình thoi \(ABCD\) có tâm \(O\). Hãy cho biết số khẳng định đúng ? a) \(\overrightarrow {AB} = \overrightarrow {BC} \) b) \(\overrightarrow {AB} = \overrightarrow {DC} \) c) \(\overrightarrow {OA} = - \overrightarrow {OC} \) d) \(\overrightarrow {OB} = \overrightarrow {OA} \) e) \(\left| {\overrightarrow {AB} } \right| = \left| {\overrightarrow {BC} } \right|\) f) \(2\left| {\overrightarrow {OA} } \right| = \left| {\overrightarrow {BD} } \right|\)
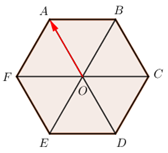
Đáp án: A Phương pháp giải: Hai vectơ bằng nhau nếu chúng cùng hướng và cùng độ dài. \(\left| {\overrightarrow {AB} } \right| = AB\) Lời giải chi tiết: a) Sai b) Đúng c) Đúng d) Sai e) Sai f) Đúng Vậy có 3 khẳng định đúng Chọn A. Câu hỏi 12 : Cho lục giác đều \(ABCDEF\) tâm \(O\). Hãy tìm các vectơ khác vectơ-không có điểm đầu, điểm cuối là đỉnh của lục giác và tâm O sao cho ngược hướng với \(\overrightarrow {OC} \)
Đáp án: C Phương pháp giải: Giá của 2 vectơ song song hoặc trùng nhau thì hai vectơ đó cùng phương. Hai vectơ cùng phương hoặc là cùng hướng, hoặc là ngược hướng. Lời giải chi tiết: Cho lục giác đều \(ABCDEF\) tâm \(O\). Các vectơ khác vectơ-không có điểm đầu, điểm cuối là đỉnh của lục giác và tâm O sao cho ngược hướng với \(\overrightarrow {OC} \) là \(\overrightarrow {CO} ,\,\overrightarrow {OF} ,\,\overrightarrow {BA} ,\,\overrightarrow {DE} \) Chọn C. Câu hỏi 13 : Cho \(\overrightarrow {AB} \) ≠ \(\vec 0\) và một điểm \(C,\) có bao nhiêu điểm \(D\) thỏa mãn: \(\left| {\overrightarrow {AB} } \right| = \left| {\overrightarrow {C{\rm{D}}} } \right|\)
Đáp án: D Phương pháp giải: \(\left| {\overrightarrow {AB} } \right| = AB\) Lời giải chi tiết: Cho \(\overrightarrow {AB} \) ≠ \(\vec 0\) và một điểm \(C,\) có vô số điểm \(D\) thỏa mãn: \(\left| {\overrightarrow {AB} } \right| = \left| {\overrightarrow {C{\rm{D}}} } \right|\) Tập hợp các điểm D thỏa mãn đề bài là đường tròn tâm C bán kính \(R = AB\) Chọn D. Câu hỏi 14 : Cho bốn điểm A, B, C, D phân biệt. Nếu \(\overrightarrow {AB} = \overrightarrow {DC} \) thì có nhận xét gì về bốn điểm A, B, C, D.
Đáp án: B Phương pháp giải: Hai vectơ bằng nhau nếu chúng cùng hướng và cùng độ dài. Lời giải chi tiết: Cho bốn điểm A, B, C, D phân biệt. Nếu \(\overrightarrow {AB} = \overrightarrow {DC} \Rightarrow \left\{ \begin{array}{l}AB//DC\\AB = DC\end{array} \right. \Rightarrow ABCD\) là hình bình hành. Chọn B. Câu hỏi 15 : Cho ba điểm A, B, C phân biệt thẳng hàng. Khi nào thì hai vectơ \(\overrightarrow {AB} \) và \(\overrightarrow {AC} \) cùng hướng ?
Đáp án: C Phương pháp giải: Hai vectơ có giá song song hoặc trùng nhau gọi là hai vectơ cùng phương . Hai vectơ cùng phương thì hoặc cùng hướng hoặc ngược hướng. Lời giải chi tiết: Cho ba điểm \(A,\,\,B,\,\,C\) phân biệt thẳng hàng, hai vectơ \(\overrightarrow {AB} \) và \(\overrightarrow {AC} \) cùng hướng \( \Leftrightarrow A\) nằm ngoài đoạn BC Chọn C. Câu hỏi 16 : Cho hình bình hành \(ABCD\) có tâm là O. Tìm các vectơ từ 5 điểm A, B, C, D, O bằng vectơ \(\overrightarrow {AB} ;\,\,\,\,\overrightarrow {OB} \)
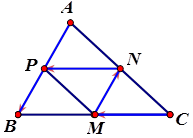
Đáp án: D Phương pháp giải: Hai vectơ bằng nhau nếu chúng cùng hướng và cùng độ dài. Lời giải chi tiết: \(\overrightarrow {AB} = \overrightarrow {DC} ,\,\,\overrightarrow {OB} = \overrightarrow {DO} \) Chọn D. Câu hỏi 17 : Cho tam giác \(ABC\). Gọi \(M,\,N,\,P\) lần lượt là trung điểm của \(BC,\,CA,\,AB\). Có bao nhiêu vectơ khác vectơ - không cùng hướng với \(\overrightarrow {AB} \) có điểm đầu và điểm cuối lấy trong điểm đã cho.
Đáp án: A Phương pháp giải: Hai vectơ có giá song song hoặc trùng nhau gọi là hai vectơ cùng phương Hai vectơ cùng phương thì hoặc cùng hướng hoặc ngược hướng. Lời giải chi tiết: Các vectơ khác vectơ - không cùng hướng với \(\overrightarrow {AB} \) là \(\overrightarrow {AP} ,\,\,\overrightarrow {PB} ,\,\,\overrightarrow {NM} \). Vậy có 3 vectơ thỏa mãn yêu cầu đề bài Chọn A. Câu hỏi 18 : Biết điểm M là trung điểm của đoạn thẳng AB. Mệnh đề nào sau đây đúng?
Đáp án: A Phương pháp giải: M là trung điểm của AB \( \Rightarrow \overrightarrow {MA} + \overrightarrow {MB} = \overrightarrow 0 \) Lời giải chi tiết: M là trung điểm của AB \( \Rightarrow \overrightarrow {MA} + \overrightarrow {MB} = \overrightarrow 0 \Rightarrow \overrightarrow {MA} = - \overrightarrow {MB} = \overrightarrow {BM} \) Chọn A. Câu hỏi 19 : Hai \(\overrightarrow a \) và \(\overrightarrow b \) bằng nhau nếu chúng:
Đáp án: B Phương pháp giải: Hai vectơ bằng nhau là hai vectơ có cùng hướng và có độ dài bằng nhau. Lời giải chi tiết: Hai vectơ bằng nhau là hai vectơ có cùng hướng và có độ dài bằng nhau. Chọn B. Câu hỏi 20 : Cho hình bình hành \(ABCD\). Đẳng thức nào sau đây sai.
Đáp án: A Phương pháp giải: Độ dài vectơ chính là độ dài đoạn thẳng. Lời giải chi tiết: Vì ABCD là hình bình hành nên \(AC \ne BD \Rightarrow \left| {\overrightarrow {AC} } \right| \ne \left| {\overrightarrow {BD} } \right|\). Vậy đẳng thức A sai. Chọn A. Câu hỏi 21 : Cho 6 điểm phân biệt. Hỏi có mấy vectơ khác vectơ - không mà có điểm đầu và điểm cuối lấy từ 6 điểm đó?
Đáp án: C Phương pháp giải: Liệt kê các cặp điểm có được từ 6 điểm. Với mỗi cặp điểm ta sẽ được hai vectơ khác vectơ – không. Lời giải chi tiết: Từ 6 điểm phân biệt ta sẽ có được 15 cặp điểm khác nhau. Với mỗi cặp điểm ta sẽ được hai vectơ khác vectơ – không nên từ 6 điểm đó tạo được 30 vectơ khác vectơ – không. Chọn C. Câu hỏi 22 : Điều kiện nào là điều kiện cần và đủ để \(\overrightarrow {AB} = \overrightarrow {CD} \):
Đáp án: C Phương pháp giải: \(\overrightarrow {AB} = \overrightarrow {CD} \Leftrightarrow \left\{ \begin{array}{l}AB//CD\\AB = CD\\\overrightarrow {AB} \nearrow \nearrow \overrightarrow {CD} \end{array} \right.\) Lời giải chi tiết: \(\overrightarrow {AB} = \overrightarrow {CD} \Leftrightarrow \left\{ \begin{array}{l}AB//CD\\AB = CD\\\overrightarrow {AB} \nearrow \nearrow \overrightarrow {CD} \end{array} \right. \Leftrightarrow ABDC\) là hình bình hành \( \Leftrightarrow \) \(AD\) và \(BC\)có cùng trung điểm Chọn C. Câu hỏi 23 : Cho trước hai điểm \(A,\,B\) phân biệt . Tìm tập hợp các điểm M thoả mãn \(\left| {\overrightarrow {MA} } \right| = \left| {\overrightarrow {MB} } \right|\).
Đáp án: B Phương pháp giải: \(\left| {\overrightarrow {MA} } \right| = MA\) Lời giải chi tiết: \(\left| {\overrightarrow {MA} } \right| = \left| {\overrightarrow {MB} } \right| \Leftrightarrow MA = MB \Rightarrow \)Tập hợp điểm \(M\) là đường trung trực của đoạn thẳng \(AB\) Chọn B. Câu hỏi 24 : Cho tam giác \(ABC\) đều cạnh \(a\) và \(G\) là trọng tâm. Gọi \(I\) là trung điểm của \(AG\). Tính độ dài của các vectơ \(\overrightarrow {BI} \).
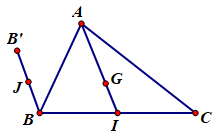
Đáp án: B Phương pháp giải: \(\left| {\overrightarrow {BI} } \right| = BI\) Lời giải chi tiết: Ta có \(\left| {\overrightarrow {AB} } \right| = AB = a\) Gọi M là trung điểm của \(BC\) Ta có: \(\left| {\overrightarrow {AG} } \right| = AG = \frac{2}{3}AM = \frac{2}{3}\sqrt {A{B^2} - B{M^2}} = \frac{2}{3}\sqrt {{a^2} - {{\frac{a}{4}}^2}} = \frac{{a\sqrt 3 }}{3}\) \(\left| {\overrightarrow {BI} } \right| = BI = \sqrt {B{M^2} + M{I^2}} = \sqrt {\frac{{{a^2}}}{4} + \frac{{{a^2}}}{3}} = \frac{{a\sqrt {21} }}{6}\) Chọn B. Câu hỏi 25 : Cho tam giác \(ABC\) có trọng tâm \(G\). Gọi \(I\) là trung điểm của \(BC\). Dựng điểm \(B'\) sao cho \(\overrightarrow {B'B} = \overrightarrow {AG} \). Gọi \(J\) là trung điểm của \(BB'\). Khẳng định nào sau đây là đúng?
Đáp án: B Phương pháp giải: So sánh hướng và độ dài của \(\overrightarrow {BJ} ,\,\,\overrightarrow {IG} \) Lời giải chi tiết: Ta có \(\overrightarrow {B'B} = \overrightarrow {AG} \) suy ra \(B'B = AG\) và \(BB'//AG\). Do đó \(\overrightarrow {BJ} ,\,\,\overrightarrow {IG} \) cùng hướng (1). Vì \(G\) là trọng tâm tam giác \(ABC\) nên \(IG = \frac{1}{2}AG\), \(J\) là trung điểm \(BB'\) suy ra \(BJ = \frac{1}{2}BB'\) Vì vậy \(BJ = IG\) (2) Từ (1) và (2) ta có \(\overrightarrow {BJ} = \overrightarrow {IG} \). Chọn B. Câu hỏi 26 : Cho tứ giác \(ABCD\). Gọi M, N, P, Q lần lượt là trung điểm AB, BC, CD, DA. Khăng định nào sau đây đúng
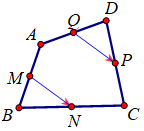
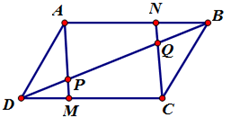
Đáp án: B Phương pháp giải: Tìm n bất kỳ để \(\frac{{n(n + 1)}}{2}\) chia hết cho 11 Lời giải chi tiết: Do M, Q lần lượt là trung điểm của AB và AD nên MQ là đường trung bình của tam giác \(ABD\) suy ra \(MQ//BD\) và \(MQ = \frac{1}{2}BD\) (1). Tương tự NP là đường trung bình của tam giác \(CBD\) suy ra \(NP//BD\) và \(NP = \frac{1}{2}BD\) (2). Từ (1) và (2) suy ra \(MQ//NP\) và \(NP = MQ\) do đó tứ giác \(MNPQ\) là hình bình hành Vậy ta có \(\overrightarrow {MQ} \, = \,\overrightarrow {NP} \,\). Chọn B. Câu hỏi 27 : Cho hình bình hành \(ABCD\). Trên các đoạn thẳng\(DC,\,\,AB\) theo thứ tự lấy các điểm \(M,\,\,N\) sao cho \(DM = BN\). Gọi \(P\) là giao điểm của \(AM,\,\,DB\) và \(Q\) là giao điểm của \(CN,\,\,DB\). Khẳng định nào sau đây là đúng?
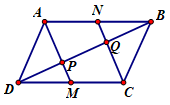
Đáp án: A Phương pháp giải: Chứng minh tứ giác \(ANCM\) là hình bình hành, \(\Delta DMP = \Delta BNQ\) (c.g.c) để so sánh độ dài các vectơ từ đó xét hướng để đưa ra kết luận. Lời giải chi tiết: Ta có \(DM = BN \Rightarrow AN = MC\), mặt khác \(AN\) song song với \(MC\) do đó tứ giác \(ANCM\) là hình bình hành Suy ra \(\overrightarrow {AM} = \overrightarrow {NC} \). Ta có: \(\angle DMP = \angle APB\) (đối đỉnh) và \(\angle APQ = \angle NQB\) (hai góc đồng vị) \( \Rightarrow \angle DMP = \angle BNQ\,\,\,\left( { = \angle APB} \right)\). Xét tam giác \(\Delta DMP\) và \(\Delta BNQ\) ta có: \(\begin{array}{l}DM = NB\,\,\,\left( {gt} \right)\\\angle PDM = \angle QBN\,\,\,\left( {so\,\,le\,\,\,trong} \right)\\ \Rightarrow \Delta DMP = \Delta BNQ\,\,\,\,\left( {c - g - c} \right).\end{array}\) \( \Rightarrow DP = QB\) (hai cạnh tương ứng). Do đó \(\Delta DMP = \Delta BNQ\) (c.g.c) suy ra \(DP = QB\). Dễ thấy \(\overrightarrow {DP} ,\,\,\overrightarrow {QB} \) cùng hướng vì vậy \(\overrightarrow {DP} = \overrightarrow {QB} \). Chọn A. Câu hỏi 28 : Cho hình bình hành \(ABCD\). Gọi \(M,\,N\) lần lượt là trung điểm của \(DC,\,AB\); \(P\) là giao điểm của \(AM,\,\,DB\) và \(Q\) là giao điểm của \(CN,\,\,DB\).Khẳng định nào sau đây là đúng nhất.
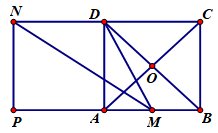
Đáp án: C Phương pháp giải: Chứng minh tứ giác \(DMBN\) là hình bình hành. So sánh độ dài các đoạn DP, PQ, QB Lời giải chi tiết: Ta có tứ giác \(DMBN\) là hình bình hành vì \(DM = NB = \frac{1}{2}AB,\,\,DM//NB\). Suy ra \(\overrightarrow {DM} = \overrightarrow {NB} \). Xét tam giác \(CDQ\) có \(M\) là trung điểm của \(DC\) và \(MP//QC\) do đó \(P\) là trung điểm của \(DQ\). Tương tự xét tam giác \(ABP\) suy ra được \(Q\) là trung điểm của \(PB\) Vì vậy \(DP = PQ = QB\) từ đó suy ra \(\overrightarrow {DP} = \overrightarrow {PQ} = \overrightarrow {QB} \) Chọn C. Câu hỏi 29 : Cho hình vuông \(ABCD\) tâm \(O\) cạnh \(a\). Gọi \(M\)là trung điểm của \(AB\), \(N\) là điểm đối xứng với \(C\) qua \(D\). Hãy tính độ dài của vectơ \(\overrightarrow {MN} \).
Đáp án: A Phương pháp giải: \(\left| {\overrightarrow {MN} } \right| = MN\) Lời giải chi tiết: Áp dụng định lý Pitago trong tam giác vuông \(MAD\) ta có \(D{M^2} = A{M^2} + A{D^2} = {\left( {\frac{a}{2}} \right)^2} + {a^2} = \frac{{5{a^2}}}{4}\)\( \Rightarrow DM = \frac{{a\sqrt 5 }}{2}\) Suy ra \(\left| {\overrightarrow {MD} } \right| = MD = \frac{{a\sqrt 5 }}{2}\). Qua N kẻ đường thẳng song song với \(AD\) cắt\(AB\) tại \(P\). Khi đó tứ giác \(ADNP\) là hình vuông và \(PM = PA + AM = a + \frac{a}{2} = \frac{{3a}}{2}\). Áp dụng định lý Pitago trong tam giác vuông \(NPM\) ta có \(M{N^2} = N{P^2} + P{M^2} = {a^2} + {\left( {\frac{{3a}}{2}} \right)^2} = \frac{{13{a^2}}}{4}\)\( \Rightarrow DM = \frac{{a\sqrt {13} }}{2}\) Suy ra \(\left| {\overrightarrow {MN} } \right| = MN = \frac{{a\sqrt {13} }}{2}\). Chọn A. Câu hỏi 30 : Cho tam giác \(ABC\) có trực tâm H và O tâm là đường tròn ngoại tiếp . Gọi B' là điểm đối xứng B qua O. Khẳng định nào sau đây là đúng?
Đáp án: A Phương pháp giải: Chứng minh AHCB’ là hbh do có 2 cặp cạnh đối song song Lời giải chi tiết: Ta có \(B'C \bot BC\) (do \(\Delta BCB'\) có trung tuyến \(OC = OB = \frac{1}{2}BB'\) nên vuông tại C)\(,\,\,AH \bot BC \Rightarrow B'C//AH\), \(B'A \bot BA,\,\,CH \bot AB \Rightarrow B'A//CH\) Suy ra \(AHCB'\) là hình bình hành do đó \(\overrightarrow {AH} \,\, = \,\overrightarrow {B'C} \). Chọn A. Quảng cáo
|