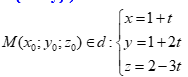30 bài tập phương trình đường thẳng trong không gian mức độ vận dụng caoLàm bàiQuảng cáo
Câu hỏi 1 : Trong không gian với hệ tọa độ Oxyz, cho hai điểm \(A\left( 3;3;1 \right),B\left( 0;2;1 \right)\) và mặt phẳng \(\left( P \right):\,\,x+y+z-7=0\). Đường thẳng d nằm trong (P) sao cho mọi điểm của d cách đều hai điểm A, B có phương trình :
Đáp án: C Phương pháp giải: +) Mọi điểm thuộc d cách đều 2 điểm A, B nên d nằm trong mặt phẳng trung trực \(\left( \alpha \right)\) của AB. +) Khi đó \(d=\left( P \right)\cap \left( \alpha \right)\) Lời giải chi tiết: Gọi I là trung điểm của AB ta có: \(\left\{ \begin{array}{l}{x_I} = \frac{{{x_A} + {x_B}}}{2} = \frac{{3 + 0}}{2} = \frac{3}{2}\\{y_I} = \frac{{{y_A} + {y_B}}}{2} = \frac{{3 + 2}}{2} = \frac{5}{2}\\{z_I} = \frac{{{z_A} + {z_B}}}{2} = \frac{{1 + 1}}{2} = 1\end{array} \right. \Rightarrow I\left( {\frac{3}{2};\frac{5}{2};1} \right)\) \(\overrightarrow{AB}=\left( -3;-1;0 \right)\) Gọi \(\left( \alpha \right)\) là mặt phẳng trung trực của AB, khi đó \(\left( \alpha \right)\) có phương trình \(-3\left( x-\frac{3}{2} \right)-1\left( y-\frac{5}{2} \right)=0\Leftrightarrow -3x-y+7=0\) Vì mọi điểm thuộc d đều cách đều A, B nên \(d\subset \left( \alpha \right)\Rightarrow d=\left( P \right)\cap \left( \alpha \right)\Rightarrow \) Tập hợp các điểm thuộc d là nghiệm của hệ phương trình : \(\left\{ \begin{array}{l}x + y + z - 7 = 0\\ - 3x - y + 7 = 0\end{array} \right.\) Chọn z = 2t ta có : \(\left\{ \begin{array}{l}x + y = 7 - 2t\\ - 3x - y = - 7\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l} - 2x = - 2t\\y = - 3x + 7\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = t\\y = 7 - 3t\end{array} \right.\) \( \Rightarrow \left\{ \begin{array}{l}x = t\\y = 7 - 3t\\z = 2t\end{array} \right.\) là phương trình đường thẳng cần tìm. Chọn C. Câu hỏi 2 : Trong không gian với hệ tọa độ Oxyz, cho hai điểm \(A\left( 4;6;2 \right);\,\,B\left( 2;-2;0 \right)\) vằ mặt phẳng \(\left( P \right):\,\,x+y+z=0\). Xét đường thẳng d thay đổi thuộc (P) và đi qua B, gọi H là hình chiếu vuông góc của A trên d. Biết rằng khi d thay đổi H thuộc một đường tròn cố định. Tính bán kính R của đường tròn đó.
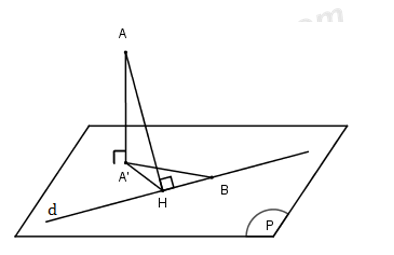
Đáp án: A Phương pháp giải: +) Gọi A’ là hình chiếu của A trên (P), điểm A’ cố định. +) Chứng minh \(\widehat{A'HB}={{90}^{0}}\Rightarrow \) H thuộc đường tròn đường kính A’B không đổi khi d thay đổi. +) Khi đó \(R=\frac{A'B}{2}\) Lời giải chi tiết:
Dễ thấy \(B\in \left( P \right)\) Gọi A’ là hình chiếu của A trên mp(P), A’ cố định. Ta có \(\left\{ {\begin{array}{*{20}{l}}{{\rm{A}}{{\rm{A}}^\prime } \bot d}\\{AH \bot d}\end{array}} \right. \Rightarrow d \bot \left( {AA'H} \right) \Rightarrow d \bot A'H \Rightarrow \widehat {A'HB} = {90^0}\) \(\Rightarrow\) khi d thay đổi điểm H luôn thuộc đường tròn đường kính A’B cố định. Trước hết ta viết phương trình đường thẳng AA’ qua A và vuông góc với (P) nên nhận \({{\overrightarrow{n}}_{\left( P \right)}}=\left( 1;1;1 \right)\) là 1 VTCP nên có phương trình \(\left\{{\begin{array}{*{20}{l}}{x = 4 + t}\\{y = 6 + t}\\{z = 2 + t}\end{array}} \right.\) \(\begin{array}{l}A' \in AA' \Rightarrow A'\left( {4 + t;6 + t;2 + t} \right);A' \in \left( P \right) \Rightarrow 4 + t + 6 + t + 2 + t = 0 \Leftrightarrow 3t + 12 = 0 \Leftrightarrow t = - 4\\ \Rightarrow A'\left( {0;2; - 2} \right)\end{array}\) Khi đó \(A'B=\sqrt{{{\left( 2-0 \right)}^{2}}+{{\left( -2-2 \right)}^{2}}+{{\left( 0+2 \right)}^{2}}}=2\sqrt{6}\) Vậy H luôn thuộc đường tròn cố định có bán kính \(R=\frac{A'B}{2}=\sqrt{6}\) Chọn A. Câu hỏi 3 : Trong không gian với hệ tọa độ \(Oxyz,\) cho hai đường thẳng \({{d}_{1}}:\frac{x-1}{1}=\frac{y-2}{2}=\frac{z-1}{-\,1}\) và \({{d}_{2}}:\left\{ \begin{align} x=2-t \\ y=3-t \\ z=-\,2 \\ \end{align} \right..\) Mặt phẳng \(\left( P \right):x+by+cz+d=0\) (với \(b,\,\,c,\,\,d\in \mathbb{R}\)) vuông góc với đường thẳng \({{d}_{1}}\) và chắn \({{d}_{1}},\,\,{{d}_{2}}\) đoạn thẳng có độ dài nhỏ nhất. Tổng \(b+c+d\) bằng
Đáp án: C Phương pháp giải: Khai thác tối đa dữ kiện của bài toán để tìm vectơ pháp tuyến của mặt phẳng và thông qua bài toán tìm điểm xác định giá trị nhỏ nhất của độ dài đường thẳng Lời giải chi tiết: Vì \(\left( P \right)\bot {{d}_{1}}\) suy ra \({{\vec{n}}_{\left( P \right)}}\)//\({{\vec{u}}_{{{d}_{1}}}}\)\(\Rightarrow \)\(\frac{1}{1}=\frac{b}{2}=\frac{c}{-\,1}\Rightarrow \left\{ \begin{align} b=2 \\ c=-\,1 \\ \end{align} \right.\Rightarrow \left( P \right):x+2y-z+d=0.\) Gọi \(A\in {{d}_{1}}\Rightarrow A\left( a+1;2a+2;1-a \right)\) và \(B\in {{d}_{2}}\Rightarrow B\left( 2-m;3-m;-\,2 \right).\) Mà \(A,\,\,B\in mp\,\,\left( P \right)\) suy ra \(\left\{ \begin{array}{l}a + 1 + 2\left( {2a + 2} \right) - \left( {1 - a} \right) + d = 0\\2 - m + 2\left( {3 - m} \right) + 2 + d = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}6a + d + 4 = 0\left( 1 \right)\\ - 3m + d + 10 = 0\left( 2 \right)\end{array} \right.\) Lấy \(\left( 1 \right)-\left( 2 \right),\) ta được \(2a+m=2\Leftrightarrow m=2-2a\)\(\Rightarrow \)\(A{{B}^{2}}={{\left( 1-m-a \right)}^{2}}+{{\left( 1-m-2a \right)}^{2}}+{{\left( a-3 \right)}^{2}}\) \(={{\left( a-1 \right)}^{2}}+{{\left( -\,1 \right)}^{2}}+{{\left( a-3 \right)}^{2}}=2{{a}^{2}}-8a+11=2{{\left( a-2 \right)}^{2}}+3\ge 3\Rightarrow AB\ge \sqrt{3}.\) Dấu \(''\,\,=\,\,''\) xảy ra khi và chỉ khi \(a=2,\) thay vào \(\left( 1 \right),\) ta được \(d=-\,6a-4=-\,16.\) Vậy tổng \(T=b+c+d=2-1-16=-\,15.\) Chọn C Câu hỏi 4 : Cho đường thẳng \(d:\,\,\left\{ \matrix{ x = 3 + 2t \hfill \cr y = t \hfill \cr z = 1 - t \hfill \cr} \right.\) và d’ là giao tuyến của hai mặt phẳng \(\left( P \right):\,\,3y - z - 7 = 0\) ; \(\left( Q \right):\,\,3x + 3y - 2z - 17 = 0\). Khẳng định nào sau đây đúng?
Đáp án: A Phương pháp giải: Xác định phương trình giao tuyến của (P) và (Q). Chỉ ra 1 VTCP của \(\Delta \) và d. Kiểm tra xem 2 VTCP đó có quan hệ gì (cùng phương, vuông góc, …) Xét hệ phương trình để tìm giao điểm của hai đường thẳng. Lời giải chi tiết: Xét hệ phương trình \(\left\{ \matrix{ 3y - z - 7 = 0 \hfill \cr 3x + 3y - 2z - 17 = 0 \hfill \cr} \right. \Leftrightarrow \left\{ \matrix{ z = 3y - 7 \hfill \cr 3x + 3y - 6y + 14 - 17 = 0 \hfill \cr} \right. \Leftrightarrow \left\{ \matrix{ z = 3y - 7 \hfill \cr 3x - 3y - 3 = 0 \hfill \cr} \right. \Leftrightarrow \left\{ \matrix{ z = 3y - 7 \hfill \cr x = y + 1 \hfill \cr} \right.\) Đặt \(y = t' \Rightarrow x = t' + 1;\,\,z = 3t' - 7 \Rightarrow d':\,\,\left\{\begin{array}{l}x = 1 + t'\\y = t'\\z = - 7 + 3t'\end{array} \right.\) Ta có: \({\overrightarrow u _d} = \left( {2;1; - 1} \right);\,\,{\overrightarrow u _{d'}} = \left( {1;1;3} \right) \Rightarrow {\overrightarrow u _d}.{\overrightarrow u _{d'}} = 0 \Rightarrow d \bot d'.\) Xét hệ phương trình \(\left\{ \matrix{ 3 + 2t = 1 + t'\,\,\,\,\,\,\,\,\left( 1 \right) \hfill \cr t = t'\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left( 2 \right) \hfill \cr 1 - t = - 7 + 3t'\,\,\,\,\,\left( 3 \right) \hfill \cr} \right.\), từ (1) và (2) \( \Rightarrow t = t' = - 2\). Thay vào (3) ta có: \(1 + 2 = - 7 + 3.\left( { - 2} \right) \Leftrightarrow 3 = - 13\) (vô lí), do đó d và d’ chéo nhau. Chọn A. Câu hỏi 5 : Trong không gian với hệ tọa độ Oxyz, cho ba mặt phẳng \(\left( \alpha \right):\,\,2x - 4y + 6z - 1 = 0\) , \(\left( \beta \right):\,\,x + 3y - 2z + 6 = 0;\,\,\left( \gamma \right):\,\,x - 3y - 8z + 3 = 0\). Gọi d1 là giao tuyến của hai mặt phẳng \(\left( \alpha \right)\) và \(\left( \beta \right)\), d2 là giao tuyến của hai mặt phẳng \(\left( \beta \right)\) và \(\left( \gamma \right)\), d3 là giao tuyến của hai mặt phẳng \(\left( \alpha \right)\) và \(\left( \gamma \right)\). Khẳng định nào dưới đây là đúng ?
Đáp án: A Phương pháp giải: Tìm phương trình các đường thẳng d1, d2 và d3. Nhận xét các vector chỉ phương của d1, d2 và d3 không cùng phương. Tính \(\left[ {\overrightarrow {{u_1}} ;\overrightarrow {{u_2}} } \right].\overrightarrow {AB} \) với \(\overrightarrow {{u_1}} ;\overrightarrow {{u_2}} \) là VTCP của d1 và d2, \(A \in {d_1};B \in {d_2}\). - Nếu \(\left[ {\overrightarrow {{u_1}} ;\overrightarrow {{u_2}} } \right].\overrightarrow {AB} \ne 0 \Rightarrow {d_1},{d_2}\) chéo nhau thì loại đáp án A và C. - Nếu \(\left[ {\overrightarrow {{u_1}} ;\overrightarrow {{u_2}} } \right].\overrightarrow {AB} = 0 \Rightarrow {d_1},{d_2}\) cắt nhau thì loại đáp án B. Khi đó tìm \(M = {d_1} \cap {d_2}\) và thay tạo độ điểm M vào phương trình d3. Nếu \(M \in {d_3} \Rightarrow \) d1, d2 và d3 đồng quy. Lời giải chi tiết: Xét hệ phương trình \(\eqalign{ & \left\{ \matrix{ 2x - 4y + 6z - 1 = 0 \hfill \cr x + 3y - 2z + 6 = 0 \hfill \cr} \right. \Leftrightarrow \left\{ \matrix{ 2x - 4y + 6z - 1 = 0 \hfill \cr 3x + 9y - 6z + 18 = 0 \hfill \cr} \right. \Leftrightarrow \left\{ \matrix{ 5x + 5y + 17 = 0 \hfill \cr 2x - 4y + 6z - 1 = 0 \hfill \cr} \right. \cr & \Leftrightarrow \left\{ \matrix{ x = - y - {{17} \over 5} \hfill \cr - 2y - {{34} \over 5} - 4y + 6z - 1 = 0 \hfill \cr} \right. \Leftrightarrow \left\{ \matrix{ x = - y - {{17} \over 5} \hfill \cr - 6y + 6z - {{39} \over 5} = 0 \hfill \cr} \right. \Rightarrow \left\{ \matrix{ x = - y - {{17} \over 5} \hfill \cr z = y + {{39} \over {30}} \hfill \cr} \right. \cr} \) Đặt \(y = t \Rightarrow \left\{ \matrix{ x = - {{17} \over 5} - t \hfill \cr y = t \hfill \cr z = {{39} \over {30}} + t \hfill \cr} \right.\) là phương trình đường thẳng d1. Tương tự như vậy ta tìm được phương trình đường thẳng d2là : \(\left\{ \begin{array}{l}x = - \frac{9}{2} + 5t'\\y = - \frac{1}{2} - t'\\z = t'\end{array} \right.\) và phương trình đường thẳng \({d_3}:\,\,\left\{ \begin{array}{l}x = \frac{{15}}{2} - 25t''\\y = \frac{7}{2} - 11t''\\z = t''\end{array} \right.\) Ta có \(\overrightarrow {{u_1}} = \left( { - 1;1;1} \right);\,\,\overrightarrow {{u_2}} = \left( {5; - 1;1} \right);\,\,\overrightarrow {{u_3}} = \left( { - 25; - 11;1} \right)\) không cùng phương nên loại đáp án D. Lấy \(A\left( { - {{17} \over 5};0;{{39} \over {30}}} \right) \in {d_1},\,\,B\left( {{{ - 9} \over 2}; - {1 \over 2};0} \right),\,\,C\left( {{{15} \over 2};{7 \over 2};0} \right) \in {d_3}\) Xét \(\left[ {\overrightarrow {{u_1}} ;\overrightarrow {{u_2}} } \right] = \left( {2;6; - 4} \right);\,\,\overrightarrow {AB} = \left( { - {{11} \over {10}}; - {1 \over 2}; - {{39} \over {30}}} \right) \Rightarrow \left[ {\overrightarrow {{u_1}} ;\overrightarrow {{u_2}} } \right].\overrightarrow {AB} = 0 \Rightarrow {d_1};{d_2}\) cắt nhau \( \Rightarrow \) Loại đáp án B. Xét hệ phương trình : \(\left\{ \begin{array}{l}- \frac{{17}}{5} - t = - \frac{9}{2} + 5t'\\t = - \frac{1}{2} - t'\\\frac{{39}}{{30}} + t = t'\end{array} \right. \Rightarrow \left\{ \begin{array}{l}t = \frac{{ - 9}}{{10}}\\t' = \frac{2}{5}\end{array} \right. \Rightarrow M\left( { - \frac{5}{2}; -\frac{9}{{10}};\frac{2}{5}} \right)\) là giao điểm của d1 và d2.
Thay tạo độ điểm M vào phương trình đường thẳng d3 ta có : \({d_3}:\,\,\left\{ \begin{array}{l}- \frac{5}{2} = \frac{{15}}{2} - 25t''\\- \frac{9}{{10}} = \frac{7}{2} - 11t''\\\frac{2}{5} = t''\end{array} \right. \Rightarrow t'' = \frac{2}{5} \Rightarrow M \in{d_3}\) Vậy ba đường thẳng d1, d2 và d3 đồng quy tại \(M\left( { - {5 \over 2}; - {9 \over {10}};{2 \over 5}} \right)\). Chọn A. Câu hỏi 6 : Trong không gian với hệ tọa độ \(Oxyz,\) cho điểm \(A\left( 1;1;1 \right)\) và đường thẳng \(d:\frac{x-1}{1}=\frac{y}{-\,2}=\frac{z-1}{9}.\) Biết đường thẳng \(\Delta \) qua \(A,\) cắt \(d\) và khoảng cách từ gốc tọa độ đến \(\Delta \) nhỏ nhất, \(\Delta \) có một vectơ chỉ phương là \(\left( 1;a;b \right).\) Tổng \(a+b\) là
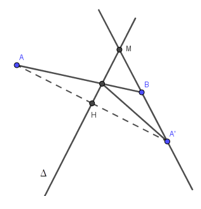
Đáp án: A Phương pháp giải: Dựng hình, đưa về bài toán tìm điểm để khoảng cách từ một điểm đến một mặt phẳng nhỏ nhất Lời giải chi tiết: Đường thẳng \(d\) đi qua \(B\left( 1;0;1 \right),\) có vectơ chỉ phương \(\vec{u}=\left( 1;-\,2;9 \right)\)\(\Rightarrow \,\,\left[ \overrightarrow{AB};\vec{u} \right]=\left( 9;0;-\,1 \right).\) Phương trình mặt phẳng \(\left( \alpha \right)\) chứa \(d\) và đi qua \(A\) là \(\left( \alpha \right):9x-z-8=0.\) Gọi \(I\) là hình chiếu của \(O\) trên \(\Delta ,\) \(H\) là hình chiếu của \(O\) trên \(\left( \alpha \right).\) Ta có \(d\left( O;\left( \Delta \right) \right)=OI\le OH\Rightarrow \,\,{{d}_{\min }}=OH\)\(\Leftrightarrow \)\(H\) là hình chiếu của \(O\) trên \(\left( \alpha \right).\) Phương trình đường thẳng \(OH\) là \(\left\{ \begin{align} x=9t \\ y=0 \\ z=-\,t \\ \end{align} \right.\)\(\Rightarrow \,\,H\left( 9t;0;-\,t \right)\in \left( \alpha \right)\)\(\Rightarrow t=\frac{4}{41}.\) Vậy \(H\left( \frac{36}{41};0;-\,\frac{4}{41} \right)\Rightarrow \overrightarrow{HA}=\left( \frac{5}{41};1;\frac{45}{41} \right)=\frac{5}{41}\left( 1;\frac{41}{5};9 \right)\Rightarrow \left\{\begin{align} a=\frac{41}{5} \\ b=9 \\ \end{align} \right..\) \(\Rightarrow a+b=\frac{41}{5}+9=\frac{86}{5}.\) Chọn A Câu hỏi 7 : Trong không gian với hệ tọa độ \(Oxyz,\) cho hai điểm \(A\left( -\,1;2;1 \right),\,\,B\left( 1;2;-\,3 \right)\) và đường thẳng \(d:\frac{x+1}{2}=\frac{y-5}{2}=\frac{z}{-\,1}.\) Tìm vectơ chỉ phương \(\vec{u}\) của đường thẳng \(\Delta \) đi qua \(A\) và vuông góc với \(d\) đồng thời cách \(B\) một khoảng lớn nhất.
Đáp án: A Phương pháp giải: Lời giải chi tiết: Câu hỏi 8 : Trong không gian với hệ tọa độ \(Oxyz\), cho mặt phẳng \((P):x+y-4z=0\), đường thẳng \(d:\frac{x-1}{2}=\frac{y+1}{-1}=\frac{z-3}{1}\) và điểm \(A(1;3;1)\)thuộc mặt phẳng \((P)\). Gọi \(\Delta \) là đường thẳng đi qua A, nằm trong mặt phẳng (P) và cách d một khoảng cách lớn nhất. Gọi \(\overrightarrow{u}=(a;b;1)\) là một VTCP của đường thẳng \(\Delta \). Tính \(a+2b\).
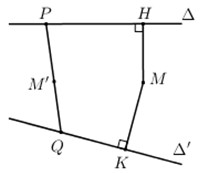
Đáp án: A Phương pháp giải: Đánh giá, tìm vị trí của \(\Delta \)để khoảng cách giữa 2 đường thẳng là lớn nhất. Lời giải chi tiết: Kẻ AH vuông góc d, qua A kẻ d’ // d. Dựng mặt phẳng (Q) chứa d’ và vuông góc AH, (Q) cắt (P) tại \({{\Delta }_{o}}\). Ta sẽ chứng minh \({{\Delta }_{0}}\) thỏa mãn yêu cầu đề bài (cách d một khoảng cách lớn nhất). Vì \(\left\{ \begin{align} AH\bot d \\ AH\bot (Q) \\ \end{align} \right.\Rightarrow d//(Q)\Rightarrow d\left( d;\left( Q \right) \right)=AH=d\left( d;{{\Delta }_{0}} \right),\,\,(do\,\,{{\Delta }_{0}}\subset (Q))\) Lấy \(\Delta \)là đường thẳng bất kì qua A và nằm trong (P). Gọi \((Q')\)là mặt phẳng chứa d’ và \(\Delta \Rightarrow d//(Q')\)\(\Rightarrow d(d;(Q'))=d(H;(Q'))\) Kẻ \(HA'\bot (Q'),\,\,A'\in (Q')\Rightarrow d(d;(Q'))=HA'=d(d;\Delta )\). Ta có: \(HA'\le HA\Rightarrow \) Khoảng cách từ d đến\(\Delta \) lớn nhất bằng AH khi \(\Delta \) trùng \({{\Delta }_{o}}\). *) Tìm tọa độ điểm H: Gọi \(\left( \alpha \right)\): mặt phẳng qua A vuông góc d \(\Rightarrow \left( \alpha \right):\,2.(x-1)-1(y-3)+1(z-1)=0\Leftrightarrow 2x-y+z=0\) \(\begin{array}{l}H = d \cap \left( \alpha \right) \Rightarrow \frac{{x - 1}}{2} = \frac{{y + 1}}{{ - 1}} = \frac{{z - 3}}{1} = \frac{{2x - 2 - y - 1 + z - 3}}{{4 + 1 + 1}} = \frac{{2x - y + z - 6}}{6} = \frac{{0 - 6}}{6} = - 1\\ \Rightarrow \left\{ \begin{array}{l}x = - 1\\y = 0\\z = 2\end{array} \right. \Rightarrow H( - 1;0;2)\end{array}\) \(\Rightarrow \overrightarrow{AH}\left( -2;-3;1 \right)\) \({{\Delta }_{o}}\) có 1 VTCP : \(\overrightarrow{u}=\left[ \overrightarrow{AH};\overrightarrow{{{n}_{(P)}}} \right],\,\,\)với \(\left( \overrightarrow{{{n}_{(P)}}}=(1;1;-4) \right)\) \(\Rightarrow \overrightarrow{u}=(11;-7;1)\Rightarrow a=11;\,b=-7\Rightarrow a+2b=-3\) Chọn: A Câu hỏi 9 : Trong không gian Oxyz cho mặt phẳng \(\left( Q \right):\,\,x + 2y + z - 3 = 0\) và đường thẳng \(d:\,\,{{x + 1} \over 1} = {{y - 2} \over { - 1}} = {{z + 3} \over { - 1}}\). Viết phương trình mp(P) chứa (d) và hợp với mặt phẳng (Q) một góc \(\alpha \) thỏa mãn \(\cos \alpha = {{\sqrt 3 } \over 6}\).
Đáp án: A Phương pháp giải: Gọi \(\overrightarrow n = \left( {a;b;c} \right)\) là 1 VTPT của mặt phẳng (P), \(d \subset \left( P \right) \Rightarrow \overrightarrow n \bot \overrightarrow {{u_d}} \) \(\cos \alpha = \left| {\cos \left( {{{\overrightarrow n }_{\left( Q \right)}};\overrightarrow n } \right)} \right| = {{\left| {{{\overrightarrow n }_{\left( Q \right)}}.\overrightarrow n } \right|} \over {\left| {{{\overrightarrow n }_{\left( Q \right)}}} \right|.\left| {\overrightarrow n } \right|}}\) Lời giải chi tiết: Gọi \(\overrightarrow n = \left( {a;b;c} \right)\) là 1 VTPT của mặt phẳng (P), \(\overrightarrow u = \left( {1; - 1; - 1} \right)\) là 1 VTCP của đường thẳng d. \(d \subset \left( P \right) \Rightarrow \overrightarrow n \bot \overrightarrow u \Rightarrow a - b - c = 0 \Leftrightarrow a = b + c\) \(\eqalign{ & \cos \alpha = \left| {\cos \left( {{{\overrightarrow n }_{\left( Q \right)}};\overrightarrow n } \right)} \right| = {{\left| {{{\overrightarrow n }_{\left( Q \right)}}.\overrightarrow n } \right|} \over {\left| {{{\overrightarrow n }_{\left( Q \right)}}} \right|.\left| {\overrightarrow n } \right|}} \cr & \Leftrightarrow {{\sqrt 3 } \over 6} = {{\left| {a + 2b + c} \right|} \over {\sqrt 6 .\sqrt {{a^2} + {b^2} + {c^2}} }} \cr & \Leftrightarrow {a^2} + {b^2} + {c^2} = 2{\left( {a + 2b + c} \right)^2} \cr & \Leftrightarrow {\left( {b + c} \right)^2} + {b^2} + {c^2} = 2{\left( {3b + 2c} \right)^2} \cr & \Leftrightarrow 2{b^2} + 2bc + 2{c^2} = 18{b^2} + 8{c^2} + 24bc \cr & \Leftrightarrow 16{b^2} + 22bc + 6{c^2} = 0 \cr & \Leftrightarrow \left[ \matrix{ b = - {3 \over 8}c \hfill \cr b = - c \hfill \cr} \right. \cr} \) TH1 : \(b = - c \Rightarrow a = 0 \Rightarrow \overrightarrow n = \left( {0; - c;c} \right) = c\left( {0; - 1;1} \right) \Rightarrow \left( {0; - 1;1} \right)\) cũng là 1 VTPT của (P), dựa vào các đáp án ta thấy không có đáp án nào thỏa mãn. TH2 : \(b = - {3 \over 8}c \Rightarrow a = {5 \over 8}c \Rightarrow \overrightarrow n = \left( {{5 \over 8}c; - {3 \over 8}c;c} \right) = - {c \over 8}\left( { - 5;3; - 8} \right) \Rightarrow \left( { - 5;3; - 8} \right)\) cũng là 1 VTPT của (P). Lấy \(A\left( { - 1;2; - 3} \right) \in d \Rightarrow A \in \left( P \right) \Rightarrow \) Phương trình mặt phẳng (P) là \( - 5\left( {x + 1} \right) + 3\left( {y - 2} \right) - 8\left( {z + 3} \right) = 0 \Leftrightarrow - 5x + 3y - 8z - 35 = 0\) Chọn A. Câu hỏi 10 : Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng \(\left( P \right):\,\,\left( {{m^2} + m + 1} \right)x + 2\left( {{m^2} - 1} \right)y + 2\left( {m + 2} \right)z + {m^2} + m + 1 = 0\) luôn chứa đường thẳng \(\Delta \) cố định khi \(m\) thay đổi. Tính khoảng cách từ gốc tọa độ đến \(\Delta \).
Đáp án: D Phương pháp giải: +) Đưa phương trình về dạng phương trình bậc hai ẩn \(m\) . Tìm điều kiện để phương trình ẩn \(m\) nghiệm đúng với mọi \(x;y;z\). Suy ra phương trình đường thẳng \(\Delta \). +) Sử dụng công thức tính khoảng cách từ 1 điểm M đến một đường thẳng d: \(d\left( {M;d} \right) = \frac{{\left| {\left[ {\overrightarrow {M{M_0}} ;{{\overrightarrow u }_d}} \right]} \right|}}{{\left| {\overrightarrow {{u_d}} } \right|}}\,\,\,\left( {{M_0} \in d} \right)\) Lời giải chi tiết: Ta có: \(\left( P \right):\,\,\left( {{m^2} + m + 1} \right)x + 2\left( {{m^2} - 1} \right)y + 2\left( {m + 2} \right)z + {m^2} + m + 1 = 0\) \( \Leftrightarrow \left( {x + 2y + 2z + 1} \right){m^2} + \left( {x + 2z + 1} \right)m + x - 2y + 4z + 1 = 0\) Phương trình nghiệm đung với mọi \(m \Leftrightarrow \left\{ \begin{array}{l}x + 2y + 1 = 0\\x + 2z + 1 = 0\\x - 2y + 4z + 1 = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = - 1 - 2t\\y = t\\z = t\end{array} \right.\) Vậy \(\left( P \right)\) luôn chứa đường thẳng cố định \(\Delta :\,\,\left\{ \begin{array}{l}x = - 1 - 2t\\y = t\\z = t\end{array} \right.\). \({\overrightarrow u _\Delta } = \left( { - 2;1;1} \right)\) là 1 VTCP của đường thẳng \(\Delta \), \(M\left( { - 1;0;0} \right) \in \Delta \). \( \Rightarrow \left[ {\overrightarrow {OM} ;\overrightarrow {{u_\Delta }} } \right] = \left( {0;1; - 1} \right)\) Khi đó ta có \(d\left( {O;\Delta } \right) = \frac{{\left| {\left[ {\overrightarrow {OM} ;\overrightarrow {{u_\Delta }} } \right]} \right|}}{{\left| {\overrightarrow {{u_\Delta }} } \right|}} = \frac{{\sqrt 2 }}{{\sqrt 6 }} = \frac{1}{{\sqrt 3 }}\) Chọn D. Câu hỏi 11 : Trong không gian Oxyz, cho hai điểm \(A(0; - 1;2),\,\,B(1;1;2)\) và đường thẳng \(d:\,\,\frac{{x + 1}}{1} = \frac{y}{1} = \frac{{z - 1}}{1}\). Biết điểm M(a;b;c) thuộc đường thẳng d sao cho tam giác MAB có diện tích nhỏ nhất. Khi đó, giá trị \(T = a + 2b + 3c\) bằng
Đáp án: A Phương pháp giải: Do A, B cố định nên, tam giác MAB có diện tích nhỏ nhất khi và chỉ khi khoảng cách từ M đến đường thẳng AB là nhỏ nhất. Mà M thuộc d nên khoảng cách \(d{(M;AB)_{\min }} = d(d;AB) = \) Độ dài đoạn vuông góc chung của d và AB. Lời giải chi tiết: \(A(0; - 1;2),\,\,B(1;1;2) \Rightarrow \overrightarrow {AB} \left( {1;2;0} \right) \Rightarrow AB:\left\{ \begin{array}{l}x = {t_1}\\y = - 1 + 2{t_1}\\z = 2\end{array} \right.\) \(\left( d \right):\,\,\frac{{x + 1}}{1} = \frac{y}{1} = \frac{{z - 1}}{1} \Leftrightarrow \left( d \right):\left\{ \begin{array}{l}x = - 1 + t\\y = t\\z = 1 + t\end{array} \right.\) Mà M thuộc d nên khoảng cách \(d{(M;AB)_{\min }} = d(d;AB) = \) Độ dài đoạn vuông góc chung của d và AB. Gọi HK là đoạn vuông góc chung của AB và d \(\left( {H \in d,\,\,K \in AB} \right)\) Vì \(H \in d,\,\,K \in AB\) nên, giả sử \(H\left( { - 1 + t;\,\,\,t\,\,;1 + t} \right),\,K\left( {{t_1}; - 1 + 2{t_1};2} \right) \Rightarrow \overrightarrow {HK} = \left( {{t_1} - t + 1;2{t_1} - t - 1;1 - t} \right)\) HK là đoạn vuông góc chung của AB và d\( \Rightarrow \left\{ \begin{array}{l}\overrightarrow {HK} \bot \overrightarrow {{u_{AB}}} \\\overrightarrow {HK} \bot \overrightarrow {{u_d}} \end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}\left( {{t_1} - t + 1} \right).1 + \left( {2{t_1} - t - 1} \right).2 + \left( {1 - t} \right)0 = 0\\\left( {{t_1} - t + 1} \right).1 + \left( {2{t_1} - t - 1} \right).1 + \left( {1 - t} \right).1 = 0\end{array} \right.\) \( \Leftrightarrow \left\{ \begin{array}{l}5{t_1} - 3t = 1\\3{t_1} - 3t = - 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{t_1} = 1\\t = \frac{4}{3}\end{array} \right. \Rightarrow H\left( {\frac{1}{3};\frac{4}{3};\frac{7}{3}} \right)\) Diện tích tam giác MAB nhỏ nhất khi M(a;b;c) trùng\(H\left( {\frac{1}{3};\frac{4}{3};\frac{7}{3}} \right)\). \( \Rightarrow a = \frac{1}{3},\,b = \frac{4}{3},\,c = \frac{7}{3} \Rightarrow T = \frac{1}{3} + 2.\frac{4}{3} + 3.\frac{7}{3} = 10\) Chọn: A Câu hỏi 12 : Trong không gian Oxyz, cho đường thẳng \(\Delta :\frac{x}{1} = \frac{{y - 1}}{1} = \frac{z}{1}\) và hai điểm \(A(1;2; - 5),\,B( - 1;0;2)\). Biết điểm M thuộc \(\Delta \) sao cho biểu thức \(T = \left| {MA - MB} \right|\) đạt GTLN là \({T_{max}}\). Khi đó, \({T_{max}}\) bằng bao nhiêu?
Đáp án: C Phương pháp giải: Lời giải chi tiết: +) Chứng minh A, B, \(\Delta \) đồng phẳng: Gọi \(\left( \alpha \right)\) là mặt phẳng qua A và chứa \(\Delta \) (\(\Delta \) đi qua \(C(0;1;0)\) và nhận \(\overrightarrow u (1;1;1)\) là VTCP) \(\overrightarrow {AC} = \left( { - 1; - 1;5} \right)\) \(\left( \alpha \right)\) có 1 VTPT \(\overrightarrow n = \left[ {\overrightarrow u ;\overrightarrow {AC} } \right] = (6; - 6;0)\). Phương trình mặt phẳng \(\left( \alpha \right)\): \(6(x - 1) - 6(y - 2) + 0(z + 5) = 0 \Leftrightarrow x - y + 1 = 0\) Ta có: \(\,B( - 1;0;2);\,\,\, - 1 + 0 + 1 = 0 \Rightarrow B \in \left( \alpha \right)\) \( \Rightarrow \) A, B, \(\Delta \) đồng phẳng. +) Tìm giao điểm của M của AB và \(\Delta \): \(\Delta :\frac{x}{1} = \frac{{y - 1}}{1} = \frac{z}{1}\) có PTTS : \(\left\{ \begin{array}{l}x = t\\y = 1 + t\\z = t\end{array} \right.\) , \(M \in \Delta \Rightarrow M(t;1 + t;t)\) \(\,\overrightarrow {AB} ( - 2; - 2;7)\), \(\overrightarrow {AM} \left( {t - 1;t - 1;t + 5} \right)\) \(A,M,B\) thẳng hàng \( \Rightarrow \overrightarrow {AM} //\overrightarrow {AB} \Rightarrow \frac{{t - 1}}{{ - 2}} = \frac{{t - 1}}{{ - 2}} = \frac{{t + 5}}{7} \Leftrightarrow t = - \frac{1}{3} \Rightarrow M\left( {\frac{{ - 1}}{3};\frac{2}{3}; - \frac{1}{3}} \right)\) Mặt khác, \(\overrightarrow {AM} \left( { - \frac{4}{3}; - \frac{4}{3};\frac{{14}}{3}} \right);\,\,\overrightarrow {BM} \left( {\frac{2}{3};\frac{2}{3};\frac{{ - 7}}{3}} \right) \Rightarrow \overrightarrow {AM} = - 2\overrightarrow {BM} \Rightarrow \) M nằm giữa A và B, suy ra, trong \(\left( \alpha \right)\), A và B nằm khác phía so với đường thẳng \(\Delta \). Gọi A’ là điểm đối xứng với A qua B. Khi đó, \(\left| {MA - MB} \right| = \left| {MA' - MB} \right| \le A'B\), \({\left| {MA' - MB} \right|_{max}} = A'B\) khi và chỉ khi M là giao điểm của A’B và đường thẳng \(\Delta \) (điểm M như trên là tồn tại). +) Tìm tọa độ điểm A’: Gọi \(\left( \beta \right)\) là mặt phẳng qua A và vuông góc \(\Delta \), khi đó, \(\left( \beta \right)\) nhận \(\overrightarrow {{u_\Delta }} (1;1;1)\) là 1 VTPT. Phương trình mặt phẳng \(\left( \beta \right)\): \(1.(x - 1) + 1.(y - 2) + 1.(z + 5) = 0 \Leftrightarrow x + y + z + 2 = 0\) \(H \in \Delta \Rightarrow \)Gọi \(H(m;1 + m;m)\) \(H \in \left( \beta \right) \Rightarrow m + 1 + m + m + 2 = 0 \Leftrightarrow m = - 1\) \( \Rightarrow H( - 1;0; - 1)\) H là trung điểm của AA’ \( \Rightarrow \left\{ \begin{array}{l}{x_H} = \frac{{{x_A} + {x_{A'}}}}{2}\\{y_H} = \frac{{{y_A} + {y_{A'}}}}{2}\\{z_H} = \frac{{{z_A} + {z_{A'}}}}{2}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{x_{A'}} = - 3\\{y_{A'}} = - 2\\{z_{A'}} = 3\end{array} \right.\) Độ dài đoạn A’B: \(A'B = \sqrt {{{( - 1 + 3)}^2} + {{(0 + 2)}^2} + {{(2 - 3)}^2}} = 3\) Vậy, \({T_{max}} = 3\) Chọn: C Câu hỏi 13 : Trong không gian với hệ tọa độ \(Oxyz,\) cho tam giác \(ABC\) có \(A\left( 2;3;3 \right)\), phương trình đường trung tuyến kẻ từ B là \(\frac{x-3}{-1}=\frac{y-3}{2}=\frac{z-2}{-1}\), phương trình đường phân giác trong của góc \(C\) là \(\frac{{x - 2}}{2} = \frac{{y - 4}}{{ - 1}} = \frac{{z - 2}}{{ - 1}}.\) Biết rằng \(\overrightarrow{u}=\left( m;n;-1 \right)\) là một véc tơ chỉ phương của đường thẳng \(AB.\) Tính giá trị của biểu thức \(T={{m}^{2}}+{{n}^{2}}.\)
Đáp án: A Phương pháp giải: Dựa vào tính chất đường phân giác để tìm điểm đối xứng qua đường thẳng Lời giải chi tiết: Kí hiệu 2 đường thẳng trung tuyến và phân giác lần lượt là \({{d}_{1}},\,\,{{d}_{2}}.\) Gọi \(M\) là trung điểm của \(AC \Rightarrow \,\,M \in \left( {{d_1}} \right) \Rightarrow \,\,M\left( { - \,t + 3;2t + 3; - \,t + 2} \right)\) Suy ra \(C\left( -\,2t+4;4t+3;-\,2t+1 \right)\) mà \(C\in \left( {{d}_{2}} \right)\,\,\xrightarrow{{}}\,\,t=0\Rightarrow \,\,C\left( 4;3;1 \right).\) Phương trình mặt phẳng \(\left( P \right)\) qua \(A,\) vuông góc với \({{d}_{2}}\) là \(2x-y-z+2=0.\) Gọi \(N\) là điểm đối xứng của \(A\) qua \(\left( {{d}_{2}} \right)\Rightarrow \,\,N\in BC\) và \(N\in \left( P \right).\) Gọi \(E\) là trung điểm của \(AN\Rightarrow \,\,\)\(E\) là giao điểm của \({{d}_{2}}\) và \(\left( P \right)\)\(\Rightarrow \,\,E\left( 2;4;2 \right).\) Suy ra \(N\left( 2;5;1 \right)\)\(\Rightarrow \,\,AC=NC\Rightarrow \,\,N\) trùng \(B.\) Vậy \(\left\{ \begin{array}{l}A\left( {2;3;3} \right)\\B\left( {2;4;2} \right)\end{array} \right. \Rightarrow \overrightarrow {AB} = \left( {0;1; - 1} \right).\) Chọn A Câu hỏi 14 : Trong không gian với hệ tọa độ Oxyz, cho đường thẳng d và mặt cầu (S) lần lượt có phương trình là: \(d:\frac{x+3}{-1}=\frac{y}{2}=\frac{z+1}{2};\left( S \right):{{x}^{2}}+{{y}^{2}}+{{z}^{2}}-2x+4y+2z-18=0\) Biết d cắt (S) tại hai điểmM, N thì độ dài đoạn MN là:
Đáp án: B Phương pháp giải: Lời giải chi tiết: Câu hỏi 15 : Trong không gian với hệ tọa độ Oxyz, cho đường thẳng \(\left( \Delta \right):\,\,\frac{{x + 1}}{3} = \frac{{y - 4}}{{ - 2}} = \frac{{z - 4}}{{ - 1}}\) và các điểm \(A\left( {2;3; - 4} \right);\,\,B\left( {4;6; - 9} \right).\) Gọi C, D là các điểm thay đổi trên \(\Delta \) sao cho \(CD = \sqrt {14} \) và mặt cầu nội tiếp tứ diện ABCD có thể tích lớn nhất. Khi đó tọa độ trung điểm CD là:
Đáp án: B Phương pháp giải: Lời giải chi tiết:
Gọi I, r theo thứ tự là tâm và bán kính mặt cầu nội tiếp tứ diện ABCD. Ta có \(r = d\left( {I;\left( {IAB} \right)} \right) = d\left( {I;\left( {IBC} \right)} \right) = d\left( {I;\left( {ICD} \right)} \right) = d\left( {I;\left( {IDA} \right)} \right)\) I nằm trong tứ diện \(ABCD \Rightarrow {V_{ABCD}} = {V_{IABC}} + {V_{IBCD}} + {V_{ICDA}} + {V_{IBDA}}\) \(\begin{array}{l} \Rightarrow {V_{ABCD}} = \frac{1}{3}r.{S_{ABC}} + \frac{1}{3}r.{S_{BCD}} + \frac{1}{3}r.{S_{CDA}} + \frac{1}{3}r.{S_{BDA}}\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = \frac{1}{3}r\left( {{S_{ABC}} + {S_{BCD}} + {S_{CDA}} + {S_{BDA}}} \right)\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = \frac{1}{3}r.{S_{tp}}\\ \Rightarrow r = \frac{{3{V_{ABCD}}}}{{{S_{tp}}}}\end{array}\) \({V_{ABCD}} = \frac{1}{6}AB.CD.d\left( {AB;CD} \right) = const\) vì AB, \(\Delta \) cố định và \(CD = \sqrt {14} \). \({S_{BCD}} = \frac{1}{2}CD.d\left( {B;\Delta } \right) = const\) \({S_{ABC}};\,\,{S_{BDA}}\) thay đổi vì C, D thay đổi trên \(\Delta \) \( \Rightarrow {r_{\max }} \Leftrightarrow {S_{tp\,\min }} \Leftrightarrow {\left( {{S_{ABC}} + {S_{BDA}}} \right)_{\min }}\) Vì \(C;D \in \Delta \Rightarrow C\left( { - 1 + 3t;4 - 2t;4 - t} \right);\,\,D\left( { - 1 + 3t';4 - 2t';4 - t'} \right)\) (giả sử \(t' > 1\)) \(CD = \sqrt {14} \Leftrightarrow \sqrt {14{{\left( {t' - t} \right)}^2}} = \sqrt {14} \Leftrightarrow \left| {t' - t} \right| = 1 \Leftrightarrow t' = 1 + t\) \(\begin{array}{l}{S_{ABC}} = \frac{1}{2}\left| {\left[ {\overrightarrow {AB} ;\overrightarrow {AC} } \right]} \right| = \frac{1}{2}\sqrt {{{\left( {13t - 29} \right)}^2} + {{\left( {13t + 1} \right)}^2} + {{\left( {13t - 11} \right)}^2}} \\{S_{BDA}} = \frac{1}{2}\left| {\left[ {\overrightarrow {AB} ;\overrightarrow {AD} } \right]} \right| = \frac{1}{2}\sqrt {{{\left( {13t' - 29} \right)}^2} + {{\left( {13t' + 1} \right)}^2} + {{\left( {13t' - 11} \right)}^2}} \\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = \frac{1}{2}\sqrt {{{\left( {13t - 16} \right)}^2} + {{\left( {13t + 14} \right)}^2} + {{\left( {13t + 2} \right)}^2}} \end{array}\) \(\begin{array}{l} \Rightarrow {S_{ABC}} + {S_{BDA}}\\ = \frac{1}{2}\left[ {\sqrt {{{\left( {13t - 29} \right)}^2} + {{\left( {13t + 1} \right)}^2} + {{\left( {13t - 11} \right)}^2}} + \sqrt {{{\left( {13t - 16} \right)}^2} + {{\left( {13t + 14} \right)}^2} + {{\left( {13t + 2} \right)}^2}} } \right]\\ = \frac{1}{2}\left[ {\sqrt {{{\left( {a - 29} \right)}^2} + {{\left( {a + 1} \right)}^2} + {{\left( {a - 11} \right)}^2}} + \sqrt {{{\left( {a - 16} \right)}^2} + {{\left( {a + 14} \right)}^2} + {{\left( {a + 2} \right)}^2}} } \right]\,\,\,\left( {a = 13t} \right)\\ = \frac{1}{2}\left[ {\sqrt {3{a^2} - 78a + 963} + \sqrt {3{a^2} + 456} } \right]\\ = \frac{{\sqrt 3 }}{2}\left[ {\sqrt {{a^2} - 26a + 321} + \sqrt {{a^2} + 152} } \right]\\ = \frac{{\sqrt 3 }}{2}\left[ {\sqrt {{{\left( {a - 13} \right)}^2} + {{\left( {0 - \sqrt {152} } \right)}^2}} + \sqrt {{{\left( {a - 0} \right)}^2} + {{\left( {0 - \left( { - \sqrt {152} } \right)} \right)}^2}} } \right]\\ = \frac{{\sqrt 3 }}{2}\left( {MP + MQ} \right)\end{array}\) Với \(M\left( {a;0} \right);\,\,P\left( {13;\sqrt {152} } \right);\,\,Q\left( {0; - \sqrt {152} } \right)\) trong mặt phẳng Oxy. \( \ge \frac{{\sqrt 3 }}{2}PQ = \frac{{\sqrt {483} }}{2}\). Dấu bằng xảy ra \( \Leftrightarrow \) M, N, P thẳng hàng và M nằm giữa P và Q \( \Leftrightarrow \overrightarrow {PM} \) và \(\overrightarrow {PQ} \) cùng phương \( \Leftrightarrow a = \frac{{13}}{2} \Leftrightarrow t = \frac{1}{2}\). \( \Rightarrow C\left( {\frac{1}{2};3;\frac{7}{2}} \right);\,\,D\left( {\frac{7}{2};1;\frac{5}{2}} \right)\). Vậy \({\left( {{S_{ABC}} + {S_{BDA}}} \right)_{\min }} = \frac{{\sqrt {483} }}{2} \Leftrightarrow \) Trung điểm của CD là \(J\left( {2;2;3} \right)\). Chọn B. Câu hỏi 16 : Trong hệ tọa độ Oxyz cho hai điểm \(A\left( 1;5;0 \right);\,\,B\left( 3;3;6 \right)\) và đường thẳng \(\left( d \right):\,\,\left\{ \begin{array}{l}x = - 1 + 2t\\y = 1 - t\\z = 2t\end{array} \right..\) Một điểm M thay đổi trên d. Biết giá trị nhỏ nhất của nửa chu vi tam giác MAB là số có dạng \(\sqrt{a}+\sqrt{b}\) với a, b là các số nguyên. Khi đó:
Đáp án: A Phương pháp giải: +) Kiểm tra AB và d chéo nhau. +) \({{C}_{MAB\,\min }}\Leftrightarrow {{\left( MA+MB \right)}_{\min }}\Leftrightarrow MA=MB\) Lời giải chi tiết: Ta có \(\overrightarrow{AB}=\left( 2;-2;6 \right)\); \(\overrightarrow{{{u}_{d}}}=\left( 2;-1;2 \right)\) d đi qua điểm \(M\left( -1;1;0 \right)\) \(\Rightarrow \left[ \overrightarrow{AB}.\overrightarrow{{{u}_{d}}} \right].\overrightarrow{AM}\ne 0\Rightarrow AB\) và d chéo nhau. Ta có \({{C}_{MAB}}=MA+MB+AB\) Do AB không đổi nên \({{C}_{MAB\,\,\min }}\Leftrightarrow {{\left( MA+MB \right)}_{\min }}\) Do AB và d chéo nhau nên \(MA+MB\overset{Cauchy}{\mathop{\ge }}\,2\sqrt{MA.MB}\Leftrightarrow {{\left( MA+MB \right)}_{\min }}\Leftrightarrow MA=MB\) \(\Rightarrow M\in \) mặt phẳng trung trực của AB đi qua trung điểm \(I\left( 2;4;3 \right)\) của AB và nhận \(\left( 1;-1;3 \right)\) là 1 VTPT. \(\Rightarrow M\in \left( P \right):\,\,x-y+3z-7=0\) \(\Rightarrow M\in \left( d \right)\Rightarrow M\left( -1+2t;1-t;2t \right)\) Thay vào mặt phẳng (P) \(\Rightarrow -1+2t-1+t+6t-7=0\Leftrightarrow t=1\Rightarrow M\left( 1;0;2 \right)\Rightarrow MA=MB=\sqrt{29}\) \(AB=2\sqrt{11}\Rightarrow {{C}_{\Delta MAB}}=2\sqrt{11}+2\sqrt{29}\Rightarrow {{p}_{\Delta MAB}}=\sqrt{11}+\sqrt{29}\Rightarrow \left\{ \begin{align} & a=11 \\ & b=29 \\\end{align} \right.\Rightarrow a+b=40\) Chọn A. Câu hỏi 17 : Trong không gian Oxyz, cho đường thẳng \(d:\left\{ \begin{array}{l}x = 1 + 3t\\y = 1 + 4t\\z = 1\end{array} \right.\). Gọi \(\Delta \) là đường thẳng đi qua điểm \(A\left( {1;1;1} \right)\) và có vectơ chỉ phương \(\overrightarrow u = \left( {1; - 2;2} \right)\). Đường phân giác của góc nhọn tạo bởi d và \(\Delta \) có phương trình là
Đáp án: C Phương pháp giải: Phương pháp xác định đường phân giác của hai đường thẳng cắt nhau : Cho hai đường thẳng \({d_1},{d_2}\) có VTCP lần lượt là \(\overrightarrow {{u_1}} ,\overrightarrow {{u_2}} \) + Nếu \(\cos \left( {\overrightarrow {{u_1}} ,\overrightarrow {{u_2}} } \right) > 0\) thì VTCP của đường phân giác góc nhọn là \(\overrightarrow u = \left| {\overrightarrow {{u_2}} } \right|.\overrightarrow {{u_1}} + \left| {\overrightarrow {{u_1}} } \right|.\overrightarrow {{u_2}} \) + Nếu \(\cos \left( {\overrightarrow {{u_1}} ,\overrightarrow {{u_2}} } \right) < 0\) thì VTCP của đường phân giác góc nhọn là \(\overrightarrow u = \left| {\overrightarrow {{u_2}} } \right|.\overrightarrow {{u_1}} - \left| {\overrightarrow {{u_1}} } \right|.\overrightarrow {{u_2}} \) Lời giải chi tiết: Ta có : \(\overrightarrow {{u_\Delta }} = \left( {1; - 2;2} \right) \Rightarrow \left| {\overrightarrow {{u_\Delta }} } \right| = 3\) \(d\) có một VTCP là \(\overrightarrow {{u_d}} = \left( {3;4;0} \right) \Rightarrow \left| {\overrightarrow {{u_d}} } \right| = 5\) \(\cos \left( {\overrightarrow {{u_\Delta }} ,\overrightarrow {{u_d}} } \right) = \frac{{3 - 8}}{{3.5}} < 0 \Rightarrow \left( {\overrightarrow {{u_\Delta }} ,\overrightarrow {{u_d}} } \right)\) là góc tù. \(\overrightarrow {{v_1}} = 5.\overrightarrow {{u_\Delta }} = \left( {5; - 10;10} \right),\overrightarrow {{v_2}} = 3.\overrightarrow {{u_d}} = \left( {9;12;0} \right)\) Một VTCP của đường phân giác \(d'\) là \(\overrightarrow {{v_1}} - \overrightarrow {{v_2}} = \left( { - 4; - 22;10} \right)\) hay \(\overrightarrow u = \left( {2;11; - 5} \right)\) Phương trình \(d':\left\{ \begin{array}{l}x = 1 + 2t\\y = 1 + 11t\\z = 1 - 5t\end{array} \right.\) hay \(d':\left\{ \begin{array}{l}x = - 1 + 2t\\y = - 10 + 11t\\z = 6 - 5t\end{array} \right.\) Chọn C. Câu hỏi 18 : Trong không gian Oxyz, cho đường thẳng d : \(\left\{ \begin{array}{l}x = 1 + 3t\\y = - 3\\z = 5 + 4t\end{array} \right..\) Gọi \(\Delta \) là đường thẳng đi qua điểm \(A\left( {1; - 3;5} \right)\) và có vecto chỉ phương \(\overrightarrow u \left( {1;2; - 2} \right).\) Đường phân giác của góc nhọn tạo bởi d và \(\Delta \) có phương trình là
Đáp án: B Phương pháp giải: Nhận thấy hai đường thẳng này cắt nhau tại A. Lấy 1 điểm B thuộc vào đường thẳng d ; 1 điểm C thuộc vào đường thẳng \(\Delta \) ; khi đó ta có AB = AC. Gọi I là trung điểm của BC thì đường thẳng đi qua A và I chính là đường phân giác cần tìm Lời giải chi tiết: Có \(d \cap \Delta = A\left( {1; - 3;5} \right)\) . Phương trình đường thẳng \(\Delta \) có dạng : \(\left\{ \begin{array}{l}x = 1 + t\\y = - 3 + 2t\\z = 5 - 2t\end{array} \right.. \Rightarrow C \in \left( \Delta \right):C\left( {2; - 1;3} \right)\) \(AC = \sqrt {1 + 4 + 4} = 3 \Rightarrow A{C^2} = 9\) Gọi \(B \in \left( d \right):B\left( {1 + 3t; - 3;5 + 4t} \right)\) sao cho \(AB = AC\) Ta có : \(A{B^2} = 9{t^2} + 16{t^2} = 25{t^2}\) Lại có : \(A{B^2} = A{C^2} \Leftrightarrow 25{t^2} = 9 \Leftrightarrow t = \pm \frac{3}{5}.\) +) TH1 : \(t = \frac{3}{5} \Rightarrow B\left( {\frac{{14}}{5}; - 3;\frac{{37}}{5}} \right);\overrightarrow {AB} = \left( {\frac{9}{5};0;\frac{{12}}{5}} \right);\overrightarrow {AC} = \left( {1;2; - 2} \right) \Rightarrow \overrightarrow {AB} .\overrightarrow {AC} = - 3 < 0\left( {ktm} \right)\) +) TH2 : \(t = - \frac{3}{5} \Rightarrow B\left( {\frac{{ - 4}}{5}; - 3;\frac{{13}}{5}} \right)\) Gọi I là trung điểm của BC khi đó ta có : \(I\left( {\frac{3}{5}; - 2;\frac{{14}}{5}} \right);\overrightarrow {AI} = \left( {\frac{{ - 2}}{5};1; - \frac{{11}}{5}} \right) \Rightarrow {\overrightarrow u _{AI}} = \left( {2; - 5;11} \right)\) Khi đó phương trình đường thẳng AI có dạng : \(\left\{ \begin{array}{l}x = 1 + 2t\\y = - 3 - 5t\\z = 5 + 11t\end{array} \right.;\,\,\,t = 1 \Rightarrow D\left( { - 1;2; - 6} \right)\) . Khi đó thì phương trình đường phân giác cần tìm có thể viết dưới dạng : \(\left\{ \begin{array}{l}x = - 1 + 2t\\y = 2 - 5t\\z = - 6 + 11t\end{array} \right.\). Chọn B. Câu hỏi 19 : Trong không gian, cho hai đường thẳng \(\Delta :\,\,\dfrac{x}{1} = \dfrac{y}{1} = \dfrac{{z - 1}}{1},\,\,\Delta ':\,\,\dfrac{{x - 1}}{1} = \dfrac{y}{2} = \dfrac{z}{1}\). Xét điểm \(M\) thay đổi. Gọi \(a,\,\,b\) lần lượt là khoảng cách từ \(M\) đến \(\Delta \) và \(\Delta '\). Biểu thức \({a^2} + 2{b^2}\) đạt giá trị nhỏ nhất khi và chỉ khi \(M \equiv M\left( {{x_0};{y_0};{z_0}} \right)\) . Khi đó \({x_0} + {y_0}\) bằng:
Đáp án: A Phương pháp giải: +) Gọi \(PQ\) là đoạn vuông góc chung của \(\Delta \) và \(\Delta '\). Xác định tọa độ các điểm \(P,Q\). +) Gọi \(H,\,\,K\) lần lượt là hình chiếu của \(M\) trên \(\Delta ,\,\,\Delta '\), đánh giá \(a + b \ge PQ\). +) Sử dụng BĐT \(\dfrac{{{a^2}}}{x} + \dfrac{{{b^2}}}{y} \ge \dfrac{{{{\left( {a + b} \right)}^2}}}{{x + y}}\). Dấu “=” xảy ra \( \Leftrightarrow \dfrac{a}{x} = \dfrac{b}{y}\). Lời giải chi tiết:
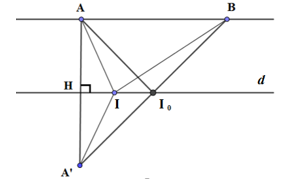
Gọi \(H,\,\,K\) lần lượt là hình chiếu của \(M\) trên \(\Delta ,\,\,\Delta '\) \( \Rightarrow MH = a,\,\,MK = b\). Gọi \(PQ\) là đoạn vuông góc chung của \(\Delta \) và \(\Delta '\). Lấy \(P\left( {t;t;t + 1} \right) \in \left( \Delta \right);\,\,Q\left( {t' + 1;2t';t'} \right) \in \left( {\Delta '} \right)\) ta có: \(\overrightarrow {PQ} = \left( {t' - t + 1;\,\,2t' - t;\,\,t' - t - 1} \right)\). Gọi 2 VTCP của \(\Delta \) và \(\Delta '\) lần lượt là \(\overrightarrow {{u_1}} = \left( {1;1;1} \right);\,\,\overrightarrow {{u_2}} = \left( {1;2;1} \right)\) \(\left\{ \begin{array}{l}\overrightarrow {PQ} .\overrightarrow {{u_1}} = 0\\\overrightarrow {PQ} .\overrightarrow {{u_2}} = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}t' - t + 1 + 2t' - t + t' - t - 1 = 0\\t' - t + 1 + 4t' - 2t + t' - t - 1 = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}4t' - 3t = 0\\6t' - 4t = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}t' = 0\\t = 0\end{array} \right.\) \( \Rightarrow P\left( {0;0;1} \right);\,\,Q\left( {1;0;0} \right)\). Ta có \(a + b \ge HK \ge PQ = \sqrt {{1^2} + {1^2}} = \sqrt 2 \) Áp dụng BĐT Bunhiacopxki ta có \({a^2} + 2{b^2} = \dfrac{{{a^2}}}{1} + \dfrac{{{b^2}}}{{\dfrac{1}{2}}} \ge \dfrac{{{{\left( {a + b} \right)}^2}}}{{1 + \dfrac{1}{2}}} \ge \dfrac{{{{\left( {\sqrt 2 } \right)}^2}}}{{\dfrac{3}{2}}} = \dfrac{4}{3}\). Dấu “=” xảy ra \( \Leftrightarrow \left\{ \begin{array}{l}\dfrac{a}{1} = \dfrac{b}{{\dfrac{1}{2}}}\\M \in PQ\end{array} \right. \Rightarrow \left\{ \begin{array}{l}a = 2b\\M \in PQ\end{array} \right. \Leftrightarrow \overrightarrow {MP} = - 2\overrightarrow {MQ} \). Gọi \(M\left( {a;b;c} \right) \Rightarrow \overrightarrow {MP} = \left( { - a; - b;1 - c} \right);\,\,\overrightarrow {MQ} = \left( {1 - a; - b; - c} \right)\) \( \Rightarrow \left\{ \begin{array}{l} - a = - 2 + 2a\\ - b = 2b\\1 - c = 2c\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = \dfrac{2}{3}\\b = 0\\c = \dfrac{1}{3}\end{array} \right. \Rightarrow M\left( {\dfrac{2}{3};0;\dfrac{1}{3}} \right) \Rightarrow {x_0} = \dfrac{2}{3};\,\,{y_0} = 0 \Rightarrow {x_0} + {y_0} = \dfrac{2}{3}\). Chọn A. Câu hỏi 20 : Trong không gian Oxyz, cho hai điểm \(A\left( {1; - 1;2} \right),B\left( {3; - 4; - 2} \right)\) và đường thẳng \(d:\left\{ \begin{array}{l}x = 2 + 4t\\y = - 6t\\z = - 1 - 8t\end{array} \right.\). Điểm \(I\left( {a;b;c} \right)\) thuộc d là điểm thỏa mãn \(IA + IB\) đạt giá trị nhỏ nhất. Khi đó \(T = a + b + c\) bằng:
Đáp án: D Phương pháp giải: Lời giải chi tiết: \(d:\left\{ \begin{array}{l}x = 2 + 4t\\y = \,\,\,\,\, - 6t\\z = - 1 - 8t\end{array} \right.\) có 1 VTCP \(\overrightarrow u \left( {4; - 6; - 8} \right)\) \(A\left( {1; - 1;2} \right),B\left( {3; - 4; - 2} \right) \Rightarrow \overrightarrow {AB} = \left( {2; - 3; - 4} \right)\) Ta có: \(\overrightarrow {AB} = \left( {2; - 3; - 4} \right)\) cùng phương với \(\overrightarrow u \left( {4; - 6; - 8} \right)\). Mà \(A\left( {1; - 1;2} \right) \notin d \Rightarrow AB//d \Rightarrow A,B,d\) đồng phẳng * Xét mặt phẳng chứa \(AB\) và \(d\): Gọi \(A'\) là điểm đối xứng của \(A\) qua \(\Delta \); \(\left( \alpha \right)\) là mặt phẳng qua \(A\), vuông góc với d Khi đó, giao điểm \(H\) của \(\Delta \) với \(\left( \alpha \right)\) là trung điểm của \(AA'\) \(\left( \alpha \right)\) có 1 VTPT \(\overrightarrow n \left( {2; - 3; - 4} \right)\), đi qua \(A\left( {1; - 1;2} \right)\), có phương trình: \(2\left( {x - 1} \right) - 3\left( {y + 1} \right) - 4\left( {z - 2} \right) = 0 \Leftrightarrow 2x - 3y - 4z + 3 = 0\) \(H \in d:\left\{ \begin{array}{l}x = 2 + 4t\\y = \,\,\,\,\,\, - 6t\\z = - 1 - 8t\end{array} \right.\,\, \Rightarrow \)Giả sử \(H\left( {2 + 4t; - 6t; - 1 - 8t} \right)\) \(H \in \left( \alpha \right)\,\, \Rightarrow 2\left( {2 + 4t} \right) - 3\left( { - 6t} \right) - 4\left( { - 1 - 8t} \right) + 3 = 0 \Leftrightarrow 58t + 11 = 0 \Leftrightarrow t = - \dfrac{{11}}{{58}}\,\,\)\( \Rightarrow H\left( {\dfrac{{36}}{{29}};\dfrac{{33}}{{29}};\dfrac{{15}}{{29}}} \right)\) Ta có: \(IA + IB = IA' + IB \ge A'B\,\, \Rightarrow {\left( {IA + IB} \right)_{\min }} = A'B\) khi và chỉ khi \(I\) trùng với \({I_0}\) là giao điểm của \(A'B\) và \(\Delta \) \(H{I_0}\) là đường trung bình của tam giác \(A'AB \Rightarrow \overrightarrow {H{I_0}} = \dfrac{1}{2}\overrightarrow {AB} \Leftrightarrow \left\{ \begin{array}{l}{x_{{I_0}}} - \dfrac{{36}}{{29}} = \dfrac{1}{2}.2\\{y_{{I_0}}} - \dfrac{{33}}{{29}} = \dfrac{1}{2}.\left( { - 3} \right)\\{z_{{I_0}}} - \dfrac{{15}}{{29}} = \dfrac{1}{2}.\left( { - 4} \right)\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{x_{{I_0}}} = \dfrac{{65}}{{29}}\\{y_{{I_0}}} = \dfrac{{ - 21}}{{58}}\\{z_{{I_0}}} = - \dfrac{{43}}{{29}}\end{array} \right.\) \( \Rightarrow {I_0}\left( {\dfrac{{65}}{{29}}; - \dfrac{{21}}{{58}}; - \dfrac{{43}}{{29}}} \right)\) Vậy, để \(IA + IB\) đạt giá trị nhỏ nhất thì \(I\left( {\dfrac{{65}}{{29}}; - \dfrac{{21}}{{58}}; - \dfrac{{43}}{{29}}} \right) \Rightarrow a + b + c = \dfrac{{65}}{{29}} - \dfrac{{21}}{{58}} - \dfrac{{43}}{{29}} = - \dfrac{{21}}{{58}}\). Chọn: D Câu hỏi 21 : Cho \(A\left( {1;4;2} \right),\,\,B\left( { - 1;2;4} \right),\,\,\left( \Delta \right):\,\,\dfrac{{x - 1}}{{ - 1}} = \dfrac{{y + 2}}{1} = \dfrac{z}{2}\). Tìm \(M \in \left( \Delta \right)\) để \({\left( {M{A^2} + M{B^2}} \right)_{\min }}\).
Đáp án: A Phương pháp giải: Lời giải chi tiết: * \(M \in \left( \Delta \right) \Rightarrow M\left( { - t + 1;t - 2;2t} \right)\). * \(T = M{A^2} + M{B^2} = \left[ {{t^2} + {{\left( {6 - t} \right)}^2} + {{\left( {2t - 2} \right)}^2} + {{\left( { - t + 2} \right)}^2} + {{\left( {t - 4} \right)}^2} + {{\left( {2t - 4} \right)}^2}} \right]\) \( = 12{t^2} - 48t + 76\) * \({T_{\min }} \Leftrightarrow t = - \dfrac{b}{{2a}} = \dfrac{{4.8}}{{2.12}} = 2\) \( \Rightarrow M\left( { - 1;0;4} \right)\). Chọn A. Câu hỏi 22 : Cho \(A\left( {1; - 1;2} \right),\,\,\left( Q \right):\,\,2x - y - z + 3 = 0,\,\,\left( \Delta \right):\,\,\dfrac{{x + 1}}{1} = \dfrac{{y - 1}}{{ - 2}} = \dfrac{z}{2}\). Lập phương trình \(\left( d \right)\) qua \(A\), \(d//\left( Q \right)\) và \(\left( d \right)\) tạo với \(\left( \Delta \right)\) góc nhỏ nhất.
Đáp án: A Phương pháp giải: Lời giải chi tiết: * Giả sử \(\overrightarrow {{a_d}} = \left( {a;b;c} \right)\,\,\left( {Dk:\,\,{a^2} + {b^2} + {c^2} \ne 0} \right)\). * \(\left\{ \begin{array}{l}\overrightarrow {{a_d}} = \left( {a;b;c} \right)\\\overrightarrow {{n_Q}} = \left( {2; - 1; - 1} \right)\end{array} \right.;\,\,\overrightarrow {{n_Q}} \bot \overrightarrow {{a_d}} \Rightarrow \overrightarrow {{n_Q}} .\overrightarrow {{a_d}} = 0\) \( \Leftrightarrow 2a - b - c = 0 \Leftrightarrow c = 2a - b \Rightarrow \overrightarrow {{a_d}} = \left( {a;b;2a - b} \right)\) * \(\overrightarrow {{a_\Delta }} = \left( {1; - 2;2} \right)\). Ta có: \(\cos \left( {\Delta ;d} \right) = \left| {\dfrac{{\overrightarrow {{a_d}} .\overrightarrow {{a_\Delta }} }}{{\left| {\overrightarrow {{a_d}} } \right|.\left| {\overrightarrow {{a_\Delta }} } \right|}}} \right| = \left| {\dfrac{{a - 2b + 2\left( {2a - b} \right)}}{{\sqrt {{a^2} + {b^2} + {{\left( {2a - b} \right)}^2}} \sqrt 9 }}} \right| = \cos \alpha \) * Đặt \(t = \dfrac{a}{b}\,\,\left( {t \in \mathbb{R}} \right)\). Ta có: \(\cos \alpha = \dfrac{1}{3}\dfrac{{\left| {5t - 4} \right|}}{{\sqrt {5{t^2} - 4t + 2} }} = \dfrac{1}{3}\sqrt {\dfrac{{{{\left( {5t - 4} \right)}^2}}}{{5{t^2} - 4t + 2}}} \). Đặt \(f\left( t \right) = \dfrac{{{{\left( {5t - 4} \right)}^2}}}{{5{t^2} - 4t + 2}} \Rightarrow f'\left( t \right) = \dfrac{{2\left( {5t - 4} \right)\left( {10t + 2} \right)}}{{{{\left( {5{t^2} - 4t + 2} \right)}^2}}}\) \(f'\left( t \right) = 0 \Leftrightarrow \left[ \begin{array}{l}t = \dfrac{4}{5}\\t = - \dfrac{1}{5}\end{array} \right.\) * \(f\left( {\dfrac{4}{5}} \right) = 0,\,\,f\left( { - \dfrac{1}{5}} \right) = \dfrac{{25}}{3}\). Hàm số \(\cos \alpha \) nghịch biến trên \(\left[ {{0^0};{{90}^0}} \right]\) \( \Rightarrow f{\left( t \right)_{\min }} \Leftrightarrow t = - \dfrac{1}{5}\). Chọn \(a = 1 \Rightarrow b = - 5 \Rightarrow c = 7\). Chọn A. Câu hỏi 23 : Trong không gian \(Oxyz\), cho mặt cầu \({x^2} + {y^2} + {z^2} = 9\) và điểm \(M\left( {{x_0};{y_0};{z_0}} \right) \in \left( d \right):\,\,\left\{ \begin{array}{l}x = 1 + t\\y = 1 + 2t\\z = 2 - 3t\end{array} \right.\) . Ba điểm \(A,\,\,B,\,\,C\) phân biệt cùng thuộc mặt cầu sao cho \(MA,\,\,MB,\,\,MC\) là tiếp tuyến của mặt cầu. Biết rằng mặt phẳng \(\left( {ABC} \right)\) đi qua \(D\left( {1;1;2} \right)\). Tổng \(T = x_0^2 + y_0^2 + z_0^2\) bằng:
Đáp án: B Phương pháp giải: Lời giải chi tiết:
Mặt cầu \({x^2} + {y^2} + {z^2} = 9\) có tâm \(O\left( {0;0;0} \right)\) và bán kính \(R = 3\). Gọi T là giao điểm của tia ID với mặt cầu. Ta có: \(O{T^2} = OI.OM \Leftrightarrow OI.OM = {3^2} = 9\) \(M\left( {{x_0};{y_0};{z_0}} \right) \Rightarrow \overrightarrow {{n_{\left( P \right)}}} = \overrightarrow {OM} = \left( {{x_0};{y_0};{z_0}} \right)\) Phương trình (P) là: \({x_0}\left( {x - 1} \right) + {y_0}\left( {y - 1} \right) + {z_0}\left( {z - 2} \right) = 0\) \(\begin{array}{l}OI = d\left( {O;\left( P \right)} \right) = \dfrac{{\left| {{x_0} + {y_0} + 2{z_0}} \right|}}{{\sqrt {x_0^2 + y_0^2 + z_0^2} }};\,\,OM = \sqrt {x_0^2 + y_0^2 + z_0^2} \\ \Rightarrow \dfrac{{\left| {{x_0} + {y_0} + 2{z_0}} \right|}}{{\sqrt {x_0^2 + y_0^2 + z_0^2} }}.\sqrt {x_0^2 + y_0^2 + z_0^2} = 9 \Rightarrow \left| {{x_0} + {y_0} + 2{z_0}} \right| = 9\end{array}\) Do nên giả sử \(M\left( {1 + t;1 + 2t;2 - 3t} \right)\) \( \Rightarrow \left| {1 + t + 1 + 2t + 4 - 6t} \right| = 9 \Leftrightarrow \left| {6 - 3t} \right| = 9 \Leftrightarrow \left[ \begin{array}{l}t = - 1\\t = 5\end{array} \right.\) \(t = - 1 \Rightarrow M\left( {0; - 1;5} \right) \Rightarrow \)\(T = x_0^2 + y_0^2 + z_0^2 = 26\) \(t = 5 \Rightarrow M\left( {6;11; - 13} \right) \Rightarrow \)\(T = x_0^2 + y_0^2 + z_0^2 = 326\) Chọn: B Câu hỏi 24 : Trong không gian \(Oxyz,\) cho ba đường thẳng \(d:\,\,\frac{x}{1} = \frac{y}{1} = \frac{{z + 1}}{{ - 2}};\,\,{\Delta _1}:\,\frac{{x - 3}}{2} = \frac{y}{1} = \frac{{z - 1}}{1};\,\) \({\Delta _2}:\,\frac{{x - 1}}{1} = \frac{{y - 2}}{2} = \frac{z}{1}.\) Đường thẳng \(\Delta \) vuông góc với \(d\) đồng thời cắt \({\Delta _1},\,{\Delta _2}\) tương ứng tại\(H,\,K\) sao cho độ dài \(HK\) nhỏ nhất. Biết rằng \(\Delta \) có một vecto chỉ phương \(\overrightarrow u = \left( {h;\,k;\,1} \right).\) Giá trị của \(h - k\) bằng:
Đáp án: A Phương pháp giải: +) Tham số hóa tọa độ điểm \(H \in {\Delta _1},\,\,K \in {\Delta _2}\). +) \(d \bot \Delta \Rightarrow \overrightarrow {{u_d}} .\overrightarrow {HK} = 0\). +) Tính độ dài \(HK\). Tìm điều kiện để \(HK\) nhỏ nhất. Lời giải chi tiết: Giả sử \(H\left( {3 + 2t;\,\,t;\,\,1 + t} \right) \in {\Delta _1},\,\,K\left( {1 + t';\,\,2 + 2t';\,\,t'} \right) \in {\Delta _2}\) ta có: \(\overrightarrow {HK} = \left( {t' - 2t - 2;\,\,2t' - t + 2;\,\,t' - t - 1} \right)\). Đường thẳng \(d\) có 1 VTCP là \(\overrightarrow {{u_d}} = \left( {1;1; - 2} \right)\). Vì \(d \bot \Delta \Rightarrow \overrightarrow {{u_d}} \bot \overrightarrow {HK} \Rightarrow \overrightarrow {{u_d}} .\overrightarrow {HK} = 0\) \(\begin{array}{l} \Leftrightarrow t' - 2t - 2 + 2t' - t + 2 - 2\left( {t' - t - 1} \right) = 0\\ \Leftrightarrow t' - t + 2 = 0 \Leftrightarrow t' = t - 2\end{array}\) Ta có \( \Rightarrow \overrightarrow {HK} = \left( { - t - 4;t - 2; - 3} \right) \Rightarrow H{K^2} = {\left( {t + 4} \right)^2} + {\left( {t - 2} \right)^2} + 9\) \( \Leftrightarrow H{K^2} = 2{t^2} + 4t + 29 = 2{\left( {t + 1} \right)^2} + 27 \ge 27\) \( \Leftrightarrow H{K_{\min }} = 3\sqrt 3 \Leftrightarrow t = - 1\). Khi đó \(\overrightarrow {HK} = \left( { - 3; - 3; - 3} \right)//\left( {1;1;1} \right)\). Suy ra đường thẳng \(\Delta \) nhận \(\overrightarrow u \left( {1;1;1} \right)\) là 1 VTCP \( \Rightarrow h = k = 1\). Vậy \(h - k = 1 - 1 = 0\). Chọn A. Câu hỏi 25 : Cho \(A\left( {2;0;1} \right),\,\,B\left( {2; - 1;0} \right),\,\,C\left( {1;0;1} \right),\,\,\left( \Delta \right):\,\,\dfrac{x}{1} = \dfrac{y}{2} = \dfrac{z}{3}\). Tìm \(M \in \left( \Delta \right)\) để \({\left| {\overrightarrow {MA} + \overrightarrow {MB} + \overrightarrow {MC} } \right|_{\min }}\).
Đáp án: B Phương pháp giải: Lời giải chi tiết: * \(M \in \left( \Delta \right) \Rightarrow M\left( {t;2t;3t} \right)\) * \(P = \left| {\overrightarrow {MA} + \overrightarrow {MB} + \overrightarrow {MC} } \right|\) \(\begin{array}{l} = \left| {\left( {2 - t; - 2t;1 - 3t} \right) + \left( {2 - t; - 1 - 2t; - 3t} \right) + \left( {1 - t; - 2t;1 - 3t} \right)} \right|\\ = \left| {\left( {5 - 3t; - 1 - 6t;2 - 9t} \right)} \right|\\ = \sqrt {{{\left( {5 - 3t} \right)}^2} + {{\left( { - 1 - 6t} \right)}^2} + {{\left( {2 - 9t} \right)}^2}} \\ = \sqrt {126{t^2} - 54t + 30} \end{array}\) * \({P_{\min }} \Leftrightarrow t = - \dfrac{b}{{2a}} = \dfrac{{5.4}}{{2.126}} = \dfrac{3}{{14}}\). \( \Rightarrow M\left( {\dfrac{3}{{14}};\dfrac{6}{{14}};\dfrac{9}{{14}}} \right)\). Chọn B. Câu hỏi 26 : Cho \(A\left( {5;4;3} \right),\,\,B\left( {6;7;2} \right),\,\,\left( \Delta \right):\,\,\dfrac{{x - 1}}{2} = \dfrac{{y - 2}}{3} = \dfrac{{z - 3}}{1}\). Tìm \(M \in \left( \Delta \right)\) để \({S_{\Delta ABM\,\,\min }}\).
Đáp án: C Phương pháp giải: Lời giải chi tiết: * Vì \(M \in \left( \Delta \right) \Rightarrow M\left( {2t + 1;3t + 2;t + 3} \right)\) * \(\left\{ \begin{array}{l}\overrightarrow {AM} = \left( {2t - 4;3t - 2;t} \right)\\\overrightarrow {AB} = \left( {1;3; - 1} \right)\end{array} \right. \Rightarrow \overrightarrow n = \left[ {\overrightarrow {AM} ;\overrightarrow {AB} } \right]\) \( \Rightarrow \overrightarrow n = \left( { - 6t + 2;3t - 4;3t - 10} \right)\) \(\begin{array}{l}*\,\,{S_{\Delta MAB}} = \dfrac{1}{2}\left| {\overrightarrow n } \right| = \dfrac{1}{2}\sqrt {{{\left( {6t - 2} \right)}^2} + {{\left( {3t - 4} \right)}^2} + {{\left( {3t - 10} \right)}^2}} \\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = \dfrac{1}{2}\sqrt {54{t^2} - 108t + 120} \end{array}\) * \({S_{\Delta MAB\,\,\min }} \Leftrightarrow t = - \dfrac{b}{{2a}} = \dfrac{{108}}{{2.54}} = 1\). \( \Rightarrow M\left( {3;5;4} \right)\). Chọn C. Câu hỏi 27 : Trong không gian tọa độ Oxyz, cho điểm A(1;2;4) và hai điểm M, B thỏa mãn \(MA.\overrightarrow {MA} + MB.\overrightarrow {MB} = \overrightarrow 0 .\) Giả sử điểm M thay đổi trên đường thẳng \(d:\dfrac{{x + 3}}{2} = \dfrac{{y - 1}}{2} = \dfrac{{z + 4}}{1}\). Khi đó điểm B thay đổi trên đường thẳng có phương trình là
Đáp án: D Phương pháp giải: Lời giải chi tiết: Theo bài ra ta có: \(MA.\overrightarrow {MA} + MB.\overrightarrow {MB} = \overrightarrow 0 \Leftrightarrow MA.\overrightarrow {MA} = - MB.\overrightarrow {MB} \Leftrightarrow \dfrac{{\overrightarrow {MA} }}{{\overrightarrow {MB} }} = - \dfrac{{MB}}{{MA}} < 0\). \( \Rightarrow M\) thuộc đoạn thẳng \(AB\). Dễ thấy khi \(M\) chạy trên \(d\) và \(M,\,\,B\) thỏa mãn \(MA.\overrightarrow {MA} + MB.\overrightarrow {MB} = \overrightarrow 0 \) thì \(B\) chạy trên đường thẳng \({d_1}//d\). Gọi \({M_1},\,\,{B_1}\) lần lượt là hình chiếu của \(A\) trên \(d,\,\,{d_1} \Rightarrow {M_1}A.\overrightarrow {{M_1}A} + {M_1}{B_1}.\overrightarrow {{M_1}{B_1}} = \overrightarrow 0 \). \({M_1} \in d \Rightarrow {M_1}\left( { - 3 + 2t;1 + 2t; - 4 + t} \right) \Rightarrow \overrightarrow {{M_1}A} = \left( {4 - 2t;1 - 2t;8 - t} \right)\). \(\overrightarrow {{M_1}A} .\overrightarrow {{u_d}} = 0 \Leftrightarrow 2\left( {4 - 2t} \right) + 2\left( {1 - 2t} \right) + 8 - t = 0 \Leftrightarrow t = 2\) \( \Rightarrow \left\{ \begin{array}{l}\overrightarrow {{M_1}A} = \left( {0; - 3;6} \right) \Rightarrow {M_1}A = 3\sqrt 5 \\{M_1}\left( {1;5; - 2} \right)\end{array} \right.\). Gọi \(\Delta \) là đường thẳng qua \(A\) và vuông góc với \({d_1} \Rightarrow \Delta \) đi qua \(A,\,\,{M_1}\). \( \Rightarrow Pt\Delta :\,\,\left\{ \begin{array}{l}x = 1\\y = 2 - t\\z = 4 + 2t\end{array} \right.;\,\,{B_1} \in \Delta \Rightarrow {B_1}\left( {1;2 - b;4 + 2b} \right)\). \( \Rightarrow \overrightarrow {{M_1}{B_1}} = \left( {0; - 3 - b;6 + 2b} \right) \Rightarrow {M_1}{B_1} = \sqrt {{{\left( { - 3 - b} \right)}^2} + {{\left( {6 + 2b} \right)}^2}} = \sqrt 5 \left| {b + 3} \right|\). \(\begin{array}{l}{M_1}A.\overrightarrow {{M_1}A} + {M_1}{B_1}.\overrightarrow {{M_1}{B_1}} = \overrightarrow 0 \Leftrightarrow 3\sqrt 5 \left( {0; - 3;6} \right) + \sqrt 5 \left| {b + 3} \right|\left( {0; - 3 - b;6 + 2b} \right) = \overrightarrow 0 \\ \Leftrightarrow \left\{ \begin{array}{l} - 9 + \left| {b + 3} \right|\left( { - 3 - b} \right) = 0\\18 + \left| {b + 3} \right|\left( {6 + 2b} \right) = 0\end{array} \right. \Leftrightarrow \left| {b + 3} \right|\left( {b + 3} \right) = - 9 \Rightarrow \left\{ \begin{array}{l}b + 3 < 0\\{\left( {b + 3} \right)^2} = 9\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}b < - 3\\\left[ \begin{array}{l}b + 3 = 3\\b + 3 = - 3\end{array} \right.\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}b < 3\\\left[ \begin{array}{l}b = 0\\b = - 6\end{array} \right.\,\,\left( {tm} \right)\end{array} \right. \Rightarrow \left[ \begin{array}{l}{B_1}\left( {1;2;4} \right)\,\,\left( {ktm\,\,do\,\, \equiv A} \right)\\{B_1}\left( {1;8; - 8} \right)\end{array} \right.\end{array}\) Dựa vào các đáp án ta thấy \({B_1} \in {d_1}:\dfrac{{x + 7}}{2} = \dfrac{y}{2} = \dfrac{{z + 12}}{1}\). Vậy khi điểm M thay đổi trên đường thẳng \(d:\dfrac{{x + 3}}{2} = \dfrac{{y - 1}}{2} = \dfrac{{z + 4}}{1}\) thì điểm B thay đổi trên đường thẳng có phương trình là \({d_1}:\dfrac{{x + 7}}{2} = \dfrac{y}{2} = \dfrac{{z + 12}}{1}\). Chọn D. Câu hỏi 28 : Trong không gian \(Oxyz\), cho hình thang cân \(ABCD\) có hai đáy \(AB,\,\,CD\) thỏa mãn \(CD = 2AB\) và diện tích bằng \(27\), đỉnh \(A\left( { - 1; - 1;0} \right)\), phương trình đường thẳng chứa cạnh \(CD\) là \(\dfrac{{x - 2}}{2} = \dfrac{{y + 1}}{2} = \dfrac{{z - 3}}{1}\). Tìm tọa độ điểm \(D\) biết hoành độ điểm \(B\) lớn hơn hoành độ điểm \(A\).
Đáp án: D Phương pháp giải: Lời giải chi tiết: Gọi \(\overrightarrow u \left( {2;2;1} \right)\) là 1 VTCP của đường thẳng \(CD\). Vì \(AB\parallel CD\) nên \(\overrightarrow u \left( {2;2;1} \right)\) cũng là 1 VTCP của đường thẳng \(AB\). Suy ra phương trình đường thẳng chứa cạnh \(AB\) là: \(\dfrac{{x + 1}}{2} = \dfrac{{y + 1}}{2} = \dfrac{z}{1}\). Vì \(B \in AB \Rightarrow B\left( { - 1 + 2t; - 1 + 2t;t} \right)\) \(\left( { - 1 + 2t > - 1 \Leftrightarrow t > 0} \right)\). Lấy \(M\left( {2; - 1;3} \right) \in CD\), ta có: \(\overrightarrow {AM} = \left( {3;0;3} \right) \Rightarrow \left[ {\overrightarrow {AM} ;\overrightarrow u } \right] = \left( {6; - 3; - 6} \right)\). \(\begin{array}{l} \Rightarrow d\left( {A;CD} \right) = \dfrac{{\left| {\left[ {\overrightarrow {AM} ;\overrightarrow u } \right]} \right|}}{{\left| {\overrightarrow u } \right|}} = \dfrac{{\sqrt {{6^2} + {{\left( { - 3} \right)}^2} + {{\left( { - 6} \right)}^2}} }}{{\sqrt {{2^2} + {2^2} + {1^2}} }} = 3\\{S_{ABCD}} = \dfrac{{\left( {AB + CD} \right).d\left( {A;CD} \right)}}{2} \Rightarrow 27 = \dfrac{{\left( {AB + 2AB} \right).3}}{2}\\ \Leftrightarrow 3AB = 18 \Leftrightarrow AB = 6 \Leftrightarrow A{B^2} = 36\\ \Leftrightarrow {\left( { - 1 + 2t + 1} \right)^2} + {\left( { - 1 + 2t + 1} \right)^2} + {\left( {t - 0} \right)^2} = 36\\ \Leftrightarrow 4{t^2} + 4{t^2} + {t^2} = 36 \Leftrightarrow {t^2} = 4 \Leftrightarrow \left[ \begin{array}{l}t = 2\,\,\,\left( {tm} \right)\\t = - 2\,\,\left( {ktm} \right)\end{array} \right.\end{array}\) Vậy \(B\left( {3;3;2} \right)\). Chọn D. Câu hỏi 29 : Cho đường thẳng \({d_1}:\,\,\left\{ \begin{array}{l}x = 4 - 2t\\y = t\\z = 3\end{array} \right.\,\,\left( {t \in \mathbb{R}} \right)\) và \({d_2}:\,\,\left\{ \begin{array}{l}x = 1\\y = t'\\z = - t'\end{array} \right.\,\,\left( {t' \in \mathbb{R}} \right)\). Phương trình mặt cầu có bán kính nhỏ nhất tiếp xúc với cả hai đường thẳng \(\left( {{d_1}} \right),\,\,\left( {{d_2}} \right)\) là:
Đáp án: D Phương pháp giải: - Mặt cầu có bán kính nhỏ nhất tiếp xúc với cả hai đường thẳng \(\left( {{d_1}} \right),\,\,\left( {{d_2}} \right)\) nhận đoạn vuông góc chung của hai đường thẳng \(\left( {{d_1}} \right),\,\,\left( {{d_2}} \right)\) là đường kính. - Tìm đoạn vuông góc chung AB của \(\left( {{d_1}} \right),\,\,\left( {{d_2}} \right)\). - Tham số hóa tọa độ điểm A, B. Giải hệ phương trình \(\left\{ \begin{array}{l}\overrightarrow {AB} .\overrightarrow {{u_1}} = 0\\\overrightarrow {AB} .\overrightarrow {{u_2}} = 0\end{array} \right.\) với \(\overrightarrow {{u_1}} ,\,\,\overrightarrow {{u_2}} \) lần lượt là VTCP của \(\left( {{d_1}} \right),\,\,\left( {{d_2}} \right)\). - Viết phương trình mặt cầu. Lời giải chi tiết: Gọi \(\overrightarrow {{u_1}} = \left( { - 2;1;0} \right)\) và \(\overrightarrow {{u_2}} = \left( {0;1; - 1} \right)\) lần lượt là 1 VTCP của \(\left( {{d_1}} \right),\,\,\left( {{d_2}} \right)\). Gọi AB là đoạn vuông góc chung của \(\left( {{d_1}} \right),\,\,\left( {{d_2}} \right)\), với \(A\left( {4 - 2t;t;3} \right) \in {d_1}\), \(B\left( {1;t'; - t'} \right) \in {d_2}\). Ta có: \(\overrightarrow {AB} = \left( { - 3 + 2t;\,\,t' - t;\,\, - t' - 3} \right)\). Vì AB là đoạn vuông góc chung của \(\left( {{d_1}} \right),\,\,\left( {{d_2}} \right)\) nên \(\left\{ \begin{array}{l}AB \bot {d_1}\\AB \bot {d_2}\end{array} \right.\). \( \Rightarrow \left\{ \begin{array}{l}\overrightarrow {AB} .\overrightarrow {{u_1}} = 0\\\overrightarrow {AB} .\overrightarrow {{u_2}} = 0\end{array} \right. \Rightarrow \left\{ \begin{array}{l}\left( {2t - 3} \right).\left( { - 2} \right) + t' - t = 0\\t' - t + t' + 3 = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}t = 1\\t' = - 1\end{array} \right.\) \( \Rightarrow A\left( {2;1;3} \right),\,\,B\left( {1; - 1;1} \right)\). Mặt cầu có bán kính nhỏ nhất tiếp xúc với cả hai đường thẳng \(\left( {{d_1}} \right),\,\,\left( {{d_2}} \right)\) nhận AB là đường kính. \( \Rightarrow \) Tâm mặt cầu là trung điểm của AB, có tọa độ \(I\left( {\dfrac{3}{2};0;2} \right)\), bán kính \(R = IA = \sqrt {\dfrac{1}{4} + 1 + 1} = \dfrac{3}{2}\). Vậy phương trình mặt cầu cần tìm là: \({\left( {x - \dfrac{3}{2}} \right)^2} + {y^2} + {\left( {z - 2} \right)^2} = \dfrac{9}{4}\). Chọn D. Câu hỏi 30 : Trong không gian Oxyz, cho hai điểm \(A\left( {1;2; - 3} \right)\), \(M\left( { - 2; - 2;1} \right)\) và đường thẳng d có phương trình \(\dfrac{{x + 1}}{2} = \dfrac{{y - 5}}{2} = \dfrac{z}{{ - 1}}\). Phương trình đường thẳng \(d'\) đi qua M và vuông góc với d sao cho khoảng cách từ điểm A đến d’ nhỏ nhất là
Đáp án: D Phương pháp giải: - Tìm \(\left( P \right)\) là mặt phẳng chứa d’ và vuông góc với d. - Tìm hình chiếu của A trên mặt phẳng \(\left( P \right)\). - Tìm phương trình đường thẳng d’. Lời giải chi tiết: +)Gọi \(\left( P \right)\) là mặt phẳng chứa d’ và vuông góc với \(d:\dfrac{{x + 1}}{2} = \dfrac{{y - 5}}{2} = \dfrac{z}{{ - 1}}\) Mặt phẳng \(\left( P \right)\) có vecto pháp tuyến là \(\overrightarrow n = \left( {2;2; - 1} \right)\) và đi qua \(M\left( { - 2; - 2;1} \right)\) có phương trình là \(2x + 2y - z + 9 = 0\) +)Đường thẳng m đi qua điểm A và vuông góc vói mặt phẳng \(\left( P \right)\) Nên đường thẳng m có vecto chỉ phương là \(\left( {2;2; - 1} \right)\) và đi qua \(A\left( {1;2; - 3} \right)\) có dạng \(\dfrac{{x - 1}}{2} = \dfrac{{y - 2}}{2} = \dfrac{{z + 3}}{{ - 1}}\) Gọi B là giao điểm của đường thẳng m và mặt phẳng \(\left( P \right)\) \(\begin{array}{l}B\left( {2t + 1;2t + 2; - t - 3} \right) \in \left( P \right):2x + 2y - z + 9 = 0 \Rightarrow t = - 2\\ \Rightarrow B\left( { - 3; - 2; - 1} \right)\end{array}\) Để khoảng cách từ điểm A đến đường thẳng d’ là nhỏ nhất thì d’ đi qua \(B\left( { - 3; - 2; - 1} \right)\) và \(M\left( { - 2; - 2;1} \right)\) Khi đó \(\overrightarrow {BM} = \left( {1;0;2} \right)\) Phương trình đường thẳng d’ là \(\left\{ \begin{array}{l}x = - 2 + t\\y = - 2\\z = 1 + 2t\end{array} \right.\) Chọn D. Quảng cáo
|