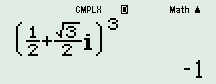30 bài tập phương trình bậc hai với hệ số thực mức độ vận dụng, vận dụng caoLàm bàiQuảng cáo
Câu hỏi 1 : Tập nghiệm của phương trình \({z^4} - {z^3} + \dfrac{{{z^2}}}{2} + z + 1 = 0\) trên tập số phức là:
Đáp án: A Lời giải chi tiết: \({z^4} - {z^3} + \dfrac{{{z^2}}}{2} + z + 1 = 0\) (1) +) Với \(z = 0\) thì \(1 = 0\) ( vô lí) \( \Rightarrow z = 0\) không là nghiệm của phương trình (1) +) Với \(z \ne 0\), chia cả 2 vế của phương trình (1) cho \({z^2}\) , ta được: \(\left( {{z^2} + \dfrac{1}{{{z^2}}}} \right) - \left( {z - \dfrac{1}{z}} \right) + \dfrac{1}{2} = 0{\text{ }}(2)\) Đặt \(t = z - \dfrac{1}{z}\) khi đó: \({t^2} = {z^2} + \dfrac{1}{{{z^2}}} - 2 \Leftrightarrow {z^2} + \dfrac{1}{{{z^2}}} = {t^2} + 2\) Phương trình (2) có dạng: \({t^2} - t + \dfrac{5}{2} = 0\)(3) Ta có: \(\Delta = 1 - 4.\dfrac{5}{2} = - 9 = 9{i^2} \Rightarrow t = \dfrac{{1 + 3i}}{2};t = \dfrac{{1 - 3i}}{2}\) +) Nếu \(t = \dfrac{{1 + 3i}}{2} \Leftrightarrow z - \dfrac{1}{z} = \dfrac{{1 + 3i}}{2} \Leftrightarrow 2{z^2} - (1 + 3i)z - 2 = 0\) Có \(\Delta = {(1 + 3i)^2} + 16 = 8 + 6i = {(3 + i)^2} \Rightarrow {z_1} = 1 + i;{z_2} = - \dfrac{1}{2} + \dfrac{i}{2}\) +) Nếu \(t = \dfrac{{1 - 3i}}{2} \Leftrightarrow z - \dfrac{1}{z} = \dfrac{{1 - 3i}}{2} \Leftrightarrow 2{z^2} - (1 - 3i)z - 2 = 0\) Có \(\Delta = {(1 - 3i)^2} + 16 = 8 - 6i = {(3 - i)^2} \Rightarrow {z_3} = 1 - i;{z_4} = - \dfrac{1}{2} - \dfrac{i}{2}\) Vậy tập nghiệm của phương trình là: \(\left\{ {1 + i;1 - i; - \dfrac{1}{2} + \dfrac{i}{2}; - \dfrac{1}{2} - \dfrac{i}{2}} \right\}\) Chọn A Câu hỏi 2 : Cho phương trình \({z^2} + bz + c = 0\) ẩn z và b, c là tham số thuộc tập số thực. Biết phương trình nhận\(z = 1 + i\) là một nghiệm. Tính \(T = b + c.\)
Đáp án: A Phương pháp giải: - Thay số phức \(z = 1 + i\) vào phương trình và biến đổi. - Một số phức bằng 0 khi và chỉ khi nó có phần thực và phần ảo cùng bằng 0. Lời giải chi tiết: Vì \(z = 1 + i\) là một nghiệm của phương trình \({z^2} + bz + c = 0\) nên ta có: \(\begin{array}{l}\,\,\,\,\,\,{\left( {1 + i} \right)^2} + b\left( {1 + i} \right) + c = 0\\ \Leftrightarrow 2i + b + bi + c = 0\\ \Leftrightarrow b + c + \left( {b + 2} \right)i = 0\\ \Leftrightarrow \left\{ \begin{array}{l}b + c = 0\\b + 2 = 0\end{array} \right.\end{array}\) Vậy \(T = b + c = 0\). Chọn A. Câu hỏi 3 : Phương trình \({z^2} + az + b = 0\left( {a,b \in \mathbb{R}} \right)\) có một nghiệm phức \(z = 1 - 3i\). Khi đó \(2{a^3} + 2{b^3} + 3\) bằng
Đáp án: B Phương pháp giải: - Phương trình bậc hai có 1 nghiệm \(z = a + bi\) thì nghiệm thứ 2 có dạng \(z = a - bi\). - Áp dụng định lý Vi-et: \({x_1} + {x_2} = \dfrac{{ - b}}{a}\), \({x_1}{x_2} = \dfrac{c}{a}\). Lời giải chi tiết: Phương trình \({z^2} + az + b = 0\) có 1 nghiệm phức \({z_1} = 1 - 3i \Rightarrow {z_2} = 1 + 3i\) Áp dụng định lý Vi-et ta có \(\left\{ \begin{array}{l}{z_1} + {z_2} = - a\\{z_1}.{z_2} = b\end{array} \right. \Rightarrow \left\{ \begin{array}{l}a = - 2\\b = 10\end{array} \right.\) Khi đó \(T = 2{a^3} + 2{b^3} + 3 = 1987\) Chọn B. Câu hỏi 4 : Trên tập số phức, phương trình \({z^2} - 6z + {2019^{2020}} + 9 = 0\) có một nghiệm là
Đáp án: B Phương pháp giải: Áp dụng định lý Vi-et: \(\left\{ \begin{array}{l}{z_1} + {z_2} = - \dfrac{b}{a}\\{z_1}{z_2} = \dfrac{c}{a}\end{array} \right.\). Lời giải chi tiết: Ta có \({z^2} - 6z + {2019^{2020}} + 9 = 0\)\( \Rightarrow \left\{ \begin{array}{l}{z_1} + {z_2} = 6\\{z_1}.{z_2} = {2019^{2020}} + 9\end{array} \right.\) Đặt \({z_1} = a + bi \Rightarrow {z_2} = a - bi\) Nên \({z_1} + {z_2} = 2a = 6 \Rightarrow a = 3\) Mà \({z_1}.{z_2} = {a^2} + {b^2} \Rightarrow {b^2} = {2019^{2020}} \Rightarrow b = \pm {2019^{1010}}\) Vậy \(z = 3 \pm {2019^{1010}}i.\) Chọn B. Câu hỏi 5 : Cho phương trình \({x^2} - 4x + \dfrac{c}{d} = 0\) (với phân số \(\dfrac{c}{d}\) tối giản) có hai nghiệm phức. Gọi A; B là hai điểm biểu diễn của hai nghiệm đó trên mặt phẳng Oxy. Biết tam giác OAB đều (O là gốc tọa độ). Tính \(P = c + 2d.\)
Đáp án: B Phương pháp giải: - Áp dụng định lý viet. - Sử dụng tính chất tam giác đều có ba cạnh bằng nhau. Lời giải chi tiết: Phương trình \({x^2} - 4x + \dfrac{c}{d} = 0\) có hai nghiệm phức \({z_1};{z_2}\) thỏa mãn \(\left\{ \begin{array}{l}{z_1} + {z_2} = 4\\{z_1}.{z_2} = \dfrac{c}{d}\end{array} \right.\) Ta có \({z_1} = a + bi \Rightarrow {z_2} = a - bi\) Nên \({z_1} + {z_2} = 2a = 4 \Rightarrow a = 2\) Đặt \(A\left( {2;b} \right);B\left( {2; - b} \right)\) Vì tam giác OAB đều nên \(OA = AB \Rightarrow 4 + {b^2} = 4{b^2} \Rightarrow {b^2} = \dfrac{4}{3}\) Mà \(\dfrac{c}{d} = {z_1}.{z_2} = {a^2} + {b^2} = 4 + \dfrac{4}{3} = \dfrac{{16}}{3}\) Nên \(\left\{ \begin{array}{l}c = 16\\d = 3\end{array} \right. \Rightarrow P = c + 2d = 22\) Chọn B. Câu hỏi 6 : Gọi z là một nghiệm của phương trình \({z^2} - z + 1 = 0\). Giá trị của biểu thức \(M = {z^{2019}} + {z^{2018}} + \dfrac{1}{{{z^{2019}}}} + \dfrac{1}{{{z^{2018}}}} + 5\) bằng
Đáp án: B Phương pháp giải: - Giải phương trình bậc hai tìm một nghiệm \(z\). - Tính \({z^3}\), từ đó phân tích \({z^{2019}},\,\,{z^{2018}}\) theo \({z^3}\) và tính giá trị biểu thức \(M\). Lời giải chi tiết: Ta có \({z^2} - z + 1 = 0 \Leftrightarrow \left[ \begin{array}{l}z = \dfrac{1}{2} + \dfrac{{\sqrt 3 }}{2}i\\z = \dfrac{1}{2} - \dfrac{{\sqrt 3 }}{2}i\end{array} \right.\). Chọn 1 nghiệm của phương trình trên là \(z = \dfrac{1}{2} + \dfrac{{\sqrt 3 }}{2}i\), ta có \({z^3} = - 1\).
Ta có: \(\begin{array}{l}{z^{2019}} = {\left( {{z^3}} \right)^{673}} = {\left( { - 1} \right)^{673}} = - 1\\{z^{2018}} = {\left( {{z^3}} \right)^{672}}.{z^2} = {\left( { - 1} \right)^{672}}.{\left( {\dfrac{1}{2} + \dfrac{{\sqrt 3 }}{2}i} \right)^2} = - \dfrac{1}{2} + \dfrac{{\sqrt 3 }}{2}i\end{array}\) Vậy \(\begin{array}{l}M = - 1 - \dfrac{1}{2} + \dfrac{{\sqrt 3 }}{2}i + \dfrac{1}{{ - 1}} + \dfrac{1}{{ - \dfrac{1}{2} + \dfrac{{\sqrt 3 }}{2}i}} + 5\\M = - 1 - \dfrac{1}{2} + \dfrac{{\sqrt 3 }}{2}i + \dfrac{1}{{ - 1}} - \dfrac{1}{2} - \dfrac{{\sqrt 3 }}{2}i + 5\\M = 2.\end{array}\) Chọn B. Câu hỏi 7 : Có bao nhiêu giá trị dương của số thực \(a\) sao cho phương trình \({z^2} + \sqrt 3 z + {a^2} - 2a = 0\) có nghiệm phức \({z_0}\) thỏa \(\left| {{z_0}} \right| = \sqrt 3 \).
Đáp án: B Phương pháp giải: Giải phương trình bậc hai với hệ số thực trên tập số phức. Lời giải chi tiết: TH1: Phương trình \({z^2} + \sqrt 3 z + {a^2} - 2a = 0\,\,\,\,\left( * \right)\) có nghiệm thực thỏa mãn \(\left| {{z_0}} \right| = \sqrt 3 \Leftrightarrow \left[ \begin{array}{l}{z_0} = \sqrt 3 \\{z_0} = - \sqrt 3 \end{array} \right.\). Nếu phương trình có nghiệm \({z_0} = \sqrt 3 \Leftrightarrow 3 + 3 + {a^2} - 2a = 0\) (vô nghiệm). Nếu phương trình có nghiệm \({z_0} = - \sqrt 3 \Leftrightarrow 3 - 3 + {a^2} - 2a = 0 \Leftrightarrow \left[ \begin{array}{l}a = 0\,\,\left( {ktm} \right)\\a = 2\,\,\left( {tm} \right)\end{array} \right.\). TH2: Phương trình \({z^2} + \sqrt 3 z + {a^2} - 2a = 0\,\,\,\,\left( * \right)\) có nghiệm phức, tức là có hai nghiệm phức liên hợp. Ta có: \(\Delta = 3 - 4\left( {{a^2} - 2a} \right) = - 4{a^2} + 8a + 3 < 0 \Leftrightarrow \left[ \begin{array}{l}a > \dfrac{{2 + \sqrt 7 }}{2}\\a < \dfrac{{2 - \sqrt 7 }}{2}\end{array} \right.\). Khi đó phương trình có 2 nghiệm phức \({z_{1,2}} = \dfrac{{ - \sqrt 3 \pm i\sqrt {4{a^2} - 8a - 3} }}{2}\). Theo bài ra ta có: \(\left| {{z_0}} \right| = \sqrt 3 \Rightarrow \dfrac{{3 + 4{a^2} - 8a - 3}}{4} = 3 \Leftrightarrow 4{a^2} - 8a - 12 = 0 \Leftrightarrow \left[ \begin{array}{l}a = - 1\,\,\left( {ktm} \right)\\a = 3\,\,\,\,\,\,\left( {tm} \right)\end{array} \right.\). Vậy, có 2 giá trị của a thỏa mãn yêu cầu bài toán. Chọn: B Câu hỏi 8 : Kí hiệu \({z_1}\,,\,{z_2}\)là 2 nghiệm phức của phương trình \({z^2} - 6z + 14 = 0\). Giá trị của \(z_1^2 + z_2^2\) bằng:
Đáp án: B Phương pháp giải: Sử dụng hệ thức Vi-et với phương trình bậc hai \(a{x^2} + bx + c = 0\) có hai nghiệm \({x_1},{x_2}\) là \(\left\{ \begin{array}{l}{x_1} + {x_2} = - \dfrac{b}{a}\\{x_1}{x_2} = \dfrac{c}{a}\end{array} \right.\) Lời giải chi tiết: Theo hệ thức Vi-ét ta có \(\left\{ \begin{array}{l}{z_1} + {z_2} = 6\\{z_1}{z_2} = 14\end{array} \right.\) Ta có \(z_1^2 + z_2^2 = {\left( {{z_1} + {z_2}} \right)^2} - 2{z_1}{z_2} = {6^2} - 2.14 = 8\) Chọn B. Câu hỏi 9 : Giả sử \({z_1},\,\,{z_2}\) là hai nghiệm phức của phương trình \({z^2} - 2z + 3 = 0\) và \(z = 2{z_1} + 2{z_2} + {z_1}{z_2}i.\) Khi đó \(\left| {\overline z } \right|\) bằng:
Đáp án: D Phương pháp giải: Áp dụng định lý Vi-et: \(\left\{ \begin{array}{l}{z_1} + {z_2} = - \dfrac{b}{a}\\{z_1}{z_2} = \dfrac{c}{a}\end{array} \right..\) Cho số phức \(z = a + bi\,\,\,\left( {a,\,\,b \in \mathbb{R}} \right) \Rightarrow \overline z = a - bi.\) Modun của số phức \(z = x + yi:\;\;\left| z \right| = \sqrt {{x^2} + {y^2}} .\) Lời giải chi tiết: Ta có: \({z_1},\,\,{z_2}\) là hai nghiệm phức của phương trình \({z^2} - 2z + 3 = 0\) \( \Rightarrow \) Áp dụng định lý Vi-et ta có: \(\left\{ \begin{array}{l}{z_1} + {z_2} = 2\\{z_1}{z_2} = 3\end{array} \right..\) \(\begin{array}{l} \Rightarrow z = 2{z_1} + 2{z_2} + {z_1}{z_2}i = 2\left( {{z_1} + {z_2}} \right) + {z_1}{z_2}i\\\,\,\,\,\,\,\,\,\,\,\, = 2.2 + 3i = 4 + 3i.\\ \Rightarrow \overline z = 4 - 3i\\ \Rightarrow \left| {\overline z } \right| = \sqrt {{4^2} + {{\left( { - 3} \right)}^2}} = 5.\end{array}\) Chọn D. Câu hỏi 10 : Gọi \({{z}_{1}},\,\,{{z}_{2}}\) là hai nghiệm của phương trình \(3{{z}^{2}}-z+4=0\). Khi đó \(P=\frac{{{z}_{1}}}{{{z}_{2}}}+\frac{{{z}_{2}}}{{{z}_{1}}}\)bằng
Đáp án: A Phương pháp giải: - Áp dụng định lí Vi – et, xác định tổng và tích hai nghiệm của phương trình bậc hai một ẩn \(a{{z}^{2}}+bz+c=0,\,\,a\ne 0\) Lời giải chi tiết: Xét phương trình \(3{{z}^{2}}-z+4=0\). Áp dụng định lý Vi-ét: \(\left\{ \begin{align} {{z}_{1}}+{{z}_{2}}=\frac{1}{3} \\ {{z}_{1}}{{z}_{2}}=\frac{4}{3} \\ \end{align} \right.\) \(P=\frac{{{z}_{1}}}{{{z}_{2}}}+\frac{{{z}_{2}}}{{{z}_{1}}}=\frac{{{z}_{1}}^{2}+{{z}_{2}}^{2}}{{{z}_{1}}{{z}_{2}}}=\frac{{{({{z}_{1}}+{{z}_{2}})}^{2}}-2{{z}_{1}}{{z}_{2}}}{{{z}_{1}}{{z}_{2}}}=\frac{{{\left( \frac{1}{3} \right)}^{2}}-2.\frac{4}{3}}{\frac{4}{3}}=\frac{\frac{1}{9}-\frac{8}{3}}{\frac{4}{3}}=-\frac{23}{12}\) Chọn: A Câu hỏi 11 : Tìm tham số thực \(m\) để phương trình: \({{z}^{2}}+(2-m)z+2=0\) có một nghiệm là \(z=1-i\)
Đáp án: B Phương pháp giải: Số phức \(z={{z}_{0}}\) là một nghiệm của phương trình \(f\left( z \right)=0 \) nếu \(f\left( {{z_0}} \right) = 0\) Lời giải chi tiết: Ta có \(z=1-i\) là nghiệm của phương trình nên: \({{\left( 1-i \right)}^{2}}+(2-m)(1-i)+2=0\) \(\begin{array}{l} \Leftrightarrow 1 - 2i + {i^2} + 2 - 2i - m + mi + 2 = 0\\ \Leftrightarrow ( - 1 + i)m = - 4 + 4i\\ \Leftrightarrow m = \frac{{ - 4 + 4i}}{{ - 1 + i}} = 4\end{array}\) Chọn B Câu hỏi 12 : Cho \(z=2+3i\) là một số phức. Hãy tìm một phương trình bậc \(2\) với hệ số thực nhận \(z\) và \(\overline{z}\) làm nghiệm
Đáp án: A Phương pháp giải: Phương trình bậc hai nhận \(z={{z}_{1}},z={{z}_{2}}\) làm nghiệm là: \(\left( z-{{z}_{1}} \right)\left( z-{{z}_{2}} \right)=0\) Lời giải chi tiết: Ta có: \(z=2+3i;\overline{z}=2-3i\) Nếu \(z\) và \(\overline{z}\) là \(2\) nghiệm của một phương trình thì: \(\left[ z-(2+3i) \right]\left[ z-(2-3i) \right]=0\) \(\begin{array}{l} \Leftrightarrow {z^2} - (2 - 3i)z - (2 + 3i)z + (2 + 3i)(2 - 3i) = 0\\ \Leftrightarrow {z^2} - 4z + 13 = 0\end{array}\) Chọn A Câu hỏi 13 : Gọi \({{z}_{1}},{{z}_{2}}\) là các nghiệm của phương trình: \(z+\frac{1}{z}=-1\). Giá trị của \(P={{z}_{1}}^{3}+{{z}_{2}}^{3}\) là:
Đáp án: C Phương pháp giải: - Biến đổi phương trình đưa về phương trình bậc hai. - Áp dụng định lý Vi-et cho phương trình bậc hai: \(\left\{ \begin{array}{l}{z_1} + {z_2} = - \frac{b}{a}\\{z_1}.{z_2} = \frac{c}{a}\end{array} \right.\) - Thay vào biểu thức cần tính giá trị. Lời giải chi tiết: Phương trình: \(z+\frac{1}{z}=-1\Leftrightarrow {{z}^{2}}+z+1=0\) Ta có: \({{z}_{1}}+{{z}_{2}}=-1;{{z}_{1}}.{{z}_{2}}=1\) Khi đó \(P={{z}_{1}}^{3}+{{z}_{2}}^{3}=\left( {{z}_{1}}+{{z}_{2}} \right)\left( {{z}_{1}}^{2}-{{z}_{1}}{{z}_{2}}+{{z}_{2}}^{2} \right)=\left( {{z}_{1}}+{{z}_{2}} \right)\left[ {{\left( {{z}_{1}}+{{z}_{2}} \right)}^{2}}-3{{z}_{1}}{{z}_{2}} \right]=-1.(1-3)=2\) Chọn C Câu hỏi 14 : Giả sử \({{z}_{1}};{{z}_{2}}\) là hai nghiệm phức của phương trình: \({{z}^{2}}-2z+5=0\) và \(A,B\) là các điểm biểu diễn của \({{z}_{1}};{{z}_{2}}\). Tọa độ trung điểm của đoạn thẳng \(AB\) là:
Đáp án: D Phương pháp giải: - Giải phương trình bậc hai tìm hai nghiệm \({{z}_{1}},{{z}_{2}}\). - Số phức \(z=a+bi\) có điểm biểu diễn trên mặt phẳng phức là \(M\left( a;b \right)\). - Tọa độ trung điểm \(I\) của đoạn thẳng \(AB\) là \(\left(\frac{{{x}_{A}}+{{x}_{B}}}{2};\frac{{{y}_{A}}+{{y}_{B}}}{2} \right)\) Lời giải chi tiết: Phương trình: \({{z}^{2}}-2z+5=0\) Có: \(\Delta '=1-5=-4=4{{i}^{2}}\) \(\Rightarrow \sqrt{\Delta '}=\sqrt{4{{i}^{2}}}=2i\) \(\Rightarrow \) Phương trình có \(2\) nghiệm là: \({{z}_{1}}=1+2i;{{z}_{2}}=1-2i\) Khi đó: \(A\left( 1;2 \right),B(1;-2)\) Tọa độ trung điểm đoạn thẳng \(AB\) là: \(\left( 1;0 \right)\) Chọn D Câu hỏi 15 : Gọi \({{z}_{1}};{{z}_{2}}\) là hai nghiệm phức của phương trình: \({{z}^{2}}+\sqrt{3}z+7=0\). Giá trị của biểu thức \(M={{z}_{1}}^{4}+{{z}_{2}}^{4}\) bằng:
Đáp án: B Phương pháp giải: Định lý vi-et cho phương trình bậc hai: \(\left\{ \begin{array}{l}{z_1} + {z_2} = - \frac{b}{a}\\{z_1}.{z_2} = \frac{c}{a}\end{array} \right.\) Thay vào biểu thức \(M\) để tính giá trị. Lời giải chi tiết: Ta có: \({{z}_{1}}+{{z}_{2}}=-\sqrt{3};{{z}_{1}}.{{z}_{2}}=7\) Khi đó: \(M={{z}_{1}}^{4}+{{z}_{2}}^{4}={{\left( {{z}_{1}}^{2}+{{z}_{2}}^{2} \right)}^{2}}-2{{z}_{1}}^{2}.{{z}_{2}}^{2}\) \(={{\left[ {{\left( {{z}_{1}}+{{z}_{2}} \right)}^{2}}-2{{z}_{1}}.{{z}_{2}} \right]}^{2}}-2{{z}_{1}}^{2}.{{z}_{2}}^{2}\) \(={{\left[ {{\left( -\sqrt{3} \right)}^{2}}-2.7 \right]}^{2}}-{{2.7}^{2}}=23\) Chọn B Câu hỏi 16 : Trong mặt phẳng phức, cho \(3\) điểm \(A,B,C\) lần lượt biểu diễn cho \(3\) số phức\({{z}_{1}}=1+i;{{z}_{2}}={{\left( 1+i \right)}^{2}};{{z}_{3}}=a-i(a\in R)\). Để \(\Delta ABC\) vuông tại \(B\) thì \(a=\)?
Đáp án: C Phương pháp giải: Số phức \(z=a+bi\) có điểm biểu diễn là \(M\left( a;b \right)\). Điều kiện để tam giác \(ABC\) vuông tại \(B\) là \(\overrightarrow{BA}.\overrightarrow{BC}=0\) hoặc \(A{{B}^{2}}+B{{C}^{2}}=A{{C}^{2}}\). Lời giải chi tiết: Ta có: \({{z}_{2}}={{(1+i)}^{2}}=1+2i+{{i}^{2}}=2i\) \(\Rightarrow A(1;1),B(0;2),C(a;-1)\) Khi đó: \(\overrightarrow{AB}=(-1;1)\Rightarrow A{{B}^{2}}=2\) \(\overrightarrow{BC}=(a;-3)\Rightarrow B{{C}^{2}}={{a}^{2}}+9\) \(\overrightarrow{AC}=(a-1;-2)\Rightarrow A{{C}^{2}}={{\left( a-1 \right)}^{2}}+4={{a}^{2}}-2a+5\) Để \(\Delta ABC\) vuông tại \(B\) thì \(A{{C}^{2}}=A{{B}^{2}}+B{{C}^{2}}\) \(\begin{array}{l} \Leftrightarrow {a^2} - 2a + 5 = 2 + {a^2} + 9\\ \Leftrightarrow a = - 3\end{array}\) Chọn C Câu hỏi 17 : Trong tập các số phức, gọi \({{z}_{1}},{{z}_{2}}\) là hai nghiệm của phương trình \({{z}^{2}}-z+\frac{2017}{4}=0\) với \({{z}_{2}}\) có thành phần ảo dương. Cho số phức \(z\) thỏa mãn \(\left| z-{{z}_{1}} \right|=1.\) Giá trị nhỏ nhất của \(P=\left| z-{{z}_{2}} \right|\) là
Đáp án: A Phương pháp giải: Giả sử\(z=a+bi\,\,\left( a,b\in \mathbb{R} \right).\) Giả phương trình ban đầu để tìm được nghiệm \({{z}_{1}},{{z}_{2}}.\) Sử dụng giả thiết để đánh giá cho cho \(b.\) Đưa \({{\left| z-{{z}_{2}} \right|}^{2}}\) về một hàm cho \(b\) và sử dụng ước lượng cho \(b\) ở phần trước để tìm giá trị nhỏ nhất của \(P.\) Lời giải chi tiết: Tính toán ta tìm được hai nghiệm \({{z}_{1}}=\frac{1-i\sqrt{2016}}{2},{{z}_{2}}=\frac{1+i\sqrt{2016}}{2}.\) Giả sử \(z=a+bi\left( a,b\in R \right).\) Từ \(\left| z-{{z}_{1}} \right|=1\) ta suy ra \(\begin{align} & \,\,\,\,\left| \left( a+bi \right)-\frac{1-i\sqrt{2016}}{2} \right|=1\Leftrightarrow 1={{\left( a-\frac{1}{2} \right)}^{2}}+{{\left( b+\frac{\sqrt{2016}}{2} \right)}^{2}}\Rightarrow {{\left( b+\frac{\sqrt{2016}}{2} \right)}^{2}}\le 1 \\ & \Rightarrow -1-\frac{\sqrt{2016}}{2}\le b\le 1-\frac{\sqrt{2016}}{2}\,\,\left( 1 \right). \\ \end{align}\) Áp dụng \(\left( 1 \right)\) ta nhận được \(\begin{array}{l} Do đó giá trị nhỏ nhất của \(P=\left| z-{{z}_{2}} \right|\) là \(\sqrt{2016}-1.\) Đạt được khi và chỉ khi \(b=1-\frac{\sqrt{2016}}{2},a=\frac{1}{2}.\) Chọn đáp án A. Câu hỏi 18 : Trong tập các số phức, cho phương trình \({{z}^{2}}-6z+m=0,\,\,m\in \mathbb{R}\,\,\left( 1 \right).\) Gọi \({{m}_{0}}\) là một giá trị của \(m\) đẻ phương trình \(\left( 1 \right)\) có hai nghiệm phân biệt \({{z}_{1}},{{z}_{2}}\) thỏa mãn \({{z}_{1}}.\overline{{{z}_{1}}}={{z}_{2}}.\overline{{{z}_{2}}.}\) Hỏi trong khoảng \(\left( 0;20 \right)\) có bao nhiêu giá trị \({{m}_{0}}\in \mathbb{N}?\)
Đáp án: D Phương pháp giải: Biện luận để tìm trực tiếp nghiệm \({{z}_{1}},{{z}_{2}}.\) Sử dụng giả thiết để tìm ra giá trị \({{m}_{0}}.\) Lời giải chi tiết: Viết lại phương trình đã cho thành \({{\left( z-3 \right)}^{2}}=9-{{m}_{0}}.\) Nếu \({{m}_{0}}=9\Rightarrow z=3.\) Hay phương trình chỉ có một nghiệm. (Loại) Nếu \({{m}_{0}}<9\) thì phương trình đã cho có hai nghiệm thực \({{z}_{1}}=3-\sqrt{9-{{m}_{0}}},{{z}_{2}}=3+\sqrt{9-{{m}_{0}}}.\) Do \(\begin{array}{l}{z_1}.\overline {{z_1}} = {z_2}.\overline {{z_2}} \Leftrightarrow {\left| {{z_1}} \right|^2} = {\left| {{z_2}} \right|^2} \Leftrightarrow {\left( {3 - \sqrt {9 - {m_0}} } \right)^2} = {\left( {3 + \sqrt {9 - {m_0}} } \right)^2}\\ \Leftrightarrow \left[ \begin{array}{l}3 - \sqrt {9 - {m_0}} = 3 + \sqrt {9 - {m_0}} \\3 - \sqrt {9 - {m_0}} = - 3 - \sqrt {9 - {m_0}} \,\,\,\left( {VN} \right)\end{array} \right. \Leftrightarrow \sqrt {9 - {m_0}} = 0 \Leftrightarrow {m_0} = 9\,\,\left( {ktm} \right)\end{array}\) Nếu \({{m}_{0}}>9\) thì phương trình đã cho có hai nghiệm phức liên hợp là \({{z}_{1}}=3-i\sqrt{{{m}_{0}}-9},{{z}_{2}}=3+i\sqrt{{{m}_{0}}-9}.\) Khi đó \({{z}_{1}}.\overline{{{z}_{1}}}={{z}_{2}}.\overline{{{z}_{2}}}={{3}^{2}}+{{\left( \sqrt{{{m}_{0}}-9} \right)}^{2}}\) Do đó \({{m}_{0}}>9\)thỏa mãn yêu cầu bài toán. Do bài toán đòi hỏi \({{m}_{0}}\in \left( 0;20 \right)\) nên \({{m}_{0}}\in \left\{ 10;11;....;19 \right\}.\) Vậy có \(10\) giá trị thỏa mãn. Chọn đáp án D. Câu hỏi 19 : Tập nghiệm của phương trình \({z^4} - 2{z^3} - {z^2} - 2z + 1 = 0\) là :
Đáp án: D Lời giải chi tiết: \({z^4} - 2{z^3} - {z^2} - 2z + 1 = 0\) Vì \(z{\text{ }} = {\text{ }}0\) không là nghiệm của phương trình nên chia cả 2 vế của phương trình cho \({z^2} \ne 0\) , ta được: \({z^2} - 2{\text{z}} - 1 - \dfrac{2}{z} + \dfrac{1}{{{z^2}}} = 0 \Leftrightarrow \left( {{z^2} + \dfrac{1}{{{z^2}}}} \right) - 2\left( {z + \dfrac{1}{z}} \right) - 1 = 0\) \( \Leftrightarrow {\left( {z + \dfrac{1}{z}} \right)^2} - 2\left( {z + \dfrac{1}{z}} \right) - 3 = 0\) Đặt \(t = z + \dfrac{1}{z}\) phương trình trở thành: \({t^2} - 2t - 3 = 0 \Leftrightarrow \left[ \begin{array}{l}t = - 1\\t = 3\end{array} \right.\) +) Với \(t = - 1 \Leftrightarrow z + \dfrac{1}{z} = - 1 \Leftrightarrow {z^2} + z + 1 = 0 \Rightarrow z = \dfrac{{ - 1 \pm i\sqrt 3 }}{2}\) +) Với \(t = 3 \Leftrightarrow z + \dfrac{1}{z} = 3 \Leftrightarrow {z^2} - 3z + 1 = 0 \Rightarrow z = \dfrac{{3 \pm \sqrt 5 }}{2}\) Vậy tập nghiệm của phương trình là: \(\left\{ {\dfrac{{ - 1 \pm i\sqrt 3 }}{2};\dfrac{{3 \pm \sqrt 5 }}{2}} \right\}\) Chọn D Câu hỏi 20 : Phương trình : \({z^6}-9{z^3} + 8 = 0\) có bao nhiêu nghiệm phân biệt trên tập số phức?
Đáp án: D Lời giải chi tiết: \(\begin{array}{l}{z^6}-9{z^3} + 8 = 0 \Leftrightarrow \left( {{z^3} - 1} \right)\left( {{z^3} - 8} \right) = 0\\ \Leftrightarrow \left( {z - 1} \right)\left( {{z^2} + z + 1} \right)\left( {z - 2} \right)\left( {{z^2} + 2{\rm{z}} + 4} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}z = 1\\z = 2\\{z^2} + z + 1 = 0\\{z^2} + 2{\rm{z}} + 4 = 0\end{array} \right.\end{array}\) +) Phương trình: \({z^2} + {\text{ }}z + 1 = 0\) có \(\Delta = 1-4 = - 3 = 3{i^2} \Rightarrow z = \dfrac{{ - 1 \pm i\sqrt 3 }}{2}\) +) Phương trình: \({z^2} + 2z + 4 = 0\) có \(\Delta ' = 1 - 4 = - 3 = 3{i^2} \Rightarrow z = - 1 \pm i\sqrt 3 \) Vậy phương trình có 6 nghiệm phân biệt. Chọn D Câu hỏi 21 : Cho phương trình : \({z^3} - \left( {2i - 1} \right){z^2} + (3 - 2i)z + 3 = 0\) Trong số các nhận xét: 1. Phương trình chỉ có 1 nghiệm thuộc tập hợp số thực 2. Phương trình chỉ có 2 nghiệm thuộc tập hợp số phức 3. Phương trình có 2 nghiệm có phần thực bằng 0 4. Phương trình có 2 nghiệm là số thuần ảo 5. Phương trình có 3 nghiệm, trong đó 2 nghiệm là số phức liên hợp Số nhận xét sai là:
Đáp án: B Lời giải chi tiết: \(\begin{array}{l}{z^3} - \left( {2i - 1} \right){z^2} + (3 - 2i)z + 3 = 0\\ \Leftrightarrow \left( {z + 1} \right)\left( {{z^2} - 2iz + 3} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}z = - 1\\{z^2} - 2iz + 3 = 0\end{array} \right.\end{array}\) +) Phương trình: \({z^2}-2iz + 3 = 0\) có \(\Delta ' = {i^2} - 3 = - 4 = 4{i^2} \Rightarrow z = 3i;z = - i\) Do đó các nhận xét 1; 3; 4 là đúng. Nhận xét 2 sai vì cả 3 nghiệm đều thuộc tập số phức. Nhận xét 5 sai vì \(3i\) và \( - i\) không phải là hai số phức liên hợp. Chọn B Câu hỏi 22 : Số nghiệm phân biệt của phương trình \({z^3} + (1 - 2i){z^2} + (1 - i)z - 2i = 0\) trên tập số phức là:
Đáp án: D Lời giải chi tiết: \(\begin{array}{l}{z^3} + (1 - 2i){z^2} + (1 - i)z - 2i = 0\\ \Leftrightarrow \left( {z - i} \right)\left[ {{z^2} + \left( {1 - i} \right)z + 2} \right] = 0\\ \Leftrightarrow \left[ \begin{array}{l}z = i\\{z^2} + (1 - i)z + 2 = 0\end{array} \right.\end{array}\) +) Giải phương trình \({z^2} + \left( {1-i} \right)z + 2 = 0\) ta tìm được 2 nghiệm phức khác \(i\) Vậy phương trình có 3 nghiệm phức phân biệt. Chọn D Câu hỏi 23 : Gọi \({z_1};{z_2};{z_3};{z_4}\) là 4 nghiệm của phương trình: \({z^4} - {z^3} - 2{z^2} + 6z - 4 = 0\) trên tập số phức. Khi đó tổng \(S = \dfrac{1}{{{z_1}^2}} + \dfrac{1}{{{z_2}^2}} + \dfrac{1}{{{z_3}^2}} + \dfrac{1}{{{z_4}^2}}\) bằng:
Đáp án: A Lời giải chi tiết: \(\begin{array}{l}{z^4} - {z^3} - 2{z^2} + 6z - 4 = 0\\ \Leftrightarrow \left( {z - 1} \right)(z + 2)({z^2} - 2z + 2) = 0\\ \Leftrightarrow \left[ \begin{array}{l}z - 1 = 0\\z + 2 = 0\\{z^2} - 2z + 2 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}z = 1\\z = - 2\\{z^2} - 2z + 2 = 0\end{array} \right.\end{array}\) +) Phương trình: \({z^2}-2z + 2 = 0\) có \(\Delta ' = 1 - 2 = - 1 = {i^2}\) \( \Rightarrow z = 1 + {\text{ }}i;z = 1-i.\) Giả sử: \({z_1} = 1;{z_2} = - 2;{z_3} = 1 + i;{z_4} = 1 - i\) \( \Rightarrow S = \dfrac{1}{{{z_1}^2}} + \dfrac{1}{{{z_2}^2}} + \dfrac{1}{{{z_3}^2}} + \dfrac{1}{{{z_4}^2}} = 1 + \dfrac{1}{4} + \dfrac{1}{{{{(1 + i)}^2}}} + \dfrac{1}{{{{(1 - i)}^2}}} = 1 + \dfrac{1}{4} + \dfrac{1}{{2i}} + \dfrac{1}{{ - 2i}} = \dfrac{5}{4}\) Chọn A Câu hỏi 24 : Tìm tất cả các nghiệm của phương trình: \({z^4} - 4{z^3} + 14{z^2} - 36z + 45 = 0\)
Đáp án: C Lời giải chi tiết: \(\begin{array}{l}{z^4} - 4{z^3} + 14{z^2} - 36z + 45 = 0\\ \Leftrightarrow \left( {{z^2} + 9} \right)({z^2} - 4{\rm{z}} + 5) = 0\\ \Leftrightarrow \left[ \begin{array}{l}{z^2} + 9 = 0\\{z^2} - 4{\rm{z}} + 5 = 0\end{array} \right.\end{array}\) +) Phương trình: \({z^2} + 9 = 0 \Leftrightarrow {z^2} = - 9 = 9{i^2} \Leftrightarrow z = \pm 3i\) +) Phương trình: \({z^2}-4z + 5 = 0\) có \(\Delta ' = 4 - 5 = - 1 = {i^2} \Rightarrow z = 2 \pm i\) Vậy tập nghiệm của phương trình là: \(\left\{ {2 + i;2 - i;3i; - 3i} \right\}\) Chọn C Câu hỏi 25 : Cho phương trình \({z^3} + a{z^2} + bz + c = 0\left( {a,b,c \in R;{\text{ }}a \ne 0} \right)\). Nếu \(z = 1 + i\) và \(z = 2\) là 2 nghiệm của phương trình thì \(a,b,c\) bằng:
Đáp án: A Lời giải chi tiết: Vì \(z = 1 + i\) là nghiệm của phương trình nên ta có: \(\begin{array}{l}{\left( {1 + i} \right)^3} + a{\left( {1 + i} \right)^2} + b\left( {1 + i} \right) + c = 0\\ \Leftrightarrow 1 + 3i + 3{i^2} + {i^3} + a(1 + 2i + {i^2}) + b + bi + c = 0\\ \Leftrightarrow 1 + 3i - 3 - i + a + 2ai - a + b + bi + c = 0\\ \Leftrightarrow \left( {b + c - 2} \right) + \left( {2a + b + 2} \right)i = 0\\ \Leftrightarrow \left\{ \begin{array}{l}2a + b + 2 = 0\\b + c - 2 = 0\end{array} \right.{\rm{ }}\left( 1 \right)\end{array}\) Vì \(z = 2\) là nghiệm của phương trình nên: \({2^3} + a{.2^2} + b.2 + c = 0 \Leftrightarrow 4a + 2b + c + 8 = 0{\text{ }}\left( 2 \right)\) Từ (1) và (2) ta có hệ phương trình: \( \Leftrightarrow \left\{ \begin{array}{l}2a + b = - 2\\b + c = 2\\4a + 2b + c = - 8\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = - 4\\b = 6\\c = - 4\end{array} \right.\) Chọn A Câu hỏi 26 : Cho hai số thực b ;c (c > 0). Kí hiệu A, B là hai điểm của mặt phẳng phức biểu diễn hai nghiệm của phương trình \({{z}^{2}}+2bz+c=0\), tìm điều kiện của b và c sao cho tam giác OAB là tam giác vuông (với O là gốc tọa độ).
Đáp án: C Phương pháp giải: +) Nếu \(z\) là một nghiệm phức của phương trình bậc hai thì \(\overline{z}\) cũng là nghiệm của phương trình bậc hai đó. +) Tìm hai nghiệm phức của phương trình bậc hai đã cho. +) Xác định các điểm biểu diễn A, B. +) \(\Delta OAB\) vuông tại \(O\Rightarrow \overrightarrow{OA}.\overrightarrow{OB}=0\). Lời giải chi tiết: Ta có \(\Delta '={{b}^{2}}-c<0\Leftrightarrow {{b}^{2}}<C\) Gọi \(z=x+yi\) la 1 nghiệm phức của phương trình \({{z}^{2}}+2bz+c=0\Rightarrow \overline{z}=x-yi\) cũng là một nghiệm của phương trình. Ta có \(\begin{array}{l}z + \overline z = 2x = - 2b \Leftrightarrow x = - b\\z.\overline z = {x^2} + {y^2} = c \Leftrightarrow y = \pm \sqrt {c - {b^2}} \\ \Rightarrow \left\{ \begin{array}{l}z = - b + \sqrt {c - {b^2}} i \Rightarrow A\left( { - b;\sqrt {c - {b^2}} } \right)\\\overline z = - b - \sqrt {c - {b^2}} i \Rightarrow B\left( { - b; - \sqrt {c - {b^2}} } \right)\end{array} \right.\\OA \bot OB \Rightarrow \overrightarrow {OA} .\overrightarrow {OB} = 0 \Leftrightarrow {b^2} - \left( {c - {b^2}} \right) = 0 \Leftrightarrow 2{b^2} - c = 0 \Leftrightarrow c = 2{b^2}\end{array}\) Chọn C. Câu hỏi 27 : Gọi \({z_1},{z_2},{z_3},{z_4}\) là các nghiệm phức của phương trình \({z^4} + {z^2} - 6 = 0\). Tính \(T = z_1^2 + z_2^2 + z_3^2 + z_4^2\).
Đáp án: D Phương pháp giải: Giải phương trình phức và kết luận. Lời giải chi tiết: Ta có: \({z^4} + {z^2} - 6 = 0 \Leftrightarrow \left[ \begin{array}{l}{z^2} = - 3\\{z^2} = 2\end{array} \right.\) \({z_1},{z_2},{z_3},{z_4}\) là các nghiệm phức của phương trình \({z^4} + {z^2} - 6 = 0 \Rightarrow z_1^2 = z_2^2 = - 3;\,\,\,z_3^2 = z_4^2 = 2\) \(T = z_1^2 + z_2^2 + z_3^2 + z_4^2 = - 3 - 3 + 2 + 2 = - 2\). Chọn: D Câu hỏi 28 : Tham số phức \(m\) bằng bao nhiêu để phương trình: \({{z}^{2}}+mz+3i=0\) có tổng bình phương các nghiệm bằng \(8\)
Đáp án: C Phương pháp giải: - Áp dụng định lý Vi-et cho phương trình bậc hai: \(\left\{ \begin{array}{l}{z_1} + {z_2} = - \frac{b}{a}\\{z_1}.{z_2} = \frac{c}{a}\end{array} \right.\) - Thay vào biểu thức bài cho để tìm . Lời giải chi tiết: Ta có: \({{z}_{1}}+{{z}_{2}}=-m;{{z}_{1}}.{{z}_{2}}=3i\) \(\Rightarrow {{z}_{1}}^{2}+{{z}_{2}}^{2}=8\Leftrightarrow {{\left( {{z}_{1}}+{{z}_{2}} \right)}^{2}}-2{{z}_{1}}.{{z}_{2}}=8\) \(\begin{array}{l} \Leftrightarrow {m^2} - 2.3i = 8\\ \Leftrightarrow {m^2} = 8 + 6i = {\left( {3 + i} \right)^2}\\ \Leftrightarrow \left[ \begin{array}{l}m = 3 + i\\m = - 3 - i\end{array} \right.\end{array}\) Chọn C Câu hỏi 29 : Gọi \({{z}_{1}}\) là nghiệm phức có phần ảo âm của phương trình: \({{z}^{2}}+4z+20=0\). Khi đó giá trị biểu thức \(A={{\left| {{z}_{1}} \right|}^{2}}+2\left( {{z}_{1}}^{2}+{{z}_{2}}^{2} \right)\) bằng
Đáp án: A Phương pháp giải: - Giải phương trình bậc hai tìm hai nghiệm. - Kết hợp điều kiện để loại nghiệm. - Thay nghiệm thỏa mãn vào biểu thức cần tính giá trị. Lời giải chi tiết: Phương trình : \({{z}^{2}}+4z+20=0\) Có: \(\Delta '=4-20=-16=16{{i}^{2}}\) \(\Rightarrow \sqrt{\Delta '}=\sqrt{16{{i}^{2}}}=4i\) Phương trình có \(2\) nghiệm là: \({{z}_{1}}=-2-4i;{{z}_{2}}=-2+4i\) Khi đó: \({{\left| {{z}_{1}} \right|}^{2}}={{(-2)}^{2}}+{{\left( -4 \right)}^{2}}=20\) và \({{z}_{1}}+{{z}_{2}}=-4;{{z}_{1}}.{{z}_{2}}=20\) \(\Rightarrow \left( {{z}_{1}}^{2}+{{z}_{2}}^{2} \right)={{\left( {{z}_{1}}+{{z}_{2}} \right)}^{2}}-2{{z}_{1}}.{{z}_{2}}={{\left( -4 \right)}^{2}}-2.20=-24\) Vậy \(A={{\left| {{z}_{1}} \right|}^{2}}+2\left( {{z}_{1}}^{2}+{{z}_{2}}^{2} \right)=20+2(-24)=-28\) Chọn A Câu hỏi 30 : Cho số phức \(z\)và gọi \({z_1},{z_2}\) là hai nghiệm phức của phương trình \({z^2} + 8i = 0\) (\({z_1}\) có phần thực dương). Giá trị nhỏ nhất của biểu thức \(P = \left| {z - {z_1}} \right| + \left| {{z_2} - z} \right| + \left| {\overline z + 2{z_1} + \dfrac{{{z_2}}}{2}} \right|\) được viết dưới dạng \(m\sqrt n + p\sqrt {q\,} \)(trong đó \(n,p \in \mathbb{N};\;\;m,q\)là các số nguyên tố). Tổng \(m + n + p + q\) bằng
Đáp án: B Phương pháp giải: Lời giải chi tiết: Đặt \(z=a+bi\Rightarrow \overline{z}=a-bi\,\,\left( a;b\in \mathbb{R} \right)\). \(\Rightarrow P=\sqrt{{{\left( a-2 \right)}^{2}}+{{\left( b+2 \right)}^{2}}}+\sqrt{{{\left( a+2 \right)}^{2}}+{{\left( b-2 \right)}^{2}}}+\sqrt{{{\left( a+3 \right)}^{2}}+{{\left( b+3 \right)}^{2}}}=f\left( a;b \right)\). Ta có \(f\left( a;b \right)=f\left( b;a \right)\,\,\forall a,b\), ta dự đoán dấu "=" xảy ra \(\Leftrightarrow a=b=k\). \(\sqrt{{{\left( a-2 \right)}^{2}}+{{\left( b+2 \right)}^{2}}}\ge \frac{1}{\sqrt{{{m}^{2}}+{{n}^{2}}}}\sqrt{\left( {{m}^{2}}+{{n}^{2}} \right)\left[ {{\left( a-2 \right)}^{2}}+{{\left( b+2 \right)}^{2}} \right]}\ge \frac{m\left( a-2 \right)+n\left( b+2 \right)}{\sqrt{{{m}^{2}}+{{n}^{2}}}}\). Dấu "=" xảy ra \(\Leftrightarrow \left\{ \begin{align}\frac{m}{a-2}=\frac{n}{b+2} \\ a=b=k \\ \end{align} \right.\). Chọn \(m=k-2,\,\,n=k+2\). \(\Rightarrow \sqrt{{{\left( a-2 \right)}^{2}}+{{\left( b+2 \right)}^{2}}}\ge \frac{\left( k-2 \right)\left( a-2 \right)+\left( k+2 \right)\left( b+2 \right)}{\sqrt{2{{k}^{2}}+8}}=\frac{k\left( a+b \right)-2a+2b+8}{\sqrt{2{{k}^{2}}+8}}\) Tương tự : \(\begin{align}\sqrt{{{\left( a+2 \right)}^{2}}+{{\left( b-2 \right)}^{2}}}\ge \frac{k\left( a+b \right)+2a-2b+8}{\sqrt{2{{k}^{2}}+8}} \\ \sqrt{{{\left( a+3 \right)}^{2}}+{{\left( b+3 \right)}^{2}}}\ge \frac{1}{\sqrt{2}}\sqrt{{{\left[ 1\left( a+3 \right)+1\left( b+3 \right) \right]}^{2}}}=\frac{a+b+6}{\sqrt{2}} \\ \end{align}\) Cộng vế với vế ta có: \(P\ge \frac{2k\left( a+b \right)}{\sqrt{2{{k}^{2}}+8}}+\frac{16}{\sqrt{2{{k}^{2}}+8}}+\frac{a+b}{\sqrt{2}}+\frac{6}{\sqrt{2}}\) cần chọn số \(k\) sao cho \(\frac{2k}{\sqrt{2{{k}^{2}}+8}}+\frac{1}{\sqrt{2}}=0\Leftrightarrow k=-\frac{2}{\sqrt{3}}\). Khi đó \(P\ge 2\sqrt{6}+3\sqrt{2}\). Vậy \(m=q=2;\,\,n=6;\,\,p=3 \,\,\Rightarrow m+n+p+q=2+6+3+2=13\). Chọn B. (Sưu tầm Group FB: Strong Team Toán VD – VDC). Quảng cáo
|