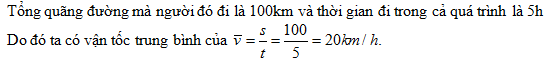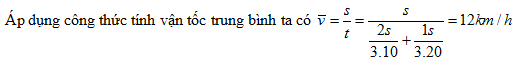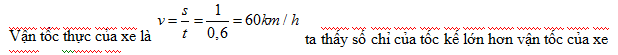30 bài tập Chuyển động thẳng đều mức độ vận dụngLàm bàiQuảng cáo
Câu hỏi 1 : Phương trình chuyển động thẳng đều của một chất điểm có dạng: x = 4t – 10. (x: km, t: h). Quãng đường đi được của chất điểm sau 2h là:
Đáp án: D Lời giải chi tiết: Vì phương trình tọa độ của vật có dạng x = 4t – 10. (x: km, t: h) nên phương trình chuyển động của vật là s = 4t. Do đó sau 2h quãng đường vật đi được là s = 2.4 = 8m Câu hỏi 2 : Một vật chuyển động thẳng đều đi được 45 m trong thời gian 5 giây. Hỏi vận tốc của vật là bao nhiêu?
Đáp án: C Lời giải chi tiết: Vì vật chuyển động thẳng đều nên ta có : v=s/t = 45/5 = 9m/s Câu hỏi 3 : Một hành khách đi từ A đến B cách nhau 50 km trong 2 giờ. Nghỉ tại B 1 giờ và trở về A trong 2 giờ. Tốc độ trung bình của người đó trong suốt đường đi và về là
Đáp án: B Lời giải chi tiết: Câu hỏi 4 : Một người đi xe đạp trên 2/3 đoạn đường đầu với vận tốc trung bình 10km/h và 1/3 đoạn đường sau với vận tốc trung bình 20km/h. Vận tốc trung bình của người đi xe đạp trên cả quãng đường là
Đáp án: A Lời giải chi tiết: Câu hỏi 5 : Lúc 6h một ô tô chuyển động thẳng đều từ A đến B với vận tốc 30 km/h. Chọn gốc tọa độ tại A, chiều dương từ A đến B, gốc thời gian lúc 6h. Phương trình chuyển động của ô tô là:
Đáp án: C Lời giải chi tiết: Đáp án C Lúc 6h một ô tô chuyển động thẳng đều từ A đến B với vận tốc 30 km/h. Chọn gốc tọa độ tại A, chiều dương từ A đến B, gốc thời gian lúc 6h. Phương trình chuyển động của ô tô là: x = 30t ( km-h); Câu hỏi 6 : Phương trình chuyển động của một chất điểm trên trục Ox có dạng: x = 5+ 60t (x: km, t: h) Chất điểm đó xuất phát từ điểm nào và chuyển động với vận tốc bằng bao nhiêu?
Đáp án: D Lời giải chi tiết: Phương trình chuyển động của một chất điểm trên trục Ox có dạng: x = 5+ 60t (x: km, t: h) Chất điểm đó xuất phát từ điểm M, cách O là 5km, với vận tốc 60 km/h Câu hỏi 7 : Tốc kế của một ôtô đang chạy chỉ 70km/h tại thời điểm t. Để kiểm tra xem đồng hồ tốc kế đó chỉ có đúng không, người lái xe giữ nguyên vận tốc, một người hành khách trên xe nhìn đồng hồ và thấy xe chạy qua hai cột cây số bên đường cách nhau 1 km trong thời gian 1min. Số chỉ của tốc kế
Đáp án: C Lời giải chi tiết: Câu hỏi 8 : Một ôtô chạy trên một đường thẳng, lần lượt đi qua 3 điểm A, B, C cách đều nhau một khoảng 12km. Xe đi đoạn AB hết 20min, đoạn BC hết 30min. Vận tốc trung bình trên
Đáp án: A Lời giải chi tiết: Một ôtô chạy trên một đường thẳng, lần lượt đi qua 3 điểm A, B, C cách đều nhau một khoảng 12km. Xe đi đoạn AB hết 20min, đoạn BC hết 30min. Vận tốc trung bình trên đoạn AB lớn hơn trên đoạn BC Câu hỏi 9 : Hai thành phố A và B cách nhau 250km. Lúc 6h sáng, 2 ô tô khởi hành từ hai thành phố đó hướng về nhau. Xe từ A có vận tốc v1 = 60km/h, xe kia có vận tốc v2 = 40 km/h. Hỏi 2 ô tô sẽ gặp nhau lúc mấy giờ và vị trí này cách B bao nhiêu km?
Đáp án: D Lời giải chi tiết: Câu hỏi 10 : Cùng một lúc tại hai điểm A và B cách nhau 10km có hai ô tô chạy cùng chiều nhau trên một đường thẳng. Vận tốc của ô tô chạy từ A là 54km/h và của ô tô chạy từ B là 48km/h. Chọn A làm mốc, chọn thời điểm xuất phát của hai xe ô tô làm mốc thời gian và chọn chiều chuyển động của hai ô tô làm chiều dương. Phương trình chuyển động của các ô tô trên như thế nào? Chọn câu trả lời đúng:
Đáp án: D Lời giải chi tiết: Ô tô chạy từ A : xA = 54t ; ô tô chạy từ B : xB = 48t + 10 Câu hỏi 11 : Một ô tô chuyển động thẳng đều với vận tốc bằng 80 km/h. Bến xe nằm ở đầu đoạn đường và xe ô tô xuất phát từ một địa điểm cách bến xe 3km. Chọn bến xe làm vật mốc, thời điểm ô tô xuất phát làm mốc thời gian và chọn chiều chuyển động của ô tô làm chiều dương. Phương trình chuyển động của xe ô tô trên đoạn đường thẳng này là:
Đáp án: A Lời giải chi tiết: Gọi bến xe là mốc Phương trình chuyển động của xe là x = x0 + v.t do vật cách bến xe 3 km và có vận tốc 80 km/h nên ta có phương trình chuyển động của oto này là x = 3 +80t. Câu hỏi 12 : Hai xe chạy ngược chiều đến gặp nhau, cùng khởi hành một lúc từ hai địa điểm A và B cách nhau 120km. Vận tốc của xe đi từ A là 40km/h, của xe đi từ B là 20km/h. Phương trình chuyển động của hai xe khi chọn trục toạ độ 0x hướng từ A sang B, gốc 0ºA là
Đáp án: B Lời giải chi tiết: Hai xe chạy ngược chiều đến gặp nhau, cùng khởi hành một lúc từ hai địa điểm A và B cách nhau 120km. Vận tốc của xe đi từ A là 40km/h, của xe đi từ B là 20km/h. Phương trình chuyển động của hai xe khi chọn trục toạ độ 0x hướng từ A sang B, gốc 0ºA là xA = 40t(km); xB = 120 - 20t(km) Câu hỏi 13 : Hai ôtô xuất phát cùng một lúc, xe 1 xuất phát từ A chạy về B, xe 2 xuất phát từ B cùng chiều xe 1, AB = 20 km. Vận tốc xe 1 là 50 km/h, xe B là 30 km/h. Hỏi sau bao lâu xe 1 gặp xe 2
Đáp án: A Phương pháp giải: Phương pháp : Áp dụng điều kiện hai xe gặp nhau khi \({x_1}\; = {x_2}\;\) Lời giải chi tiết: Cách giải: Chọn gốc toạ độ tại vị trí tại A, gốc thời gian lúc 2 xe xuất phát. Phương trình chuyển động có dạng: x1 = 50t ; x2 = 20 + 30t Khi hai xe đuổi kịp nhau: x1 = x2 suy ra t = 1h Chọn A Câu hỏi 14 : Lúc 7 giờ, một người ở A chuyển động thẳng đều với v = 36 km/h đuổi theo người ở B đang chuyển động với v = 5 m/s. Biết AB = 18 km. Viết phương trình chuyển động của 2 người. Lúc mấy giờ và ở đâu 2 người đuổi kịp nhau
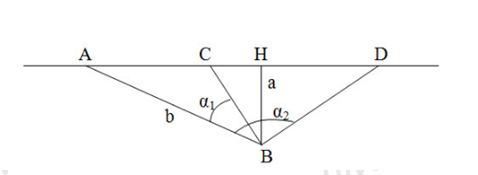
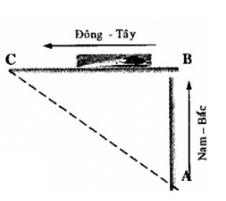
Đáp án: C Phương pháp giải: Phương pháp : Áp dụng điều kiện hai xe gặp nhau khi \({x_1}\; = {x_2}\;\) Lời giải chi tiết: Chọn gốc toạ độ tại A, gốc thời gian lúc 7 giờ. Ptcđ có dạng: \({x_A}\; = 36t{\rm{ }};{x_B}\; = {x_0}\; + {\rm{ }}{v_B}.t = 18 + 18t\) Khi hai xe gặp nhau: \({x_1}\; = {x_2}\;\)suy ra t = 1h, hai người gặp nhau lúc 8h. Vậy \({x_A}\; = {x_B}\; = 36km\) Chọn C Câu hỏi 15 : Xe bus chuyển động thẳng đều trên đường với \({v_1} = 16m/s\). Một hành khách đứng cách đường một đoạn \(a = 60m\), người này nhìn thấy xe bus vào thời điểm xe cách người một khoảng \(b = 400m\). Nếu muốn gặp xe với vận tốc nhỏ nhất thì người này phải chạy với vận tốc là bao nhiêu?
Đáp án: C Phương pháp giải: Phương pháp : Áp dụng điều kiện hai xe gặp nhau khi \({x_1}\; = {x_2}\;\) Lời giải chi tiết: Hướng dẫn giải: Nếu muốn vận tốc là nhỏ nhất => quãng đường đi là nhỏ nhất => người đó đi theo hướng BH Từ hình ta có: \(AH = \sqrt {{b^2} - {a^2}} = \sqrt {{{400}^2} - {{60}^2}} \approx 395.5(m)\) Ta có: \(\frac{{BH}}{{{v_{\min }}}} = \frac{{AH}}{{{v_1}}} \to {v_{\min }} = \frac{{BH}}{{AH}}.{v_1} = \frac{{60}}{{395,5}}.16 = 2,4(m/s)\) Chọn C Câu hỏi 16 : Một ca-nô rời bến chuyển động thẳng đều. Đầu tiên, ca-nô chạy theo hướng nam bắc trong thời gian 2 phút 40 giây rồi tức thì rẽ sang hướng đông tây và chạy thêm 2 phút với vận tốc như trước và dừng lại. Khoảng cách từ nơi xuất phát tới nơi dừng lại là 1km. Vận tôc của ca-nô là:
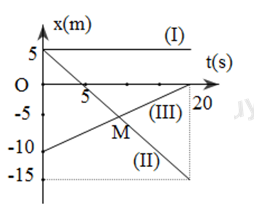
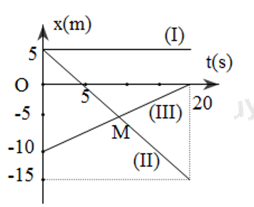
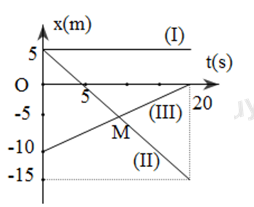
Đáp án: D Phương pháp giải: Phương pháp: Vận dụng biểu thức: \(v = \frac{s}{t}\) Lời giải chi tiết: Hướng dẫn giải: Đổi đơn vị, ta có: 2 phút 40 giây = 160s; 2phút = 120s 1km = 1000m Gọi A - điểm xuất phát; B- điểm bắt đầu rẽ, C- điểm dừng lại của ca-nô Ta có: \(\begin{array}{*{20}{l}}{A{C^2} = A{B^2} + B{C^2} = {{\left( {v{t_1}} \right)}^2} + {{\left( {v{t_2}} \right)}^2}}\\{ \to v = \frac{{AC}}{{\sqrt {t_1^2 + t_2^2} }} = \frac{{1000}}{{\sqrt {{{160}^2} + {{120}^2}} }} = 5m/s = 18km/h}\end{array}\) Chọn D Câu hỏi 17 : Đồ thị của 3 vật (I), (II), (III) được thể hiện trên hình vẽ: Phương trình chuyển động của vật (I) có dạng như thế nào?
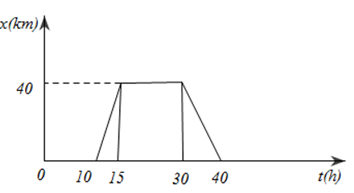
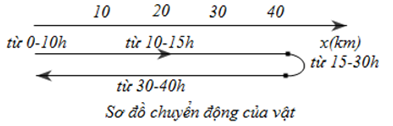
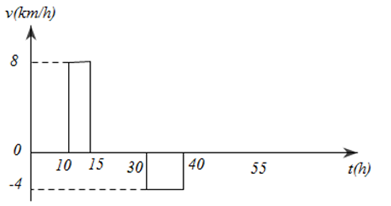
Đáp án: C Phương pháp giải: Phương pháp : Khi vật đang đứng yên thì tọa độ của nó không đổi theo thời gian Lời giải chi tiết: Cách giải : Từ độ thị ta thấy tọa độ của vật (I) không thay đổi theo thời gian => vật đang đứng yên vật phương trình tọa độ của xe (I): \({x_1}\; = 5{\rm{ }}m/s\) Chọn C Câu hỏi 18 : Hãy mô tả chuyển động của một vật có đồ thị vị trí- thời gian ở như hình vẽ và đồ thị vận tốc- thời gian tương ứng của vật. Phương pháp giải: Lời giải chi tiết: + Trong khoảng thời gian từ 0h đến 10h: Tọa độ x = 0, vật đứng yên tại gốc toạ độ O. + Trong khoảng thời gian từ 10h đến 15h: Vật chuyển động từ gốc O đến vị trí có x = 40 km, tức là theo chiều dương, với vận tốc trung bình: \({v_{tb}} = \frac{{{x_2} - {x_1}}}{{{t_2} - {t_1}}} = \frac{{40 - 0}}{{15 - 0}} = 8km/h\) + Trong khoảng thời gian từ 15h đến 30h : Toạ độ luôn là x = 40 km, vật đứng yên tại vị trí này. + Trong khoảng thời gian từ 30h đến 40h: Vật chuyển động từ vị trí có x = 40 km đến vị trí có x = 0 (theo chiều âm),với vận tốc trung bình là:\({v_{tb}} = \frac{{0 - 40}}{{40 - 30}} = - 4km/h\) + Từ 40h trở đi: Vật đứng yên tại gốc O. Ta có sơ đồ chuyển động: Và nếu chỉ để ý sự biến thiên của vận tốc theo thời gian, ta vẽ được đồ thị vận tốc-thời gian: Câu hỏi 19 : Vật chuyển động thẳng đều có đồ thị tọa độ-thời gian như hình vẽ. Phương trình chuyển động của vật có dạng như thế nào?
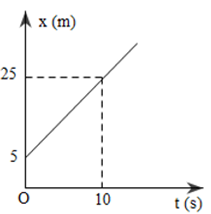
Phương pháp giải: Lời giải chi tiết: Ta có: \(\left\{ \matrix{ Do đó phương trình chuyển động của vật là: x = x0 + vt = 5 + 2t Câu hỏi 20 : Lúc 7h một oto chuyển động từ A đến B với vận tốc 80km/h. Cùng lúc một oto chuyển động từ B về A với vận tốc 80km/h. Biết khoảng cách từ A đến B là 200km, coi chuyển động của hai oto là chuyển động thẳng đều . Hai xe gặp nhau tại vị trí cách A là bao nhiêu? Khi đó đồng hồ chỉ mấy h?
Đáp án: D Phương pháp giải: Phương pháp: + Viết phương trình chuyển động của 2 xe + Giải phương trình : x1 = x2 (c3) Lời giải chi tiết: Hướng dẫn giải: Chọn chiều (+) là chiều từ A đến B, gốc thời gian là lúc 7h, gốc tọa độ tại điểm A Phương trình chuyển động của 2 oto là: \(\begin{array}{*{20}{l}}{{x_1} = {x_{01}} + 80t}\\{{x_2} = {x_{02}} - 80t}\end{array}\) Tại thời điểm ban đầu: \({t_0} = 0\) (lúc đồng hồ chỉ 7h) + oto 1 đang ở A \( \to {x_{01}} = 0 \to {x_1} = 80t(km)\) + oto 2 đang ở B cách A 200km \( \to {x_{02}} = 200 \to {x_2} = 200 - 80t(km)\) Hai xe gặp nhau khi: \({x_1} = {x_2} \leftrightarrow 80t = 200 - 80t \to t = 1,25h\) Thay vào phương trình của xe 1, ta được vị trí gặp nhau: \(x = {x_1}(t = 1,25h) = 80.1,25 = 100(km)\) => Hai xe gặp nhau sau 1,25h (lúc 8,25h hay 8h15’) chuyển động và tại vị trí cách điểm A 100km, cách B 100km Chọn D Câu hỏi 21 : Trong thí nghiệm về chuyển động thẳng của một vật người ta ghi được vị trí của vật sau những khoảng thời gian 0,02s trên băng giấy được thể hiện trên bảng sau: Chuyển động của vật là chuyển động
Đáp án: B Lời giải chi tiết: Đáp án B Vì trong những khoảng thời gian bằng nhau vật quãng đường vật đi được tăng những khoảng đều đặn khác nhau. Câu hỏi 22 : Đồ thị của 3 vật (I), (II), (III) được thể hiện trên hình vẽ: Phương trình chuyển động của vật (II) có dạng như thế nào?
Đáp án: A Phương pháp giải: Phương pháp: Đồ thị xe (II) có độ lớn tọa độ giảm dần theo thời gian như vậy xe hai đạng chuyển động ngược chiều chuyển động Lời giải chi tiết: Cách giải :
Giả sử phương trình xe (II) :có dạng \({x_2} = {x_{02}} + {v_2}\left( {t - {t_{02}}} \right)\) ta có \(\left\{ \begin{array}{l}{x_{02}} = 5m;{x_2} = 0\\{t_{02}} = 0;{t_2} = 5\\{v_2} = \frac{{{x_2} - {x_{02}}}}{{{t_2} - {t_{02}}}} = \frac{{0 - 5}}{{5 - 0}} = - 1\end{array} \right. = > {x_2} = 5 - t\left( m \right)\) Chọn A Câu hỏi 23 : Đồ thị của 3 vật (I), (II), (III) được thể hiện trên hình vẽ: Phương trình chuyển động của vật (III) có dạng như thế nào?
Đáp án: D Phương pháp giải: Phương pháp: Đồ thị xe (III) có độ lớn tọa độ tăng dần theo thời gian Lời giải chi tiết: Cách giải :
Giả sử phương trình xe (III) :có dạng \({x_3} = {x_{03}} + {v_3}\left( {t - {t_{03}}} \right)\) ta có \(\left\{ \begin{array}{l}{x_{03}} = - 5m;{x_3} = 0\\{t_{00}} = 0;{t_3} = 20\\{v_3} = \frac{{{x_3} - {x_{03}}}}{{{t_3} - {t_{03}}}} = \frac{{0 - \left( { - 10} \right)}}{{20 - 0}} = \frac{1}{2}m/s\end{array} \right. = > {x_2} = - 10 + \frac{1}{2}t\left( m \right)\) Chọn D Câu hỏi 24 : Một chất điểm chuyển động thẳng đều có đồ thị tọa độ thời gian như hình vẽ. Phương trình chuyển động của vật là:
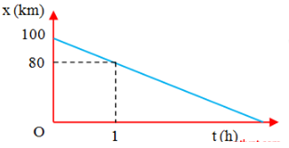
Đáp án: A Phương pháp giải: Phương pháp: Sử dụng phương pháp viết phương trình chuyển động của vật Lời giải chi tiết: Hướng dẫn giải: Phương trình chuyển động: \(x = {x_0} + vt\) Từ đồ thị x-t, ta có: + Tại thời điểm \({t_0} = 0\) : \({x_0} = 100km\) + Tại \(t = 1h\): \(x = 80km = {x_0} + v.1 \to v = \frac{{80 - 100}}{1} = - 20(km/h)\) => phương trình chuyển động của vật: \(x = 100 - 20t(km)\) Chọn A Câu hỏi 25 : Một xe khách chạy với v = 95 km/h phía sau một xe tải đang chạy với v = 75 km/h. Nếu xe khách cách xe tải 110 m thì sau bao lâu nó sẽ bắt kịp xe tải? Khi đó xe tải chạy được một quãng đường bao xa.
Đáp án: D Phương pháp giải: Áp dụng điều kiện hai xe gặp nhau khi \({x_1}\; = {x_2}\;\) Lời giải chi tiết: Chọn gốc toạ độ tại vị trí xe khách chạy Ptcđ có dạng: x1 = 95t ; x2 = 0,11 + 75t Khi hai xe gặp nhau: x1 = x2 Suy ra t = 0,0055 h s2 = v2.t = 0,4125 km Chọn D Câu hỏi 26 : Hai vật xuất phát từ A và B cách nhau 340 m, chuyển động cùng chiều hướng từ A đến B. Vật từ A có v1, vật từ B có v2 = 1/2 v1. Biết rằng sau 136 giây thì 2 vật gặp nhau. Vận tốc vật thứ nhất là:
Đáp án: B Phương pháp giải: Phương pháp : Áp dụng điều kiện hai xe gặp nhau khi \({x_1}\; = {x_2}\;\) Lời giải chi tiết: Cách giải : Chọn gốc toạ độ tại A: x1 = V1t = 136 V1 ; x2 = 340 + 68V1 Khi hai vật gặp nhau: x1 = x2 suy ra V1 = 5 m/s Chọn B Câu hỏi 27 : Lúc 6 giờ sáng, một người đi xe máy khởi hành từ A chuyển động với v = 36 km/h đi về B. Cùng lúc một người đi xe đạp chuyển động với vkđ xuất phát từ B đến A. Khoảng cách AB = 108 km. Hai người gặp nhau lúc 8 giờ. Tìm vận tốc của xe đạp.
Đáp án: C Phương pháp giải: Phương pháp : Áp dụng điều kiện hai xe gặp nhau khi \({x_1}\; = {x_2}\;\) Lời giải chi tiết: Gốc thời gian lúc 2 xe xuất phát, gốc toạ độ tại A. Hai xe xuất phát từ lúc 6 giờ và gặp nhau lúc 8 giờ Suy ra t = 2h Ptcđ có dạng: xm = 36t = 72 xĐ = 108 - 2v2 Khi hai xe đuổi kịp nhau: xm = xĐ suy ra v2 = 18 km/h Chọn C Câu hỏi 28 : Một oto chuyển động thẳng đều từ A đến B với vận tốc 90km/h. Sau 15phút từ B một xe máy chuyển động về A với vận tốc 40km/h. Sau khi đến B oto dừng lại nghỉ 30 phút rồi chuyển động thẳng đều quay trở lại A và gặp xe máy lần 2 ở điểm cách A là 25km (chưa đến A) . Độ dài quãng đường AB là:
Đáp án: B Phương pháp giải: Phương pháp : Áp dụng điều kiện hai xe gặp nhau khi \({x_1}\; = {x_2}\;\) Lời giải chi tiết: Hướng dẫn giải: Ta có: + 15phút = 0,25h, 30 phút = 0,5h Chọn gốc thời gian là lúc xe máy bắt đầu đi, chiều dương từ A đến B, gốc tại A Tọa độ gặp nhau lần thứ 2 của xe máy: \({x_2} = AB - 40t = 25 \to t = \frac{{AB - 25}}{{40}}({\rm{1}})\) Xe máy xuất phát sau oto 15phút, oto nghỉ 30 phút => trong quãng thời gian chuyển động của xe máy oto xuất phát chậm hơn 15phút = 0,25h Tọa độ gặp nhau lần thứ 2 của oto: \({x_1} = 2{\rm{A}}B - 90(t - 0,25) = 25({\rm{2}})\) Từ (1) và (2), ta có:\(2AB - 90(\frac{{AB - 25}}{{40}} - 0,25) = 25 \to AB = 215(km)\) Chọn B Câu hỏi 29 : Hai người đi bộ theo một chiều trên một đường thẳng AB, cùng xuất phát tại vị trí A, với vận tốc lần lượt là 1,5m/s và 2,0m/s, người thứ hai đến B sớm hơn người thứ nhất 5,5min. Quãng đường AB dài
Đáp án: B Phương pháp giải: Thời gian chuyển động \(t = \frac{S}{v}\) Lời giải chi tiết: Đổi 5,5 min = 330 s Thời gian người thứ nhất và người thứ hai đi được lần lượt là: \({t_1} = \frac{S}{{{v_1}}} = \frac{S}{{1,5}};\,\,{t_2} = \frac{S}{{{v_2}}} = \frac{S}{2}\) Người thứ hai đến sớm hơn người thứ nhất 330s, ta có: \({t_1} - {t_2} = 330 \Rightarrow \frac{S}{{1,5}} - \frac{S}{2} = 330 \Rightarrow S = 1980\,\,\left( m \right)\) Chọn B. Câu hỏi 30 : Lúc 7 giờ sáng một xe ô tô xuất phát từ tỉnh A đi đến tỉnh B với vận tốc 60 km/h. Nửa giờ sau một ô tô khác xuất phát từ tỉnh B đi đến tỉnh A với vận tốc 40 km/h. Coi đường đi giữa hai tỉnh A và B là đường thẳng, cách nhau 180 km và các ô tô chuyển động thẳng đều. a. Lập phương trình chuyển động của các xe ôtô. b. Xác định vị trí và thời điểm mà hai xe gặp nhau. Lời giải chi tiết: Chọn trục tọa độ Ox trùng với đường thẳng nối A, B; gốc tọa độ O tại A; chiều dương từ A đến B. Chọn gốc thời gian (t = 0) lúc 7 giờ sáng. Với xe xuất phát từ A: x01 = 0; v1 = 60 km/h; t01 = 0. Với xe xuất phát từ B: x02 = 180 km; v2 = - 40 km/h; t02 = 0,5 h. a) Phương trình tọa độ của hai xe: x1 = x01 + v1(t – t01) = 60t (1) x2 = x02 + v2(t – t02) = 180 – 40(t – 0,5) (2) b) Xác định vị trí và thời điểm mà hai xe gặp nhau. Khi hai xe gặp nhau: x1 = x2 ð 60t = 180 – 40(t – 0,5) delta t = 2 (h); thay t vào (1) hoặc (2) ta có x1 = x2 = 120 km. Vậy hai xe gặp nhau sau 2 giờ kể từ lúc 7 giờ sáng, tức là lúc 9 giờ sáng và vị trí gặp nhau cách A 120 km. Quảng cáo
|