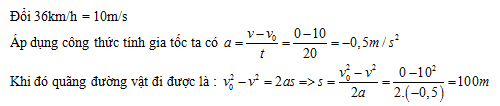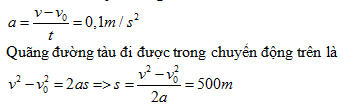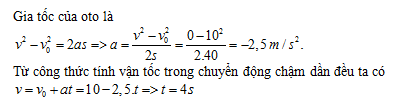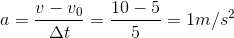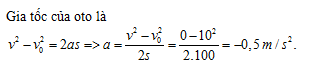30 bài tập Chuyển động thẳng biến đổi đều mức độ vận dụngLàm bàiQuảng cáo
Câu hỏi 1 : Một xe lửa bắt đầu dời khỏi ga và chuyển động thẳng nhanh dần đều với gia tốc 0,1 m/s2. Khoảng thời gian để xe đạt được vận tốc 36km/h là:
Đáp án: D Lời giải chi tiết: Đổi 36km/h = 10 m/s Áp dụng công thức tính vận tốc trong chuyển động nhanh đần đều ta có
Câu hỏi 2 : Một đoàn tàu đang chạy với vận tốc 36km/h thì hãm phanh, chuyển động chậm dần đều và sau 20s thì dừng hẳn. Gia tốc của đoàn tàu là :
Đáp án: A Lời giải chi tiết:
v = 0 Gia tốc của đoàn tàu: Câu hỏi 3 : Chọn câu trả lời đúng. Phương trình chuyển động của vật có dạng: x = 3 - 4t + 2t2 (m;s) Biểu thức vận tốc tức thời của vật theo thời gian là:
Đáp án: C Lời giải chi tiết: Từ phương trình ta có v0 = 4, gia tốc a = 4 Câu hỏi 4 : Một đoàn tàu đang chạy với vận tốc 36km/h thì hãm phanh chuyển động chậm dần đều sau 20s thì dừng hẳn. Quãng đường đoàn tàu đi được kể từ lúc hãm phanh là :
Đáp án: A Lời giải chi tiết: Câu hỏi 5 : Vật chuyển động thẳng biến đổi đều có phương trình: x = 2t2 - 32 , tọa độ tính bằng m, thời gian tính bằng s. Hãy chọn nhận định đúng.
Đáp án: D Lời giải chi tiết: Đáp án D Vật chuyển động thẳng biến đổi đều có phương trình: x = 2t2 - 32 , tọa độ tính bằng m, thời gian tính bằng s. Sau 4s vật có tọa độ bằng 0 Câu hỏi 6 : Vật chuyển động thẳng biến đổi đều có phương trình: x = 5t2 + 3t + 30 , tọa độ tính bằng m, thời gian tính bằng s. Tọa độ ban đầu x0; vận tốc đầu v0; gia tốc a của chuyển động là:
Đáp án: B Lời giải chi tiết: Đáp án B Vật chuyển động thẳng biến đổi đều có phương trình: x = 5t2 + 3t + 30 , tọa độ tính bằng m, thời gian tính bằng s. Tọa độ ban đầu x0; vận tốc đầu v0; gia tốc a của chuyển động là: x0 = 30m; v0 = 3m/s; a = 10m/s2. Câu hỏi 7 : Một đoàn tàu rời ga chuyển động nhanh dần đều. Sau 1 phút 40 giây tàu đạt tốc độ 36km/h. Quãng đường tàu đi được trong 1 phút 40 giây đó là:
Đáp án: A Lời giải chi tiết: Đáp án A Đổi 1 phút 40 giây = 100 giây , 36 km/h = 10 m/s Gia tốc của chuyển động là Câu hỏi 8 : Một xe đạp đang chuyển động thẳng đều với vận tốc 4m/s bỗng hãm phanh và đi chậm dần đều. Mỗi giây vận tốc giảm 0,1m/s. Vận tốc của xe sau khi hãm 10 s là:
Đáp án: A Lời giải chi tiết: Đáp án A Một xe đạp đang chuyển động thẳng đều với vận tốc 4m/s bỗng hãm phanh và đi chậm dần đều. Mỗi giây vận tốc giảm 0,1m/s. Vận tốc của xe sau khi hãm 10 s là: 3m/s Câu hỏi 9 : Một quả cầu được ném thẳng đứng từ mặt đất lên với vận tốc đầu 15m/s. Bỏ qua lực cản không khí. Cho g = 10m/s2. Chọn chiều dương hướng lên. Quả cầu đạt độ cao tối đa là:
Đáp án: B Phương pháp giải: Sử dụng công thức độc lập với thời gian Lời giải chi tiết:
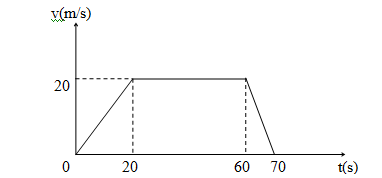
Câu hỏi 10 : Chuyển động của một xe máy được mô tả bởi đồ thị Chuyển động của xe máy là chuyển động
Đáp án: C Lời giải chi tiết: Đáp án C Chuyển động của xe máy là chuyển động đều trong khoảng thời gian từ 20 đến 60s, chậm dần đều trong khoảng thời gian từ 60 đến 70s Câu hỏi 11 : Một viên bi lăn nhanh dần đều từ đỉnh một máng nghiêng với v0 = 0, a = 0,5 m/s2. Sau bao lâu viên bi đạt v = 2,5m/s?
Đáp án: B Phương pháp giải: Áp dụng biểu thức tính gia tốc của chuyển động thẳng biến đổi đều \(a = \dfrac{{v - {v_0}}}{t}\) Lời giải chi tiết: Áp dụng biểu thức tính gia tốc trong chuyển động thẳng đều ta có :\(v = 2,5m/s;a = \dfrac{{v - {v_0}}}{t} = > t = \dfrac{{v - {v_0}}}{a} = \dfrac{{2,5 - 0}}{{0,5}} = 5s\) Chọn B Câu hỏi 12 : Vật chuyển động thẳng có phương trình \(x = 2{t^2} - 4t + 10(m;s)\) . Vật sẽ dừng lại tại vị trí :
Đáp án: D Phương pháp giải: + Vật dừng lại khi có vận tốc bằng 0 - Giải phương trình v = 0 để tìm thời gian t + Thay t vào phương trình chuyển động => vị trí dừng lại Lời giải chi tiết: Phương trình vận tốc của vật: \(v = - 4 + 4t;v = 0 \leftrightarrow - 4 + 4t = 0 \to t = 1{\rm{s}}\) Vật sẽ dừng lại tại vị trí \(x = {2.1^2} - 4.1 + 10 = 8m\) Chọn D Câu hỏi 13 : Một xe máy đang đi với tốc độ 36km/h bỗng người lái xe thấy có một cái hố trước mặt, cách xe 20m người ấy phanh gấp và xe đến sát miệng hố thì dừng lại. Khi đó thời gian hãm phanh là:
Đáp án: C Lời giải chi tiết: Câu hỏi 14 : Một ô tô đang chuyển động thẳng đều với tốc độ 54 km/h thì đợt ngột hãm phanh và dừng lại sau đó 15 s. Coi chuyển động của xe khi hãm phanh là chuyển động chậm dần đều. Quãng đường mà vật đi được trong 2s cuối cùng là
Đáp án: B Phương pháp giải: Áp dụng phương trình chuyển động thẳng chậm dần đều $x={{x}_{0}}+{{v}_{0}}t-\frac{1}{2}a{{t}^{2}}$ Lời giải chi tiết: + Gia tốc chuyển động của xe $a=\frac{0-{{v}_{0}}}{t}=-\frac{15}{15}=-1m/{{s}^{2}}$ . Quãng đường mà vật đi được trong 2 s cuối cùng ${{S}_{2}}={{S}_{15}}-{{S}_{13}}=\left( 15.15-0,{{5.15}^{2}} \right)-\left( 15.13-0,{{5.13}^{2}} \right)=2m$ Đáp án B Câu hỏi 15 : Một ôtô đang chuyển động với vận tốc 5 m/s bổng tăng tốc chuyển động nhanh dần đều sau 5s đạt vận tốc là 10 m/s. Quãng đường mà ô tô đi được kể từ lúc tăng tốc là :
Đáp án: B Lời giải chi tiết: Gia tốc của ô tô là Quãng đường ô tô đi được kể từ lúc tăng tốc: Câu hỏi 16 : Một xe chuyển động nhanh dần đều đi được S = 24m, S2 = 64m trong 2 khoảng thời gian liên tiếp bằng nhau là 4s. Xác định vận tốc ban đầu và gia tốc.
Đáp án: A Phương pháp giải: Áp dụng biểu thức tính vận tốc và quãng đường trong chuyển động thẳng biến đổi đều \(v = {v_0} + at;s = {v_0}t + \frac{1}{2}a{t^2}\) Lời giải chi tiết: Quãng đường vật đi được trong 2 khoảng thời gian liên tiếp bằng nhau là 4s là : \(\begin{array}{l}{S_1}\; = {v_{01}}{t_1} + \frac{1}{2}a{t_1}^24.{v_{01}} + 8a = 24{\rm{ }}\left( 1 \right)\\{S_2} = {v_{02}}{t_2} + \frac{1}{2}a{t_2}^2\;4.{v_{01}} + 8a = 64{\rm{ }}\left( 2 \right)\end{array}\) Mà \({v_{02}} = {v_1} = {v_{01}} + a{t_2}\left( 3 \right)\) Giải (1), (2), (3) ta được : \({v_{01}} = 1m/s,\;a = 2,5m/{s^2}\) Chọn A Câu hỏi 17 : Khi ô tô đang chạy với vận tốc 10 m/s trên đoạn đường thẳng thì người lái xe hãm phanh và ô tô chuyển động chậm dần đều. Cho tới khi dứng hẳn lại thì ô tô đã chạy thêm được 100m. Gia tốc của ô tô là:
Đáp án: A Lời giải chi tiết: Câu hỏi 18 : Một vật chuyển động thẳng nhanh dần đều, trong giây thứ hai vật đi được quãng đường dài 1,5m . Tính quãng đường vật đi được trong giây thứ 100 ?
Đáp án: C Phương pháp giải: Vận dụng phương trình chuyển động của vật Lời giải chi tiết: Gọi a là gia tốc của chuyển động Lại có \({v_0} = 0\) (do vật chuyển động nhanh dần đều) => Phương trình vận tốc của vật là: \(v = at\) + Vận tốc của vật sau giây thứ nhất là \({v_{01}} = a.1 = a\) + Vận tốc của vật sau giây thứ 99: \({v_{099}} = a.99 = 99m/s\) Quãng đường vật đi đư c trong giây thứ 100: \({s_{100}} = {v_{099}}t + \dfrac{1}{2}a{t^2} = 99.1 + \dfrac{1}{2}1.1 = 99,5m\) Chọn C Câu hỏi 19 : Một ô tô đang chuyển động với vận tốc ban đầu là 10 m/s trên đoạn đường thẳng, thì người lái xe hãm phanh,xe chuyển động chậm dần với gia tốc 2m/s2. Quãng đường mà ô tô đi được sau thời gian 3 giây là:
Đáp án: D Phương pháp giải: Công thức tính quãng đường: \(s = {v_0}t + {{a{t^2}} \over 2}\) Lời giải chi tiết: Công thức tính quãng đường: \(s = {v_0}t + {{a{t^2}} \over 2}\) Vật chuyển động chậm dần: \({v_0}\; = 10m/s;{\rm{ }}a = - 2{\rm{ }}m/{s^2}\) Quãng đường ô tô đi được sau thời gian 3s là: \(s = {v_0}t + \frac{{a{t^2}}}{2} = 10.3 + \frac{{( - 2){{.3}^2}}}{2} = 21m\) Chọn D. Câu hỏi 20 : Một chiếc xe đang chuyển động với vận tốc 54 km/h thì người lái xe phát hiện có một vật cản trước mặt, cách vị trí của xe 30 m nên hãm phanh, làm xe chuyển động chậm dần đều. Sau khi hãm phanh 3s, vận tốc của xe còn 10,8 km/h. Tìm gia tốc của xe. Xe có kịp dừng lại trước khi gặp vật cản không?Lời giải chi tiết: Câu hỏi 21 : Một chất điểm bắt đầu chuyển động từ trạng thái nghỉ từ A đến B thì dừng lại, biết chuyển động của vật được chia làm ba giai đoạn. Lúc đầu vật chuyển động thẳng nhanh dần đều trong 10s, sau đó vật chuyển động thẳng đều trong 80s và cuối cùng vật chuyển động thẳng chậm dần đều trong 12s. Biết tổng quãng đường vật đi được là 1820m. Tính quãng đường vật đi được trong mỗi giai đoạn.
Phương pháp giải: Áp dụng công thức quãng đường và vận tốc trong chuyển động thẳng biến đổi đều: \(\left\{ \begin{array}{l} Áp dụng công thức quãng đường và vận tốc trong chuyển động thẳng đều: \(\left\{ \begin{array}{l} Gọi gia tốc trong giai đoạn 1 là a1; quãng đường S1 Cuối giai đoạn 1, ta có vận tốc v1 = a1.t Giai đoạn 2 vật chuyển động với vận tốc là vận tốc cuối của giai đoạn 1: v2 = v1 Giai đoạn 3 vật chuyển động với gia tốc a2 đến khi dừng lại. Lời giải chi tiết: Tóm tắt: v0 = 0. + t1 – t0 = 10 s: vật chuyển động thẳng nhanh dần đều SAC + t2 – t1 = 80 s: vật chuyển động thẳng đều SCD + t3 – t2 = 12 s: vật chuyển động thẳng chậm dần đều SDB SAB = 1820m. Tính SAC; SCD; SDB Giải: Chọn chiều dương là chiều chuyển động - Xét giai đoạn AC: \(\left\{ \begin{array}{l} - Xét giai đoạn CD: \(\left\{ \begin{array}{l} - Xét giai đoạn DB: \(\left\{ \begin{array}{l} Theo bài ra ta có: \({S_1} + {S_2} + {S_3} = 910{a_1} = 1820 \Rightarrow {a_1} = 2\left( {m/{s^2}} \right)\) Nên: \(\left\{ {\begin{array}{*{20}{l}}
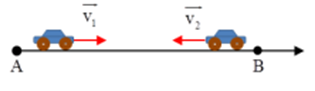
Câu hỏi 22 : Cùng một lúc tại hai điểm A, B cách nhau 125 m có hai vật chuyển động ngược chiều nhau. Vật đi từ A có vận tốc đầu 4 m/s và gia tốc là 2 m/s2, vật đi từ B có vận tốc đầu 6 m/s và gia tốc 4 m/s2. Biết các vật chuyển động nhanh dần đều. Chọn A làm gốc tọa độ, chiều dương hướng từ A đến B, gốc thời gian lúc hai vật cùng xuất phát. Xác định thời điểm hai vật gặp nhau?
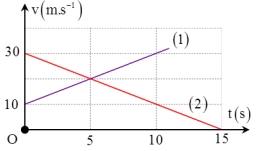
Đáp án: B Phương pháp giải: + Viết phương trình chuyển động của 2 xe + Giải phương trình x1 = x2 + Thay t vào phương trình của 1 xe Lời giải chi tiết: Ta có: + Phương trình chuyển động của hai ô tô lúc này là: \(\left\{ \begin{array}{l}A:{x_1} = 4t + {t^2}\\B:{x_2} = 125 - 6t - 2{t^2}\end{array} \right.\) Chọn B Câu hỏi 23 : Cho đồ thị v - t của hai ôtô như hình vẽ: Chọn phương án đúng?
Đáp án: B Phương pháp giải: Đọc đồ thị v - t Lời giải chi tiết: Từ đồ thị ta suy ra, + Phương trình vận tốc của oto 1 là: \({v_1} = 10 + 2t\) + phương trình vận tốc của oto 2 là: \({v_2} = 30 - 2t\) Chọn B Câu hỏi 24 : Vận tốc của một chất điểm chuyển động dọc theo trục Ox cho bởi hệ thức v = 15 - 8t (m/s). a) Xác định giá trị của gia tốc và vận tốc ban đầu của vật? b) Tính tốc độ của chất điểm lúc t = 2s? Phương pháp giải: a) Công thức vận tốc trong chuyển động thẳng biến đổi đều là v = v0 + at (với a là gia tốc và v0 là vận tốc ban đầu) b) Để xác định tốc độ tại thời điểm t thì ta thay giá trị t = 2s vào phương trình vận tốc Lời giải chi tiết: Tóm tắt: Cho v = 15 - 8t (m/s). a) Tìm v0 và a b) Tìm v tại t = 2s; tốc độ là độ lớn vận tốc |v| Giải: a) Công thức vận tốc trong chuyển động thẳng biến đổi đều là: v = v0 + at (với a là gia tốc và v0 là vận tốc ban đầu) Với \(v = 15 - 8t\left( {m/s} \right) \Rightarrow \left\{ {\begin{array}{*{20}{l}} b) \(t = 2 \Rightarrow v = 15-8.2 = - 1{\rm{ }}m/s \Rightarrow \left| v \right| = 1m/s\) → Tốc độ là 1 m/s. Câu hỏi 25 : Một tàu dời ga chuyển động nhanh dần đều, sau 1 phút tàu đạt 54 km/h. Quãng đường tàu đi được trong giây thứ 60 là: (làm tròn đến chữ số thập phân thứ nhất)
Đáp án: D Phương pháp giải: Áp dụng biểu thức tính quãng đường đi trong giây thứ n là \(\Delta s = {s_n} - {s_{n - 1}}\) Lời giải chi tiết: Gia tốc của vật là \(a = \frac{{v - {v_0}}}{t} = \frac{{15 - 0}}{{60}} = 0,25m/{s^2}\) Quãng đường vật đi được trong 60s đầu là \({s_{60}} = 0.60 + \frac{1}{2}0,{25.60^2} = 450m\) Quãng đường vật đi được trong 59s đầu là \({s_{59}} = 0.59 + \frac{1}{2}0,{25.59^2} = 435,1m\) Quãng đường vật đi được trong giây thứ 60 là \(s = {s_{60}} - {s_{59}} = 450 - 435,1 = 14,9m\) Chọn D Câu hỏi 26 : Lúc 7 h, hai ôtô bắt đầu khởi hành từ hai điểm A, B cách nhau 2400 m, chuyển động nhanh dần đều và ngược chiều nhau. ôtô đi từ A có gia tốc 1 m/s2, còn ôtô từ B có gia tốc 2 m/s2. Chọn chiều dương hướng từ A đến B, gốc thời gian lúc 7h. Xác định thời điểm và vị trí hai xe gặp nhau:
Đáp án: C Phương pháp giải: + Viết phương trình chuyển động của 2 xe + Giải phương trình x1 = x2 + Thay t vào phương trình của 1 xe Lời giải chi tiết: Ta có: + Phương trình chuyển động của hai ô tô lúc này là: \(\left\{ \begin{array}{l}A:{x_1} = \dfrac{1}{2}{t^2}\\B:{x_2} = 2400 - {t^2}\end{array} \right.\) Chọn C Câu hỏi 27 : Một ôtô đang chuyển động với vận tốc 54km/h thì hãm phanh, chuyển động chậm dần đều và dừng lại sau 10s . Chọn chiều dương là chiểu chuyển động của ôtô .Vận tốc của ôtô sau khi hãm phanh được 6s là:
Đáp án: B Phương pháp giải: + Vận dụng biểu thức xác định gia tốc của chuyển động: \(a = \dfrac{{\Delta v}}{{\Delta t}}\) + Viết phương trình vận tốc + Thay t vào phương trình vận tốc Lời giải chi tiết: Đổi \(54km/h = 15m/s\) Gia tốc của xe: \(a = \dfrac{{0 - 15}}{{10}} = - 1,5m/{s^2}\) Phương trình vận tốc của vật: \(v = 15 - 1,5t\) Vận tốc của xe sau khi hãm phanh 6 s là: \(v = 15 - 1,5.6 = 6m/s\) Chọn B Câu hỏi 28 : Một xe ôtô chuyển động chậm dần đều với vận tốc ban đầu v0 = 20m/s và gia tốc 3m/s2. Vận tốc của xe khi đi thêm 50m và quãng đường đi được cho đến khi dừng lại hẳn lần lượt có giá trị là:
Đáp án: B Phương pháp giải: Vận dụng biểu thức độc lập: \({v^2} - v_0^2 = 2{\rm{as}}\) Lời giải chi tiết: Ta có: \({v^2} - v_0^2 = 2{\rm{as}}\) Vận tốc của xe khi đi được quãng đường 50 m: \({v_1}^2 - v_0^2 = 2{\rm{a}}{{\rm{s}}_1} \to v = \sqrt {2{\rm{a}}{{\rm{s}}_1} + v_0^2} = \sqrt {2.( - 3).50 + {{20}^2}} = 10m/s\) Chọn B Câu hỏi 29 : a) Một vật chuyển động thẳng trên trục Ox theo phương trình: x = 4t2 + 20t (cm, s). Xác định vận tốc ban đầu và gia tốc của vật. b) Một người đi xe đạp lên dốc dài 50 m theo chuyển động thẳng chậm dần đều. Vận tốc lúc bắt đầu lên dốc là 5(m/s) và vận tốc cuối dốc là 3 m/s. Tính gia tốc và thời gian lên dốc. Phương pháp giải: pp động học chất điểm Lời giải chi tiết: Một vật chuyển động thẳng trên trục Ox theo phương trình: x = 4t2 + 20t (cm, s). Từ phương trình chuyển độn tổng quát của vật chuyển động thẳng biến đổi đều: \(x = {x_0} + {v_0}.t + \frac{1}{2}.a.{t^2}\) So sánh với đề bài cho ta có vận tốc ban đầu v0 = 20 (cm/s); gia tốc a = 8 (m/s2) b) Áp dụng công thức tính gia tốc độc lập với thời gian ta có: \(\begin{array}{l} Áp dụng công thức tính vận tốc ta có:
Câu hỏi 30 : Hai xe chuyển động ngược chiều nhau trên cùng một đường thẳng từ hai địa điểm A và B cách nhau 400m. Lúc 6 giờ xe thứ nhất qua A với tốc độ v1 = 20m/s, ngay sau đó xe tắt máy chuyển động chậm dần đều với gia tốc 2m/s2 . cùng lúc đó xe thứ 2 qua B chuyển động thẳng đều với tốc độ v2= 72km/h. Chọn trục Ox trùng đường thẳng AB, gốc tọa độ tại A, chiều dương từ A đến B, gốc thời gian là lúc 6 giờ. a, Viết phương trình chuyển động của xe thứ nhất. Xác định quãng đường đi và vận tốc của xe sau 5 giây. b, Viết phương trình chuyển động của xe thứ hai. Xác định vị trí của xe sau 1 phút. c, Tính thời gian chuyển động của xe thứ nhất đến khi dừng. d, Xác định chính xác thời điểm và vị trí 2 xe gặp nhau Phương pháp giải: Động học chất điểm Lời giải chi tiết: Chọn trục Ox trùng đường thẳng AB, gốc tọa độ tại A, chiều dương từ A đến B, gốc thời gian là lúc 6 giờ. Phương trình chuyển động của xe qua thứ nhất (đi từ A sang B ) là: x1 = x0 + v01.t + ½ a.t2 = 20t – t2 (m) (1) phương trình vận tốc là v = 20- 2t (m/s) (2) Vậy sau 5 s thì vận tốc của xe là: v5s = 20 – 2.5 = 10 m/s Quãng đường mà xe thứ nhất đi được sau 5s là: S5s = 20.5 – 52 = 75 m. đổi 72 km/h = 20m/s. Phương trình chuyển động của xe thứ hai là x2 = x02 – v02t = 400 – 20.t (3) Sau 1 phút = 60s thì vị trí của xe 2 là: x2’ = 400 – 20.60 = -800 m. Tức là xe thứ hai đã đi qua A được 800 m. c) Xe thứ nhất khi dừng lại có vận tốc bằng 0. Thay vào phương trình (2) ta có: 0 = 20-2t => t = 10s. d) Sau 10 s thì xe thứ nhất dừng lại, nên vị trí của xe thứ nhất khi đó là: x1 = 20.10 – 102 = 100m. Sau đó dù thời gian trôi đi, xe 1 vẫn đứng yên tại đó, ta chỉ cần xác định thời gian xe 2 đi qua vị trí này. X2 = 400 – 20.t = 100 => t = 15s. Vậy thời điểm hai xe gặp nhau là 6 h + 15 s = 6h 0ph 15s. Vị trí gặp nhau cách A 100m. Quảng cáo
|














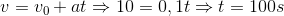
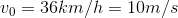
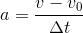 =-10/20 = -0,5 (m/s2)
=-10/20 = -0,5 (m/s2)