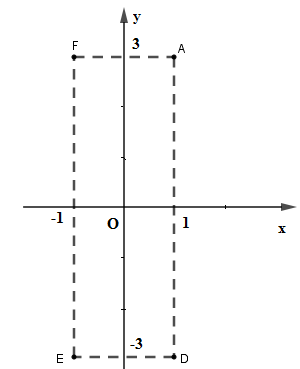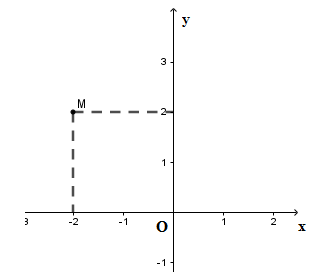25 bài tập tổng hợp về Hàm sốLàm bàiQuảng cáo
Câu hỏi 1 : Khẳng định nào sau đây là đúng:
Đáp án: A Phương pháp giải: - Áp dụng kiến thức về mặt phẳng tọa độ: Điểm nằm trên trục tung có hoành độ bằng 0. Điểm nằm trên trục hoành có tung độ bằng 0. Lời giải chi tiết: Đáp án A đúng, theo kiến thức đã nêu trên. Đáp án B sai vì mọi điểm trên trục hoành có tung độ bằng 0 Đáp án C sai vì mọi điểm trên trục tung có hoành độ bằng 0 Đáp án D sai vì, điểm trên trục hoành có hoành độ từ âm vô cùng đến dương vô cùng. Chọn A. Câu hỏi 2 : Khái niệm hàm số nào sau đây là đúng:
Đáp án: B Phương pháp giải: - Áp dụng kiến thức về mặt phẳng tọa độ: Gốc tọa độ là điểm O có tọa độ (0; 0) Điểm nằm trên trục tung có hoành độ bằng 0 Điểm nằm trên trục hoành có tung độ bằng 0 Lời giải chi tiết: Đáp án A: Sai vì, gốc tọa độ có tọa độ (0; 0) Đáp án B: Đúng, dựa theo kiến thức nêu trên phương pháp Đáp án C: Sai điểm B nằm trên trục hoành không nằm trên trục tung Đáp án D: Sai, vì đơn vị trên 2 trục có thể thay đổi. Chọn B. Câu hỏi 3 : Cho các công thức \(y - 3 = x;\, - 2y = x;\,{y^2} = x\). Có bao nhiêu công thức chứng tỏ rằng \(y\) là hàm số của \(x\)?
Đáp án: C Phương pháp giải: Áp dụng định nghĩa hàm số Lời giải chi tiết: Nhận thấy \(y - 3 = x \Rightarrow y = x + 3\) là một hàm số \( - 2y = x \Rightarrow y = - \frac{x}{2}\) là một hàm số Với \({y^2} = x\) ta thấy khi \(x = 4\) thì \({y^2} = 4\) suy ra \(y = 2\) hoặc \(y = - 2\) nên với một giá trị của \(x\) cho hai giá trị của \(y\) nên \(y\) không là hàm số của \(x.\) Chọn C. Câu hỏi 4 : Nhận định nào sau đây là đúng: Tập hợp các điểm có hoành độ và tung độ bằng nhau là:
Đáp án: A Phương pháp giải: - Áp dụng kiến thức về tọa độ, đường phân giác góc phần tư thứ nhất \(y=x\); đường phân giác góc phần tư thứ hai \(y=-x\) Lời giải chi tiết: Vì điểm đó có tung độ bằng hoành độ, hay chính là \(y=x\). Nên điểm đó nằm trên đường phân giác góc phần tư thứ nhất. Nên đáp án đúng là đáp án A. Chọn A. Câu hỏi 5 : Điểm nào sau đây thuộc hàm số \(y=f(x)=3x\)
Đáp án: B Phương pháp giải: - Áp dụng phương pháp nếu 1 điểm A(x; y ) nằm trên đồ thì hàm số y = f(x), thì tọa độ của điểm A phải thỏa mãn hàm số y = f(x) Lời giải chi tiết: Thay từng kết quả của từng đáp án vào hàm số ta có: \(\begin{align} & A(2;3)\Rightarrow f(x)=3x=3.2=6\ne 3 \\ & B(-1;3-)\Rightarrow f(x)=3x=3.(-1)=-3 \\ & C(4;5)\Rightarrow f(x)=3x=3.4=20\ne 5 \\ & D(1;-3)\Rightarrow f(x)=3x=3.(1)=3\ne -3 \\\end{align}\) Chọn B.
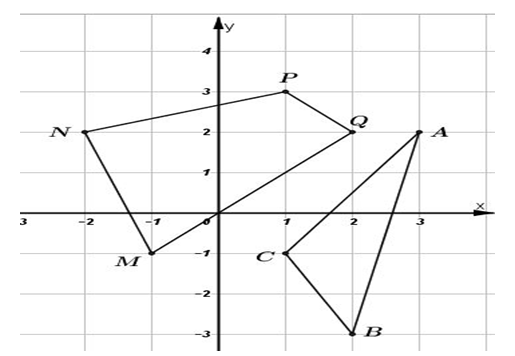
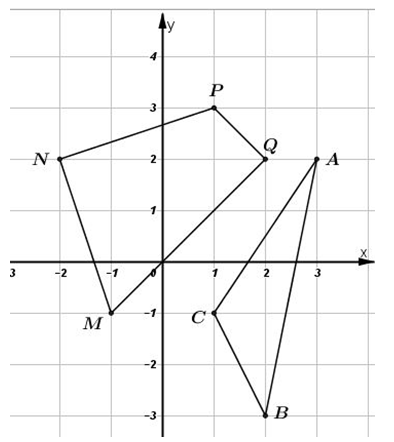
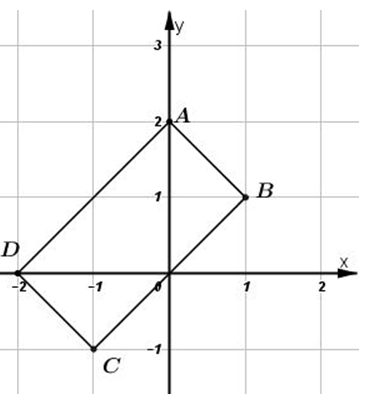
Câu hỏi 6 : Cho hình vẽ sau, hãy tìm tọa độ của các đỉnh tam giác ABC và tứ giác MNPQ Phương pháp giải: - Áp dụng kiến thức về tọa độ để xác định tọa độ của từng điểm trên mặt phẳng. Từ điểm A đường thằng qua A vuông góc với trục hoành cắt trục hoành là hoành độ của điểm A, còn đường thẳng qua A vuông gốc với trục tung cắt trục tung là tung độ của điểm A. Lời giải chi tiết: Dựa vào hình vẽ ta có tọa độ các điểm là: \(\begin{array}{l} Câu hỏi 7 : Vẽ trục tọa độ biểu diễn các điểm sau \(A(0;\,2);B(1;\,\,1);C(-1;\,\,-1);D(-2;\,\,0)\). Tứ giác ABCD là hình gì?
Phương pháp giải: - Xác định tọa độ của từng điểm trên mặt phẳng Oxy bằng cách, x là hoành độ của điểm A, y là tung độ của điểm A, từ hoành độ kẻ đường thưởng vuông góc với trục hoành, từ tung độ kể đường thẳng vuông góc với trụ tung, giao của hai đường đó chính là điểm A có tọa độ (x,y) Lời giải chi tiết: Dựa vào hình vẽ ta thấy hình ABCD là hình chữ nhật. Câu hỏi 8 : Cho hàm số \(y = f\left( x \right) = \frac{{15}}{{2x - 4}}\). Tìm các giá trị của \(x\) sao cho vế phải của công thức có nghĩa.
Đáp án: D Phương pháp giải: Áp dụng \(\frac{A}{B}\) có nghĩa khi \(B \ne 0.\) Lời giải chi tiết: Hàm số \(y = f\left( x \right) = \frac{{15}}{{2x - 4}}\) có nghĩa khi \(2x - 4 \ne 0 \Rightarrow 2x \ne 4 \Rightarrow x \ne 2.\) Chọn D. Câu hỏi 9 : Bảng giá trị nào sau đây là đúng với hàm số \(y = f\left( x \right) = \frac{{15}}{{2x - 3}}\) ?
Đáp án: A Phương pháp giải: Ta thay giá trị đã cho của biến vào công thức và tính giá trị tương ứng của hàm số. Lời giải chi tiết: Tại \(x = - 6\) ta có \(f\left( { - 6} \right) = \frac{{15}}{{2.\left( { - 6} \right) - 3}} = - 1\) Tại \(x = - 3\) thì \(f\left( { - 3} \right) = \frac{{15}}{{2.\left( { - 3} \right) - 3}} = \frac{{ - 15}}{9} = \frac{{ - 5}}{3}\) Tại \(x = - 2\) thì \(f\left( { - 1} \right) = \frac{{15}}{{2.\left( { - 1} \right) - 3}} = \frac{{ - 15}}{5} = - 3\) Tại \(x = 1\) thì \(f\left( 1 \right) = \frac{{15}}{{2.1 - 3}} = - 15\) Nên ta có bảng:
Chọn A. Câu hỏi 10 : Một hàm số được cho bằng công thức \(y = f\left( x \right) = - {x^2} + 2.\) Tình \(f\left( { - \frac{1}{2}} \right);f\left( 0 \right)\)
Đáp án: B Phương pháp giải: Ta thay giá trị đã cho của biến vào công thức và tính giá trị tương ứng của hàm số. Lời giải chi tiết: Ta có \(f\left( { - \frac{1}{2}} \right) = - {\left( { - \frac{1}{2}} \right)^2} + 2 = \frac{{ - 1}}{4} + 2 = \frac{7}{4}\) \(f\left( 0 \right) = - {0^2} + 2 = 2\) Vậy \(f\left( { - \frac{1}{2}} \right) = \frac{7}{4};f\left( 0 \right) = 2.\) Chọn B. Câu hỏi 11 : Một hàm số được cho bằng công thức \(y = f(x) = {x^2}.\) Tính \(f\left( { - 5} \right) + f\left( 5 \right)\)
Đáp án: C Phương pháp giải: Ta thay giá trị đã cho của biến vào công thức và tính giá trị tương ứng của hàm số. Lời giải chi tiết: Ta có \(f\left( { - 5} \right) = {\left( { - 5} \right)^2} = 25\) và \(f\left( 5 \right) = {5^2} = 25\) Nên \(f\left( 5 \right) + f\left( { - 5} \right) = 25 + 25 = 50\) Chọn C. Câu hỏi 12 : Điểm nào dưới đây có tọa độ \(\left( {1; - 3} \right)\)?
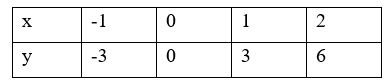
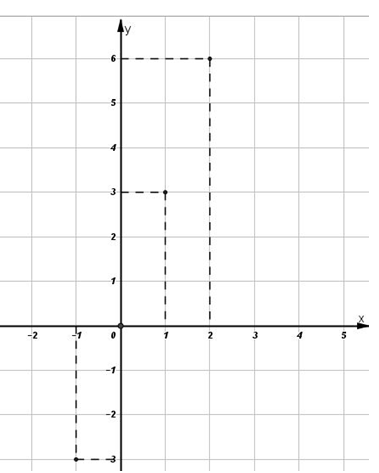
Đáp án: A Phương pháp giải: Xác định tọa độ của các điểm trên hình rồi kết luận Lời giải chi tiết: Từ hình vẽ ta có \(A\left( {1;3} \right);F\left( { - 1;3} \right);D\left( {1; - 3} \right);E\left( { - 1; - 3} \right)\) Nên điểm có tọa độ \(\left( {1; - 3} \right)\) là điểm \(D.\) Chọn A. Câu hỏi 13 : Cho điểm A(x; y); biết rằng \(\frac{x}{y}=\frac{7}{4};x-y=5\). Vậy tọa độ của điểm A là bao nhiêu??
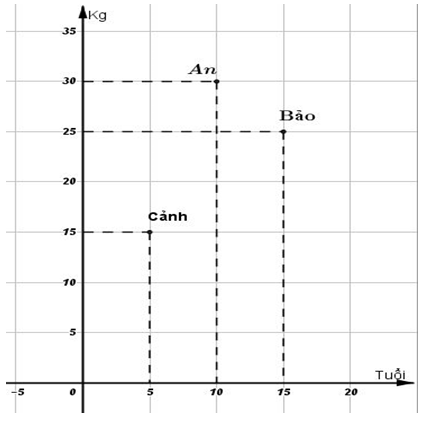
Đáp án: A Phương pháp giải: - Áp dụng kiến thức về tỷ lệ, mà phép toán để tìm được giá trị x và y - Giá trị x, y tìm được chính là tọa độ của điểm A Lời giải chi tiết: Ta có: \(\frac{x}{y}=\frac{7}{4}\Leftrightarrow \frac{x}{7}=\frac{y}{4}.\) Lại có: \(x-y=5.\) Áp dụng tính chất của dãy tỉ số bằng nhau ta có: \(\begin{array}{l} Vậy điểm có tọa độ là: \(\left( \frac{35}{3};\frac{20}{3} \right)\) Chọn A. Câu hỏi 14 : Cho hàm số y như bảng sau: a,Viết tất cả các cặp giá trị tương ứng (x; y) của hàm số trên. b, Hãy biểu diễn hàm số trên trên mặt phẳng tọa độ Oxy. Phương pháp giải: - Từ bảng hàm số x và y, ta sẽ có từng cặp x,y tương ứng. Mỗi cặp x,y là tọa độ của 1 điểm. - Từ các cặp tọa độ trên, chúng ra biểu diễn các điểm đó trên mặt phẳng Oxy Lời giải chi tiết: Có 4 cặp tọa độ (x; y): \(A(-1;-3);\,\,B(0;0);\,\,C(1;\,\,3);\,\,D(2;\,\,6).\) Biểu diễn các điểm A, B, C, D trên mặt phẳng tọa độ như sau: Câu hỏi 15 : Có 3 bạn An, Bảo, Cảnh có số tuổi và cân nặng được biểu diễn trong bảng như sau. Hỏi ai là người có cân nặng cao nhất? Ai là người có tuổi cao nhất, và người đó có cân nặng bao nhiêu?
Phương pháp giải: - Dựa vào mặt phẳng tọa độ, từ điểm An kẻ các đường vuông góc với trục hoành cắt trục hoành tại điểm nào, thì đó là tuổi của An, tương tự từ An kẻ đường thẳng vuông góc với trục tung tại đâu thì đó là cân nặng của An. - Sau khi tìm được cân nặng và tuổi của 3 bạn An, Bảo, Cảnh,(tuổi tương ứng với hoành độ, cân nặng tương ứng với tung độ) - Từ cân nặng và tuổi trả lời các yêu cầu của bài toán. Lời giải chi tiết: Theo đồ thị ta thấy trục hoành biểu diễn tuổi và trục tung biểu diễn cân nặng. Khi đó ta có: An(10; 30); Bảo (15;25); Cảnh (5; 15) Hay bạn An 10 tuổi và nặng 30kg; bạn Bảo 15 tuổi và cân nặng 25kg; bạn Cảnh 5 tuổi và cân nặng 15kg. Như vậy bạn An là người nặng nhất; Bạn Bảo là người có nhiều tuổi nhất và cân nặng 25kg. Câu hỏi 16 : Cho hàm số \(y = f\left( x \right) = 2{x^2} + 3\). Câu 1: Tính \(f\left( 0 \right),f\left( {\frac{1}{2}} \right)\)
Đáp án: D Phương pháp giải: Thay các giá trị của \(x\) vào tính giá trị của hàm số. Lời giải chi tiết: Tính \(f\left( 0 \right),f\left( {\frac{1}{2}} \right)\) Với \(x = 0\) thì \(f\left( 0 \right) = {2.0^2} + 3 = 3\). Với \(x = \frac{1}{2}\) thì \(f\left( {\frac{1}{2}} \right) = 2.{\left( {\frac{1}{2}} \right)^2} + 3 = \frac{7}{2}\). Vậy \(f\left( 0 \right) = 3;f\left( {\frac{1}{2}} \right) = \frac{7}{2}\). Chọn D Câu 2: Tìm \(x\) biết \(f\left( x \right) = 11\).
Đáp án: C Phương pháp giải: Cho \(f\left( x \right) = 11\) và tìm \(x\). Lời giải chi tiết: Tìm \(x\) biết \(f\left( x \right) = 11\). Khi \(f\left( x \right) = 11\) ta có: \(\begin{array}{l}2{x^2} + 3 = 11\\2{x^2} = 11 - 3\\2{x^2} = 8\\{x^2} = 4\\x = \pm 2\end{array}\) Vậy với \(x = \pm 2\) thì \(f\left( x \right) = 11\). Chọn C Câu hỏi 17 : Cho hàm số \(y = 3{x^2} + 1\). So sánh \(f\left( x \right)\) và \(f\left( { - x} \right)\).
Đáp án: C Phương pháp giải: Ta thay giá trị đã cho của biến vào công thức và tính giá trị tương ứng của hàm số. Từ đó so sánh hai kết quả thu được. Lời giải chi tiết: Ta có \(f\left( x \right) = 3{x^2} + 1\) và \(f\left( { - x} \right) = 3{\left( { - x} \right)^2} + 1 = 3{x^2} + 1\) Nên \(f\left( x \right) = f\left( { - x} \right)\) Chọn C. Câu hỏi 18 : Cho hàm số giá trị tuyết đối \(y = f(x) = \left| {3x - 1} \right|\) . Tính \(f\left( { - \frac{1}{4}} \right) - f\left( {\frac{1}{4}} \right)\)
Đáp án: B Phương pháp giải: Ta thay giá trị đã cho của biến vào công thức và tính giá trị tương ứng của hàm số. Lời giải chi tiết: Ta có \(f\left( { - \frac{1}{4}} \right) = \left| {3.\frac{{ - 1}}{4} - 1} \right| = \left| {\frac{{ - 7}}{4}} \right| = \frac{7}{4}\) ; \(f\left( {\frac{1}{4}} \right) = \left| {3.\frac{1}{4} - 1} \right| = \left| { - \frac{1}{4}} \right| = \frac{1}{4}\) . Suy ra \(f\left( { - \frac{1}{4}} \right) - f\left( {\frac{1}{4}} \right) = \frac{7}{4} - \frac{1}{4} = \frac{3}{2}.\) Chọn B. Câu hỏi 19 : Cho hàm số giá trị tuyết đối \(y = f(x) = \left| {3x - 1} \right|\) . Tìm \(x\), biết \(f\left( x \right) = 10.\)
Đáp án: D Phương pháp giải: Phương pháp: Áp dụng \(\left| A \right| = a\) TH1: \(A = a\) TH2: \(A = - a\) Từ đó tìm ra \(x.\) Lời giải chi tiết: Từ \(f\left( x \right) = 10\) ta có \(\left| {3x - 1} \right| = 10\)
Vậy \(x = \frac{{11}}{3}\) hoặc \(x = - 3.\) Chọn D. Câu hỏi 20 : Cho hàm số xác định bởi \(y = f\left( x \right) = 40x + 20\). Với giá trị nào của \(x\) thì \(f\left( x \right) = 300?\)
Đáp án: A Phương pháp giải: Từ đề bài ta đưa về dạng tìm \(x\) quen thuộc. Sử dụng qui tắc chuyển vế để tìm \(x.\) Lời giải chi tiết: Từ \(f\left( x \right) = 300\) ta có \(40x + 20 = 300\) \(40x = 300 - 20 \Rightarrow 40x = 280\) \( \Rightarrow x = 7\) Vậy \(x = 7\) thì \(f\left( x \right) = 300.\) Chọn A. Câu hỏi 21 : Tìm tọa độ điểm \(M\) trên hình vẽ sau:
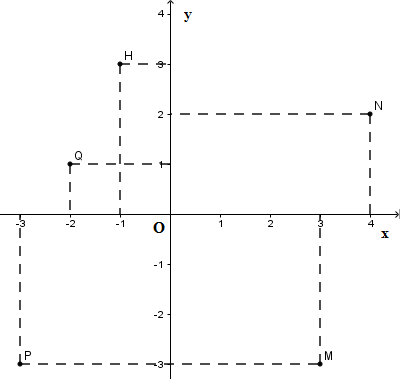
Đáp án: B Phương pháp giải: + Từ điểm đã cho kẻ đường thẳng song song với trục tung, cắt trục hoành tại một điểm biểu diễn hoành độ của điểm đó. + Từ điểm đã cho kẻ đường thẳng song song với trục hoành, cắt trục tung tại một điểm biểu diễn tung độ của điểm đó. + Hoành độ và tung độ tìm được là tọa độ của điểm đã cho Lời giải chi tiết: Tọa độ điểm \(M\) là \(\left( { - 2;2} \right)\) Chọn B. Câu hỏi 22 : Trong các điểm \(M\left( {3; - 3} \right);N\left( {4;2} \right);P\left( { - 3; - 3} \right);Q\left( { - 2;1} \right);H\left( { - 1;3} \right)\) có bao nhiêu điểm thuộc góc phần tư thứ hai?
Đáp án: D Phương pháp giải: Vẽ các điểm trên cùng hệ trục tọa độ rồi kết luận. Lời giải chi tiết: Vẽ các điểm \(M\left( {3; - 3} \right);N\left( {4;2} \right);P\left( { - 3; - 3} \right);Q\left( { - 2;1} \right);H\left( { - 1;3} \right)\) trên cùng mặt phẳng tọa độ.
Ta thấy có hai điểm thuộc góc phần tư thứ hai là \(Q\left( { - 2;1} \right);H\left( { - 1;3} \right).\) Chọn D. Câu hỏi 23 : Trên mặt phẳng tọa độ Oxy, vẽ các điểm \(A\left( { - 2;1} \right),B\left( { - 6;1} \right),C\left( { - 6;6} \right)\) và \(D\left( { - 2;6} \right)\) Tứ giác \(ABCD\) là hình gì?
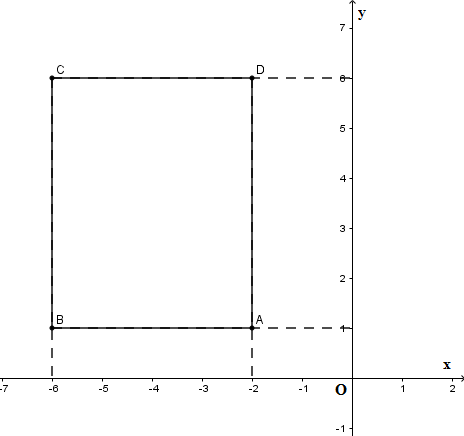
Đáp án: B Phương pháp giải: + Vẽ các điểm \(A\left( { - 2;1} \right),B\left( { - 6;1} \right),C\left( { - 6;6} \right)\) và \(D\left( { - 2;6} \right)\) trên cùng mặt phẳng tọa độ + Từ đó suy ra tính chất của tứ giác\(ABCD\) Lời giải chi tiết:
Vẽ các điểm \(A\left( { - 2;1} \right),B\left( { - 6;1} \right),C\left( { - 6;6} \right)\) và \(D\left( { - 2;6} \right)\) trên cùng mặt phẳng tọa độ. Ta thấy \(ABCD\) là hình chữa nhật. Chọn B. Câu hỏi 24 : Trên mặt phẳng tọa độ Oxy, vẽ các điểm \(A\left( { - 2;1} \right),B\left( { - 6;1} \right),C\left( { - 6;6} \right)\) và \(D\left( { - 2;6} \right)\) Tính diện tích tứ giác \(ABCD.\)
Đáp án: A Phương pháp giải: Sử dụng công thức tính diện tích hình chữ nhật bằng tích chiều dài với chiều rộng. Lời giải chi tiết: Hình chữ nhật \(ABCD\) có \(AB = 4\,cm;\,AD = 5\,cm\) nên diện tích \(ABCD\) bằng \(4.5 = 20\,\left( {c{m^2}} \right).\) Chọn A. Câu hỏi 25 : Cho hàm số \(y=f(x)=|2+x|\), tìm x biết rằng: \(y=f(x)=3\) Phương pháp giải: - Áp dụng kiến thức nếu f(x0) = a, là giá trị của f(x) tại x0 có giá trị là a - Áp dụng kiến thức về tìm x, trong phép toán có dấu trị tuyệt đối. Lời giải chi tiết: Ta có: \(f(x)=\,|2+x|\) \(\Rightarrow f(x)=3\Rightarrow |2+x|=3\) TH1: Với \(x+2\ge 0\Leftrightarrow x\ge -2\) ta có: \(\begin{align} & x+2=3 \\ & x\,\,\,\,\,\,\,\,\,\,\,=3-2 \\ & x\,\,\,\,\,\,\,\,\,\,\,=1\,\,\,\,\left( tm \right). \\ \end{align}\) TH2: Với \(x+2<0\Leftrightarrow x<-2\) ta có: \(\begin{align} & -\left( x+2 \right)=3 \\ & -x-2\,\,\,\,\,\,\,=3 \\ & -x\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,=3+2 \\ & -x\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,=5 \\ & \,\,\,\,x\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,=-5\,\,\,\left( tm \right) \\ \end{align}\) Vậy với \(x\in \text{ }\!\!\{\!\!\text{ -5;1 }\!\!\}\!\!\text{ }\)thì \(y=f(x)=3\). Quảng cáo
|