25 bài tập cơ bản Đồ thị của hàm số y=ax+b (a khác 0)Làm bàiQuảng cáo
Câu hỏi 1 : “ĐTHS \(y=\text{ax}+b(a\ne 0)\) cắt trục hoành tại điểm có hoành độ bằng ….. và cắt trục tung tại điểm có tung độ bằng ……” Trong dấu “…” là gì?
Đáp án: B Phương pháp giải: Phương pháp: - Sử dụng lý thuyết được học: ĐTHS cắt trục hoành, trục tung - So sánh với đề bài để tìm ra biểu thức cần điền vào chỗ trống. Lời giải chi tiết: Cách giải: ĐTHS \(y=\text{ax}+b\) cắt trục hoành \(\Rightarrow y=0\Rightarrow \text{ax}+b=0\Leftrightarrow x=-\frac{b}{a}\) ĐTHS \(y=\text{ax}+b\) cắt trục tung \(\Rightarrow x=0\Rightarrow y=\text{a}\text{.0}+b\Rightarrow y=b\) Chọn B. Câu hỏi 2 : Điểm nào sau đây thuộc ĐTHS \(y=2\text{x}+1\):
Đáp án: A Phương pháp giải: Phương pháp: Sử dụng kiến thức: Điểm \(({{x}_{0}};{{y}_{0}})\) thuộc ĐTHS \(y=\text{ax}+b\Leftrightarrow \text{a}{{\text{x}}_{0}}+b={{y}_{0}}\). Lời giải chi tiết: Cách giải: Ta có \(\text{a}{{\text{x}}_{0}}+b=2.0+1=1={{y}_{0}}\Rightarrow (0;1)\) thuộc ĐTHS đã cho. Chọn A.
Câu hỏi 3 : Với giá trị nào của \(m\) thì điểm \(\left( 1;2 \right)\) thuộc đường thẳng \(x-y=m\)?
Đáp án: D Phương pháp giải: Phương pháp: Điểm \(({{x}_{0}};{{y}_{0}})\)thuộc ĐTHS \(y=\text{ax}+b\Leftrightarrow \text{a}{{\text{x}}_{0}}+b={{y}_{0}}\). Lời giải chi tiết: Cách giải: Điểm \((1;2)\) thuộc ĐTHS \(x-y=m\Leftrightarrow 1-2=m\Leftrightarrow -1=m\). Chọn D.
Câu hỏi 4 : Điểm nào sau đây thuộc đồ thị hàm số \(y = 2x + 1\) ?
Đáp án: D Phương pháp giải: Thay các điểm ở từng đáp án vào hàm số. Lời giải chi tiết: Ta có: \(2.0 + 1 = 1 \Rightarrow N\left( {0;1} \right)\) thuộc đồ thị hàm số \(y = 2x + 1\). Chọn D. Câu hỏi 5 : Hệ số góc của đường thẳng \(\left( d \right):\,\,y = - 2x + 3\) là:
Đáp án: A Phương pháp giải: Đường thẳng \(y = ax + b\) có hệ số góc là \(a.\) Lời giải chi tiết: Ta có: đường thẳng \(y = - 2x + 3\) có hệ số góc là \(a = - 2.\) Chọn A. Câu hỏi 6 : Đồ thị hàm số \(y = 2x - 1\) đi qua điểm
Đáp án: B Phương pháp giải: Thay tọa độ các điểm vào công thức hàm số và chọn đáp án đúng. Lời giải chi tiết: Thay \(x = 2\) vào hàm số \(y = 2x - 1 \Rightarrow 2.2 - 1 = 3 = y\) Vậy \(N\left( {2;\,\,3} \right)\) thuộc đồ thị hàm số. Chọn B. Câu hỏi 7 : Giá trị của \(m\) để đường thẳng \(y=(m-1)x-m\) cắt trục tung tại điểm có tung độ là \(1+\sqrt{2}\) là:
Đáp án: A Phương pháp giải: Phương pháp: Sử dụng kiến thức ĐTHS bậc nhất cắt trục \(Oy\) tại điểm \((0;b)\) và tính toán. Lời giải chi tiết: Cách giải: ĐTHS \(y=(m-1)x-m\) cắt trục tung tại điểm có tung độ là \(1+\sqrt{2}\) \(\Rightarrow -m=1+\sqrt{2}\Rightarrow m=-1-\sqrt{2}\) Chọn A. Câu hỏi 8 : Điểm \(\left( -2;3 \right)\) thuộc đường thẳng nào trong các đường thẳng có phương trình sau:
Đáp án: C Phương pháp giải: Phương pháp: - Điểm \(({{x}_{0}};{{y}_{0}})\) thuộc ĐTHS \(y=\text{ax}+b\Leftrightarrow \text{a}{{\text{x}}_{0}}+b={{y}_{0}}\). - Tính toán và chọn đáp án phù hợp. Lời giải chi tiết: Cách giải: Ta có \(3(-2)-2.3=-12\ne 3\)=> loại A \(3(-2)-3=-9\ne 0\) => loại B \(0(-2)+3=3\) Chọn C. Câu hỏi 9 : ĐTHS \(y=\frac{1}{2}x-3\)và \(y=-x+3\)cắt nhau tại điểm :
Đáp án: D Phương pháp giải: Phương pháp: Sử dụng kiến thức: \(2\) đường thẳng cắt nhau: Xét phương trình hoành độ giao điểm \(2\) đường thẳng rồi tính toán. Lời giải chi tiết: Cách giải: Xét phương trình hoành độ giao điểm: \(\begin{align} & \frac{1}{2}x-3=-x+3\Leftrightarrow \frac{3}{2}x=6\Leftrightarrow x=4 \\ & \Rightarrow y=-4+3=-1. \\\end{align}\) Chọn D. Câu hỏi 10 : ĐTHS \(y=(3-m)x+m+3\) đi qua gốc tọa độ khi:
Đáp án: A Phương pháp giải: Phương pháp: Sử dụng kiến thức: Điểm thuộc đồ thị hàm số. Lời giải chi tiết: Cách giải: Ta có điểm \(O\left( 0~;0 \right)\) thuộc đường thẳng \(y=(3-m)x+m+3\Leftrightarrow m+3=0\Leftrightarrow m=-3\) Chọn A. Câu hỏi 11 :
Tìm giá trị của \(m\) để đồ thị của hàm số \(y = (m - 2017)x + 2018\) đi qua điểm \((1\,;\,\,1)\) ta được
Đáp án: B Phương pháp giải: Thay tọa độ của điểm \((1\,;\,\,1)\) vào hàm số \(y = (m - 2017)x + 2018\) để tìm giá trị của \(m\). Lời giải chi tiết: Đồ thị của hàm số \(y = (m - 2017)x + 2018\) đi qua điểm \((1\,;\,\,1)\) nên ta có: \(1 = (m - 2017).1 + 2018 \Rightarrow 1 = m - 2017 + 2018 \Rightarrow m = 0\) Vậy để đồ thị của hàm số \(y = (m - 2017)x + 2018\) đi qua điểm \((1\,;\,\,1)\) thì \(m = 0\). Chọn B. Câu hỏi 12 : Trong các hàm số dưới đây, hàm số bậc nhất có đồ thị đi qua điểm \(A\left( {1;4} \right)\)là:
Đáp án: C Phương pháp giải: Thay giá trị \(A\left( {1;4} \right)\) vào lần lượt các đáp án Lời giải chi tiết: +) Theo đầu bài hàm số cần tìm là hàm số bậc nhất, nên A.\(y = {x^2} + 3\) là hàm số bậc 2 nên loại +) Lần lượt thay \(x = 1\) vào các hàm số: \(\begin{array}{l} - )\;y = x - 3 = 1 - 3 = - 2\\ - )\;y = 4x = 4.1 = 4\\ - )\;y = 4 - x = 4 - 1 = 3\end{array}\) Như vậy ta thấy điểm \(A\left( {1,4} \right)\) thuộc đồ thị hàm số \(y = 4x\) Chọn đáp án C. Câu hỏi 13 : Tìm \(a;b\) để đồ thị hàm số \(y = ax + b\) thỏa mãn : Câu 1: Đi qua \(M\left( {1;2} \right)\) và song song với đường thẳng \(y = x - 2\).
Đáp án: A Phương pháp giải: Đường thẳng \(y = ax + b\) song song với đường thẳng \(y = a'x + b'\) khi và chỉ khi \(\left\{ \begin{array}{l}a = a'\\b \ne b'\end{array} \right.\) Đường thẳng \(y = ax + b\) đi qua \(M\left( {{x_0};{y_0}} \right)\) khi \({y_0} = a{x_0} + b\) Lời giải chi tiết: Đường thẳng \(y = ax + b\,\,\left( d \right)\) song song với đường thẳng \(y = x - 2 \Rightarrow a = 1 \Rightarrow y = x + b\) \(\left( d \right)\) đi qua \(M\left( {1;2} \right) \Rightarrow 2 = 1 + b \Rightarrow b = 1\) Vậy hàm số cần tìm \(y = x + 1\) Câu 2: Đi qua 2 điểm \(M\left( {1;2} \right)\) và \(N\left( { - 1;0} \right)\)
Đáp án: B Phương pháp giải: Đường thẳng \(y = ax + b\) đi qua \(M\left( {{x_0};{y_0}} \right)\) khi \({y_0} = a{x_0} + b\) Lời giải chi tiết: Đường thẳng \(y = ax + b\) đi qua 2 điểm \(M\left( {1;2} \right)\) và \(N\left( { - 1;0} \right)\) suy ra ta có: \(\left\{ \begin{array}{l}2 = a + b\\0 = - a + b\end{array} \right. \Rightarrow a = b = 1\) Vậy hàm số \(y = x + 1\) Câu hỏi 14 : Nếu đồ thị hàm số \(y = \frac{1}{2}x - b\) cắt trục hoành tại điểm có hoành độ bằng 2 thì giá trị của \(b\) là:
Đáp án: D Phương pháp giải: Thay điểm đi qua vào hàm số. Lời giải chi tiết: Hàm số \(y = \frac{1}{2}x - b\) cắt trục hoành tại điểm có hoành độ bằng 2 \( \Rightarrow \left( {2;0} \right)\) thuộc đồ thị hàm số. Khi đó ta có: \(0 = \frac{1}{2}.2 - b \Leftrightarrow b = 1\). Vậy \(b = 1\). Chọn D. Câu hỏi 15 : Cho đường thẳng \(d:y=x-1\). Khi đó khoảng cách từ gốc tọa độ đến đường thẳng đã cho là:
Đáp án: C Phương pháp giải: Phương pháp: - Tìm giao điểm của đường thẳng với trục hoành, trục tung - Dựng hình chiếu của tam giác được tạo thành - Áp dụng hệ thức trong tam giác để tính khoảng cách từ điểm \(O\) đến \(1\) đường thẳng. - Tính kết quả thu được Lời giải chi tiết: Cách giải: Ta có: \(\begin{align} & d\cap Ox=A(1;0)\Rightarrow OA=1 \\ & d\cap Oy=B(0;-1)\Rightarrow OB=1 \\\end{align}\) Ta có \(OA\bot OB\). Gọi \(H\) là hình chiếu của \(O\) trên đường thẳng \(AB\). Áp dụng hệ thức trong tam giác ta có: \(\begin{align} & \frac{1}{O{{H}^{2}}}=\frac{1}{O{{A}^{2}}}+\frac{1}{O{{B}^{2}}}=\frac{1}{1}+\frac{1}{1}=2 \\ & \Rightarrow OH=\frac{\sqrt{2}}{2} \\\end{align}\) Chọn C.
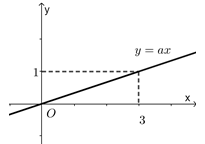
Câu hỏi 16 : Cho hàm số \(y = ax\) có đồ thị như hình bên. Giá trị của \(a\) bằng:
Đáp án: C Phương pháp giải: Thay tọa độ điểm thuộc đồ thị vào hàm số để tìm hệ số \(a\) Lời giải chi tiết: Ta thấy \(M\left( {3;1} \right)\) thuộc đồ thị hàm số nên \(1 = a.3 \Leftrightarrow a = \frac{1}{3}\) Chọn C. Câu hỏi 17 : Trong các hàm số sau, đồ thị hàm số nào là đường thẳng tạo với trục hoành một góc \({45^0}.\)
Đáp án: C Phương pháp giải: Gọi \(\alpha \) là góc tạo bởi đường thẳng \(d:\,\,y = ax + b\,\,\,\left( {a \ne 0} \right)\) với trục hoành. Ta có: \(\tan \alpha = a \Rightarrow \alpha \) là góc nhọn nếu \(a > 0,\,\,\alpha \) là góc tù nếu \(a < 0.\) Lời giải chi tiết: Đường thẳng tạo với trục hoành góc \({45^0} \Rightarrow \tan \alpha = 1.\) Chọn C Câu hỏi 18 : Giá trị của tham số \(m\) để đường thẳng \(y = \left( {2m + 1} \right)x + 3\) đi qua điểm \(A\left( { - 1;\,\,0} \right)\) là:
Đáp án: D Phương pháp giải: Đường thẳng \(d:\,\,y = ax + b\) đi qua điểm \(M\left( {{x_0};\,\,{y_0}} \right) \Leftrightarrow {y_0} = a{x_0} + b.\) Lời giải chi tiết: Đường thẳng \(y = \left( {2m + 1} \right)x + 3\) đi qua điểm \(A\left( { - 1;\,\,0} \right)\) \( \Leftrightarrow 0 = \left( {2m + 1} \right).\left( { - 1} \right) + 3 \Leftrightarrow 2m + 1 = 3 \Leftrightarrow m = 1.\) Chọn D. Câu hỏi 19 : Cho điểm \(M\left( {{x_M};\,\,{y_M}} \right)\) thuộc đồ thị hàm số \(y = - 3{x^2}.\) Biết \({x_M} = - 2.\) Tính \({y_M}.\)
Đáp án: C Phương pháp giải: Điểm \(M\left( {{x_0};\,\,{y_0}} \right)\) thuộc đồ thị hàm số \(y = a{x^2}\,\,\,\left( {a \ne 0} \right) \Rightarrow {y_0} = ax_0^2.\) Lời giải chi tiết: Điểm \(M\left( {{x_M};\,\,{y_M}} \right)\) có hoành độ \({x_M} = - 2\) và thuộc đồ thị hàm số \(y = - 3{x^2}\) \( \Rightarrow {y_M} = - 3.{\left( { - 2} \right)^2} = - 12.\) Chọn C. Câu hỏi 20 : Điểm nào dưới đây thuộc đường thẳng \(y = 3x - 5?\)
Đáp án: B Phương pháp giải: Đường thẳng \(d:\,\,y = ax + b\) đi qua điểm \(M\left( {{x_0};\,\,{y_0}} \right) \Leftrightarrow {y_0} = a{x_0} + b.\) Lời giải chi tiết: +) Xét điểm \(M\left( {3; - 5} \right)\) ta có: \(3.3 - 5 = 4 \ne - 5 \Rightarrow M \notin d:\,\,y = 3x - 5.\) +) Xét điểm \(N\left( {1; - 2} \right)\) ta có: \(3.1 - 5 = - 2 \Rightarrow N \in d:\,\,y = 3x - 5.\) Chọn B. Câu hỏi 21 : Cho hàm số \(f\left( x \right) = 2x + 5;\,\,g\left( x \right) = 2{x^2} - 1\) Câu 1: So sánh \({f^2}\left( 3 \right)\) và \(g\left( 2 \right)\)
Đáp án: D Phương pháp giải: Để tính \(f\left( {{x_0}} \right)\) thay \(x = {x_0}\)vào biểu thức \(f\left( x \right)\) Lời giải chi tiết: Ta có \(f\left( x \right) = 2x + 5 \Rightarrow f(3) = 3.2 + 5 = 11 \Rightarrow {f^2}(3) = 121\) \(g\left( x \right) = 2{x^2} - 1 \Rightarrow g\left( 2 \right) = {2.2^2} - 1 = 7 \Rightarrow {f^2}(3) > g\left( 2 \right)\) Câu 2: Tìm \(x\) để \(g\left( x \right) = f\left( x \right)\).
Đáp án: A Phương pháp giải: Giải phương trình \(f\left( x \right) = g\left( x \right)\) Lời giải chi tiết: \(g\left( x \right) = f\left( x \right) \Leftrightarrow 2x + 5 = 2{x^2} - 1 \Leftrightarrow 2{x^2} - 2x - 6 = 0 \Leftrightarrow x = \dfrac{{1 \pm \sqrt {13} }}{2}\) Vậy \(x = \dfrac{{1 \pm \sqrt {13} }}{2}\) Câu hỏi 22 :
Phương pháp giải: Lời giải chi tiết:
Câu hỏi 23 :
Phương pháp giải: Lời giải chi tiết:
Câu hỏi 24 : Đường thẳng \(y=\text{ax}+b\) đi qua điểm \(\left( 3;2 \right)\). Khi đó \(6a+2b\) bằng:
Đáp án: B Phương pháp giải: Phương pháp: - Sử dụng kiến thức: điểm thuộc đường thẳng. - Biến đổi biểu thức cần tính thành biểu thức có thể tính được theo biểu thức đã xuất hiện - Tính kết quả thu được Lời giải chi tiết: Cách giải: Điểm \(\left( 3;2 \right)\) thuộc đường thẳng \(y=\text{a}x+b\Rightarrow 3a+b=2\) Ta có \(6a+2b=2(3a+b)=2.2=4\) Chọn B. Câu hỏi 25 : Cho \(2\) đường thằng \(d:y=2x-1;d':y=x-3\). Đường thẳng nào đi qua giao điểm của \(d\) và \(d'\)?
Đáp án: A Phương pháp giải: Phương pháp: Sử dụng kiến thức: - Xác định giao điểm của \(2\) đường thẳng - Sử dụng kiến thức điểm thuộc đường thẳng để tìm ra đáp án phù hợp. Lời giải chi tiết: Cách giải: Ta có: \(2x-1=x-3\Leftrightarrow x=-2\Rightarrow y=-5\Rightarrow M(-2;-5)\) Trước hết xét \(M\) có thuộc đường thẳng \(y=3x+1\) không? Ta có \(3.{{x}_{M}}+1=3.(-2)+1=-5={{y}_{M}}\) Chọn A. Quảng cáo
|