Phương pháp giải:

Dựa vào định nghĩa đồ thị hàm số \(y=ax\,\,\left( a\ne 0 \right)\).

Lời giải chi tiết:

Theo định nghĩa  đồ thị hàm số y = ax là một đường thẳng đi qua gốc tọa độ.

Chọn C.

Phương pháp giải:

Thay tọa độ các điểm M, N, P, Q vào hàm số. Điểm nào thỏa mãn hàm số thì điểm đó thuộc hàm số

Lời giải chi tiết:

Thay các điểm M, N, P vào hàm số đều không thỏa mãn, chỉ có điểm Q(-1; 2) thỏa mãn vì: \(2=-2.(-1)\).

Chọn D.

Phương pháp giải:

Xác định điều kiện của x và y của 1 điểm tại góc phần tư thứ (II) trong đồ thị Oxy để chọn điểm phù hợp.

Lời giải chi tiết:

Trong mặt phẳng tọa độ Oxy, tại góc phần tư thứ II tọa độ các điểm có \(x<0\) và \(y>0\).

Thấy có điểm \(\left( -1;\ 3 \right)\)  thỏa mãn điều kiện.

Phương pháp giải:

Để biết một điểm có thuộc đồ thị hàm số hay không ta thay tọa độ điểm đó vào hàm số của đồ thị.

Lời giải chi tiết:

Thay các điểm đã cho vào hàm số \(y =  - 5x\) ta thấy điểm \(\left( {\frac{1}{5}; - 1} \right)\) thuộc đồ thị hàm số.

Chọn B

Phương pháp giải:

Thay tọa độ điểm M vào các hàm số, M không thỏa mãn hàm số nào thì hàm số đó không đi qua điểm M.

Lời giải chi tiết:

Thay điểm M(1; 5) vào hàm số y = -5x ta thấy \(5\ne 1.(-5)=-5\) nên đồ thị hàm số y = -5x không đi qua M(1;5).

Chọn A.

Phương pháp giải:

Thay điểm A lần lượt vào các hàm số, hàm số nào không thỏa mãn thì điểm A không thuộc đồ thị hàm số đó.

Lời giải chi tiết:

Ta thấy: \(6\ne {{3}^{2}}=9\) nên điểm A(-3; 6) không thuộc đồ thị hàm số \(y={{x}^{2}}\)

Chọn D.

Phương pháp giải:

Thay lần lượt các điểm vào hàm số đã cho, điểm nào thỏa mãn hàm số thì điểm đó thuộc đồ thị của hàm số đó.

Lời giải chi tiết:

Đặt \(y=f(x)=5x\).

Xét A(1; 2) có \(x=1;\,\,\,y=2\). Khi đó \(f(1)=5.1=5\ne 2\), tức \(2\ne f(1)\).

Vậy điểm A không thuộc đồ thị hàm số \(y=5x.\)

Xét điểm B(2; 10) có  x = 2; y = 10. Khi đó \(f(2)=5.2=10\), tức là \(10=f(2)\)

Vậy điểm B thuộc đồ thị hàm số \(y=5x.\)

Tương tự ta có \(f(-2)=-10\ne 10;\,\,f\left( \frac{-1}{5} \right)=-1\) nên C không thuộc đồ thị, điểm D thuộc đồ thị trên.

Phương pháp giải:

Thay giá trị của x vào hàm số y = f(x) đã cho.

Lời giải chi tiết:

y = f(x) = \(1 - 2{{\rm{x}}^2}\)

\(y = f\left( {\frac{{ - 1}}{2}} \right) = 1 - 2{\left( {\frac{{ - 1}}{2}} \right)^2} = 1 - 2.\frac{1}{4} = 1 - \frac{1}{2} = \frac{2}{2} - \frac{1}{2} = \frac{1}{2} = 0,5\)

Chọn D.

Phương pháp giải:

Thay các giá trị \(x = a\) vào công thức hàm số \(y = f\left( x \right)\) ta được giá trị \(f\left( a \right).\)

Lời giải chi tiết:

Ta có: \(f\left( { - 2} \right) =  - 2 - 7 =  - 9.\)

Chọn C

Phương pháp giải:

Thay các giá trị của \(x\) vào hàm số \(y =  - 2x\) để tìm giá trị tương ứng của \(y\), từ đó tìm các điểm thuộc đồ thị hàm số đó.

Lời giải chi tiết:

+) Với \(x =  - 1\) thì \(y =  - 2.( - 1) = 2\). Suy ra điểm \(( - 1; - 2)\) không thuộc đồ thị hàm số \(y =  - 2x\).

+) Với \(x = \frac{1}{2}\) thì \(y =  - 2.\frac{1}{2} =  - 1\). Suy ra điểm \(\left( {\frac{1}{2}; - 4} \right)\) không thuộc đồ thị hàm số \(y =  - 2x\).

+) Với \(x = 0\) thì \(y =  - 2.0 = 0\). Suy ra điểm \((0;2)\) không thuộc đồ thị hàm số \(y =  - 2x\).

+) Với \(x =  - 1\) thì \(y =  - 2.( - 1) = 2\). Suy ra điểm \(( - 1;2)\) thuộc đồ thị hàm số \(y =  - 2x\).

Chọn D.

Phương pháp giải:

Điểm \(A\left( {a;b} \right)\) thuộc đồ thị hàm số \(y = 2x\) khi và chỉ khi tọa độ của điểm A thỏa mãn phương trình hàm số: \(y = 2x\) hay \(a = 2b\)

Lời giải chi tiết:

Trong các điểm đã cho chỉ có \(\left( {\frac{1}{3};\frac{2}{3}} \right)\) thỏa mãn đồ thị hàm số \(y = 2x\) hay \(\frac{2}{3} = 2.\frac{1}{3}\)

\( \Rightarrow \left( {\frac{1}{3};\frac{2}{3}} \right)\) thuộc đồ thị hàm số \(y = 2x\) đã cho.

Chọn D

Phương pháp giải:

Thay tọa dộ từng điểm vào hàm số, nếu thỏa mãn thì điểm đó thuộc đồ thị hàm số và ngược lại.

Lời giải chi tiết:

Ta có: \(\frac{2}{3} = 2.\frac{1}{3}\) . Vậy điểm \(\left( {\frac{1}{3};\frac{2}{3}} \right)\) thuộc đồ thị hàm số \(y = 2x\)

Chọn D

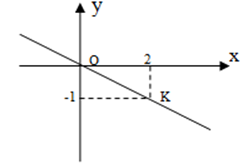
Phương pháp giải:

Thay lần lượt tọa độ các điểm vào hàm số.

Lời giải chi tiết:

Đáp án A : Với \(x = 1\) thì \(y =  - 5.1 =  - 5 \ne 3\) nên điểm \(\left( {1;3} \right)\) không thuộc đồ thị hàm số.

Đáp án B : Với \(x = 1\) thì \(y =  - 5.1 =  - 5\) nên điểm \(\left( {1; - 5} \right)\) thuộc đồ thị hàm số.

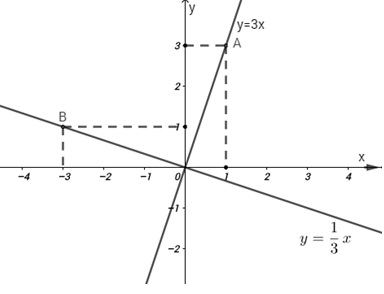
Chọn B.

Phương pháp giải:

Thay K(2; -1) lần lượt vào các hàm số, K thỏa mãn hàm số nào thì OK chính là đồ thị của hàm số đó.

Lời giải chi tiết:

Ta thấy K(2; -1) thỏa mãn hàm số  \(y=-0,5x\) nên OK là đồ thị của hàm số \(y=-0,5x\).

Chọn B.

Phương pháp giải:

Thay lần lượt các điểm vào hàm số \(y=\frac{1}{3}x\), điểm nào thỏa mãn hàm số thì điểm đó là điểm A cần tìm.

Lời giải chi tiết:

Ta thấy A(3; 1) thỏa mãn hàm số \(y=\frac{1}{3}x\).

Chọn C.

Phương pháp giải:

Áp dụng cách vẽ đồ thị hàm số y = ax để vẽ từng đồ thị.

Lời giải chi tiết:

+) Vẽ đồ thị hàm số \(y=3x.\)

Cho \(x=1\) thì \(y=3\) nên \(A\left( 1;\,\,3 \right)\) thuộc đồ thị hàm số \(y=3x.\)

Đường thẳng OA là đồ thị hàm số  \(y=3x.\)

+) Vẽ đồ thị hàm số \(y=\frac{-1}{3}x\) .

Cho \(x=-3\)  thì \(y=1\) nên B(-3; 1) thuộc đồ thị hàm số \(y=\frac{-1}{3}x\).

Đường thẳng OB là đồ thị hàm số \(y=\frac{-1}{3}x\).

Phương pháp giải:

a) Thay tọa đồ điểm M vào hàm số đã cho dể tìm a, từ đó suy ra đồ thị của (C).

b) Thay tọa đồ hai điểm vào hàm số đã cho, điểm nào thỏa mãn hàm số thì điểm đó thuộc đồ thị hàm số.

c) Hai điểm Q, R ta đã biết tung độ hoặc hoành độ, ta thay vào hàm số để tìm ra tọa độ còn lại, từ đó xác định được hai điể Q, R.

Lời giải chi tiết:

a) Đồ thị (C) của hàm số  \(y=ax\,\,\,\left( a\ne 0 \right)\) đi qua M(-3; 5) nên ta có: \(5=a.(-3)\Leftrightarrow a=\frac{-5}{3}\).

Vậy (C) là đồ thị hàm số \(y=\frac{-5}{3}x\).

b) Do \(-5=\frac{-5}{3}.3\) nên \(N(3;\,-5)\in (C)\) .

 Do \(\frac{5}{3}\ne \frac{-5}{3}.1\) nên \(P\left( 1;\,\,\frac{5}{3} \right)\notin \,(C)\) .

c) Điểm \(Q\in (C)\) nên \(2=\frac{-5}{3}x\), suy ra \(x=\frac{-6}{5}\). Vậy \(Q\left( \frac{-6}{5};\,\,2 \right)\).

Điểm \(R\in (C)\)  nên \(y=\frac{-5}{3}.6=-10\). Vậy R(6; -10).

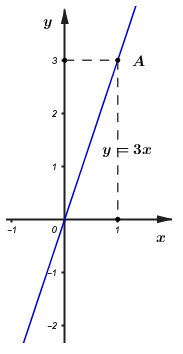
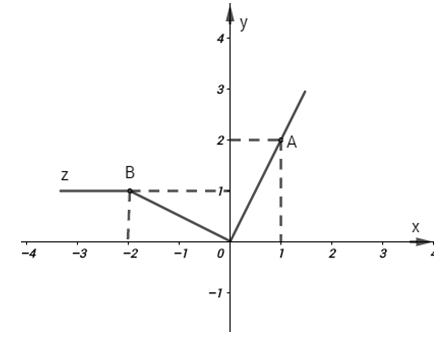
Phương pháp giải:

Muốn chứng minh ba điểm A, B, C thẳng hàng ta chứng minh ba điểm A, B, C cùng thuộc một đồ thị hàm số.

Lời giải chi tiết:

Xét \(A\left( -1;\,\,4 \right)\) ta có: \(4=-4.\left( -1 \right)\) nên điểm A thuộc đồ thị hàm số  \(y=-4x.\)

Xét \(B\left( 2;-8 \right)\)  ta có: \(-8=-4.2\) nên điểm B thuộc đồ thị hàm số \(y=-4x.\)

Xét \(C\left( 1,5;\,\,-6 \right)\) ta có: \(-6=-4.1,5\) nên điểm C thuộc đồ thị hàm số c

Ta thấy ba điểm A, B, C cùng thuộc đồ thị hàm số \(y=-4x\), nên ba điểm A, B, C thẳng hàng.

Phương pháp giải:

a) Đồ thị hàm số \(y = 3x\) đi qua gốc tọa độ \(O\) nên để vẽ đồ thị hàm số đó ta chỉ cần tìm thêm một điểm \(A\) bất kì bằng cách thay \(x\) bởi một giá trị nào đó rồi thay vào hàm số để tìm \(y\) tương ứng.

Đồ thị hàm số \(y = 3x\) chính là đường thẳng đi qua hai điểm \(O\) và \(A\) .

b) Thay \(x =  - 2,\,\, =  - 6\) vào \(y = 3x\), nếu thỏa mãn thì điểm \(M\) đã cho thuộc đồ thị hàm số \(y = 3x\).

Lời giải chi tiết:

a) Vẽ hệ trục tọa độ \(Oxy\).

Với \(x = 1\) ta được \(y = 3\). Điểm \(A\,\,(1\,;\,\,3)\) thuộc đồ thị hàm số \(y = 3x\).

Vậy đường thẳng \(OA\) là đồ thị của hàm số \(y = 3x\).

b) Xét điểm \(M\,( - 2; - 6)\,\, \Rightarrow x =  - 2;\,\,y =  - 6\) , thay vào \(y = 3x\) ta được \( - 6 = 3.( - 2)\) (thỏa mãn).

Vậy điểm \(M{\kern 1pt} \,( - 2;\, - 6)\) thuộc đồ thị hàm số \(y = 3x\).

Phương pháp giải:

Để vẽ được đồ thị hàm số đã cho, ta vẽ từng nhánh một của đồ thị thỏa mãn điều kiện cho trước.

Lời giải chi tiết:

+) Với \(x\ge 0\) ta vẽ đồ thị  hàm số \(y=2x\) đi qua \(O\left( 0;0 \right);\,\,\,A\left( 1;\,\,2 \right).\)

+) Với \(-2<x<0\) ta vẽ đồ thị  hàm số \(y=-\frac{1}{2}x\) là đoạn thẳng đi qua \(O\left( 0;\,\,0 \right);\,\,B\left( -2;\,\,1 \right)\)

+) Với \(x\le -2\) ta vẽ đồ thị hàm số \(y=1\) song song với trục Ox và đi qua \(B\left( -2;\,\,1 \right).\)