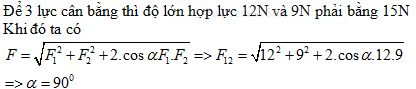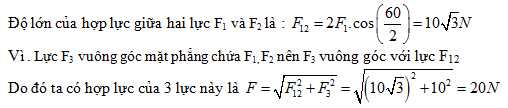20 bài tập Tổng hợp và phân tích lực - điều kiện cân bằng của chất điểm mức độ vận dụngLàm bàiQuảng cáo
Câu hỏi 1 : Cho hai lực đồng qui có cùng độ lớn 600N.Hỏi góc giữa 2 lực bằng bao nhiêu thì hợp lực cũng có độ lớn bằng 600N.
Đáp án: D Lời giải chi tiết: Câu hỏi 2 : Cho hai lực đồng qui có độ lớn F1 = F2 = 30N. Góc tạo bởi hai lực là 120o. Độ lớn của hợp lực :
Đáp án: C Lời giải chi tiết: Câu hỏi 3 : Cho hai lực đồng quy có độ lớn F1 = F2 = 45N. Góc tạo bởi hai lực là 1200. Độ lớn của hợp lực là bao nhiêu?
Đáp án: B Phương pháp giải: Độ lớn của hợp lực: \(F = \sqrt {F_1^2 + F_2^2 + 2{F_1}{F_2}.\cos \alpha } \) Lời giải chi tiết: Ta có: \(\left\{ \begin{array}{l}\overrightarrow F = \overrightarrow {{F_1}} + \overrightarrow {{F_2}} \\\alpha = \left( {\overrightarrow {{F_1}} ;\overrightarrow {{F_2}} } \right) = {120^0}\\{F_1} = {F_2} = 30N\end{array} \right. \Rightarrow F = \sqrt {F_1^2 + F_2^2 + 2{F_1}{F_2}\cos \alpha } = 45N\) Chọn B Câu hỏi 4 : Hợp lực F của hai lực F1 và lực F2 có độ lớn \(8\sqrt 2 N\); lực F tạo với hướng của lực F1 góc 45° và F1 = 8 N. Xác định hướng và độ lớn của lực F2.
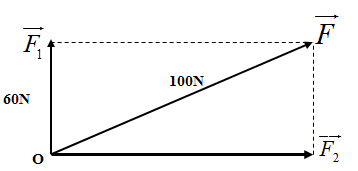
Đáp án: A Phương pháp giải: Phương pháp: Sử dụng các công thức hình học Lời giải chi tiết: Cách giải: Ta có: \(\left\{ \begin{array}{l}F = 8\sqrt 2 N\\{F_1} = 8N\\\left( {\overrightarrow F ;\overrightarrow {{F_1}} } \right) = {45^0}\end{array} \right. \Rightarrow {F_1}\; = F.cos{45^0} \Rightarrow \overrightarrow {{F_2}} \bot \overrightarrow {{F_1}} \) → Độ lớn của F2 là: \({F_2}\; = F.sin{45^0} = 8\sqrt 2 .\sin {45^0} = 8N\) Chọn A Câu hỏi 5 : Phân tích lực \(\overrightarrow F \) thành hai lực \(\overrightarrow {{F_1}} \) và \(\overrightarrow {{F_2}} \), hai lực này vuông góc nhau. Biết F = 100N; F1 = 60N thì độ lớn của lực F2 là:
Đáp án: C Phương pháp giải: - Phân tích lực là thay thế một lực bằng hai hay nhiều lực có tác dụng giống hệt như lực đó. - Phân tích một lực thành hai lực thành phần đồng quy phải tuân theo quy tắc hình bình hành. - Quy tắc hình bình hành: Nếu hai lực đồng quy làm thành hai cạnh của một hình bình hành, thì đường chéo kẻ từ điểm đồng quy biểu diễn hợp lực của chúng. Ta có: \(\overrightarrow F = \overrightarrow {{F_1}} + \overrightarrow {{F_2}} \) Lời giải chi tiết: Theo quy tắc hình bình hành ta có: Vì hai lực \(\overrightarrow {{F_1}} \) và \(\overrightarrow {{F_2}} \) vuông góc với nhau nên áp dụng định lí Pi - ta - go ta có: \({F^2} = F_1^2 + F_2^2 \Rightarrow {F_2} = \sqrt {{F^2} - F_1^2} = \sqrt {{{100}^2} - {{60}^2}} = 80N\) Câu hỏi 6 : Một chất điểm đứng yên dưới tác dụng của 3 lực 12N, 20N, 16N. Nếu bỏ lực 20N thì hợp lực của 2 lực còn lại có độ lớn bằng bao nhiêu ?
Đáp án: B Phương pháp giải: Lời giải chi tiết: Đáp án B Câu hỏi 7 : Cho hai lực đồng quy có độ lớn F1 = F2 = 20 N. Độ lớn của hợp lực là F = 34,6 N khi hai lực thành phần hợp với nhau một góc là
Đáp án: A Phương pháp giải: Độ lớn lực tổng hợp \(F=\sqrt{F_{1}^{2}+F_{2}^{2}+2{{F}_{1}}{{F}_{2}}\text{cos}\alpha }\) Lời giải chi tiết: Độ lớn lực tổng hợp \(F=\sqrt{F_{1}^{2}+F_{2}^{2}+2{{F}_{1}}{{F}_{2}}\text{cos}\alpha }\) Thay số ta được: \(34,6=\sqrt{{{20}^{2}}+{{20}^{2}}+2.20.20\text{cos}\alpha }\Rightarrow \alpha ={{60}^{0}}\) Chọn A Câu hỏi 8 : Lực 10 N là hợp lực của cặp lực nào dưới đây ? Cho biết góc giữa cặp lực đó.
Đáp án: C Phương pháp giải: Phương pháp: Độ lớn của hợp lực: \(F = \sqrt {F_1^2 + F_2^2 + 2{F_1}{F_2}.\cos \alpha } \) Lời giải chi tiết: Cách giải : Áp dụng công thức tính hợp lực: \({F^2} = {F_1}^2 + {F_2}^2 + 2.{F_1}.{F_2}.cos\alpha \) Thử các đáp án ta thấy đáp án C. 3N, 13N; 1800 phù hợp với hợp lực có độ lớn 10N Chọn C Câu hỏi 9 : Một vật chịu 4 lực tác dụng. Lực F1 = 40N hướng về phía Đông, lực F2 = 50N hướng về phía Bắc, lực F3 = 70 N hướng về phía Tây, lực F4 = 90N hướng về phía Nam. Độ lớn của hợp lực tác dụng lên vật là bao nhiêu ?
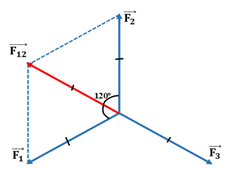
Đáp án: A Phương pháp giải: Phương pháp : Lực tổng hợp : \(\overrightarrow F = \overrightarrow {{F_1}} + \overrightarrow {{F_2}} + \overrightarrow {{F_3}} + \overrightarrow {{F_4}} \) Công thức tính độ lớn của hợp lực : \(F = \sqrt {F_1^2 + F_2^2 + 2{F_1}{F_2}.\cos \alpha } \) Lời giải chi tiết: Cách giải : Ta có : \(\overrightarrow F = \overrightarrow {{F_1}} + \overrightarrow {{F_2}} + \overrightarrow {{F_3}} + \overrightarrow {{F_4}} = \left( {\overrightarrow {{F_1}} + \overrightarrow {{F_3}} } \right) + \left( {\overrightarrow {{F_2}} + \overrightarrow {{F_4}} } \right) = \overrightarrow {{F_{13}}} + \overrightarrow {{F_{24}}} \) Có : \(\left\{ {\begin{array}{*{20}{l}}{{F_{13}}\; = 70--40 = 30{\rm{ }}N}\\{\;{F_{24}}\; = 90--50 = 40{\rm{ }}N}\end{array}} \right.\) Do : \(\overrightarrow {{F_{13}}} \bot \overrightarrow {{F_{24}}} \Rightarrow F = \sqrt {F_{13}^2 + F_{24}^2} = \sqrt {{{30}^2} + {{40}^2}} = 50N\) Chọn A Câu hỏi 10 : Tìm hợp lực của bốn lực đồng quy trong hình vẽ. Biết F1 = 5N, F2 = 3N, F3 = 7N, F4 = 1N
Đáp án: A Phương pháp giải: Phương pháp: Sử dụng quy tắc hình bình hành: Nếu hai lực đồng quy làm thành hai cạnh của một hình bình hành, thì đường chéo kẻ từ điểm đồng quy biểu diễn hợp lực của chúng. Biểu thức: \(\overrightarrow F = \overrightarrow {{F_1}} + \overrightarrow {{F_2}} \) Độ lớn của hợp lực: \(F = \sqrt {F_1^2 + F_2^2 + 2{F_1}{F_2}.\cos \alpha } \) Lời giải chi tiết: Cách giải: Hợp lực của bốn lực đồng quy là: \(\overrightarrow F = \overrightarrow {{F_1}} + \overrightarrow {{F_2}} + \overrightarrow {{F_3}} + \overrightarrow {{F_4}} = \overrightarrow {{F_{13}}} + \overrightarrow {{F_{24}}} \)
Vì \(\left\{ \begin{array}{l}\overrightarrow {{F_1}} \; \nearrow \swarrow \;\overrightarrow {{F_3}} \;\\\overrightarrow {{F_2}} \nearrow \swarrow \;\overrightarrow {{F_4}} \end{array} \right. \Rightarrow \left\{ \begin{array}{l}{F_{13}} = {F_3}--{F_1}\; = 7 - 5 = 2N\\{F_{24}} = {F_2}--{F_4}\; = 3 - 1 = 2N\end{array} \right.\) Vì: \(\overrightarrow {{F_{13}}} \bot \;\overrightarrow {{F_{24}}} \Rightarrow F = \sqrt {F_{13}^2 + F_{24}^2} = \sqrt {{2^2} + {2^2}} = 2\sqrt 2 N\) Chọn A Câu hỏi 11 : Một vật có khối lượng 1 kg được giữ yên trên một mặt phẳng nghiêng bởi một sợi dây song song với đường dốc chính. Biết α = 300. Cho g = 10 m/s2. Lực ép của vật lên mặt phẳng nghiêng là bao nhiêu?
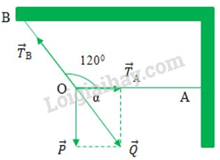
Đáp án: A Phương pháp giải: - Phân tích các lực tác dụng vào vật - Điều kiện cân bằng của một chất điểm là hợp lực của các lực tác dụng lên nó phải bằng không: \(\overrightarrow F = \overrightarrow {{F_1}} + \overrightarrow {{F_2}} + ... = \overrightarrow 0 \) Lời giải chi tiết: Chất điểm chịu tác dụng của các lực: + Trọng lực \(\overrightarrow P \) có độ lớn P = mg = 1.10 = 10N + Lực căng dây \(\overrightarrow T \) + Phản lực \(\overrightarrow Q \) Biểu diễn các lực tác dụng vào vật trên hình vẽ: Phân tích \(\overrightarrow P = \overrightarrow {{P_1}} + \overrightarrow {{P_2}} \) với: \(\overrightarrow {{P_1}} \) song song với mặt phẳng nghiêng; \(\overrightarrow {{P_2}} \) vuông góc với mặt phẳng nghiêng. Điều kiện cân bằng của chất điểm: \(\overrightarrow T + \overrightarrow Q + \overrightarrow {{P_1}} + \overrightarrow {{P_2}} = 0\) Xét theo hai phương song song và vuông góc với mặt phẳng nghiêng: \(\left\{ \begin{array}{l}\overrightarrow T + \overrightarrow {{P_1}} = 0\\\overrightarrow Q + \overrightarrow {{P_2}} = 0\end{array} \right. \Rightarrow \left\{ \begin{array}{l}T = {P_1}\\Q = {P_2}\end{array} \right.\) Từ hình vẽ ta có: \(\left\{ \begin{array}{l}{P_1} = P.\sin \alpha \\{P_2} = P.\cos \alpha \end{array} \right. \Rightarrow \left\{ \begin{array}{l}T = {P_1} = P.\sin \alpha = 10.\sin 30 = 5N\\Q = {P_2} = P.\cos \alpha = 9,8.\cos 30 = 5\sqrt 3 N\end{array} \right.\) Mà lực ép \(\overrightarrow N \) có độ lớn bằng \(\overrightarrow Q \Rightarrow N = 5\sqrt 3 N\) Chọn A Câu hỏi 12 : Một vật có khối lượng 2 kg được giữ yên trên một mặt phẳng nghiêng bởi một sợi dây song song với đường dốc chính. Biết α = 300. Cho g = 10 m/s2. Lực căng của dây treo có độ lớn là:
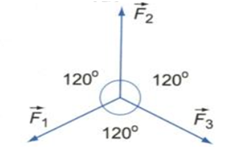
Đáp án: D Phương pháp giải: - Phân tích các lực tác dụng vào vật - Điều kiện cân bằng của một chất điểm là hợp lực của các lực tác dụng lên nó phải bằng không: \(\overrightarrow F = \overrightarrow {{F_1}} + \overrightarrow {{F_2}} + ... = \overrightarrow 0 \) Lời giải chi tiết: Chất điểm chịu tác dụng của các lực: + Trọng lực \(\overrightarrow P \) có độ lớn P = mg = 2.10 = 20N + Lực căng dây \(\overrightarrow T \) + Phản lực \(\overrightarrow Q \) Biểu diễn các lực tác dụng vào vật trên hình vẽ: Phân tích \(\overrightarrow P = \overrightarrow {{P_1}} + \overrightarrow {{P_2}} \) với: \(\overrightarrow {{P_1}} \) song song với mặt phẳng nghiêng; \(\overrightarrow {{P_2}} \) vuông góc với mặt phẳng nghiêng. Điều kiện cân bằng của chất điểm: \(\overrightarrow T + \overrightarrow Q + \overrightarrow {{P_1}} + \overrightarrow {{P_2}} = 0\) Xét theo hai phương song song và vuông góc với mặt phẳng nghiêng: \(\left\{ \begin{array}{l}\overrightarrow T + \overrightarrow {{P_1}} = 0\\\overrightarrow Q + \overrightarrow {{P_2}} = 0\end{array} \right. \Rightarrow \left\{ \begin{array}{l}T = {P_1}\\Q = {P_2}\end{array} \right.\) Từ hình vẽ ta có: \(\left\{ \begin{array}{l}{P_1} = P.\sin \alpha \\{P_2} = P.\cos \alpha \end{array} \right. \Rightarrow \left\{ \begin{array}{l}T = {P_1} = P.\sin \alpha = 20.\sin 30 = 10N\\Q = {P_2} = P.\cos \alpha = 20.\cos 30 = 10\sqrt 3 N\end{array} \right.\) Chọn D Câu hỏi 13 : Một vật có trọng lượng P = 20N được treo vào một vòng nhẫn O (coi là chất điểm). Vòng nhẫn được giữ yên bằng hai dây OA và OB. Biết dây OA nằm ngang và hợp với dây OB một góc là 1200. Tìm lực căng của hai dây OA và OB.
Đáp án: C Phương pháp giải: - Phân tích các lực tác dụng vào vật - Điều kiện cân bằng của một chất điểm là hợp lực của các lực tác dụng lên nó phải bằng không: \(\overrightarrow F = \overrightarrow {{F_1}} + \overrightarrow {{F_2}} + ... = \overrightarrow 0 \) Lời giải chi tiết: Các lực tác dụng vào O gồm: + Lực kéo của vật nặng: \(\overrightarrow P \) (P = 20N) + Lực căng của dây OA: \(\overrightarrow {{T_A}} \) + Lực căng của dây OB: \(\overrightarrow {{T_B}} \) Biểu diễn các lực tác dụng vào vật: Chất điểm O nằm cân bằng: \(\overrightarrow {{T_A}} + \overrightarrow {{T_B}} + \overrightarrow P = 0 \Leftrightarrow \left( {\overrightarrow {{T_A}} + \overrightarrow P } \right) + \overrightarrow {{T_B}} = 0 \Leftrightarrow \overrightarrow Q + \overrightarrow {{T_B}} = 0 \Leftrightarrow \left\{ \begin{array}{l}\overrightarrow Q \uparrow \downarrow \overrightarrow {{T_B}} \\Q = {T_B}\end{array} \right.\) \( \Rightarrow \alpha = \left( {\overrightarrow {{T_A}} ;\overrightarrow Q } \right) = 180 - 120 = {60^0}\) Có \(\overrightarrow {{T_A}} \bot \overrightarrow P \Rightarrow \)Hình bình hành là hình chữ nhật Xét tam giác vuông OTAQ có: \(\left\{ \begin{array}{l}{T_A} = \dfrac{P}{{\tan \alpha }} = \dfrac{{20}}{{\tan 60}} = \dfrac{{20}}{{\sqrt 3 }}N\\Q = \dfrac{P}{{\sin \alpha }} = \dfrac{{20}}{{\sin 60}} = \dfrac{{40}}{{\sqrt 3 }}N\end{array} \right.\) Lại có: \(Q = {T_B} = \dfrac{{40}}{{\sqrt 3 }}N\) Chọn C Câu hỏi 14 : Cho ba lực đồng quy cùng nằm trong một mặt phẳng, có độ lớn bằng nhau và từng đôi một làm thành góc 1200 (hình vẽ). Tìm hợp lực của chúng.
Đáp án: D Phương pháp giải: Sử dụng quy tắc hình bình hành: Nếu hai lực đồng quy làm thành hai cạnh của một hình bình hành, thì đường chéo kẻ từ điểm đồng quy biểu diễn hợp lực của chúng. Biểu thức: \(\overrightarrow F = \overrightarrow {{F_1}} + \overrightarrow {{F_2}} \) Độ lớn của hợp lực: \(F = \sqrt {F_1^2 + F_2^2 + 2{F_1}{F_2}.\cos \alpha } \) Lời giải chi tiết: Ta có: \(\overrightarrow {{F_{123}}} = \overrightarrow {{F_1}} + \overrightarrow {{F_2}} + \overrightarrow {{F_3}} = \overrightarrow {{F_{12}}} + \overrightarrow {{F_3}} \)
Vì \(\left\{ \begin{array}{l}{F_1} = {F_2}\\\left( {\overrightarrow {{F_1}} ;\overrightarrow {{F_2}} } \right) = {120^0}\end{array} \right. \Rightarrow \left\{ \begin{array}{l}{F_{12}} = {F_1} = {F_2}\\\left( {\overrightarrow {{F_{12}}} ;\overrightarrow {{F_2}} } \right) = {60^0}\end{array} \right.\) Do vậy \(\left\{ \begin{array}{l}\overrightarrow {{F_{12}}} \,\, \uparrow \downarrow \,\overrightarrow {{F_3}} \\{F_{12}} = {F_3}\end{array} \right. \Rightarrow \overrightarrow {{F_{123}}} = \overrightarrow {{F_{12}}} + \overrightarrow {{F_3}} = \overrightarrow 0 \) Chọn D Câu hỏi 15 : Cho hai lực đồng quy có cùng độ lớn 10 N. Góc giữa hai lực bằng bao nhiêu thì hợp lực cũng có độ lớn bằng 10 N?
Đáp án: B Phương pháp giải: Phương pháp :
Độ lớn của hợp lực: \(F = \sqrt {F_1^2 + F_2^2 + 2{F_1}{F_2}.\cos \alpha } \) Lời giải chi tiết: Cách giải: Ta có F1 = 10 N; F2 = 10 N; F = 10 N Công thức tính độ lớn của hợp lực : \({F^2} = F_1^2 + F_2^2 + 2{F_1}{F_2}.\cos \alpha \Rightarrow \cos \alpha = \frac{{{F^2} - F_1^2 - F_2^2}}{{2{F_1}{F_2}}} = \frac{{{{10}^2} - {{10}^2} - {{10}^2}}}{{2.10.10}} = - \frac{1}{2} \Rightarrow \alpha = {120^0}\) Chọn B Câu hỏi 16 : Phân tích lực \(\overrightarrow F \) thành lực \(\overrightarrow {{F_1}} \) và vecto lực \(\overrightarrow {{F_2}} \) theo hai phương OA và OB (hình 9 vẽ). Giá trị nào sau đây là độ lớn của hai lực thành phần?
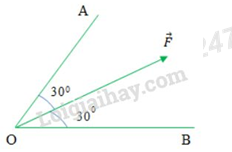
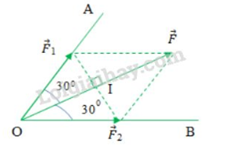
Đáp án: D Phương pháp giải: Phương pháp: Sử dụng quy tắc hình bình hành: Nếu hai lực đồng quy làm thành hai cạnh của một hình bình hành, thì đường chéo kẻ từ điểm đồng quy biểu diễn hợp lực của chúng. Phân tích lực là thay thế một lực bằng hai hay nhiều lực có tác dụng giống hệt như lực đó. Lời giải chi tiết: Cách giải:
Áp dụng quy tắc hình bình hành: Từ điểm ngọn của vecto \(\overrightarrow F \) lần lượt vẽ các đoạn thẳng song song với OA và OB ta đượcr \(\overrightarrow {{F_1}} \) trên OA và \(\overrightarrow {{F_2}} \) trên OB sao cho: \(\overrightarrow F = \overrightarrow {{F_1}} + \overrightarrow {{F_2}} \) Ta có hình bình hành\(O{F_1}F{F_2}\) có đường chéo OF là đường phân giác của góc O nên \(O{F_1}F{F_2}\) là hình thoi Tam giác F1OI vuông tại I có: \(\begin{array}{l}\cos 30 = \frac{{OI}}{{O{F_1}}} \Rightarrow O{F_1} = \frac{{OI}}{{\cos 30}} = \frac{{\frac{{OF}}{2}}}{{\cos 30}} = 0,58.OF\\ \Rightarrow {F_1} = {F_2} = 0,58F\end{array}\) Chọn D Câu hỏi 17 : Một chất chịu hai lực tác dụng có cùng độ lớn 40 N và tạo với nhau góc 1200. Tính độ lớn của hợp lực tác dụng lên chất điểm.
Đáp án: D Phương pháp giải: Phương pháp: Độ lớn của hợp lực: \(F = \sqrt {F_1^2 + F_2^2 + 2{F_1}{F_2}.\cos \alpha } \) Lời giải chi tiết: Cách giải: Độ lớn của hợp lực: \(F = \sqrt {F_1^2 + F_2^2 + 2{F_1}{F_2}.\cos \alpha } = \sqrt {{{40}^2} + {{40}^2} + 2.40.40.\cos 120} = 40N\) Chọn D Câu hỏi 18 : Cho hai lực đồng quy có độ lớn 4(N) và 5(N) hợp với nhau một góc α. Tính góc α ? Biết rằng hợp lực của hai lực trên có độ lớn bằng 7,8(N)
Đáp án: C Phương pháp giải: Phương pháp : Áp dụng quy tắc hình bình hành: \(\overrightarrow F = \overrightarrow {{F_1}} + \overrightarrow {{F_2}} \) Độ lớn của hợp lực: \(F = \sqrt {F_1^2 + F_2^2 + 2{F_1}{F_2}.\cos \alpha } \) Lời giải chi tiết: Cách giải: Ta có F1 = 4 N; F2 = 5 N; F = 7,8 N Công thức tính độ lớn của hợp lực : \({F^2} = F_1^2 + F_2^2 + 2{F_1}{F_2}.\cos \alpha \Rightarrow \cos \alpha = \frac{{{F^2} - F_1^2 - F_2^2}}{{2{F_1}{F_2}}} = \frac{{7,{8^2} - {4^2} - {5^2}}}{{2.4.5}} \Rightarrow \alpha = {60^0}15'\) Chọn C Câu hỏi 19 : Một chất điểm đứng yên dưới tác dụng của 3 lực 12N, 15N, 9N. Hỏi góc giữa 2 lực 12N và 9N bằng bao nhiêu ?
Đáp án: B Lời giải chi tiết: Câu hỏi 20 : Ba lực có cùng độ lớn bằng 10N trong đó F1 và F2 hợp với nhau góc 600. Lực F3 vuông góc mặt phẳng chứa F1, F2. Hợp lực của ba lực này có độ lớn.
Đáp án: D Lời giải chi tiết: Quảng cáo
|














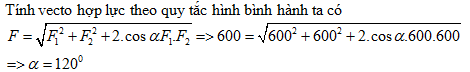
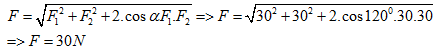
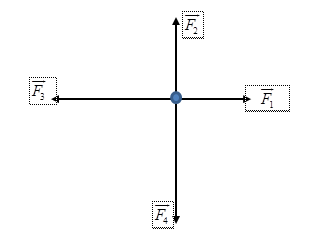
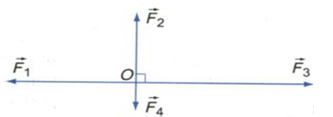
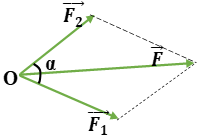
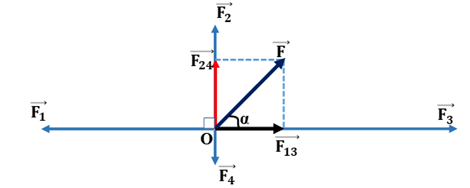
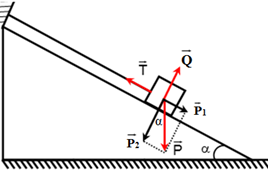
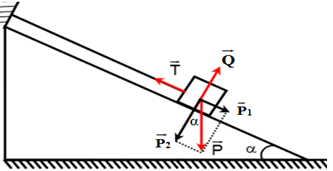
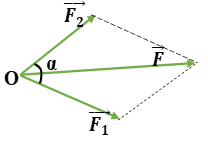
 Áp dụng quy tắc hình bình hành: \(\overrightarrow F = \overrightarrow {{F_1}} + \overrightarrow {{F_2}} \)
Áp dụng quy tắc hình bình hành: \(\overrightarrow F = \overrightarrow {{F_1}} + \overrightarrow {{F_2}} \)