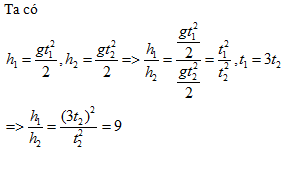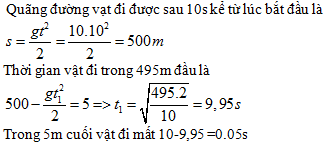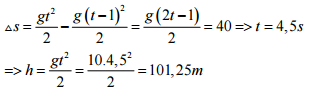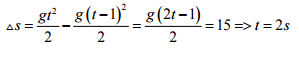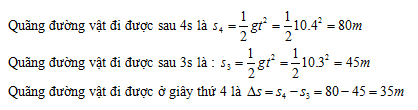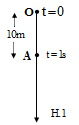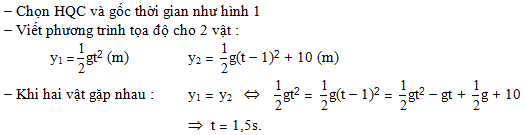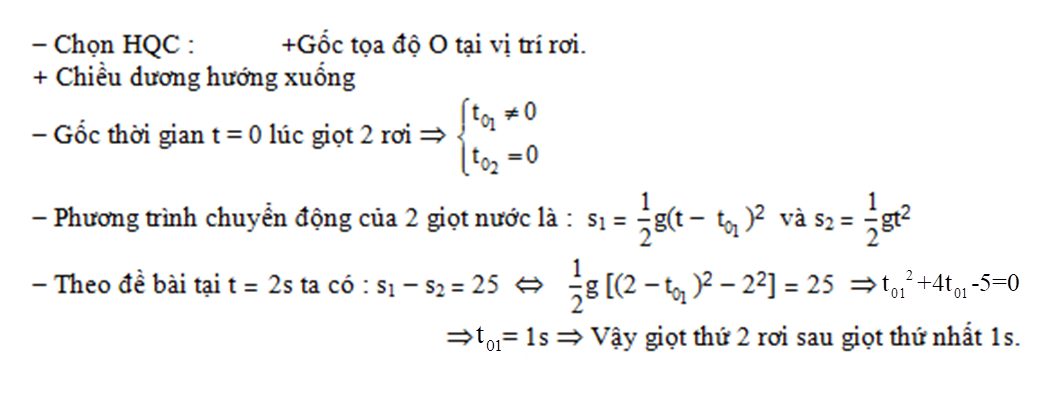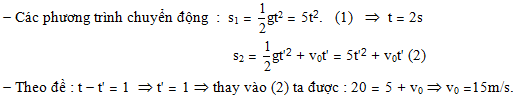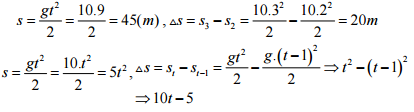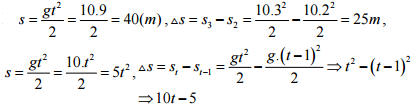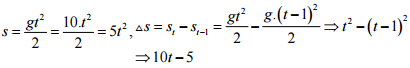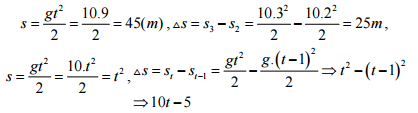20 bài tập Sự rơi tự do mức độ vận dụng

Câu hỏi 1 :

Chọn câu trả lời đúng. Thả vật rơi tự do đồng thời từ hai độ cao h₁≠ h₂. Biết rằng thời gian chạm đất của vật thứ nhất bằng 3 lần của vật thứ hai. Tỉ số h₁ : h₂ là:

A 3
B 9
C 6
D 0,9

Đáp án: B

Phương pháp giải:

Lời giải chi tiết:

Đáp án - Lời giải

Câu hỏi 2 :

Một vật rơi tự do tại nơi g = 10 (m/s²). Thời gian vật rơi là 10 (s). Tính thời gian vật rơi 5 (m) cuối cùng.

A t = 2 (s)
B t = 1 (s)
C t = 0,5 (s)t = 0,5 (s)
D t = 0,05 (s)

Đáp án: D

Phương pháp giải:

Lời giải chi tiết:

Đáp án - Lời giải

Câu hỏi 3 :

Vật rơi tự do trong giây cuối rơi được 40 (m). Tính thời gian vật rơi và độ cao nơi thả vật. Biết g =10 m/s²

A t = 4,5(s), h = 100(m).
B t = 5 (s), h = 100 (m).
C t = 5 (s), h = 120 (m).
D t = 4,5(s), h = 101,25 (m).

Đáp án: D

Phương pháp giải:

Lời giải chi tiết:

Quãng đường trong giây cuối cùng được tính theo công thức

Đáp án - Lời giải

Câu hỏi 4 :

Chọn câu trả lời đúng. Một vật rơi tự do từ một độ cao h. Biết rằng trong giây cuối cùng vật rơi được quãng đường 15 m. Thời gian rơi của vật là:

A 1s
B 1,5s
C 2,5s
D 2s

Đáp án: D

Phương pháp giải:

Lời giải chi tiết:

theo bài ra ta có

Đáp án - Lời giải

Câu hỏi 5 :

Chọn câu trả lời đúng. Hai vật có khối lượng m₁= 3m₂ rơi tự do tại cùng một địa điểm,với v₁, v₂ tương ứng là vận tốc chạm đất của vật thứ nhất và vật thức hai. Bỏ qua sức cản của không khí. Khi đó:

A v₁ > v₂.
B v₁ =2 v₂.
C v₁ = v₂.
D v₂ = 2 v₁.

Đáp án: C

Phương pháp giải:

Lời giải chi tiết:

Đáp án C

Đáp án - Lời giải

Câu hỏi 6 :

Một vật rơi tự do sau 4 giây thì chạm đất. Lấy g = 10 m/s². Quãng đường vật rơi trong giây cuối cùng là

A 75m
B 80m
C 45m
D 35m

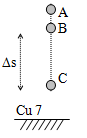
Đáp án: D

Lời giải chi tiết:

Đáp án - Lời giải

Câu hỏi 7 :

Hai viên bi A và B được thả rơi tự do từ cùng độ cao. Bi A rơi sau bi B 0,5s. Tính khoảng cách giữa 2 bi sau 2s.

A 8,75m
B 9,75m
C 10,15m
D 40m

Đáp án: A

Phương pháp giải:

Lời giải chi tiết:

Đáp án - Lời giải

Câu hỏi 8 :

Hai viên bi sắt được thả rơi tự do cùng độ cao cách nhau một khoảng thời gian 0,5s. Lấy g = 10m/s². Khoảng cách giữa hai viên bi khi viên thứ hai rơi được 1,5s là

A 6,25m.
B 20m.
C 8,75m.
D 11,25m.

Đáp án: C

Lời giải chi tiết:

Đáp án C

Đáp án - Lời giải

Câu hỏi 9 :

Người ta ném một vật từ mặt đất lên cao theo phương thẳng đứng với vận tốc 5,0m/s. Lấy g = 10m/s². Thời gian vật chuyển động và độ cao cực đại vật đạt được là (Bỏ qua sức cản của không khí).

A t = 0,5s; h = 1,25m.
B t = 1s; h = 1,25m.
C t = 1s; h = 2,5m.
D t = 0,5s; h = 2,5m.

Đáp án: B

Lời giải chi tiết:

Đáp án B

Đáp án - Lời giải

Câu hỏi 10 :

Một vật rơi tự do không vận tốc đầu từ một điểm M cách mặt đất 50m. Lấy g = 10m/s². Viết phương trình chuyển động của vật khi chọn gốc toạ độ ở mặt đất và chiều dương hướng xuống?

A \(y = 50 + 5{t^2}\,\,\left( m \right)\)
B \(y = - 50 + 5{t^2}\,\,\left( m \right)\)
C \(y = 5{t^2}\,\,\left( m \right)\)
D \(y = - 5{t^2}\,\,\left( m \right)\)

Đáp án: B

Phương pháp giải:

Phương trình chuyển động của vật có dạng tổng quát: \(y = {y_0} + {v_0}\left( {t - {t_0}} \right) + \frac{1}{2}a.{\left( {t - {t_0}} \right)^2}\)

Lời giải chi tiết:

Chọn gốc thời gian là lúc thả rơi vật. Gốc toạ độ ở mặt đất và chiều dương hướng xuống

Phương trình chuyển động của vật có dạng : \(y = {y_0} + {v_0}\left( {t - {t_0}} \right) + \frac{1}{2}a.{\left( {t - {t_0}} \right)^2}\)

Ta có: \(\left\{ \begin{array}{l}{y_0} = {y_M} = - 50m\\{v_0} = 0\\{t_0} = 0\\a = g = 9,8m/{s^2}\end{array} \right. \Rightarrow y = - 50 + \frac{1}{2}.10.{t^2} \Rightarrow y = - 50 + 5{t^2}\,\,\left( m \right)\)

Chọn B

Đáp án - Lời giải

Câu hỏi 11 :

Một vật được thả rơi tự do, khi chạm đất tốc độ của vật là 30 m/s. Chọn gốc tọa độ tại vị trí thả vật, gốc thời gian là lúc thả vật, chiều dương hướng xuống, lấy g = 10m/s². Khi tốc độ của vật là 20 (m/s) thì vật còn cách đất bao nhiêu và sau bao lâu thì vật rơi đến đất (kể từ khi tốc độ của vật là 20m/s).

Phương pháp giải:

Áp dụng công thức:

- Thời gian từ lúc rơi đến khi chạm đất: v = g.t

- Độ cao lúc thả vật:\(h = \frac{{g.{t^2}}}{2}\)

- Công thức độc lập với thời gian:

\(v_{^1}^2 - v_0^2 = 2g{h_1}\)

- Công thức vận tốc v = gt

Lời giải chi tiết:

Tóm tắt:

v_cđ = 30 m/s.

Chọn gốc tọa độ tại vị trí thả vật, gốc thời gian là lúc thả vật, chiều dương hướng xuống, g = 10m/s².

Khi v = 20 (m/s) thì vật còn cách đất bao nhiêu và sau bao lâu thì vật rơi đến đất (kể từ khi tốc độ của vật là 20m/s).

Giải:

+ Thời gian từ lúc rơi đến khi chạm đất:

\(v = g.t \Rightarrow t = 3\,(s)\)

+ Độ cao lúc thả vật:

\(h = \frac{{g.{t^2}}}{2} \Rightarrow h = 45(m)\)

+ Khi tốc độ v₁= 20 m/s, ta có:

\(v_{^1}^2 = 2g{h_1} \Rightarrow {h_1} = 20(m)\)

→ Vật cách mặt đất một đoạn: \(\Delta h = h - {h_1} = 45 - 20 = 25(m)\)

+ Thời gian từ lúc thả đến khi vật đạt tốc độ là 20m/s là t₁:

\({v_1} = g.{t_1} \Rightarrow {t_1} = 2(s) \Rightarrow {t_2} = t - {t_1} = 1(s)\)

Câu hỏi 12 :

Từ một đỉnh tháp người ta buông rơi 1 vật. Một giây sau ở tầng tháp thấp hơn 10m người buông rơi vật thứ 2. Hai vật sẽ gặp nhau sau bao lâu kể từ khi vật thứ nhất được buông rơi. Lấy g = 10m/s².

A t = 0,5s.
B t = 2,5s.
C t = 1,5s.
D t = 3,5s.

Đáp án: C

Phương pháp giải:

Lời giải chi tiết:

Đáp án - Lời giải

Câu hỏi 13 :

Sau 2s kể từ lúc giọt nước thứ 2 bắt đầu rơi, khoảng cách giữa 2 giọt nước là 25m. Tính xem giọt nước thứ 2 được nhỏ rơi trễ hơn giọt nước thứ nhất bao lâu ? Lấy g = 10m/s².

A giọt thứ 2 rơi sau giọt thứ nhất 2s.
B giọt thứ 2 rơi sau giọt thứ nhất 3s.
C giọt thứ 2 rơi sau giọt thứ nhất 4s.
D giọt thứ 2 rơi sau giọt thứ nhất 1s.

Đáp án: D

Phương pháp giải:

Lời giải chi tiết:

Đáp án - Lời giải

Câu hỏi 14 :

Ở một tầng tháp cách mặt đất 45m, một người thả rơi một vật. Một giây sau người đó ném vật thứ 2 xuống theo hướng thẳng đứng. Hai vật chạm đất cùng lúc. Tính vận tốc ném của vật thứ 2. Lấy g = 10m/s².

A v₀ = 12,5cm/s.
B v₀ = 12,5km/s.
C v₀ = 12,5m/s.
D v₀ = 12,5mm/s.

Đáp án: C

Phương pháp giải:

Lời giải chi tiết:

Đáp án - Lời giải

Câu hỏi 15 :

Từ độ cao 20m, phải ném một vật thẳng đứng với vận tốc v₀ bằng bao nhiêu để vật này tới mặt đất sớm hơn 1s so với vật rơi tự do ?

A v₀ =1,5m/s.
B v₀ =150m/s
C v₀ =0,15m/s.
D v₀ =15m/s.

Đáp án: D

Phương pháp giải:

Lời giải chi tiết:

Đáp án - Lời giải

Câu hỏi 16 :

Một giọt nước rơi từ độ cao 10m xuống mặt đất. Nếu không kể đến sức cản không khí thì vận tốc của giọt nước khi chạm đất là :

A 14.14m/s
B 1.4m/s
C 200m/s
D 100m/s

Đáp án: A

Phương pháp giải:

Lời giải chi tiết:

Đáp án - Lời giải

Câu hỏi 17 :

Một vật rơi tự do không vận tốc đầu. Quãng đường rơi trong giây thứ 2 là 14,73m. Suy ra gia tốc trọng lực ở nơi làm thí nghiệm là:

A 9,82 m/s²
B 9,81 m/s²
C 9,80 m/s²
D 7,36 m/s²

Đáp án: A

Phương pháp giải:

Sử dụng công thức tính quãng đường của vật rơi tự do \(s = \frac{{g.{t^2}}}{2}\)

Lời giải chi tiết:

Quãng đường vật rơi trong giây thứ 2 là:

\(s = {s_2} - {s_1} = \frac{{g{{.2}^2}}}{2} - \frac{{g{{.1}^2}}}{2} = \frac{3}{2}g\)

Theo đề bài ta có: \(\frac{3}{2}g = 14,73 \Rightarrow g = 9,82\,\,\left( {m/{s^2}} \right)\)

Chọn A.

Đáp án - Lời giải

Câu hỏi 18 :

Một vật rơi tự do không vận tốc đầu từ một điểm A vào lúc t = 0. Chọn chiều dương hướng xuống, gốc thời gian là lúc vật bắt đầu rơi. Phương trình của vật khi chọn gốc toạ độ là vị trí O ở dưới A một khoảng 196m là :

(Lấy g = 9,8m/s²)

A y = 4,9t² (m)
B y = 4,9t² + 196 (m)
C y = 4,9t² - 196 (m)
D y = 4,9(t - 196)²(m)

Đáp án: C

Phương pháp giải:

Phương trình tổng quát của vật chuyển động thẳng biến đổi đều là:

\(y = {y_0} + {v_0}\left( {t - {t_0}} \right) + {1 \over 2}a{\left( {t - {t_0}} \right)^2}\)

Lời giải chi tiết:

Chọn chiều dương hướng xuống, gốc thời gian là lúc vật bắt đầu rơi. Gốc toạ độ là vị trí O ở dưới A một khoảng 196m.

Phương trình tổng quát của vật chuyển động thẳng biến đổi đều là:

\(y = {y_0} + {v_0}\left( {t - {t_0}} \right) + {1 \over 2}a{\left( {t - {t_0}} \right)^2}\)

Ta có:

\(\left\{ \matrix{
{y_0} = - 196m \hfill \cr
a = g = 9,8m/{s^2} \hfill \cr
{t_0} = 0 \hfill \cr} \right. \Rightarrow y = - 196 + 4,9{t^2}\,\,\left( m \right)\)

Chọn C

Đáp án - Lời giải

Câu hỏi 19 :

Một vật được thả rơi tự do từ độ cao h = 45m so với mặt đất. Bỏ qua lực cản của không khí và lấy g = 10m/s²_.

1.Tính thời gian kể từ vật bắt đầu rơi đến khi chạm đất.

2. Tính quãng đường vật rơi trong 2 giây cuối cùng trước khi chạm đất.

Phương pháp giải:

Áp dụng công thức rơi tự do

Lời giải chi tiết:

Chọn hệ quy chiếu gắn với mặt đất, chiều dương của trục Oy hướng xuống đất, gốc O tại điểm rơi.

a) Ta có thời gian rơi được xác định là

\(t = \sqrt {\frac{{2h}}{g}} = \sqrt {\frac{{2.45}}{{10}}} = 3s\)