20 bài tập Công của lực điện mức độ thông hiểuLàm bàiQuảng cáo
Câu hỏi 1 : Công của điện trường làm dịch chuyển điện tích Q từ điểm A tới điểm B trong điện trường sẽ phụ thuộc vào:
Đáp án: A Phương pháp giải: Lời giải chi tiết: Đáp án A Công của lực điện tác dụng lên một điện tích điểm không phụ thuộc dạng đường đi của điện tích mà chỉ phụ thuộc vào điểm đầu và điểm cuối của đường đi trong điện trường Câu hỏi 2 : Phát biểu nào sau đây về công của lực điện trường là không đúng?
Đáp án: B Phương pháp giải: Công của lực điện trường không phụ thuộc vào hình dạng quỹ đạo mà chỉ phụ thuộc vào vị trí điểm đầu và điểm cuối. Lời giải chi tiết: Công của lực điện trường không phụ thuộc vào hình dạng quỹ đạo mà chỉ phụ thuộc vào vị trí điểm đầu và điểm cuối. Vì vậy nói Công của lực điện trường phụ thuộc vào hình dạng quỹ đạo chuyển động là sai Chọn B Câu hỏi 3 : Công của lực điện trường dịch chuyển một điện tích \(\text{1 }\!\!\mu\!\!\text{ C}\) dọc theo chiều một đường sức trong một điện trường đều 1000 V/m trên quãng đường dài 1 m là
Đáp án: A Phương pháp giải: Áp dụng công thức tính công của lực điện trường: \(\text{A = F}\text{.d = Eqd}\) Lời giải chi tiết: \(\text{A = F}\text{.d = Eqd = 1000}\text{.1}{{\text{0}}^{-6}}.1={{10}^{-3}}(\text{J})=\text{1 mJ}\) Chọn A Câu hỏi 4 : Công của lực điện trường khác 0 trong khi điện tích
Đáp án: A Lời giải chi tiết: Công của lực điện trường khác 0 trong khi điện tích dịch chuyển giữa 2 điểm khác nhau cắt các đường sức. Câu hỏi 5 : Khi điện tích dich chuyển dọc theo một đường sức trong một điện trường đều, nếu quãng đường dịch chuyển tăng 2 lần thì công của lực điện trường
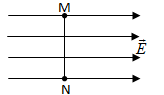
Đáp án: B Lời giải chi tiết: Áp dụng công thức tính công A = qEd. Khi khoảng cánh tăng hai làn thì công tăng lên 2 lần Câu hỏi 6 : Một điện tích điểm q di chuyển từ điểm M đến N trong điện trường đều như hình vẽ. Khẳng định nào sau đây đúng?
Đáp án: C Phương pháp giải: Lời giải chi tiết: Đáp án C Câu hỏi 7 : Dưới tác dụng của lực điện trường, một điện tích q > 0 di chuyển được một đoạn đường s trong điện trường đều theo phương hợp với \(\vec E\) góc a. Trong trường hợp nào sau đây, công của điện trường lớn nhất?
Đáp án: A Phương pháp giải: Lời giải chi tiết: Đáp án A Câu hỏi 8 : Cho điện tích thử q di chuyển trong một điện trường đều dọc theo hai đoạn thẳng MN và NP. Biết rằng lực điện sinh công dương và MN dài hơn NP. Hỏi kết quả nào sau đây là đúng, khi so sánh các công AMN và ANP của lực điện ?
Đáp án: D Phương pháp giải: Phương pháp: - Công thức tính công của lực điện: A = Fscosα = qEd - Công của lực điện trong sự di chuyển của một điện tích không phụ thuộc hình dạng đường đi mà chỉ phụ thuộc vị trí điểm đầu và điểm cuối của đường đi trong điện trường Lời giải chi tiết: Cách giải:
Công của lực điện trong sự di chuyển của một điện tích không phụ thuộc hình dạng đường đi mà chỉ phụ thuộc vị trí điểm đầu và điểm cuối của đường đi trong điện trường. Chọn D Câu hỏi 9 : Công của lực điện khi di chuyển một điện tích điểm \(q = {2.10^{ - 6}}C\) qua hiệu điện thế U= 2V có độ lớn là:
Đáp án: D Phương pháp giải: Công của lực điện: \(A = q.U\) Lời giải chi tiết: Công của lực điện có độ lớn là:\(A = q.U = {2.10^{ - 6}}.2 = {4.10^{ - 6}}J\) Chọn D. Câu hỏi 10 : Xác định công của lực điện khi di chuyên một electron từ điểm A đến điểm B trong điện trường. Biết hiệu điện thế giữa hai điểm AB là Uab = 5V.
Đáp án: A Phương pháp giải: Công thức liên hệ giữa công và hiệu điện thế A = qU Lời giải chi tiết: Cách giải: Áp dụng công thức A = q.U = (-1.6/10-19).5 = - 8.10-19J = - 5eV → Chọn A Câu hỏi 11 : Nếu điện tích dịch chuyển trong điện trường sao cho thế năng của nó tăng thì công của của lực điện trường
Đáp án: A Lời giải chi tiết: Nếu điện tích dịch chuyển trong điện trường sao cho thế năng của nó tăng thì công của của lực điện trường âm. Câu hỏi 12 : Nếu chiều dài đường đi của điện tích trong điện trường tăng 2 lần thì công của lực điện trường
Đáp án: A Lời giải chi tiết: Chưa đủ dữ kiện để xác định Câu hỏi 13 : Công thức xác định công của lực điện trường làm dịch chuyển điện tích q trong điện trường đều E là A = qEd, trong đó d là:
Đáp án: C Phương pháp giải: Lời giải chi tiết: Công thức xác định công của lực điện trường làm dịch chuyển điện tích q trong điện trường đều E là A = qEd, trong đó d là độ dài đại số của đoạn từ hình chiếu điểm đầu đến hình chiếu điểm cuối lên một đường sức, tính theo chiều đường sức điện. Câu hỏi 14 :
Đáp án: D Phương pháp giải: Lời giải chi tiết: Do cường độ điện trường vuông góc với đường dịch chuyển nên cường độ điện trường không sinh công Câu hỏi 15 : Một điện tích q chuyển động trong điện trường không đều theo một đường cong kín. Gọi công của lực điện trong chuyển động đó là A thì
Đáp án: D Lời giải chi tiết: Công của lực điện trường không phụ thuộc vào hình dạng đường đi mà chỉ phụ thuộc vào hình chiếu điểm đầu và điểm cuối lên một đường sức điện. Do đó với một đường cong kín thì điểm đầu và điểm cuối trùng nhau, nên công của lực điện trường trong trường hợp này bằng không. Một điện tích q chuyển động trong điện trường không đều theo một đường cong kín. Gọi công của lực điện trong chuyển động đó là A thì A = 0 trong mọi trường hợp. Câu hỏi 16 : Chọn câu sai. Công của lực điện trường làm dịch chuyển điện tích
Đáp án: A Lời giải chi tiết: Đáp án A Câu hỏi 17 : Một điện tích q > 0 di chuyển một đoạn d theo hướng của một đường sức của điện trường đều có cường độ điện trường E thì công của lực điện trường bằng.
Đáp án: B Phương pháp giải: Lời giải chi tiết: Công của lực điện trường A = qEd Câu hỏi 18 : Công cần thiết để hai hạt proton đến gần nhau 0,5m là bao nhiêu biết rằng lúc đầu chúng cách nhau 1m trong chân không?
Đáp án: C Phương pháp giải: Phương pháp: + Áp dụng biểu thức tính điện thế: \({V_M} = \frac{{{A_{M\infty }}}}{q} = k\frac{Q}{r}\) + Áp dụng biểu thức tính công: AMN = (VM – VN ).q Lời giải chi tiết: Hướng dẫn giải: Để hai hạt proton lại gần nhau hơn, ta có thể để một hạt proton đứng yên, còn proton kia di chuyển từ A đến B. Gọi O là vị trí của proton đứng yên, A là vị trí ban đầu của proton cần di chuyển, B là vị trí lúc sau khi di chuyển của proton đó. Ta có: \(OA = 1m;OB = 0,5m\) Điện thế do proton đứng yên tại O gây ra tại A và B là: + Tại A: \({V_A} = k\frac{q}{{{r_A}}} = {9.10^9}\frac{{1,{{6.10}^{ - 19}}}}{1} = 14,{4.10^{ - 10}}V\) + Tại B: \({V_B} = k\frac{q}{{{r_B}}} = {9.10^9}\frac{{1,{{6.10}^{ - 19}}}}{{0,5}} = 28,{8.10^{ - 10}}V\) Công của lực điện trường khi proton thứ hai di chuyển từ A đến B là: \(A = q({V_A} - {V_B}) = 1,{6.10^{ - 19}}(14,{4.10^{ - 10}} - 28,{8.10^{ - 10}}) = - 23,{04.10^{ - 29}}J\) Công của điện trường là công cản => Công cần thiết để di chuyển proton từ A đến B là: A’ = - A = 23,04.10-29J => Chọn C Câu hỏi 19 : Một proton nằm cách electron khoảng r = 0,5.10-10m trong chân không. Vận tốc tối thiểu của proton để nó thoát khỏi sức hút của electron là?
Đáp án: D Phương pháp giải: Phương pháp: + Áp dụng biểu thức tính thế năng tương tác tĩnh điện: \({\rm{W}} = k\frac{{{e^2}}}{r}\) + Áp dụng biểu thức tính động năng: \({\rm{W}} = \frac{1}{2}m{v^2}\) + Áp dụng định luật bảo toàn năng lượng Lời giải chi tiết: Hướng dẫn giải: Ta có: + Lúc đầu năng lượng của hệ là thế năng tương tác tĩnh điện: \({{\rm{W}}_1} = k\frac{{{e^2}}}{r}\) + Khi nó vừa thoát ra thì có vận tốc v, lúc này nó không chịu lực hút của electron nên lúc này hệ không còn thế năng tương tác mà chỉ có động năng: \({{\rm{W}}_2} = \frac{1}{2}m{v^2}\) Áp dụng định luật bảo toàn năng lượng, ta có: \({{\rm{W}}_1} = {{\rm{W}}_2} \leftrightarrow k\frac{{{e^2}}}{r} = \frac{1}{2}m{v_0}^2 \to {v_0} = \sqrt {\frac{{2{{\rm{e}}^2}}}{{m{\rm{r}}}}} = 3,{2.10^6}m/s\) => Chọn D Câu hỏi 20 : Một electron di chuyển được đoạn đường 1 cm, dọc theo một đường sức điện, dưới tác dụng của lực điện trong một điện trường đều có cường độ điện trường 1000 V/m. Hỏi công của lực điện có giá trị nào sau đây ?
Đáp án: D Phương pháp giải: Phương pháp : Công của lực điện: A = qEd = qEs.cosα Lời giải chi tiết: Cách giải : Dưới tác dụng của lực điện, electron di chuyển ngược chiều điện trường (tức ngược chiều đường sức điện). Ta có: \(\alpha = \left( {\overrightarrow F ,\overrightarrow d } \right) = {180^0} \Rightarrow A = {q_e}.E.s.\cos \alpha = - 1,{6.10^{ - 19}}{.1000.10^{ - 2}}.\cos 180 = 1,{6.10^{ - 18}}J\) Chọn D Quảng cáo
|