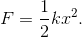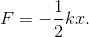40 bài tập con lắc lò xo mức độ thông hiểuLàm bàiQuảng cáo
Câu hỏi 1 : Phát biểu nào sai khi nói về dao động điều hòa của con lắc lò xo treo thẳng đứng?
Đáp án: D Phương pháp giải: Lời giải chi tiết: Đáp án D Câu hỏi 2 : Một con lắc lò xo dao động điều hòa với tần số 3 Hz. Động năng của con lắc biến thiên theo thời gian với tần số
Đáp án: D Phương pháp giải: Phương pháp: Động năng của con lắc lò xo biến thiên tuần hoàn theo thời gian với tần số bằng 2 lần tần số của dao động điều hòa. Lời giải chi tiết: Đáp án D f' = 2f = 2.3 = 6Hz Câu hỏi 3 : Một con lắc lò xo có độ cứng k = 150 N/m và có năng lượng dao động là E = 0,12 J. Biên độ dao động của con lắc có giá trị là
Đáp án: C Phương pháp giải: Sử dụng công thức tính cơ năng của con lắc đơn dao động điều hoà Lời giải chi tiết: Ta có: \(E = {{k{A^2}} \over 2} \Rightarrow A = \sqrt {{{2E} \over k}} = \sqrt {{{2.0,12} \over {150}}} = 0,04(m)\) Câu hỏi 4 : Một vật nhỏ dao động điều hòa với biên độ 5 cm và tốc độ cực đại là 10π cm/s. Chu kì dao động của vật nhỏ là:
Đáp án: C Phương pháp giải: Lời giải chi tiết: Phương pháp: Áp dụng công thức tính tốc độ cực đại của vật dao động điều hòa Ta có vmax = ωA => ω = vmax/A = 2π rad/s => Chu kì dao động: T = 2π/ω = 1 s => Chọn C Câu hỏi 5 : Một chất điểm dao động điều hòa với biên độ 10 cm và tần số góc 2 rad/s. Tốc độ cực đại của chất điểm là
Đáp án: A Phương pháp giải: Lời giải chi tiết: Phương pháp: Áp dụng công thức tính tốc độ cực đại của vật dao động điều hòa + Ta có vmax = ωA = 2.10 = 20 cm/s => Chọn A Câu hỏi 6 : Một con lắc lò xo có độ cứng 40 N/m dao động điều hòa với chu kỳ 0,1 s. Lấy π2= 10. Khối lượng vật nhỏ của con lắc là
Đáp án: A Phương pháp giải: Lời giải chi tiết: Câu hỏi 7 : Một con lắc lò xo dao động điều hòa với tần số 4 Hz. Thế năng của con lắc biến thiên theo thời gian với tần số
Đáp án: B Phương pháp giải: Lời giải chi tiết: Phương pháp: Thế năng của con lắc lò xo biến thiên tuần hoàn theo thời gian với tần số bằng 2 lần tần số của dao động điều hòa + f = 4Hz => tần số biến thiên theo thời gian của thế năng là 2f = 8Hz => Chọn B Câu hỏi 8 : Con lắc lò xo gồm vật có khối lượng m và lò xo có độ cứng k = 100 N/m. Vật thực hiện được 10 dao động trong 5 (s). Lấy π2 = 10, khối lượng m của vật là
Đáp án: B Phương pháp giải: - Chu kì dao động : thời gian vật thực hiện hết một dao động toàn phần - Áp dụng công thức tính chu kì dao động của con lắc lò xo Lời giải chi tiết: Vật thực hiện 10 dao động mất 5s nên chu kỳ dao động của vật là T = 0,5s Từ công thức xác định chu kỳ dao động của con lắc lò xo dao động điều hào ta có khối lượng của vật nhỏ là \(T = 2\pi \sqrt {\frac{m}{k}} \Rightarrow m = \frac{{{T^2}.k}}{{4{\pi ^2}}} = \frac{{{{0,5}^2}.100}}{{4.10}} = 0,625kg = 625g\)
Câu hỏi 9 : Một con lắc lò xo đang dao động điều hòa. Lực kéo về tác dụng vào vật nhỏ của con lắc có độ lớn tỉ lệ thuận với
Đáp án: B Phương pháp giải: Lời giải chi tiết: Lực kéo về tác dụng vào vật nhỏ của con lắc có độ lớn tỉ lệ thuận với độ lớn li độ của vật. Chọn B Câu hỏi 10 : Một con lắc lò xo gồm vật nhỏ và lò xo nhẹ có độ cứng k, dao động điều hòa dọc theo trục Ox quanh vị trí cân bằng O. Biểu thức lực kéo về tác dụng lên vật theo li độ x là
Đáp án: B Phương pháp giải: Lời giải chi tiết: Đáp án B Phương pháp : Biểu thức tính lực kéo về của con lắc lò xo F = - kx Câu hỏi 11 : Một con lắc lò xo dao động điều hòa theo phương ngang. Nếu biên đô dao động của con lắc tăng lên gấp đôi thì tần số dao động của con lắc:
Đáp án: B Phương pháp giải: Phương pháp: Sử dụng công thức về dao động điều hòa của con lắc lò xo. Lời giải chi tiết: Đáp án B Tần số dao động của con lắc lò xo:$$f = {\omega \over {2\pi }} = {1 \over {2\pi }}\sqrt {{k \over m}} $$ không phụ thuộc vào biên độ dao động của con lắc Câu hỏi 12 : Con lắc đơn có chiều dài 1 m, dao động điều hòa với tần số 0,5 Hz. Lấy π = 3,14. Gia tốc trọng trường tại nơi treo con lắc là:
Đáp án: C Phương pháp giải: Áp dụng công thức tính tần số trong dao động cơ.
Lời giải chi tiết: Đáp án C Tần số dao động của con lắc đơn: $$f = {\omega \over {2\pi }} = {1 \over {2\pi }}\sqrt {{g \over l}} \to g = 4{\pi ^2}{f^2}l$$ thay số ta được: $$g = {4.3,14^2}{.0,5^2}.1 = 9,86m/{s^2}$$ Câu hỏi 13 : Một con lắc lò xo treo thẳng đứng. Khi vật ở vị trí cân bằng lò xo giãn 4 cm. Kích thích cho vật nặng của con lắc dao động điều hòa theo phương thẳng đứng với biên độ 3 cm. Độ giãn cực đại của lò xo khi vật dao động là:
Đáp án: C Phương pháp giải: Vận dụng lí thuyết về dao động của con lắc lò xo treo thẳng đứng.
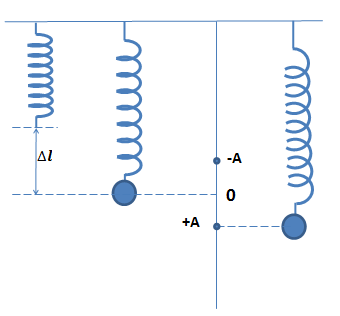
Lời giải chi tiết: Đáp án C Ta có: - Độ dãn lò xo tại vị trí cân bằng: $$\Delta {l_0} = {{mg} \over k} = 4cm$$ - Biên độ: A = 3cm Lò xo có độ giãn cực đại khi vật dao động ở vị trí +A Độ giãn của lò xo khi đó là:$$\Delta l = \Delta {l_0} + A = 4 + 3 = 7cm$$
Câu hỏi 14 : Con lắc lò xo nằm ngang dao động điều hòa với biên độ A. Khi vật nặng chuyển động qua vị trí cân bằng thì giữ cố định điểm chính giữa của lò xo. Vật sẽ tiếp tục dao động với biên độ dao động bằng
Đáp án: A Phương pháp giải: Áp dụng công thức bảo toàn năng lượng Lời giải chi tiết: Đáp án A + Khi vật đi qua vị trí cân bằng năng lượng cua con lắc bằng động năng E = Ed. → Giữ điểm chính giữa của lò xo, hệ dao động mới với lò xo có độ cứng gấp đôi. + Ta có E' = Ed = E → \(A' = {A \over {\sqrt 2 }}\) Câu hỏi 15 : Con lắc lò xo treo thẳng đứng, độ cứng k = 80 N/m, vật nặng khối lượng m = 200 g dao động điều hòa theo phương thẳng đứng với biên độ A = 5 cm, lấy g = 10 m/s2. Trong một chu kì T, thời gian lò xo giãn là
Đáp án: B Phương pháp giải: Đặc điểm của con lắc lò xo treo thẳng đứng ở vị trí cân bằng \(\Delta {l_0} = {{mg} \over k}\) Lời giải chi tiết: Đáp án B + Độ biến dạng của lò xo tại vị trí cân bằng \(\Delta {l_0} = {{mg} \over k} = 2,5\,cm\) Với A = 2Δl0 → thời gian lò xo giãn trong một chu kì là \(\Delta t = {{2T} \over 3} = {\pi \over {15}}s\) Câu hỏi 16 : Một con lắc lò xo có vật nặng khối lượng m. Nếu tăng khối lượng của vật thành 2m thì tần số dao động của vật là
Đáp án: D Phương pháp giải: Lời giải chi tiết: Đáp án D + Ta có \(f \sim {1 \over {\sqrt m }}\) → m tăng 2 lần thì \(f' = {f \over {\sqrt 2 }}\) Câu hỏi 17 : Một con lắc lò xo treo thẳng đứng, từ vị trí cân bằng O kéo con lắc về phía dưới theo phương thẳng đứng thêm 3 cm rồi thả nhẹ, con lắc dao động điều hòa quanh vị trí cân bằng O. Khi con lắc cách vị trí cân bằng 1 cm, tỷ số giữa thế năng và động năng của hệ dao động là
Đáp án: A Phương pháp giải: Phương pháp: Định luật bảo toàn cơ năng Lời giải chi tiết: Đáp án A + Tỉ số giữa động năng và thế năng tại vị trí có tọa độ x: $${{{E_t}} \over {{E_d}}} = {{{x^2}} \over {{A^2} - {x^2}}} = {{{1^2}} \over {{3^2} - {1^2}}} = {1 \over 8}$$. Câu hỏi 18 : Con lắc lò xo gồm vật nặng treo dưới lò xo dài, có chu kì dao động là T. Nếu lò xo bị cắt bớt 2/3 chiều dài thì chu kì dao động của con lắc mới là
Đáp án: D Phương pháp giải: Lời giải chi tiết: Đáp án D + Lò xo mới có độ cứng k' = 3k → \(T' = {T \over {\sqrt 3 }}\) Câu hỏi 19 : Một con lắc lò xo gồm vật nặng m = 1 kg gắn với một lò xo có khối lượng không đáng kể, độ cứng k = 100 N/m thực hiện dao động điều hòa. Tại thời điểm t = 1 s, vật có li độ x = 0,3 m và vận tốc v = - 4 m/s. Biên độ dao động của vật
Đáp án: C Phương pháp giải: Phương pháp: Áp dụng hệ thức độc lập giữa x, A, v ω : $$A = \sqrt {x_0^2 + {{\left( {{{{v_0}} \over \omega }} \right)}^2}} $$ Lời giải chi tiết: Đáp án C + Tần số góc của dao động $$\omega = \sqrt {{k \over m}} = 10 rad/s$$ → Biên độ dao động của vật $$A = \sqrt {{x^2} + {{\left( {{v \over \omega }} \right)}^2}} = 0,5m$$. Câu hỏi 20 : Vật có khối lượng m treo vào lò xo có độ cứng k. Kích thích cho vật dao động điều hòa với biên độ 3 cm thì chu kì dao động của nó là T = 0,3 s. Nếu kích thích cho vật dao động với biên độ bằng 6 cm thì chu kì dao động của con lắc là
Đáp án: A Phương pháp giải: Lời giải chi tiết: Đáp án A + Chu kì dao động của vật chỉ phụ thuộc vào đặc tính của hệ nên luôn là 0,3 s. Câu hỏi 21 : Một vật có khối lượng 0,4 kg được treo vào lò xo có độ cứng 80 N/m. Vật được kéo theo phương thẳng đứng ra khỏi vị trí cân bằng bằng một đoạn bằng 0,1 m rồi thả cho dao động. Tốc độ của vật khi qua vị trí cân bằng là
Đáp án: C Phương pháp giải: Lời giải chi tiết: Đáp án C + Tốc độ cực đại vmax = ωA = 1,4 m/s. Câu hỏi 22 : Một quả cầu khối lượng m treo vào một lò xo có độ cứng k làm lò xo dãn một đoạn 4cm. Kéo vật ra khỏi vị trí cân bằng theo phương thẳng đứng một đoạn và thả nhẹ. Lấy g = π2 m/s2 . Chu kỳ dao động của vật là :
Đáp án: D Phương pháp giải: Chu kì dao động của con lắc lò xo: \(T = 2\pi \sqrt {{g \over {\Delta l}}} \) Lời giải chi tiết: Ta có: \(T = 2\pi \sqrt {{{\Delta l} \over g}} = 2\pi \sqrt {{{{{4.10}^{ - 2}}} \over {{\pi ^2}}}} = 0,4s\) Chọn D Câu hỏi 23 : Một con lắc lò xo treo thẳng đứng gồm lò xo có độ cứng k, vật nặng có khối lượng m. Độ dãn của lò xo khi vật ở vị trí cân bằng là
Đáp án: D Phương pháp giải: Lời giải chi tiết: Đáp án D Độ giãn cua lò xo tại vị trí cân bằng $$\Delta l = {{mg} \over k}$$ Câu hỏi 24 : Con lắc lò xo dao động điều hòa theo phương nằm ngang. Khoảng thời gian giữa hai thời điểm liên tiếp động năng bằng thế năng là 0,2 s. Chu kì dao động của con lắc là:
Đáp án: D Phương pháp giải: Lời giải chi tiết: Đáp án D Khoảng thời gian giữa hai lần động năng là $$\Delta t = {T \over 4} = 0,2 = > T = 0,8s$$ Câu hỏi 25 : Một vật m = 5 kg được treo vào một lò xo. Vật dao động điều hòa với T = 0,5 s. Chiều dài lò xo sẽ thu ngắn lại một đoạn bao nhiêu kể từ vị trí cân bằng nếu người ta bỏ vật đi?
Đáp án: D Phương pháp giải: Lời giải chi tiết: Đáp án D + Lò xo sẽ thu ngắn một đoạn Δl0 với $$T = 2\pi \sqrt {{{\Delta {l_0}} \over g}} \Rightarrow \Delta {l_0} = 6,2 cm $$. Câu hỏi 26 : Một con lắc lò xo dao động điều hòa theo phương thẳng đứng, ở vị trí cân bằng lò xo dãn một đoạn x0. Hợp lực của trọng lực và lực đàn hồi tác dụng vào vật có độ lớn bằng trọng lực khi vật ở vị trí
Đáp án: A Phương pháp giải: Lời giải chi tiết: Đáp án A + Một con lắc lò xo dao động điều hòa theo phương thẳng đứng, ở vị trí cân bằng lò xo dãn một đoạn x0. Hợp lực của trọng lực và lực đàn hồi tác dụng vào vật có độ lớn bằng trọng lực khi vật ở vị trí mà lò xo có độ dãn bằng 2x0. Câu hỏi 27 : Một con lắc lò xo treo theo phương thẳng đứng dao động điều hòa với biên độ 4 cm. Khi vật ở vị trí lò xo dãn 2 cm thì động năng bằng ba lần thế năng. Khi lò xo dãn 6 cm thì
Đáp án: B Phương pháp giải: Phương pháp: Áp dụng định luật bảo toàn năng lượng Lời giải chi tiết: Đáp án B + Ta có: A = 4 cm + Khi động năng bằng ba lần thế năng $$ = > \left| x \right| = {A \over 2} = 2cm$$ + Khi lò xo dãn 6 cm$$ = > A + \left| x \right| = 6cm = > \left| x \right| = 2cm = {A \over 2}$$ → Động năng bằng ba lần thế năng Câu hỏi 28 : Một con lắc lò xo gồm quả nặng khối lượng 1 kg và một lò xo có độ cứng 1600 N/m. Khi quả nặng ở VTCB, người ta truyền cho nó vận tốc ban đầu bằng 2 m/s. Biên độ dao động của quả nặng là:
Đáp án: D Phương pháp giải: vmax = ωA Lời giải chi tiết: Vận tốc của vật ở VTCB: \({v_{m{\rm{ax}}}} = \omega A = \sqrt {{k \over m}} .A \Rightarrow A = {v_{m{\rm{ax}}}}\sqrt {{m \over k}} = 2.\sqrt {{1 \over {1600}}} = 5cm\) Câu hỏi 29 : Một con lắc lò xo treo thẳng đứng (m = 250 g, k = 100 N/m). Kéo vật xuống dưới theo phương thẳng đứng đến vị trí lò xo dãn 7,5 cm rồi thả nhẹ. Chọn gốc tọa độ ở vị trí cân bằng, trục tọa độ thẳng đứng, chiều dương hướng lên, gốc thời gian là lúc thả vật. Lấy g = 10 m/s2. Phương trình dao động của vật là
Đáp án: C Phương pháp giải: Phương pháp: Đại cương về dao động cơ học. Lời giải chi tiết: Đáp án C + Ta có: m = 250 g, k = 100 N/m, ω = 20 rad/s. →$$\Delta l = {{mg} \over k} = 0,025m = 2,5cm$$ +Kéo vật xuống dưới theo phương thẳng đứng đến vị trí lò xo dãn 7,5 cm rồi thả nhẹ => A = 7,5 – Δl = 5 cm Trục tọa độ Ox thẳng đứng, hướng lên, gốc thời gian là lúc thả vật => t = 0 : x = -A => φ = π →Phương trình dao động của vật là x = 5cos(20t + π) cm Câu hỏi 30 : Một con lắc lò xo gồm vật nhỏ và lò xo nhẹ có độ cứng k, dao động điều hòa dọc theo trục Ox quanh vị trí cân bằng O. Biểu thức lực kéo về theo li độ x là
Đáp án: B Phương pháp giải: Lời giải chi tiết: Biểu thức lực kéo về trong dao động điều hòa của con lắc lò xo là F = - kx Chọn B Câu hỏi 31 : Một con lắc đơn có chiều dài 1 m dao động với α0 = 300 tại nơi có g = 9,8 m/s2. Vận tốc của con lắc khi qua vị trí cân bằng có giá trị là
Đáp án: B Phương pháp giải: Phương pháp : Áp dụng công thức tính vận tốc của con lắc đơn
$$v = \sqrt {2gl\left( {cos\alpha - \cos {\alpha _0}} \right)} $$ Lời giải chi tiết: + Vận tốc của con lắc khi đi qua vị trí cân bằng $$v = \sqrt {2gl\left( {cos 1 - \cos {\alpha _0}} \right)}=1,62 m/s $$ Câu hỏi 32 : Một con lắc lò xo dao động điều hòa theo phương thẳng đứng. Phát biểu nào sau đây là SAI?
Đáp án: A Phương pháp giải: Lời giải chi tiết: Đáp án A Câu hỏi 33 : Một con lắc lò xo gồm lò xo có khối lượng không đáng kể, có độ cứng k = 100 N/m, khối lượng của vật kg. Kéo vật khỏi vị trí cân bằng x = +3 cm, và truyền cho vật vận tốc v = 30 cm/s, ngược chiều dương, chọn t = 0 là lúc vật bắt đầu chuyển động. Phương trình dao động của vật là
Đáp án: C Phương pháp giải: Phương pháp: Áp dụng hệ thức độc lập giữa x, A, v ω : $$A = \sqrt {x_0^2 + {{\left( {{{{v_0}} \over \omega }} \right)}^2}} $$ Lời giải chi tiết: Đáp án C + Tần số góc của dao động $$\omega = \sqrt {{k \over m}} = 10 rad/s $$. + Biên độ dao động của vật $$A = \sqrt {x_0^2 + {{\left( {{{{v_0}} \over \omega }} \right)}^2}} = 3\sqrt 2 \,cm$$ Ban đầu vật đi qua vị trí có li độ $$x = {{\sqrt 2 } \over 2}A$$ theo chiều âm → φ0 = 0,25π rad. → $$x = 3\sqrt 2 \cos \left( {10t + {\pi \over 4}} \right) cm$$. Câu hỏi 34 : Người ta làm thí nghiệm với một con lắc lò xo treo thẳng đứng: Lần 1, cung cấp cho vật vận tốc v0 khi vật ở vị trí cân bằng thì vật dao động điều hòa với biên độ A1; lần 2, đưa vật đến vị trí cách vị trí cân bằng x0 rồi buông nhẹ thì vật dao động điều hòa với biên độ A2; lần 3, đưa vật đến vị trí cách vị trí cân bằng x0 rồi cung cấp cho vật vận tốc v0 thì vật dao động điều hòa với biên độ
Đáp án: B Phương pháp giải: Lời giải chi tiết: Đáp án B + Biên độ dao động A1 là \({A_1} = {{{v_0}} \over \omega }\) + Biên độ dao động A2 là: A2 = x0. + Biên độ dao động A3 là \({A_3} = \sqrt {x_0^2 + {{\left( {{{{v_0}} \over \omega }} \right)}^2}} = \sqrt {A_1^2 + A_2^2} \) Câu hỏi 35 : Gắn vật nặng có khối lượng m = 81 g vào một lò xo lí tưởng thì tấn số dao động của vật là 10 Hz. Gắn thêm một gia trọng có khối lượng Δm = 19 g vào vật m thì tần số dao động của hệ bằng:
Đáp án: D Phương pháp giải: Phương pháp: Áp dụng công thức tính tần sô trong con lắc lò xo Lời giải chi tiết: Đáp án D Câu hỏi 36 : Hai con lắc lò xo có cùng độ cứng k. Biết chu kỳ dao động T1 = 2T2. Khối lượng của hai con lắc liên hệ với nhau theo công thức:
Đáp án: B Phương pháp giải: Phương pháp: Áp dụng công thức tính chu kỳ của vật. Lời giải chi tiết: Đáp án B $${{{T_1}} \over {{T_2}}} = \sqrt {{{{m_1}} \over {{m_2}}}} = {1 \over 2}$$ Câu hỏi 37 : Một con lắc lò xo gồm: vật m và lò xo có độ cứng k = 20 N/m dao động với chu kì 2 s. Tính khối lượng m của vật dao động. Lấy π2 =10.
Đáp án: B Phương pháp giải: Phương pháp: Áp dụng công thức tính chu kỳ của con lắc lò xo.
Lời giải chi tiết: Đáp án B Câu hỏi 38 : Một con lắc lò xo thẳng đứng có khối lượng m và có độ cứng của lò xo là k. Nếu tăng độ cứng của lò xo lên 2 lần đồng thời giảm khối lượng m đi 8 lần thì tần số dao động điều hòa của vật sẽ.
Đáp án: B Phương pháp giải: Áp dụng công thức tính tần số dao động của con lắc lò xo Lời giải chi tiết: Tần số dao động của con lắc lò xo được tính theo công thức \(f = {1 \over {2\pi }}\sqrt {{k \over m}} \) Theo đề bài ta có \({{f'} \over f} = \sqrt {{{k'} \over k}.{m \over {m'}}} = \sqrt {{{2k} \over k}.{m \over {{m \over 8}}}} = 4\) Vậy tần số dao động tăng lên 4 lần. Chọn B Câu hỏi 39 : Một con lắc lò xo gồm lò xo có độ cứng k, vật nhỏ khối lượng 100 g, dao động điều hòa với tần số góc 20 rad/s. Giá trị của k là
Đáp án: C Phương pháp giải: Lời giải chi tiết: Đáp án C Giá trị độ cứng k của lò xo được xác định bởi biểu thức \(k = {\omega ^2}m = {20^2}.0,1 = 40\,N/m\) Câu hỏi 40 : Một con lắc lò xo treo thẳng đứng, độ cứng k = 100N/m, vật nặng khối lượng m = 250g. Khi vật cân bằng lò xo dãn:
Đáp án: C Phương pháp giải: Phương pháp: Áp dụng công thức tính độ dãn của con lắc lò xo đứng khi ở vị trí cân bằng \(\Delta l = \frac{{mg}}{k}\) Lời giải chi tiết: Đáp án C Áp dụng công thức tính độ dãn của con lắc lò xo đứng khi ở vị trí cân bằng \(\Delta l = \frac{{mg}}{k} = \frac{{0,25.10}}{{100}} = 0,025m = 2,5cm\) Quảng cáo
|