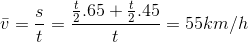15 bài tập Chuyển động cơ mức độ vận dụng

Câu hỏi 1 :

Một xe chuyển động từ A về B. Nửa thời gian đầu vận tốc của xe là v₁, nửa thời gian sau vận tốc của xe là v₂. Tính vận tốc trung bình của xe trên cả quãng đường AB.

A $v = \frac{{{v_1} + {v_2}}}{2}$
B $v = \frac{{{v_1}{v_2}}}{{{v_1} + {v_2}}}$
C $v = \frac{{{v_1}{v_2}}}{{2\left( {{v_1} + {v_2}} \right)}}$
D $v = \frac{{2{v_1}{v_2}}}{{2{v_1} + 3{v_2}}}$

Đáp án: A

Phương pháp giải:

Phương pháp : Áp dụng công thức tính vận tốc trung bình ${v_{tb}} = \frac{{{S_1} + {S_2}}}{{{t_1} + {t_2}}}$

Lời giải chi tiết:

Cách giải

Gọi t là tổng thời gian xe chuyển động từ A về B, v là vận tốc trung bình của xe.

Độ dài quãng đường AB là: S = v.t (1)

Theo bài ta có: S = ${v_1}.\frac{t}{2} + {v_2}.\frac{t}{2}$ (2)

$ \Rightarrow $ v.t = ${v_1}.\frac{t}{2} + {v_2}.\frac{t}{2}$$ \Rightarrow v = \frac{{{v_1} + {v_2}}}{2}$

Chọn A

Đáp án - Lời giải

Câu hỏi 2 :

Một xe chuyển động từ A về B. Nửa quãng đường đầu vận tốc của xe là v₁, nửa quãng đường sau vận tốc của xe là v₂. Tính vận tốc trung bình của xe trên cả quãng đường.

A $v = \frac{{2{v_1}{v_2}}}{{{v_1} + {v_2}}}$
B $v = \frac{{{v_1}{v_2}}}{{{v_1} + {v_2}}}$
C $v = \frac{{{v_1}{v_2}}}{{2\left( {{v_1} + {v_2}} \right)}}$
D $v = \frac{{2{v_1}{v_2}}}{{2{v_1} + 3{v_2}}}$

Đáp án: A

Phương pháp giải:

Phương pháp : Áp dụng công thức tính vận tốc trung bình ${v_{tb}} = \frac{{{S_1} + {S_2}}}{{{t_1} + {t_2}}}$

Lời giải chi tiết:

Cách giải

Gọi S là độ dài quãng đường AB, gọi v là vận tốc trung bình của xe trên cả quãng đường AB.

Thời gian đi từ A về B là t = $\frac{S}{v}$ (1)

Mặt khác, theo bài ra ta có t = $\frac{{{S_{}}}}{{2{v_1}}} + \frac{S}{{2{v_2}}}$ (2)

Từ (1) và (2) ta có: $\frac{S}{v} = \frac{S}{{2{v_1}}} + \frac{S}{{2{v_2}}} \Rightarrow v = \frac{{2{v_{1.}}{v_2}}}{{{v_1} + {v_2}}}$

Chọn A

Đáp án - Lời giải

Câu hỏi 3 :

Một xe chuyển động từ A về B. Vận tốc của xe trong $\frac{1}{3}$ quãng đường đầu là v₁ = 40km/h, trong $\frac{1}{3}$ quãng đường tiếp theo là v₂ = 60km/h và vận tốc trên quãng đường còn lại là v₃ = 30km/h. Tính vận tốc trung bình của xe trên cả quãng đường.

A $v = 40km/h$
B $v = 35km/h$
C $v = 36km/h$
D $v = 34km/h$

Đáp án: A

Phương pháp giải:

Vận tốc trung bình: ${{v}_{tb}}=\frac{{{S}_{1}}+{{S}_{2}}+{{S}_{3}}}{{{t}_{1}}+{{t}_{2}}+{{t}_{3}}}$

Lời giải chi tiết:

Gọi S là độ dài quãng đường AB, gọi v là vận tốc trung bình của xe trên cả quãng đường AB.

Thời gian đi từ A về B là: $t=\frac{S}{v}\,\,(1)$

Mặt khác, theo bài ra ta có:

$t=\frac{S}{3{{v}_{1}}}+\frac{S}{3{{v}_{2}}}+\frac{S}{3{{v}_{3}}}=\frac{S}{120}+\frac{S}{180}+\frac{S}{90}=\frac{S}{40}\,\,\,(2)$

Từ (1) và (2) ta có:

$\frac{S}{v}=\frac{S}{40}\Rightarrow v=40km/h$

Chọn A.

Đáp án - Lời giải

Câu hỏi 4 :

Một xe chuyển động từ A về B. Vận tốc của xe trong $\frac{1}{3}$ quãng đường đầu là v₁ = 40km/h, trong $\frac{1}{3}$ quãng đường tiếp theo là v₂ = 60km/h và vận tốc trên quãng đường còn lại là v₃. Tính v₃ biết vận tốc trung bình của xe trên cả quãng đường là v = 40km/h.

A $v = 34km/h$
B $v = 35km/h$
C $v = 36km/h$
D $v = 30km/h$

Đáp án: D

Phương pháp giải:

Vận tốc trung bình: ${{v}_{tb}}=\frac{{{S}_{1}}+{{S}_{2}}+{{S}_{3}}}{{{t}_{1}}+{{t}_{2}}+{{t}_{3}}}$

Lời giải chi tiết:

Gọi S là độ dài quãng đường AB, gọi v là vận tốc trung bình của xe trên cả quãng đường AB.

Thời gian đi từ A về B là: $t=\frac{S}{v}=\frac{S}{40}\,\,\,(1)$

Mặt khác, theo bài ra ta có:

$t=\text{ }\frac{S}{3{{v}_{1}}}+\frac{S}{3{{v}_{2}}}+\frac{S}{3{{v}_{3}}}=\frac{S}{120}+\frac{S}{180}+\frac{S}{3.{{v}_{3}}}=\frac{S}{72}+\frac{S}{3.{{v}_{3}}}\,\,\,(2)$

Từ (1) và (2) ta có:

$\frac{S}{40}=\frac{S}{72}+\frac{S}{3.{{v}_{3}}}\Rightarrow {{v}_{3}}=30km/h$

Chọn D.

Đáp án - Lời giải

Câu hỏi 5 :

Vòng chạy quanh sân trường dài 400m. Học sinh chạy thi cùng xuất phát từ một điểm. Biết vận tốc của các em lần lượt v₁ = 4,8m/s và v₂ = 4m/s; Tính thời gian ngắn nhất để hai em gặp nhau trên đường chạy

A t = 8 phút 30s
B t = 7 phút 20s
C t = 7 phút 30s
D t = 8 phút 20s

Đáp án: D

Phương pháp giải:

Công thức tính thời gian: $t=\frac{S}{v}$

Lời giải chi tiết:

Vì em thứ nhất chạy nhanh hơn em thứ hai nên trong một giây em thứ nhất vượt xa em thứ hai một đoạn đường là: ${{S}_{1}}~{{S}_{2}}~=0,8m$

Em thứ nhất muốn gặp em thứ hai trong khoảng thời gian ngắn nhất thì em thứ nhất phải vượt em thứ hai đúng 1 vòng sân.

Vậy thời gian ngắn nhất để hai em gặp nhau trên đường chạy: $t=\frac{400}{0,8}=500\text{s}=8phut20s$

Chọn D.

Đáp án - Lời giải

Câu hỏi 6 :

Một vật chuyển động không đều. Biết vận tốc trung bình của vật trong 1/3 thời gian đầu bằng 12m/s; trong thời gian còn lại bằng 9m/s. Vận tốc trung bình của vật trong suốt thời gian chuyển động là

A 10,5m/s
B 10m/s
C 9,8m/s
D 11 m/s

Đáp án: B

Phương pháp giải:

Phương pháp : Áp dụng công thức tính vận tốc trung bình ${v_{tb}} = \frac{{{S_1} + {S_2}}}{{{t_1} + {t_2}}}$

Lời giải chi tiết:

Cách giải:

Ta có:

$\left. \begin{array}{l}{S_1} = {v_1}.{t_1} = 12\frac{t}{3} = 4t\\{S_2} = {v_2}.{t_2} = 9.\frac{2}{3}t = 6t\,\end{array} \right\rangle = > {v_{tb}} = \frac{{{s_1} + {s_2}}}{t} = \frac{{10t}}{t} = 10m/s$

Chọn B

Đáp án - Lời giải

Câu hỏi 7 :

Một người đi bộ đều trên quãng đường đầu dài 3km với vận tốc 2m/s. Quãng đường tiếp theo dài 1,95km, người đó đi hết 0,5h. Tính vận tốc trung bình của người đó trên cả hai quãng đường.

A 2 m/s
B 1,5m/s
C 1m/s
D 2,5m/s

Đáp án: B

Phương pháp giải:

Phương pháp : Áp dụng công thức tính vận tốc trung bình ${v_{tb}} = \frac{{{S_1} + {S_2}}}{{{t_1} + {t_2}}}$

Lời giải chi tiết:

Cách giải:

Vận tốc trung bình trên cả quãng đường:

${t_1} = \frac{{{S_1}}}{{{v_1}}} = \frac{{3000}}{2} = 1500{\rm{s = > }}v = \frac{{{S_1} + {S_2}}}{{{t_1} + {t_2}}} = \frac{{3000 + 1950}}{{1500 + 1800}} = 1,5m/s$

Chọn B

Đáp án - Lời giải

Câu hỏi 8 :

Một ôtô chuyển động từ A đến B. Trong nữa thời gian đầu ôtô chuyển động với tốc độ 65 km/h, trong nữa thời gian sau ôtô chuyển động với tốc độ 45 km/h. Tốc độ trung bình trên cả quãng đường là

A 55km/h
B 50km/h
C 48km/h
D 45km/h

Đáp án: A

Lời giải chi tiết:

áp dụng công thức tính vận tốc trung bình ta có

$\bar{v}=\frac{s}{t}=\frac{\frac{t}{2}.65+\frac{t}{2}.45}{t}= 55km/h$

Đáp án - Lời giải

Câu hỏi 9 :

Tàu Thống nhất Bắc Nam S1 xuất phát từ ga Hà Nội vào lúc 19h00min, tới ga Vinh vào lúc 0h34min ngày hôm sau. Khoảng thời gian tàu Thống nhất Bắc Nam S1 chạy từ ga Hà Nội tới ga Vinh là

A 5h34min
B 24h34min
C 4h26min
D 18h26min

Đáp án: A

Phương pháp giải:

Khoảng thời gian: $\Delta t={{t}_{2}}-{{_{1}}$

Lời giải chi tiết:

Ta đổi: 00h34min thành 24h34min cùng ngày

Khi đó:

$\left\{ \begin{array}{l}
{t_1} = 19h00\min \\
{t_2} = 24h34\min
\end{array} \right.$

Khoảng thời gian mà tàu chạy là:

$\Delta t=24h34min19h00min=5h34min$

Chọn A.

Đáp án - Lời giải

Câu hỏi 10 :

Biết giờ Bec Lin (Cộng hoà liên bang Đức) chậm hơn giờ Hà Nội 6 giờ, trận chung kết bóng đá Wold Cup năm 2006 diễn ra tại Bec Lin vào lúc 19h00min ngày 9 tháng 7 năm 2006 giờ Bec Lin. Khi đó giờ Hà Nội là

A 1h00min ngày 10 tháng 7 năm 2006
B 13h00min ngày 9 tháng 7 năm 2006
C 1h00min ngày 9 tháng 7 năm 2006
D 13h00min ngày 10 tháng 7 năm 2006

Đáp án: A

Phương pháp giải:

Lời giải chi tiết:

Trận chung kết bóng đá Wold Cup năm 2006 diễn ra tại Bec Lin vào lúc 19h00min ngày 9 tháng 7 năm 2006 giờ Bec Lin.

Giờ Hà Nội chạy nhanh hơn Bec lin là 6h nên khi đó giờ Hà Nội là:

1h00min ngày 10 tháng 7 năm 2006.

Chọn A.

Đáp án - Lời giải

Câu hỏi 11 :

Một vận động viên đua xe đạp vô địch thế giới đã thực hiện cuộc đua vượt đèo với kết quả như sau (H.3.2):

Quãng đường từ A đến B: 45km trong 2 giờ 15 phút.

Quãng đường từ B đến c : 30km trong 24 phút.

Quãng đường từ c đến D : 10km trong 1/4 giờ.

Hãy tính:

a) Vận tốc trung bình trên mỗi quãng đường.

b) Vận tốc trung bình trên cả quãng đường đua

A
a) Vận tốc trung bình trên mỗi quãng đường:5,56m/s; 20,83m/s; 11,1 m/s

b) Vận tốc trung bình trên cả quãng đường: Vtb = 8,24 m/s
B
a) Vận tốc trung bình trên mỗi quãng đường:5,56m/s; 20,83m/s; 11,1 m/s

b) Vận tốc trung bình trên cả quãng đường: Vtb = 8,14 m/s
C
a) Vận tốc trung bình trên mỗi quãng đường:4,56m/s; 22,83m/s; 11,1 m/s

b) Vận tốc trung bình trên cả quãng đường: Vtb = 8,14 m/s
D
a) Vận tốc trung bình trên mỗi quãng đường:5m/s; 20,83m/s; 11 m/s

b) Vận tốc trung bình trên cả quãng đường: Vtb = 8,14 m/s

Đáp án: B

Phương pháp giải:

Phương pháp : Áp dụng công thức tính vận tốc trung bình ${v_{tb}} = \frac{{{S_1} + {S_2}}}{{{t_1} + {t_2}}}$

Lời giải chi tiết:

Cách giải

a) Vận tốc trung bình trên mỗi quãng đường:5,56m/s; 20,83m/s; 11,1 m/s

b) Vận tốc trung bình trên cả quãng đường: Vtb = 8,14 m/s

Chọn B

Đáp án - Lời giải

Câu hỏi 12 :

Một xe chuyển động từ A để về B, khoảng cách AB là 63 km. Ban đầu xe chuyển động đều với vận tốc 60km/h. Sau đó, vì đường khó đi nên vận tốc của xe thay đổi liên tục, lúc thì 54km/h, lúc thì 45km/h....Khi về đến B vận tốc của xe giảm chỉ còn 10km/h. Vì vậy, thời gian xe đã chạy là 1h45’. Tính vận tốc trung bình của xe trên quãng đường AB.

A $v = 30km/h$
B $v = 35km/h$
C $v = 36km/h$
D $v = 34km/h$

Đáp án: C

Phương pháp giải:

Vận tốc trung bình: ${{v}_{tb}}=\frac{{{S}_{1}}+{{S}_{2}}+{{S}_{3}}}{{{t}_{1}}+{{t}_{2}}+{{t}_{3}}}$

Lời giải chi tiết:

Khoảng cách AB: S = 45km

Thời gian xe đi từ A đến B: $t=1h45'=1,75h$

Vận tốc trung bình của xe trên quãng đường AB:

$v=\frac{S}{t}=\frac{63}{1,75}=36km/h$

Chọn C.

Đáp án - Lời giải

Câu hỏi 13 :

Một ôtô chuyển động từ A về B. Chặng đầu xe đi mất $\frac{1}{3}$ tổng thời gian với vận tốc v₁ = 45km/h. Chặng giữa xe đi mất $\frac{1}{2}$ tổng thời gian với vận tốc v₂ = 60km/h. Chặng còn lại xe chuyển động với vận tốc v₃ = 48km/h. Tính vận tốc của xe trên cả quãng đường AB.

A $v = 40km/h$
B $v = 53km/h$
C $v = 46km/h$
D $v = 54km/h$

Đáp án: B

Phương pháp giải:

Vận tốc trung bình ${{v}_{tb}}=\frac{{{S}_{1}}+{{S}_{2}}+{{S}_{3}}}{{{t}_{1}}+{{t}_{2}}+{{t}_{3}}}$

Lời giải chi tiết:

Gọi t là tổng thời gian xe chuyển động từ A về B, v là vận tốc trung bình của xe.

Thời gian xe đi hết chặng cuối là: $t-\frac{t}{3}-\frac{t}{2}=\frac{t}{6}$

Độ dài quãng đường AB là: $S=v.t~\text{ }\,\,\,\left( 1 \right)$

Theo bài ta có: $S={{v}_{1}}.\frac{t}{3}+{{v}_{2}}.\frac{t}{2}+{{v}_{3}}.\frac{t}{6}=45.\frac{t}{3}+60.\frac{t}{2}+48\frac{t}{6}=53t\,\,\,(2)$

Từ (1) và (2) suy ra: $v.t=53t\Rightarrow v=53km/h$

Chọn B.

Đáp án - Lời giải

Câu hỏi 14 :

Một ôtô chuyển động từ A về B. Chặng đầu xe đi mất $\frac{1}{5}$ tổng thời gian với vận tốc v₁. Chặng giữa xe đi mất $\frac{1}{4}$ tổng thời gian với vận tốc v₂ = 60km/h. Chặng còn lại xe chuyển động với vận tốc v₃ = 40km/h. Biết vận tốc của xe trên cả quãng đường AB là v = 47 km/h. Tính v_1.

A ${v_1} = 40km/h$
B ${v_1} = 53km/h$
C ${v_1} = 50km/h$
D ${v_1} = 54km/h$

Đáp án: C

Phương pháp giải:

Vận tốc trung bình ${{v}_{tb}}=\frac{{{S}_{1}}+{{S}_{2}}+{{S}_{3}}}{{{t}_{1}}+{{t}_{2}}+{{t}_{3}}}$

Lời giải chi tiết:

Gọi t là tổng thời gian xe chuyển động từ A về B, v là vận tốc trung bình của xe.

Thời gian xe đi hết chặng cuối là: $t-\frac{t}{5}-\frac{t}{4}=\frac{11}{20}t$

Độ dài quãng đường AB là: $S=v.t=47t\,\,\text{ }\left( 1 \right)$

Theo bài ta có:

$S={{v}_{1}}.\frac{t}{3}+{{v}_{2}}.\frac{t}{2}+{{v}_{3}}.\frac{t}{6}={{v}_{1}}.\frac{t}{5}+60.\frac{t}{4}+40\frac{11t}{20}={{v}_{1}}.\frac{t}{5}+37t\,\,\,(2) $

$\Rightarrow 47.t={{v}_{1}}.\frac{t}{5}+37t\Rightarrow {{v}_{1}}=50km/h$

Chọn C.

Đáp án - Lời giải

Câu hỏi 15 :

Kỉ lục thế giới về chạy 100m do lực sĩ Tim — người Mĩ — đạt được là 9,86 giây

a) Chuyển động của vận động viên này trong cuộc đua là đều hay không đều ? Tại sao ?

b) Tính vận tốc trung bình của vận động viên này ra m/s và km/h.

A
a) Chuyển động của vận động viên này trong cuộc đua là không đều

b) ${v_{tb}} = \frac{s}{t} \approx 10,14m/s \approx 36,5km/h$
B
a) Chuyển động của vận động viên này trong cuộc đua là đều

b) ${v_{tb}} = \frac{s}{t} \approx 10,14m/s \approx 36,5km/h$
C
a) Chuyển động của vận động viên này trong cuộc đua là không đều

b) ${v_{tb}} = \frac{s}{t} \approx 15,22m/s \approx 54,8km/h$
D
a) Chuyển động của vận động viên này trong cuộc đua là đều

b) ${v_{tb}} = \frac{s}{t} \approx 15,22m/s \approx 54,8km/h$

Đáp án: A

Phương pháp giải:

Phương pháp : Áp dụng công thức tính vận tốc trung bình ${v_{tb}} = \frac{{{S_1} + {S_2}}}{{{t_1} + {t_2}}}$

Lời giải chi tiết:

Cách giải:

a) Không đều

b) ${v_{tb}} = \frac{s}{t} \approx 10,14m/s \approx 36,5km/h$

Chọn A

Đáp án - Lời giải

15 bài tập Chuyển động cơ mức độ vận dụng

15 bài tập Chuyển động cơ mức độ thông hiểu