Đề số 5 - Đề kiểm tra học kì 2 (Đề thi học kì 2) - Toán 12Đáp án và lời giải chi tiết Đề số 5 - Đề kiểm tra học kì 2 (Đề thi học kì 2) - Toán học 12 Quảng cáo
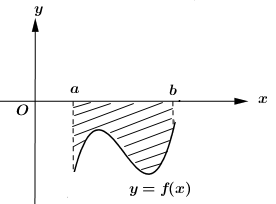
Đề bài Câu 1: Cho số phức \(z = 5 - 2i\). Phần ảo của số z bằng: A. 3. B. 4. C. 11. D. \( - 2\). Câu 2: Cho hàm số \(f\left( x \right)\) liên tục trên đoạn \(\left[ {a;b} \right]\). Khi quay hình dạng phẳng như hình vẽ xung quanh trục Ox ta được khối tròn xoay có thể tính là:
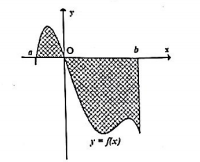
A. \(\pi \int\limits_a^b {{{\left[ {f\left( x \right)} \right]}^2}dx} .\) B. \(\int\limits_a^b {{{\left[ {f\left( x \right)} \right]}^2}dx} .\) C. \( - \pi \int\limits_a^b {{{\left[ {f\left( x \right)} \right]}^2}dx} .\) D. \( - \int\limits_a^b {f\left( x \right)dx} .\) Câu 3: \(\int {\frac{1}{{{\sin }^2}x}}dx} \) bằng A. \( - \cot x + C.\) B. \(\cot x + C.\) C. \( - \frac{1}{{\sin x}} + C.\) D. \(\tan x + C.\) Câu 4: \(\int\limits_1^2 {\left( {2x + 1 + \frac{1}{x}} \right)dx} \) bằng A. \(4 - \ln 2.\) B. \(4\ln 2.\) C. \(4 + \ln 2.\) D. 4. Câu 5: Trong không gian Oxyz, mặt cầu có tâm là \(I\left( {2; - 2;1} \right)\) và đi qua gốc tọa độ O thì có bán kính bằng A. 9. B. \(\sqrt 3 \) C. 3. D. 1. Câu 6: Trong không gian Oxyz, cho hai điểm \(A\left( {1;2; - 3} \right);\,\,B\left( {5; - 4;1} \right)\). Trung điểm đoạn AB có tọa độ là A. \(\left( {3; - 1; - 1} \right).\) B. \(\left( {3; - 1;1} \right).\) C. \(\left( {2; - 3;2} \right)\) D. \(\left( {3;1; - 1} \right)\) Câu 7: \(\int {{x^\pi }dx} \) bằng A. \({x^\pi } + C.\) B. \(\pi {x^{\pi - 1}} + C.\) C. \(\frac{{{x^\pi }}}{{\ln \pi }} + C.\) D. \(\frac{{{x^{\pi + 1}}}}{{\pi + 1}} + C.\) Câu 8: Cho số phức z có điểm biểu diễn hình học trong mặt phẳng tọa độ Oxy là điểm \(M\left( {3; - 4} \right)\). Môđun của z bằng A. 25. B. 5. C. 1. D. \(\sqrt 5 \) Câu 9: Trong không gian Oxyz, đường thẳng \(d:\left\{ \begin{array}{l}x = 2 + t\\y = - 1 + 3t\\z = 3\end{array} \right.\) có một vecto chỉ phương là A. \(\overrightarrow {{u_3}} = \left( {1;3;3} \right).\) B. \(\overrightarrow {{u_4}} = \left( {2; - 1;0} \right).\) C. \(\overrightarrow {{u_2}} = \left( {1;3;0} \right).\) D. \(\overrightarrow {{u_1}} = \left( {2; - 1;3} \right).\) Câu 10: Cho số phức \(z = 3 + 2i\). Giá trị của \(z.\overline z \) bằng A. 5. B. 9. C. 13. D. \(\sqrt {13} \). Câu 11: Trong không gian Oxyz, cho hai vecto \(\overrightarrow a = \left( {2; - 3;1} \right)\) và \(\overrightarrow b = \left( { - 1;4; - 2} \right)\). Giá trị của biểu thức \(\overrightarrow a .\overrightarrow b \) bằng A. \( - 16.\) B. \( - 4.\) C. 4. D. 16. Câu 12: Trong không gian Oxyz, hình chiếu vuông góc của điểm \(A\left( {3;2; - 4} \right)\) lên mặt phẳng \(\left( {Oxy} \right)\) có tọa độ là A. \(\left( {0;2; - 4} \right).\) B. \(\left( {0;0; - 4} \right).\) C. \(\left( {3;0; - 4} \right).\) D. \(\left( {3;2;0} \right).\) Câu 13: Cho hàm số \(f\left( x \right)\)liên tục và không âm trên đoạn \(\left[ {a;b} \right]\), diện tích hình phẳng giới hạn bởi đồ thị hàm số \(f\left( x \right)\), các đường thẳng \(x = a,\,\,x = b\) và trục Ox là A. \( - \int\limits_a^b {f\left( x \right)dx} .\) B. \(\int\limits_a^b {f\left( x \right)dx} .\) C. \(\pi \int\limits_a^b {{{\left[ {f\left( x \right)} \right]}^2}dx} .\) D. \(\pi \int\limits_a^b {f\left( x \right)dx} .\) Câu 14: Họ nguyên hàm của hàm số \(y = {e^{2x}}\) là A. \(2{e^{2x}} + C.\) B. \(\frac{1}{2}{e^{2x}} + C.\) C. \({e^{2x}} + C.\) D. \(4{e^{2x - 1}} + C.\) Câu 15: Trong không gian Oxyz, cho điểm \(M\left( {1; - 2;5} \right)\). Khoảng cách từ M đến trục Oz bằng A. \(\sqrt 5 .\) B. 5. C. 1. D. 2. Câu 16: Họ nguyên hàm của hàm số \(f\left( x \right) = \frac{1}{{2x - 3}}\) là A. \(\frac{1}{2}\ln \left| {2x - 3} \right| + C.\) B. \(2\ln \left| {2x - 3} \right| + C.\) C. \(\frac{1}{3}\ln \left| {2x - 3} \right| + C.\) D. \(\ln \left| {2x - 3} \right| + C.\) Câu 17: \(\int\limits_0^1 {\left| {x - 2} \right|dx} \) bằng A. 2. B. \(\frac{3}{2}.\) C. \( - \frac{3}{2}.\) D. \(\frac{1}{2}.\) Câu 18: Trong không gian Oxyz, mặt phẳng \(\left( \alpha \right):x - 2y + z - 4 = 0\) đi qua điểm nào sau đây? A. \(N\left( {0;2;0} \right)\) B. \(M\left( {1;0;0} \right)\) C. \(P\left( {0;0; - 4} \right)\) D. \(Q\left( {1; - 1;1} \right)\) Câu 19: Gọi các số phức \({z_1};\,\,{z_2}\) là các nghiệm của phương trình \(3{z^2} - 2z + 12 = 0\). Giá trị biểu thức \(M = 2\left| {{z_1}} \right| - 3\left| {{z_2}} \right|\) bằng A. 2. B. \( - 4.\) C. \( - 2.\) D. \( - 12.\) Câu 20: Trong không gian Oxyz. Cho mặt phẳng \(\left( P \right):2x - y + 2z - 4 = 0\). Khoảng cách từ điểm \(M\left( {3;1; - 2} \right)\) đến mặt phẳng \(\left( P \right)\) bằng: A. \(\frac{1}{3}.\) B. 2. C. 3. D. 1. Câu 21: Cho biết \(\int\limits_0^{\frac{\pi }{2}} {\left( {4 - \sin x} \right)dx} = a\pi + b\), với \(a,\,\,b\) là các số nguyên. Giá trị biểu thức \(a + b\) bằng A. \( - 4.\) B. 6. C. 1. D. 3. Câu 22: Trong không gian Oxyz, mặt cầu \(\left( S \right):{x^2} + {y^2} + {\left( {z + 2} \right)^2} = 17\) cắt trục Oz tại hai điểm A, B. Độ dài đoạn AB bằng A. \(4\sqrt {13} \) B. \(2\sqrt {17} \) C. \(2\sqrt 3 \) D. \(\sqrt {17} \) Câu 23: Trong không gian Oxyz, mặt cầu \(\left( S \right):{x^2} + {y^2} + {z^2} - 2x + 4y - 6z - 11 = 0\) có bán kính bằng A. 11. B. \(\sqrt 3 \) C. 25. D. 5. Câu 24: Cho hàm số \(f\left( x \right)\) có đạo hàm liên tục trên đoạn \(\left[ {0;1} \right]\) và thỏa mãn \(\int\limits_0^1 {f'\left( x \right)dx = - 3} \). Giá trị biểu thức \(f\left( 0 \right) - f\left( 1 \right)\) bằng A. \( - 2.\) B. 1. C. 3. D. \( - 3.\) Câu 25: Họ nguyên hàm của hàm số \(f\left( x \right) = 2\sin x.\cos 2x\) là A. \( - \frac{1}{3}{\rm{cos}}3x + \cos x + C.\) B. \(\frac{1}{3}{\rm{cos}}3x + \cos x + C.\) C. \(\frac{1}{3}{\rm{cos}}3x - \cos x + C.\) D. \( - {\rm{cos}}3x + \cos x + C.\) Câu 26: Cho hàm số \(f\left( x \right)\) liên tục trên tập \(\mathbb{R}\) và thỏa mãn \(\int\limits_1^2 {f\left( x \right)dx = 3} ,\) \(\int\limits_0^2 {f\left( x \right)dx = - 5} \). Giá trị \(\int\limits_0^1 {f\left( x \right)dx} \) bằng A. 8. B. \( - 15\). C. \( - 8\). D. \( - 2.\) Câu 27: Cho số phức \(z = 2 - i + \frac{{ - 1 + i}}{{1 - 3i}}\). Giá trị của \(\left| z \right|\) bằng A. \(\sqrt 2 \) B. \(2\sqrt 3 \) C. 2 D. \(\sqrt {10} \) Câu 28: Trong không gian Oxyz, cho các vecto \(\overrightarrow a = \left( {5;3; - 2} \right)\) và \(\overrightarrow b = \left( {m; - 1;m + 3} \right)\). Có bao nhiêu giá trị nguyên dương của m để góc giữa hai vecto \(\overrightarrow a ;\,\,\overrightarrow b \) là góc tù? A. 2. B. 3. C. 1. D. 5. Câu 29: Cho hàm số \(f\left( x \right)\) liên tục trên \(\mathbb{R}\), một nguyên hàm của \(f\left( x \right)\) là \(F\left( x \right)\) thỏa mãn \(F\left( 1 \right) = - 3\) và \(F\left( 0 \right) = 1\). Giá trị \(\int\limits_0^1 {f\left( x \right)dx} \) bằng A. \( - 4.\) B. \( - 3.\) C. \( - 2.\) D. 4. Câu 30: Trong không gian Oxyz, mặt phẳng \(\left( P \right):3x + y - 4z - 12 = 0\) cắt trục Ox tại A, cắt trục Oz tại B. Chu vi tam giác OAB bằng: A. 6. B. 12. C. 36. D. 5. Câu 31: Trong không gian Oxyz, cho đường thẳng \(d:\left\{ \begin{array}{l}x = 4 - 2t\\y = - 3 + t\\z = 1 - t\end{array} \right.\), giao điểm của d với mặt phẳng \(\left( {Oxy} \right)\) có tọa độ là: A. \(\left( {4; - 3;0} \right)\). B. \(\left( {2; - 2;0} \right)\) C. \(\left( {0; - 1; - 1} \right)\) D. \(\left( { - 2;0; - 2} \right)\) Câu 32: Cho hai số phức \(z = 3 - 4i\) và \(z' = \left( {2 + m} \right) + mi\,\,\,\left( {m \in \mathbb{R}} \right)\) thỏa mãn \(\left| {z'} \right| = \left| {iz} \right|\). Tổng tất cả các giá trị của m bằng A. \( - 1.\) B. \(\frac{{\sqrt {46} }}{2}.\) C. 0. D. \( - 2.\) Câu 33: Hàm số \(f\left( x \right) = {e^{ - x}} + 2x - 5\) là nguyên hàm của hàm số nào sau đây? A. \(y = - {e^{ - x}} + \frac{1}{2}{x^2} - 5x + 1.\) B. \(y = {e^{ - x}} + {x^2} - 5x.\) C. \(y = - {e^{ - x}} + 2.\) D. \(y = - {e^{ - x}} + {x^2} - 5x + 3.\) Câu 34: Trong không gian Oxyz, cho mặt cầu \(\left( S \right):{\left( {x - 1} \right)^2} + {\left( {y - 2} \right)^2} + {\left( {z + 1} \right)^2} = 45\) và mặt phẳng \(\left( P \right):x + y - z - 13 = 0\). Mặt cầu \(\left( S \right)\) cắt mặt phẳng \(\left( P \right)\) theo giao tuyến là đường tròn có tâm \(I\left( {a;b;c} \right)\) thì giá trị của \(a + b + c\) bằng: A. 5. B. 2. C. \( - 11.\) D. 1. Câu 35: Trong không gian Oxyz, cho điểm \(A\left( {3;0;0} \right),\) \(B\left( {0; - 2;0} \right)\) và \(C\left( {0;0; - 4} \right)\). Mặt cầu ngoại tiếp tứ diện OABC có diện tích bằng A. \(116\pi .\) B. \(29\pi .\) C. \(16\pi \) D. \(\frac{{29\pi }}{4}\) Câu 36: Có bao nhiêu giá trị nguyên dương của a để \(\int\limits_0^a {\left( {2x - 3} \right) \le 4} \)? A. 6. B. 5. C. 3. D. 4. Câu 37: Cho số phức z thỏa mãn \(\frac{{\left( { - 1 + i} \right)z + 2}}{{1 - 2i}} = 2 + 3i\). Số phức liên hợp của z là \(\overline z = a + bi\) với \(a,\,\,b \in \mathbb{R}\). Giá trị của \(a + b\) bằng: A. \( - 1\). B. \( - 12.\) C. \( - 6\) D. 1. Câu 38: Cho hàm số \(f\left( x \right)\) liên tục trên đoạn \(\left[ {a;b} \right]\) và thỏa mãn \(\int\limits_a^0 {f\left( x \right)dx = m} \), \(\int\limits_0^b {f\left( x \right)dx = n} \). Diện tích hình phẳng trong hình vẽ bằng
A. \(m.n\) B. \(m - n\) C. \(m + n\) D. \(n - m\) Câu 39: Cho các số phức \({z_1} = 3 - 2i,\) \({z_2} = 1 + 4i\) và \({z_3} = - 1 + i\) có biểu diễn hình học trong mặt phẳng tọa độ Oxy lần lượt là các điểm \(A,B,C\). Diện tích tam giác ABC bằng: A. \(2\sqrt {17.} \) B. 12. C. \(4\sqrt {13} \) D. 9. Câu 40: Cho biết \(\int\limits_1^e {\frac{{\sqrt {\ln x + 3} }}{x}dx = \frac{a}{3} + b\sqrt 3 } \) với \(a,\,\,b\) là các số nguyên. Giá trị của biểu thức \(\frac{1}{{{2^b}}} + {\log _2}a\) bằng A. \( - 1.\) B. \(\frac{7}{2}.\) C. 8. D. 6. Câu 41: Trong không gian Oxyz, cho mặt phẳng \(\left( P \right)\) chứa điểm \(A\left( {3; - 1;2} \right)\) và đường thẳng \(d:\left\{ \begin{array}{l}x = t\\y = 1 + t\\z = 3 - 2t\end{array} \right.\). Mặt phẳng \(\left( P \right)\) có phương trình là: A. \(3x - 5y - z + 8 = 0\) B. \(2x + y - 2z - 6 = 0\) C. \(x + y + z - 4 = 0.\) D. \(x - 2y + z - 7 = 0\) Câu 42: Cho biết \(\int\limits_0^1 {\frac{{x - 1}}{{x + 2}}dx = a + b\ln \frac{3}{2}} \) với \(a,\,\,b\) là các số nguyên. Giá trị của biểu thức \(a - 2b\) bằng A. 6. B. 3. C. \( - 5.\) D. 7. Câu 43: Cho số phức z thỏa mãn \(\frac{{3 - 4i}}{z} = \frac{{\left( {2 + 3i} \right)\overline z }}{{{{\left| z \right|}^2}}} + 2 + i\), giá trị của \(\left| z \right|\) bằng A. \(\sqrt 5 \) B. \(\sqrt {10} \) C. 1 D. \(\sqrt 2 \) Câu 44: Cho biết \(\int\limits_0^1 {x\sqrt {{x^2} + 1} dx = \frac{{a\sqrt 2 - 1}}{b}} \) với \(a,\,\,b\) là các số tự nhiên. Giá trị của \({a^2} - {b^2}\) bằng A. \( - 5.\) B. 5. C. 2. D. 1. Câu 45: Cho hàm số \(f\left( x \right)\) có đạo hàm liên tục trên tập hợp \(\mathbb{R}\) thỏa mãn \(\int\limits_1^2 {f\left( {3x - 6} \right)dx = 3} \) và \(f\left( { - 3} \right) = 2\). Giá trị của \(\int\limits_{ - 3}^0 {xf'\left( x \right)dx} \) bằng: A. \( - 3\) B. 11 C. 6 D. 9 Câu 46: Trong không gian Oxyz, cho hai điểm \(A\left( {1; - 2;3} \right),\) \(B\left( {3;2; - 2} \right)\) và mặt phẳng \(\left( P \right):x + 2y - 4z - 7 = 0\). Đường thẳng AB cắt mặt phẳng \(\left( P \right)\) tại M. Giá trị của biểu thức \(\frac{{MA}}{{MB}}\) bằng A. \(\frac{5}{{21}}.\) B. 1. C. \(\frac{1}{3}.\) D. \(\frac{{11}}{4}.\) Câu 47: Gọi z là một nghiệm của phương trình \({z^2} - z + 1 = 0\). Giá trị của biểu thức \(M = {z^{2019}} + {z^{2018}} + \frac{1}{{{z^{2019}}}} + \frac{1}{{{z^{2018}}}} + 5\) bằng A. 5. B. 2. C. 7. D. \( - 1\) Câu 48: Có bao nhiêu số phức z thỏa mãn \(\left| {z - 2 + 3i} \right| = \left| {z + 1 - i} \right|\) và \({\left| z \right|^2} + 2\left( {z + \overline z } \right) = 5\)? A. 1. B. 0. C. 2. D. 4. Câu 49: Trong không gian Oxyz, cho mặt cầu \(\left( S \right):{\left( {x - 1} \right)^2} + {y^2} + {\left( {z + 2} \right)^2} = 4\) và điểm \(M\left( {3;1;2} \right)\). Điểm A di chuyển trên mặt cầu \(\left( S \right)\) thỏa mãn \(\overrightarrow {OA} .\overrightarrow {MA} = - 3\) thì A thuộc mặt phẳng nào trong các mặt phẳng sau? A. \(x + y + 6z - 2 = 0.\) B. \(3x + y + 2z - 3 = 0.\) C. \(5x + y - 2z - 4 = 0.\) D. \(2x - 4z - 1 = 0\) Câu 50: Cho hàm số \(f\left( x \right)\) liên tục trên \(\mathbb{R}\) \(f\left( {3x} \right) = f\left( x \right) - 2x,\,\,\,\forall x \in \mathbb{R}\) và \(\int\limits_0^1 {f\left( x \right)dx = 5} \). Giá trị \(\int\limits_1^3 {f\left( x \right)dx} \) bằng A. 4. B. 10. C. 7. D. 12. Lời giải chi tiết
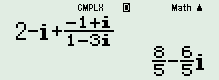
Câu 1 (NB) Phương pháp: Number \(z = a + bi\) has a virtual part is b . Cách giải: Number \(z = 5 - 2i\) has an virtual part is \( - 2\). Chọn D. Câu 2 (NB) Phương pháp: Cho hàm số \(f\left( x \right)\) liên tục trên đoạn \(\left[ {a;b} \right]\). Khi quay hình phẳng như hình vẽ bên quanh trục Ox ta được khối tròn xoay có thể phân tích là: \(V = \pi \int\limits_a^b {{{\left[ {f\left( x \right)} \ phải]}^2}dx} \) Cách giải: Cho hàm số \(f\left( x \right)\) liên tục trên đoạn \(\left[ {a;b} \right]\). Khi quay hình phẳng như hình vẽ bên quanh trục Ox ta được khối tròn xoay có thể phân tích là: \(V = \pi \int\limits_a^b {{{\left[ {f\left( x \right)} \ phải]}^2}dx} \) Chọn A. Câu 3 (NB) Phương pháp: Tìm nguyên hàm của hàm số lượng giác: \(\int {\frac{1}{{{\sin }^2}x}}dx = - \cot x + C} \). Cách giải: \(\int {\frac{1}{{{{\sin}^2}x}}dx = - \cot x + C} \) Chọn A. Câu 4 (NB) Phương pháp: Áp dụng các công thức tính nguyên hàm: \(\int {{x^n}dx} = \frac{{{x^{n + 1}}}}{{n + 1}} + C\) \(\left( {n \ne - 1} \right)\), \(\int {\frac{1}{x}dx} = \ln \left| x \right| + C\). Cách giải: \(\begin{array}{l}\int\limits_1^2 {\left( {2x + 1 + \frac{1}{x}} \right)} dx\\ = \left. {\left( {{x^2} + x + \ln \left| x \right|} \right)} \right|_1^2\\ = 4 + 2 + \ln 2 - \left( {1 + 1 + \ln 1} \right)\\ = 4 + \ln 2\end{array}\) Chọn C. Câu 5 (NB) Phương pháp: - Mặt cầu có tâm là \(I\left( {2; - 2;1} \right)\) và đi qua gốc tọa độ O thì có bán kính bằng \(R = OI\). - Sử dụng công thức tính độ dài đoạn thẳng \(OI = \sqrt {{{\left( {{x_I} - {x_O}} \right)}^2} + {{\left( {{y_I} - {y_O}} \right)}^2} + {{\left( {{z_I} - {z_O}} \right)}^2}} \). Cách giải: Vì mặt cầu tâm I đi qua gốc tọa độ O nên có bán kính \(R = IO = \sqrt {{2^2} + {{\left( { - 2} \right)}^2} + {1^2}} = 3.\) Chọn C. Câu 6 (NB) Phương pháp: Trung điểm đoạn AB có tọa độ là \(\left( {\frac{{{x_A} + {x_B}}}{2};\frac{{{y_A} + {y_B}}}{2};\frac{{{z_A} + {z_B}}}{2}} \right)\). Cách giải: Gọi I là trung điểm đoạn AB ta có: \(\left\{ \begin{array}{l}{x_I} = \frac{{1 + 5}}{2} = 3\\{y_I} = \frac{{2 - 4}}{2} = - 1\\{z_I} = \frac{{ - 3 + 1}}{2} = - 1\end{array} \right.\)\( \Rightarrow I\left( {3; - 1; - 1} \right).\) Chọn A. Câu 7 (NB) Phương pháp: Áp dụng các công thức tính nguyên hàm cơ bản: \(\int {{x^n}dx} = \frac{{{x^{n + 1}}}}{{n + 1}} + C\) \(\left( {n \ne - 1} \right)\). Cách giải: \(\int {{x^\pi }dx = \frac{{{x^{\pi + 1}}}}{{\pi + 1}} + C} .\) Chọn D. Câu 8 (TH) Phương pháp: - Điểm \(M\left( {a;b} \right)\) biểu diễn cho số phức \(z = a + bi\). - Số phức \(z = a + bi\) có môđun \(\left| z \right| = \sqrt {{a^2} + {b^2}} \). Cách giải: Ta có \(M\left( {3; - 4} \right)\) là điểm biểu diễn của số phức z nên \(z = 3 - 4i.\) Vậy \(\left| z \right| = \sqrt {{3^2} + {{\left( { - 4} \right)}^2}} = 5.\) Chọn B. Câu 9 (NB) Phương pháp: - Đường thẳng \(\left\{ \begin{array}{l}x = {x_0} + at\\y = {y_0} + bt\\z = {z_0} + bt\end{array} \right.\) có 1 VTCP là \(\overrightarrow u \left( {a;b;c} \right)\). - Mọi vectơ cùng phương với \(\overrightarrow u \) đều là 1 VTCP của đường thẳng trên. Cách giải: Đường thẳng \(d:\left\{ \begin{array}{l}x = 2 + t\\y = - 1 + 3t\\z = 3\end{array} \right.\) có vecto chỉ phương là \(\overrightarrow {{u_2}} = \left( {1;3;0} \right).\) Chọn C. Câu 10 (NB) Phương pháp: Sử dụng công thức \(z.\overline z = {\left| z \right|^2}\). Cách giải: \(z.\overline z = {\left| z \right|^2} = {3^2} + {2^2} = 13.\) Chọn C. Câu 11 (NB) Phương pháp: Cho hai vecto \(\overrightarrow a = \left( {{x_1};{y_1};{z_1}} \right)\) và \(\overrightarrow b = \left( {{x_2};{y_2};{z_2}} \right)\). Khi đó \(\overrightarrow a .\overrightarrow b = {x_1}{x_2} + {y_1}{y_2} + {z_1}{z_2}\). Cách giải: Ta có \(\overrightarrow a = \left( {2; - 3;1} \right);\) \(\overrightarrow b = \left( { - 1;4; - 2} \right).\) \( \Rightarrow \overrightarrow a .\overrightarrow b = 2.\left( { - 1} \right) + \left( { - 3} \right).4 + 1.\left( { - 2} \right) = - 16.\) Chọn A. Câu 12 (NB) Phương pháp: Trong không gian Oxyz, hình chiếu vuông góc của điểm \(A\left( {x;y;z} \right)\) lên mặt phẳng \(\left( {Oxy} \right)\) có tọa độ là \(\left( {x;y;0} \right)\). Cách giải: Hình chiếu vuông góc của điểm \(A\left( {3;2; - 4} \right)\) lên mặt phẳng \(\left( {Oxy} \right)\) có tọa độ là \(\left( {3;2;0} \right).\) Chọn D. Câu 13 (NB) Phương pháp: Cho hàm số \(f\left( x \right)\)liên tục \(\left[ {a;b} \right]\), diện tích hình phẳng giới hạn bởi đồ thị hàm số \(f\left( x \right)\), các đường thẳng \(x = a,\,\,x = b\) và trục Ox là \(S = \int\limits_a^b {\left| {f\left( x \right)} \right|dx} .\) Cách giải: Hình phẳng giới hạn bởi đồ thị hàm số \(f\left( x \right)\), các đường thẳng\(x = a,\,\,x = b\) và trục Ox có diện tích là \(S = \int\limits_a^b {\left| {f\left( x \right)} \right|dx} \). Mà \(f\left( x \right) \ge 0\) \(\forall x \in \left[ {a;b} \right]\), do đó \(S = \int\limits_a^b {f\left( x \right)dx} \). Chọn B. Câu 14 (NB) Phương pháp: Áp dụng công thức tính nguyên hàm mở rộng \(\int {{e^{ax + b}}dx = \frac{{{e^{ax + b}}}}{a} + C} .\) Cách giải: \(\int {{e^{2x}}dx = } \frac{1}{2}{e^{2x}} + C.\) Chọn B. Câu 15 (NB) Phương pháp: Khoảng cách từ điểm \(M\left( {a;b;c} \right)\) đến trục \(Oz\) là \(d\left( {M;Oz} \right) = \sqrt {{x^2} + {y^2}} \). Cách giải: Khoảng cách từ điểm \(M\left( {1; - 2;5} \right)\) đến trục \(Oz\) là \(d\left( {M;Oz} \right) = \sqrt {{1^2} + {{\left( { - 2} \right)}^2}} = \sqrt 5 \). Chọn A. Câu 16 (NB) Phương pháp: Áp dụng công thức tính nguyên hàm mở rộng: \(\int {\frac{1}{{ax + b}}dx = \frac{1}{a}\ln \left| {ax + b} \right|} + C.\) Cách giải: \(\int {\frac{1}{{2x - 3}}dx = \frac{1}{2}\ln \left| {2x - 3} \right|} + C.\) Chọn A. Câu 17 (TH) Phương pháp: - Phá dấu của trị tuyệt đối. - Áp dụng các công thức tính nguyên hàm cơ bản: \(\int {{x^n}dx} = \frac{{{x^{n + 1}}}}{{n + 1}} + C\) \(\left( {n \ne - 1} \right)\). Cách giải: Ta có \(x - 2 < 0\,\,\forall x \in \left[ {0;1} \right]\) \( \Rightarrow \int\limits_0^1 {\left| {x - 2} \right|dx} = \int\limits_0^1 {\left( {2 - x} \right)dx} \) \( = \left. {\left( {2x - \frac{{{x^2}}}{2}} \right)} \right|_0^1 = \frac{3}{2}.\) Chọn B. Câu 18 (NB) Phương pháp: Thay lần lượt tọa độ các điểm vào phương trình mặt phẳng. Cách giải: Ta thấy \(Q\left( {1; - 1;1} \right) \in \left( \alpha \right):x - 2y + z - 4 = 0\) vì \(1 - 2.\left( { - 1} \right) + 1 - 4 = 0\). Chọn D. Câu 19 (NB) Phương pháp: - Giải phương trình bậc hai tìm hai nghiệm \({z_1},\,\,{z_2}\). - Số phức \(z = a + bi\) có môđun \(\left| z \right| = \sqrt {{a^2} + {b^2}} \). Tính \(\left| {{z_1}} \right|,\,\,\left| {{z_2}} \right|\). - Thay vào tính giá trị biểu thức \(M\). Cách giải: Phương trình \(3{z^2} - 2z + 12 = 0\)\( \Leftrightarrow \left[ \begin{array}{l}{z_1} = \frac{1}{3} + \frac{{\sqrt {35} }}{3}i\\{z_2} = \frac{1}{3} - \frac{{\sqrt {35} }}{3}i\end{array} \right.\) \( \Rightarrow \left| {{z_1}} \right| = \left| {{z_2}} \right| = 2\). Vậy \(M = 2\left| {{z_1}} \right| - 3\left| {{z_2}} \right| = 2.2 - 3.2 = - 2.\) Chọn C. Câu 20 (NB) Phương pháp: Khoảng cách từ \(M\left( {{x_0};{y_0};{z_0}} \right)\) đến mặt phẳng \(\left( P \right):\,\,Ax + By + Cz + D = 0\) là \(d\left( {M;\left( P \right)} \right) = \frac{{\left| {A{x_0} + B{y_0} + C{z_0} + D} \right|}}{{\sqrt {{A^2} + {B^2} + {C^2}} }}\). Cách giải: Khoảng cách từ \(M\left( {3;1; - 2} \right)\) đến mặt phẳng \(\left( P \right):2x - y + 2z - 4 = 0\) là \(d = \frac{{\left| {2.3 - 1 + 2\left( { - 2} \right) - 4} \right|}}{{\sqrt {{2^2} + {1^2} + {2^2}} }} = 1.\) Chọn D. Câu 21 (TH) Phương pháp: - Áp dụng các công thức tính nguyên hàm cơ bản: \(\int {{x^n}dx} = \frac{{{x^{n + 1}}}}{{n + 1}} + C\) \(\left( {n \ne - 1} \right)\), \(\int {\sin xdx} = - \cos x + C\). - Đồng nhất hệ số tìm \(a,\,\,b\) và tính tổng \(a + b\). Cách giải: Ta có \(\begin{array}{l}\int\limits_0^{\frac{\pi }{2}} {\left( {4 - \sin x} \right)dx} \\ = \left. {\left( {4x + \cos x} \right)} \right|_0^{\frac{\pi }{2}}\\ = 2\pi + \cos \frac{\pi }{2} - \left( {0 + \cos 0} \right)\\ = 2\pi - 1\end{array}\) \( \Rightarrow a = 2,\,\,b = - 1.\) Vậy \(a + b = 2 + \left( { - 1} \right) = 1.\) Chọn C. Câu 22 (TH) Phương pháp: - Tìm giao điểm của mặt cầu với trục Oz bằng cách cho \(x = y = 0\). - Sử dụng công thức tính độ dài đoạn thẳng: \(AB\)\( = \sqrt {{{\left( {{x_B} - {x_A}} \right)}^2} + {{\left( {{y_B} - {y_A}} \right)}^2} + {{\left( {{z_B} - {z_A}} \right)}^2}} \) Cách giải: Cao độ của mặt cầu \(\left( S \right):{x^2} + {y^2} + {\left( {z + 2} \right)^2} = 17\) và trục Oz là nghiệm của phương trình: \({\left( {z + 2} \right)^2} = 17 \Rightarrow \left[ \begin{array}{l}z = \sqrt {17} - 2\\z = - \sqrt {17} - 2\end{array} \right.\). Suy ra giao điểm của mặt cầu \(\left( S \right)\) và trục \(Oz\) là: \(A\left( {0;0;\sqrt {17} - 2} \right)\) và \(B\left( {0;0; - \sqrt {17} - 2} \right)\). Vậy \(AB = \sqrt {{{\left( { - 2\sqrt {17} } \right)}^2}} = 2\sqrt {17} .\) Chọn B. Câu 23 (NB) Phương pháp: Mặt cầu \(\left( S \right):\)\({x^2} + {y^2} + {z^2} + 2ax + 2by + 2cz + d = 0\) có tâm \(I\left( {a;b;c} \right)\) và bán kính \(R = \sqrt {{a^2} + {b^2} + {c^2} - d} \) với \({a^2} + {b^2} + {c^2} - d > 0\). Cách giải: Mặt cầu \(\left( S \right):{x^2} + {y^2} + {z^2} - 2x + 4y - 6z - 11 = 0\) có bán kính \(R = \sqrt {1 + {{\left( { - 2} \right)}^2} + {3^2} + 11} = \sqrt {25} = 5.\) Chọn D. Câu 24 (TH) Phương pháp: Sử dụng công thức tính phân Newton – Leibniz: \(\int\limits_a^b {f'\left( x \right)dx} = f\left( b \right) - f\left( a \right)\). Cách giải: Ta có \(\int\limits_0^1 {f'\left( x \right)dx} = f\left( 1 \right) - f\left( 0 \right) = - 3.\) Vậy \(f\left( 0 \right) - f\left( 1 \right) = 3.\) Chọn C. Câu 25 (TH) Phương pháp: - Áp dụng công thức biến đổi tích thành tổng: \(\sin a\cos b = \frac{1}{2}\left[ {\sin \left( {a + b} \right) + \sin \left( {a - b} \right)} \right]\). - Áp dụng các công thức tính nguyên hàm: \(\int {\sin \left( {ax + b} \right)dx} = - \frac{1}{a}\cos \left( {ax + b} \right) + C\). Cách giải: Ta có \(f\left( x \right) = 2\sin x\cos 2x \) \(= \sin 3x + \sin \left( { - x} \right) = \sin 3x - \sin x\). Khi đó ta có \(\int {f\left( x \right)dx} = \int {\left( {\sin 3x - \sin x} \right)dx} \)\( = - \frac{1}{3}\cos 3x + \cos x + C\). Chọn A. Câu 26 (NB) Phương pháp: Áp dụng tính chất của tích phân: \(\int\limits_a^b {f\left( x \right)dx} = \int\limits_a^c {f\left( x \right)dx} + \int\limits_c^b {f\left( x \right)dx} ,\) \(\int\limits_a^b {f\left( x \right)dx} = - \int\limits_b^a {f\left( x \right)dx} .\) Cách giải: Ta có \(\int\limits_1^2 {f\left( x \right)dx} = - \int\limits_2^1 {f\left( x \right)dx} \). Vậy \(\int\limits_0^1 {f\left( x \right)dx} = \int\limits_0^2 {f\left( x \right)dx} + \int\limits_2^1 {f\left( x \right)dx} \)\( = - 5 - 3 = - 8\) Chọn C. Câu 27 (TH) Phương pháp: - Tính số phức z bằng MTCT. - Số phức \(z = a + bi\) có môđun \(\left| z \right| = \sqrt {{a^2} + {b^2}} \). Cách giải: Sử dụng MTCT ta có \(z = 2 - i + \frac{{ - 1 + i}}{{1 - 3i}} = \frac{8}{5} - \frac{6}{5}i.\)
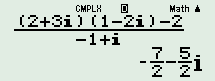
Vậy \(\left| z \right| = \sqrt {{{\left( {\frac{8}{5}} \right)}^2} + {{\left( { - \frac{6}{5}} \right)}^2}} = 2.\) Chọn C. Câu 28 (TH) Phương pháp: - Áp dụng công thức tính góc giữa hai vecto: \(\cos \left( {\overrightarrow a ;\overrightarrow b } \right) = \frac{{\overrightarrow a .\overrightarrow b }}{{\left| {\overrightarrow a } \right|.\left| {\overrightarrow b } \right|}}\). - Để góc giữa hai vectơ \(\overrightarrow a ;\,\,\overrightarrow b \) là góc tù thì \(\cos \left( {\overrightarrow a ;\overrightarrow b } \right) > 0\). Cách giải: Ta có \(\overrightarrow a = \left( {5;3; - 2} \right)\) và \(\overrightarrow b = \left( {m; - 1;m + 3} \right)\). \(\begin{array}{l}\cos \left( {\overrightarrow a ;\overrightarrow b } \right)\\ = \frac{{5m - 3 - 2m - 6}}{{\sqrt {38\left( {{m^2} + 1 + {{\left( {m + 3} \right)}^2}} \right)} }}\\ = \frac{{3m - 9}}{{\sqrt {38\left( {{m^2} + 1 + {{\left( {m + 3} \right)}^2}} \right)} }}\end{array}\) Mà góc giữa hai vecto \(\overrightarrow a ;\overrightarrow b \) là góc tù nên \(\cos \left( {\overrightarrow a ;\overrightarrow b } \right) < 0\). \( \Rightarrow 3m - 9 < 0 \Leftrightarrow m < 3.\) Mà \(m \in {\mathbb{Z}^ + }\)\( \Rightarrow m \in \left\{ {1;2} \right\}\). Vậy có hai giá trị của \(m\) thỏa mãn yêu cầu bài toán. Chọn A. Câu 29 (TH) Phương pháp: Sử dụng công thức tích phân Newton – Leibniz: Cho hàm số \(f\left( x \right)\) liên tục trên \(\mathbb{R}\), một nguyên hàm của \(f\left( x \right)\) là \(F\left( x \right)\). Khi đó ta có: \(\int\limits_a^b {f\left( x \right)dx} = F\left( b \right) - F\left( a \right)\). Cách giải: Ta có: \(\int\limits_0^1 {f\left( x \right)dx} = F\left( 1 \right) - F\left( 0 \right)\) \( = - 3 - 1 = - 4\) Chọn A. Câu 30 (VD) Phương pháp: - Tìm tọa độ điểm A, B. - Tính độ dài các cạnh \(OA,\,\,OB,\,\,OC\). Sử dụng công thức tính độ dài đoạn thẳng \(AB \)\(= \sqrt {{{\left( {{x_B} - {x_A}} \right)}^2} + {{\left( {{y_B} - {y_A}} \right)}^2} + {{\left( {{z_B} - {z_A}} \right)}^2}} \). - Tính chu vi tam giác OAB bằng \({P_{\Delta OAB}} = A + OB + AB\). Cách giải: Cho \(y = z = 0\) ta có \(3x - 12 = 0 \Leftrightarrow x = 4\). Suy ra mặt phẳng \(\left( P \right)\) cắt trục \(Ox\) tại \(A\left( {4;0;0} \right)\). Cho \(x = y = 0\) ta có \( - 4z - 12 = 0 \Leftrightarrow z = - 3\). Suy ra mặt phẳng \(\left( P \right)\) cắt trục \(Oz\) tại \(B\left( {0;0; - 3} \right)\). Ta có: \(OA = 4,\,\,OB = 3\) và \(AB = \sqrt {{{\left( { - 4} \right)}^2} + {0^2} + {{\left( { - 3} \right)}^2}} = 5\). Vậy chu vi tam giác OAB là \(4 + 3 + 5 = 12.\) Chọn B. Câu 31 (TH) Phương pháp: - Tìm giao điểm của d với mặt phẳng \(\left( {Oxy} \right)\) tức \(z = 0\). - Cho \(z = 0\) tìm \(t\), từ đó tìm được \(x,\,\,y\) và suy ra tọa độ giao điểm. Cách giải: Cho \(z = 0\)\( \Rightarrow 1 - t = 0 \Leftrightarrow t = 1\) Khi đó ta có \(\left\{ \begin{array}{l}x = 4 - 2t = 4 - 2.1 = 2\\y = - 3 + t = - 3 + 1 = - 2\end{array} \right.\) Vậy giao điểm của d với mặt phẳng \(\left( {Oxy} \right)\) có tọa độ là \(\left( {2; - 2;0} \right)\). Chọn B. Câu 32 (VD) Phương pháp: - Số phức \(z = a + bi\) có môđun \(\left| z \right| = \sqrt {{a^2} + {b^2}} \). - Lập phương trình bậc hai ẩn \(m\), áp dụng định lí Vi-ét: \({m_1} + {m_2} = \frac{{ - b}}{a}\). Cách giải: Ta có \(z = 3 - 4i\)\( \Rightarrow iz = i\left( {3 - 4i} \right) = 4 + 3i.\) Theo bài ra ta có: \(\begin{array}{l}\,\,\,\,\,\,\,\left| {z'} \right| = \left| {iz} \right|\\ \Leftrightarrow \sqrt {{{\left( {m + 2} \right)}^2} + {m^2}} = \sqrt {{4^2} + {3^2}} \\ \Leftrightarrow {\left( {m + 2} \right)^2} + {m^2} = 25\\ \Leftrightarrow 2{m^2} + 4m - 21 = 0\end{array}\) Áp dụng định lý viet ta có tổng các giá trị của m là \(\frac{{ - 4}}{2} = - 2.\) Chọn D. Câu 33 (TH) Phương pháp: Hàm số \(F\left( x \right)\) là 1 nguyên hàm của hàm số \(f\left( x \right)\) thì \(F'\left( x \right) = f\left( x \right)\). Cách giải: Ta có \(f\left( x \right) = {e^{ - x}} + 2x - 5\)\( \Rightarrow f'\left( x \right) = - {e^{ - x}} + 2\) Vậy \(f\left( x \right) = {e^{ - x}} + 2x - 5\) là một nguyên hàm của hàm số \( - {e^{ - x}} + 2\). Chọn C. Chú ý: Phân biệt với câu hỏi tìm nguyên hàm của hàm số \(f\left( x \right) = {e^{ - x}} + 2x - 5\). Câu 34 (VD) Phương pháp: - Mặt cầu \(\left( S \right)\) cắt mặt phẳng \(\left( P \right)\) theo giao tuyến là đường tròn có tâm \(I\) thì \(I\) chính là hình chiếu của tâm mặt cầu \(\left( S \right)\) lên mặt phẳng \(\left( P \right)\). - Xác định tâm \(A\) của mặt cầu \(\left( S \right)\). - Viết phương trình đường thẳng \(AI\) đi qua \(A\) và vuông góc với \(mp\left( P \right)\). - Tìm \(I\) là giao điểm của \(AI\) và \(\left( P \right)\). Cách giải: Ta có mặt cầu \(\left( S \right):{\left( {x - 1} \right)^2} + {\left( {y - 2} \right)^2} + {\left( {z + 1} \right)^2} = 45\) có tâm là \(A\left( {1;2; - 1} \right).\) Vì mặt cầu \(\left( S \right)\) cắt mặt phẳng \(\left( P \right)\) theo giao tuyến là đường tròn có tâm \(I\) thì \(I\) chính là hình chiếu của tâm mặt cầu \(\left( S \right)\) lên mặt phẳng \(\left( P \right)\). Do đó \(AI\) là đường thẳng đi qua \(A\) và vuông góc với \(mp\left( P \right)\). Ta có \({\overrightarrow u _{IA}} = \overrightarrow {{n_P}} = \left( {1;1; - 1} \right)\). Suy ra phương trinh đường thẳng \(AI:\,\,\left\{ \begin{array}{l}x = 1 + t\\y = 2 + t\\z = - 1 - t\end{array} \right.\). Vì \(I \in AI\) nên gọi \(I\left( {1 + t;2 + t; - 1 - t} \right).\) Mặt khác \(I \in \left( P \right)\), nên ta có: \(1 + t + 2 + t + 1 + t - 13 = 0\) \( \Leftrightarrow 3t - 9 = 0 \Leftrightarrow t = 3.\) \( \Rightarrow I\left( {4;5; - 4} \right) \Rightarrow a = 4,\,\,b = 5,\,\,c = - 4.\) Vậy \(a + b + c = 4 + 5 + \left( { - 4} \right) = 5.\) Chọn A. Câu 35 (VD) Phương pháp: - Gọi \(I\left( {a;b;c} \right)\) là tâm mặt cầu ngoại tiếp tứ diện \(OABC\) \( \Rightarrow IO = IA = IB = IC\). - Giải hệ phương trình \(\left\{ \begin{array}{l}I{O^2} = I{A^2}\\I{O^2} = I{B^2}\\I{O^2} = I{C^2}\end{array} \right.\) tìm tọa độ điểm \(I\). - Tính bán kính mặt cầu \(R = OI\). - Diện tích mặt cầu bán kính \(R\) là \(S = 4\pi {R^2}\). Cách giải: Gọi \(I\left( {a;b;c} \right)\) là tâm mặt cầu ngoại tiếp tứ diện \(OABC\) \( \Rightarrow IO = IA = IB = IC\)\( \Rightarrow I{O^2} = I{A^2} = I{B^2} = I{C^2}\). Khi đó ta có hệ phương trình: \(\left\{ \begin{array}{l}{x^2} + {y^2} + {z^2} = {\left( {x - 3} \right)^2} + {y^2} + {z^2}\\{x^2} + {y^2} + {z^2} = {x^2} + {\left( {y + 2} \right)^2} + {z^2}\\{x^2} + {y^2} + {z^2} = {x^2} + {y^2} + {\left( {z + 4} \right)^2}\end{array} \right.\) \( \Leftrightarrow \left\{ \begin{array}{l}{x^2} = {\left( {x - 3} \right)^2}\\{y^2} = {\left( {y + 2} \right)^2}\\{z^2} = {\left( {z + 4} \right)^2}\end{array} \right.\) \( \Leftrightarrow \left\{ \begin{array}{l} - 6x + 9 = 0\\4y + 4 = 0\\8z + 16 = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = \frac{3}{2}\\y = - 1\\z = - 2\end{array} \right.\) \( \Rightarrow I\left( {\frac{3}{2}; - 1;2} \right)\). Suy ra bán kính mặt cầu ngoại tiếp tứ diện \(OABC\) là \(R = IO = \sqrt {\frac{9}{4} + 1 + 4} = \sqrt {\frac{{29}}{4}} \). Váy diện tích cầu ngoại tiếp tứ diện \(OABC\) là \(S = 4\pi {R^2} = 4\pi .\frac{{29}}{4} = 29\pi .\) Chọn B. Câu 36 (VD) Phương pháp: - Áp dụng các công thức tính nguyên hàm cơ bản: \(\int {{x^n}dx} = \frac{{{x^{n + 1}}}}{{n + 1}} + C\) \(\left( {n \ne - 1} \right)\). - Giải bất phương trình tìm \(a\) và suy ra các giá trị của \(a\) thỏa mãn. Cách giải: Ta có \(\int\limits_0^a {\left( {2x - 3} \right)dx} = \left. {\left( {{x^2} - 3x} \right)} \right|_0^a = {a^2} - 3a.\) Theo bài ra ta có: \(\int\limits_0^a {\left( {2x - 3} \right)dx} \le 4\)\( \Rightarrow {a^2} - 3a \le 4 \Leftrightarrow - 1 \le a \le 4.\) Mà \(a \in {\mathbb{Z}^ + } \Rightarrow a \in \left\{ { - 1;0;1;2;3;4} \right\}.\) Vậy có 6 giá trị của \(a\) thỏa mãn yêu cầu bài toán. Chọn A. Câu 37 (VD) Phương pháp: - Tìm số phức z bằng MTCT rồi suy ra \(\overline z \): Số phức \(z = a + bi\) có số phức liên hợp \(\overline z = a - bi\). - Xác định các hệ số \(a,\,\,b\) và tính tổng \(a + b\). Cách giải: Ta có \(\frac{{\left( { - 1 + i} \right)z + 2}}{{1 - 2i}} = 2 + 3i\) \( \Rightarrow z = \frac{{\left( {2 + 3i} \right)\left( {1 - 2i} \right) - 2}}{{ - 1 + i}}\) \( = - \frac{7}{2} - \frac{5}{2}i\)
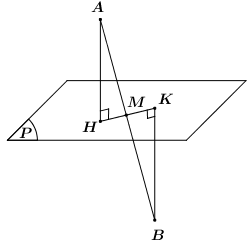
\(\begin{array}{l} \Rightarrow \overline z = - \frac{7}{2} + \frac{5}{2}i\\ \Rightarrow a = - \frac{7}{2};\,\,b = \frac{5}{2}\end{array}\) Vậy \(a + b = - \frac{7}{2} + \frac{5}{2} = - 1.\) Chọn A. Câu 38 (VD) Phương pháp: Cho hàm số \(f\left( x \right)\)liên tục \(\left[ {a;b} \right]\), diện tích hình phẳng giới hạn bởi đồ thị hàm số \(f\left( x \right)\), các đường thẳng \(x = a,\,\,x = b\) và trục Ox là \(S = \int\limits_a^b {\left| {f\left( x \right)} \right|dx} .\) Cách giải: Gọi \({S_1}\) là diện tích hình phẳng giới hạn bởi đồ thị hàm số \(y = f\left( x \right)\), trục hoành, đường thẳng \(x = a,\,\,x = 0\,\,\left( {a < 0} \right)\), ta có \({S_1} = \int\limits_a^0 {\left| {f\left( x \right)} \right|dx} = \int\limits_a^0 {f\left( x \right)dx} = m\). Gọi \({S_2}\) là diện tích hình phẳng giới hạn bởi đồ thị hàm số \(y = f\left( x \right)\), trục hoành, đường thẳng \(x = 0,\,\,x = b\,\,\left( {b > 0} \right)\), ta có \({S_2} = \int\limits_0^b {\left| {f\left( x \right)} \right|dx} = - \int\limits_0^b {f\left( x \right)dx} = - n\). Vậy diện tích cần tính là \(S = {S_1} + {S_2} = m - n.\) Chọn B. Câu 39 (VD) Phương pháp: - Suy ra tọa độ của A,B,C : Số phức \(z = a + bi\) được biểu diễn bởi điểm \(M\left( {a;b} \right)\). - Tính độ dài các đoạn thẳng \(AB,\,\,AC,\,\,BC\). Sử dụng công thức tính độ dài đoạn thẳng \(AB\)\( = \sqrt {{{\left( {{x_B} - {x_A}} \right)}^2} + {{\left( {{y_B} - {y_A}} \right)}^2} + {{\left( {{z_B} - {z_A}} \right)}^2}} \). - Sử dụng công thức Herong để tính diện tích tam giác: \({S_{\Delta ABC}} = \sqrt {p\left( {p - AB} \right)\left( {p - AC} \right)\left( {p - BC} \right)} \) với \(p\) là nửa chu vi tam giác \(ABC\). Cách giải: Ta có \({z_1} = 3 - 2i,\) \({z_2} = 1 + 4i\) và \({z_3} = - 1 + i\) có biểu diễn hình học trong mặt phẳng tọa độ Oxy lần lượt là các điểm \(A,B,C\) nên \(A\left( {3; - 2} \right);\,\,B\left( {1;4} \right);\,\,C\left( { - 1;1} \right).\) Khi đó ta có: \( \Rightarrow \left\{ \begin{array}{l}AB = \sqrt {{{\left( { - 2} \right)}^2} + {6^2}} = 2\sqrt {10} \\AC = \sqrt {{{\left( { - 4} \right)}^2} + {3^2}} = 5\\BC = \sqrt {{{\left( { - 2} \right)}^2} + {{\left( { - 3} \right)}^2}} = \sqrt {13} \end{array} \right..\) Gọi \(p\) là nửa chu vi tam giác \(ABC\) ta có: \(p = \frac{{2\sqrt {10} + 5 + \sqrt {13} }}{2}.\) Diện tích tam giác \(ABC\) là: \({S_{\Delta ABC}} \)\(= \sqrt {p\left( {p - AB} \right)\left( {p - AC} \right)\left( {p - BC} \right)} \) \(= 9.\) Chọn D. Câu 40 (VD) Phương pháp: - Sử dụng phương pháp đổi biến số, đặt \(t = \sqrt {\ln x + 3} \). - Tính tích phân sau khi đổi biến, đồng nhất hệ số tìm \(a,\,\,b\). Cách giải: Gọi \(I = \int\limits_1^e {\frac{{\sqrt {\ln x + 3} }}{x}dx} \). Đặt \(t = \sqrt {\ln x + 3} \)\( \Rightarrow {t^2} = \ln x + 3\) \( \Rightarrow 2tdt = \frac{{dx}}{x}\) . Đổi cận: \(\left\{ \begin{array}{l}x = 1 \Rightarrow t = \sqrt 3 \\x = e \Rightarrow t = 2\end{array} \right.\). Khi đó ta có: \(I = 2\int\limits_{\sqrt 3 }^2 {{t^2}dt} = \left. {\frac{{2{t^3}}}{3}} \right|_{\sqrt 3 }^2 = \frac{{16}}{3} - 2\sqrt 3 \). \( \Rightarrow a = 16,\,\,b = - 2.\) Vậy \(\frac{1}{{{2^b}}} + {\log _2}a = \frac{1}{{{2^{ - 2}}}} + {\log _2}16\)\( = 4 + 4 = 8\) Chọn C. Câu 41 (VD) Phương pháp: - Lấy điểm \(B\) bất kì thuộc đường thẳng \(d\). - \(\left\{ \begin{array}{l}AB \subset \left( P \right)\\d \subset \left( P \right)\end{array} \right. \Rightarrow \left\{ \begin{array}{l}\overrightarrow {AB} .\overrightarrow {{n_P}} = 0\\\overrightarrow {{u_d}} .\overrightarrow {{n_P}} = 0\end{array} \right.\)\( \Rightarrow \overrightarrow {{n_P}} = \left[ {\overrightarrow {AB} ;\overrightarrow {{u_d}} } \right]\) với \(\overrightarrow {{u_d}} \) là 1 VTCP của đường thẳng \(d\), \(\overrightarrow {{n_P}} \) là 1 VTPT của mặt phẳng \(\left( P \right)\). - Viết phương trình mặt phẳng đi qua \(A\left( {{x_0};{y_0};{z_0}} \right)\) và có 1 VTPT là \(\overrightarrow n \left( {A;B;C} \right)\) là: \(A\left( {x - {x_0}} \right) + \left( {y - {y_0}} \right) + C\left( {z - {z_0}} \right) = 0\). Cách giải: Ta có \(B\left( {0;1;3} \right) \in d\). Mà \(d \subset \left( P \right)\)\( \Rightarrow B\left( {0;1;3} \right) \in \left( P \right).\) \( \Rightarrow \overrightarrow {AB} = \left( { - 3;2;1} \right)\) Đường thẳng d có 1 vecto chỉ phương là \(\overrightarrow u = \left( {1;1; - 2} \right)\) Ta có: \(\left[ {\overrightarrow {AB} ;\overrightarrow {{u_d}} } \right] = \left( { - 5; - 5; - 5} \right)\parallel \left( {1;1;1} \right)\). Gọi \(\overrightarrow {{n_P}} \) là 1 VTPT của mặt phẳng \(\left( P \right)\). Vì \(\left\{ \begin{array}{l}AB \subset \left( P \right)\\d \subset \left( P \right)\end{array} \right. \Rightarrow \left\{ \begin{array}{l}\overrightarrow {AB} .\overrightarrow {{n_P}} = 0\\\overrightarrow {{u_d}} .\overrightarrow {{n_P}} = 0\end{array} \right.\) \( \Rightarrow \overrightarrow {{n_P}} \) cùng phương với \(\left[ {\overrightarrow {AB} ;\overrightarrow {{u_d}} } \right]\). Do đó \(\left( P \right)\) có 1 VTPT là \(\overrightarrow {{n_P}} = \left( {1;1;1} \right)\). Vậy phương trình mặt phẳng \(\left( P \right)\) là: \(x - 3 + y + 1 + z - 2 = 0\)\( \Leftrightarrow x + y + z - 4 = 0\) Chọn C. Câu 42 (VD) Phương pháp: - Bậc tử = bậc mẫu => Chia tử cho mẫu. - Áp dụng các công thức tính nguyên hàm cơ bản: \(\int {{x^n}dx} = \frac{{{x^{n + 1}}}}{{n + 1}} + C\) \(\left( {n \ne - 1} \right)\), \(\int {\frac{1}{{ax + b}}dx = \frac{1}{a}\ln \left| {ax + b} \right|} + C.\) - Đồng nhất hệ số tìm \(a,\,\,b\) và tính \(a - 2b\). Cách giải: Ta có \(\frac{{x - 1}}{{x + 2}} = \frac{{x + 2 - 3}}{{x + 2}}\)\( = 1 - \frac{3}{{x + 2}}\) . \(\begin{array}{l} \Rightarrow \int\limits_0^1 {\frac{{x - 1}}{{x + 2}}dx} \\ = \int\limits_0^1 {\left( {1 - \frac{3}{{x + 2}}} \right)dx} \\ = \left. {\left( {x - 3\ln \left| {x + 2} \right|} \right)} \right|_0^1\\ = 1 - 3\ln 3 - \left( {0 - 3\ln 2} \right)\\ = 1 - 3\ln \frac{3}{2}\end{array}\) \( \Rightarrow a = 1;\,\,b = - 3.\) Vậy \(a - 2b = 1 - 2.\left( { - 3} \right) = 7.\) Chọn D. Câu 43 (VD) Phương pháp: - Áp dụng công thức \(z.\overline z = {\left| z \right|^2}\). - Quy đồng mẫu tìm số phức \(z\). - Số phức \(z = a + bi\) có môđun \(\left| z \right| = \sqrt {{a^2} + {b^2}} \). Cách giải: Ta có \(\begin{array}{l}\frac{{3 - 4i}}{z} = \frac{{\left( {2 + 3i} \right)\overline z }}{{{{\left| z \right|}^2}}} + 2 + i\\ \Leftrightarrow \frac{{3 - 4i}}{z} = \frac{{\left( {2 + 3i} \right)\overline z }}{{z.\overline z }} + 2 + i\\ \Leftrightarrow \frac{{3 - 4i}}{z} = \frac{{2 + 3i}}{z} + 2 + i\\ \Leftrightarrow 3 - 4i = 2 + 3i + \left( {2 + i} \right).z\\ \Leftrightarrow \left( {2 + i} \right).z = 1 - 7i\\ \Leftrightarrow z = \frac{{1 - 7i}}{{2 + i}} = - 1 - 3i\end{array}\) Vậy \(\left| z \right| = \sqrt {{{\left( { - 1} \right)}^2} + {{\left( { - 3} \right)}^2}} = \sqrt {10} .\) Chọn B. Câu 44 (VD) Phương pháp: - Sử dụng phương pháp đổi biến số, đặt \(t = \sqrt {{x^2} + 1} \). - Tích tích phân sau khi đổi biến. - Đồng nhất hệ số tìm \(a,\,\,b\) và tính \({a^2} - {b^2}\). Cách giải: Đặt \(t = \sqrt {{x^2} + 1} \Rightarrow {t^2} = {x^2} + 1 \Rightarrow tdt = xdx\). Đổi cận: \(\left\{ \begin{array}{l}x = 0 \Rightarrow t = 1\\x = 1 \Rightarrow t = \sqrt 2 \end{array} \right.\). Khi đó ta có: \(\begin{array}{l}\int\limits_0^1 {x\sqrt {{x^2} + 1} dx} = \int\limits_1^{\sqrt 2 } {{t^2}dt} \\ = \left. {\frac{{{t^3}}}{3}} \right|_1^{\sqrt 2 } = \frac{{2\sqrt 2 }}{3} - \frac{1}{3}\\ = \frac{{2\sqrt 2 - 1}}{3}\end{array}\). \( \Rightarrow a = 2,\,\,b = 3\). Vậy \({a^2} - {b^2} = {2^2} - {3^2} = - 5.\) Chọn A. Câu 45 (VD) Phương pháp: - Áp dụng tích phân từng phần: \(\int\limits_a^b {udv} = \left. {uv} \right|_a^b - \int\limits_a^b {vdu} \). - Sử dụng phương pháp đổi biến để tính \(\int\limits_{ - 3}^0 {f\left( x \right)dx} .\) Cách giải: Ta gọi \(I = \int\limits_{ - 3}^0 {xf'\left( x \right)dx} \). Đặt \(\left\{ \begin{array}{l}u = x\\dv = f'\left( x \right)dx\end{array} \right. \Rightarrow \left\{ \begin{array}{l}du = dx\\v = f\left( x \right)\end{array} \right.\), khi đó ta có: \(\begin{array}{l}I = \left. {xf\left( x \right)} \right|_{ - 3}^0 - \int\limits_{ - 3}^0 {f\left( x \right)dx} \\I = 3f\left( { - 3} \right) - \int\limits_{ - 3}^0 {f\left( x \right)dx} \\I = 6 - \int\limits_{ - 3}^0 {f\left( x \right)dx} \end{array}\) Xét tích phân \(\int\limits_1^2 {f\left( {3x - 6} \right)dx = 3} \). Đặt \(t = 3x - 6 \Rightarrow dt = 3dx\). Đổi cận: \(\left\{ \begin{array}{l}x = 1 \Rightarrow t = - 3\\x = 2 \Rightarrow t = 0\end{array} \right.\). Khi đó ta có: \(\int\limits_1^2 {f\left( {3x - 6} \right)dx} = \frac{1}{3}\int\limits_{ - 3}^0 {f\left( t \right)dt} \)\( = \frac{1}{3}\int\limits_{ - 3}^0 {f\left( x \right)dx} = 3\) \( \Leftrightarrow \int\limits_{ - 3}^0 {f\left( x \right)dx} = 9.\) Vậy \(I = 6 - 9 = - 3.\) Chọn A. Câu 46 (VD) Phương pháp: - Xác định vị trí của A,B so với mặt phẳng \(\left( P \right)\). - Gọi \(H,\,\,K\) lần lượt là hình chiếu của \(A,\,\,B\) lên \(\left( P \right)\), sử dụng định lí Ta-lét chứng minh \(\frac{{MA}}{{MB}} = \frac{{AH}}{{BK}} = \frac{{d\left( {A;\left( P \right)} \right)}}{{d\left( {B;\left( P \right)} \right)}}\). - Khoảng cách từ \(M\left( {{x_0};{y_0};{z_0}} \right)\) đến mặt phẳng \(\left( P \right):\,\,Ax + By + Cz + D = 0\) là \(d\left( {M;\left( P \right)} \right) = \frac{{\left| {A{x_0} + B{y_0} + C{z_0} + D} \right|}}{{\sqrt {{A^2} + {B^2} + {C^2}} }}\). Cách giải:
Ta có \(\left\{ \begin{array}{l}{P_A} = 1 + 2.\left( { - 2} \right) - 4.3 - 7 = - 22\\{P_B} = 3 + 2.2 - 4.\left( { - 2} \right) - 7 = 8\end{array} \right.\) \( \Rightarrow {P_A}.{P_B} < 0 \Rightarrow A,\,\,B\) nằm khác phía so với mặt phẳng \(\left( P \right)\). Gọi \(H,\,\,K\) lần lượt là hình chiếu của \(A,\,\,B\) lên \(\left( P \right)\), ta có \(\left\{ \begin{array}{l}AH \bot \left( P \right)\\BK \bot \left( P \right)\end{array} \right. \Rightarrow AH\parallel BK\). Áp dụng định lí Ta-lét ta có: \(\frac{{MA}}{{MB}} = \frac{{AH}}{{BK}} = \frac{{d\left( {A;\left( P \right)} \right)}}{{d\left( {B;\left( P \right)} \right)}}\). Mà \(\begin{array}{l}d\left( {A;\left( P \right)} \right) = \frac{{\left| {1 + 2.\left( { - 2} \right) - 4.3 - 7} \right|}}{{\sqrt {{1^2} + {2^2} + {{\left( { - 4} \right)}^2}} }} = \frac{{22}}{{\sqrt {21} }}\\d\left( {B;\left( P \right)} \right) = \frac{{\left| {3 + 2.2 - 4.\left( { - 2} \right) - 7} \right|}}{{\sqrt {{1^2} + {2^2} + {{\left( { - 4} \right)}^2}} }} = \frac{8}{{\sqrt {21} }}\end{array}\) Vậy \(\frac{{MA}}{{MB}} = \frac{{d\left( {A;\left( P \right)} \right)}}{{d\left( {B;\left( P \right)} \right)}} = \frac{{22}}{8} = \frac{{11}}{4}.\) Chọn D. Câu 47 (VD) Phương pháp: - Giải phương trình bậc hai tìm một nghiệm \(z\). - Tính \({z^3}\), từ đó phân tích \({z^{2019}},\,\,{z^{2018}}\) theo \({z^3}\) và tính giá trị biểu thức \(M\). Cách giải: Ta có \({z^2} - z + 1 = 0 \Leftrightarrow \left[ \begin{array}{l}z = \frac{1}{2} + \frac{{\sqrt 3 }}{2}i\\z = \frac{1}{2} - \frac{{\sqrt 3 }}{2}i\end{array} \right.\). Chọn 1 nghiệm của phương trình trên là \(z = \frac{1}{2} + \frac{{\sqrt 3 }}{2}i\), ta có \({z^3} = - 1\).
Ta có: \(\begin{array}{l}{z^{2019}} = {\left( {{z^3}} \right)^{673}} = {\left( { - 1} \right)^{673}} = - 1\\{z^{2018}} = {\left( {{z^3}} \right)^{672}}.{z^2}\\ = {\left( { - 1} \right)^{672}}.{\left( {\frac{1}{2} + \frac{{\sqrt 3 }}{2}i} \right)^2}\\ = - \frac{1}{2} + \frac{{\sqrt 3 }}{2}i\end{array}\) Vậy \(\begin{array}{l}M = - 1 - \frac{1}{2} + \frac{{\sqrt 3 }}{2}i + \frac{1}{{ - 1}} + \frac{1}{{ - \frac{1}{2} + \frac{{\sqrt 3 }}{2}i}} + 5\\M = - 1 - \frac{1}{2} + \frac{{\sqrt 3 }}{2}i + \frac{1}{{ - 1}} - \frac{1}{2} - \frac{{\sqrt 3 }}{2}i + 5\\M = 2.\end{array}\) Chọn B. Câu 48 (VD) Phương pháp: - Đặt \(z = a + bi\) rồi thay vào biểu thức \(\left| {z - 2 + 3i} \right| = \left| {z + 1 - i} \right|\), từ đó rút \(b\) theo \(b\). - Thay vào biểu thức \({\left| z \right|^2} + 2\left( {z + \overline z } \right) = 5\) tìm \(a,\,\,b\). Cách giải: Đặt \(z = a + bi.\) Theo bài ra ta có: \(\begin{array}{l}\,\,\,\,\,\,\,\left| {z - 2 + 3i} \right| = \left| {z + 1 - i} \right|\\ \Leftrightarrow \left| {a + bi - 2 + 3i} \right| = \left| {a + bi + 1 - i} \right|\\ \Leftrightarrow \left| {\left( {a - 2} \right) + \left( {b + 3} \right)i} \right| = \left| {\left( {a + 1} \right) + \left( {b - 1} \right)i} \right|\\ \Leftrightarrow {\left( {a - 2} \right)^2} + {\left( {b + 3} \right)^2} = {\left( {a + 1} \right)^2} + {\left( {b - 1} \right)^2}\\ \Leftrightarrow - 4a + 4 + 6b + 9 = 2a + 1 - 2b + 1\\ \Leftrightarrow 6a - 8b = 11 \Rightarrow b = \frac{{6a - 11}}{8}\end{array}\) Mặt khác ta có: \(\begin{array}{l}\,\,\,\,\,\,\,{\left| z \right|^2} + 2\left( {z + \overline z } \right) = 5\\ \Rightarrow {a^2} + {b^2} + 4a = 5\\ \Rightarrow {a^2} + {\left( {\frac{{6a - 11}}{8}} \right)^2} + 4a - 5 = 0\\ \Leftrightarrow \frac{{25}}{{16}}{a^2} + \frac{{31}}{{16}}a - \frac{{199}}{{64}} = 0\end{array}\) Phương trình trên có 2 nghiệm \(a\) phân biệt. Do đó có 2 số phức \(z\) thỏa mãn yêu cầu bài toán. Chọn C. Câu 49 (VDC) Phương pháp: - Gọi \(A\left( {a;b;c} \right),\) tính tích vô hướng của \(\overrightarrow {OA} .\overrightarrow {MA} .\) - Từ đó suy ra tập hợp các điểm \(A\). Cách giải: Gọi \(A\left( {a;b;c} \right)\) \( \Rightarrow \overrightarrow {OA} = \left( {a;b;c} \right);\)\(\overrightarrow {MA} = \left( {a - 3;b - 1;c - 2} \right)\) Khi đó ta có: \(\begin{array}{l}\overrightarrow {OA} .\overrightarrow {MA} = a\left( {a - 3} \right) + b\left( {b - 1} \right) + c\left( {c - 2} \right)\\ \Leftrightarrow {a^2} + {b^2} + {c^2} - 3a - b - 2c = - 3\,\,\,\left( 1 \right)\end{array}\) Mà \(A \in \left( S \right)\) \(\begin{array}{l} \Rightarrow {\left( {a - 1} \right)^2} + {b^2} + {\left( {c + 2} \right)^2} = 4\\ \Leftrightarrow {a^2} + {b^2} + {c^2} - 2a + 4c = - 1\,\,\,\left( 2 \right)\end{array}\) Trừ vế theo vế của (2) cho (1) ta có: \(a + b + 6c = 2\)\( \Leftrightarrow a + b + 6c - 2 = 0\) Vậy điểm A thuộc mặt phẳng \(x + y + 6z - 2 = 0.\) Chọn A. Câu 50 (VDC) Phương pháp: - Áp dụng phương pháp tích phân từ 0 đến 1 hai vế của \(f\left( {3x} \right) = f\left( x \right) - 2x,\,\,\,\forall x \in \mathbb{R}\). - Sử dụng phương pháp đổi biến số. - Sử dụng tính chất tích phân: \(\int\limits_a^b {f\left( x \right)dx} + \int\limits_b^c {f\left( x \right)dx} = \int\limits_a^c {f\left( x \right)dx} \). Cách giải: Ta có \(f\left( {3x} \right) = f\left( x \right) - 2x\). Lấy tích phân từ 0 đến 1 hai vế ta có: \( \Rightarrow \int\limits_0^1 {f\left( {3x} \right)dx} = \int\limits_0^1 {f\left( x \right)dx - } \int\limits_0^1 {2xdx} \)\(= 5 - 1 = 4\) Đặt \(t = 3x \Rightarrow dt = 3dx\). Đổi cận: \(\left\{ \begin{array}{l}x = 0 \Rightarrow t = 0\\x = 1 \Rightarrow t = 1\end{array} \right.\) \(\begin{array}{l} \Rightarrow \int\limits_0^1 {f\left( {3x} \right)dx} \\ = \frac{1}{3}\int\limits_0^3 {f\left( t \right)dt} = 4\\ \Leftrightarrow \int\limits_0^3 {f\left( t \right)dt} = 12\end{array}\) \( \Rightarrow \int\limits_0^3 {f\left( x \right)dx} = 12\). Vì \(\int\limits_1^3 {f\left( x \right)dx} = \int\limits_1^0 {f\left( x \right)dx} + \int\limits_0^3 {f\left( x \right)dx} \)\( = - 5 + 12 = 7\) Chọn C. loigiaihay.com
|














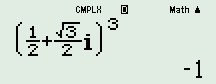






Danh sách bình luận